单调队列 加 二分
雾粉与最小值(简单版)
链接: 牛客
思路
题意是 给定我们数组a让我们完成{x,l,r}询问,判断是否在a中存在子数组满足长度在l,r之间且子数组最小值大于等于x,输出yes 或者 on
一个数组,长度越长,其最小值越小,所以询问只有最小长度是有用的,我们只需要判断是否存在子数组满足最小值大于等于x且长度大于询问的最小长度即可,所以我们的工作就是算出满足大于等于x的子数组的最大长度,显然暴力n^2的时间复杂度铁超时,这时候我们回想算一个子数组的最大长度,不就是找它左边第一个大于他的右边第一个大于他的数的区间嘛,单调队列,两趟O(n)拿下,然后我们获得了每个a[i]的扩展长度,也就是子数组的最小是a[i]的最大长度,这时候我们就像二分大于x的值判断长度是否大于询问的最小值了,可是这时候二分出来的第一个大于x的长度是满足大于等于x的最大长度吗?比如询问的x是5,我们二分出来的是7,7的长度是4,但是后面还有8的长度是9,是不是就错误了,所以我们要把8的长度9加到7的长度上,所以我们还需要给a[i]和他的扩展长度按照a[i]递减排序,然后累计最长长度加到每个a[i]身上,这样我们就确保了二分出来的就是最大长度,这里我们为了方便可以使用map进行二分操作。
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int n, m;
struct node{int x, y;bool operator < (node & tem){if(x != tem.x)return x > tem.x;return y > tem.y;}
};
// 单调栈
int l[N], r[N], len[N];
int main()
{cin >> n;for(int i = 1; i <= n; i ++){cin >> a[i];}stack<int> st;// 找离a[i]最近的小于a[i]的最左位置//6 4 3 6维护一个单调减数列 1 3 2for(int i = 1; i <= n; i ++){while(st.size() && a[st.top()] >= a[i]){st.pop();}if(st.size()) l[i] = st.top()+1;else l[i] = 1;st.push(i);}// 找a[i] 右边最右的大于a[i]的元素stack<int> s;//1 2 3 8 2for(int i = n; i >= 1; i --){while(s.size() && a[s.top()] >= a[i]){s.pop();}if(s.size()) r[i] = s.top()-1;else r[i] = n;s.push(i);}vector<node> c;for(int i = 1; i <= n; i ++){len[i] = r[i] - l[i] + 1;c.push_back({a[i], len[i]});}sort(c.begin(), c.end());int maxlen = 0;map<int, int> cnt;for(int i = 0; i < c.size(); i ++){maxlen = max(maxlen, c[i].y);if(!cnt.count(c[i].x)) cnt[c[i].x] = maxlen;}cin >> m;for(int k = 1; k <= m; k ++){int x, ll, rr; cin >> x >> ll >> rr;auto res = cnt.lower_bound(x);if(res == cnt.end() || (res->second) < ll) cout << "No" << endl;else cout << "Yes" << endl;}return 0;
}
相关文章:

单调队列 加 二分
雾粉与最小值(简单版) 链接: 牛客 思路 题意是 给定我们数组a让我们完成{x,l,r}询问,判断是否在a中存在子数组满足长度在l,r之间且子数组最小值大于等于x,输出yes 或者 on 一个数组,长度越长,其最小值越小ÿ…...

Node.js 和 Vue 的区别的基本知识科普
Node.js和Vue.js在多个方面存在显著的区别。以下是这两者的主要区别,按照清晰的分点表示和归纳: Node.js 服务器端环境: Node.js是一个基于Chrome V8引擎的JavaScript运行环境,它使JavaScript能够在服务器端运行。为JavaScript提供服务器端的环境服务,方便地搭建响应速度…...
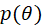
统计信号处理基础 习题解答10-10
题目 在本题中,我们讨论再生PDF。回顾前面 其中分母与无关。如果选择一个,使得它与相乘时,我们得到与相同形式的PDF,那么后验PDF 将有和相同的形式。例10.1的高斯PDF正是这样的一种情况。现在假设在条件下的的PDF是指数形式&…...

【蓝桥杯】C语言常见高级算法
🌸个人主页:Yang-ai-cao 📕系列专栏:蓝桥杯 C语言 🍍博学而日参省乎己,知明而行无过矣 目录 🌸个人主页:Yang-ai-cao 📕系列专栏:蓝桥杯 C语言 &a…...
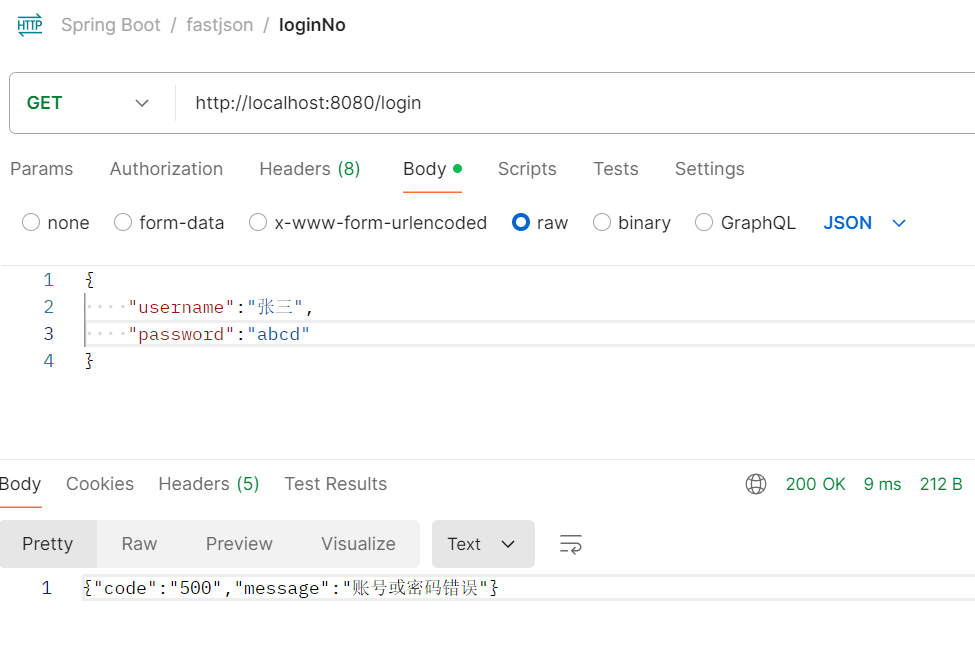
FastJson
目录 FastJson 新建一个SpringBoot项目 pom.xml 一、JavaBean与JSON数据相互转换 LoginController FastJsonApplication启动类 编辑二、FastJson的JSONField注解 Log实体类 TestLog测试类 三、FastJson对JSON数据的增、删、改、查 TestCrud FastJson 1、JSON使用手册…...

Web3设计风格和APP设计风格
Web3设计风格和传统APP设计风格在视觉和交互设计上有一些显著的区别。这些差异主要源于Web3技术和理念的独特性,以及它们在用户体验和界面设计中的具体应用。以下是Web3设计风格与传统APP设计风格的主要区别。北京木奇移动技术有限公司,专业的软件外包开…...
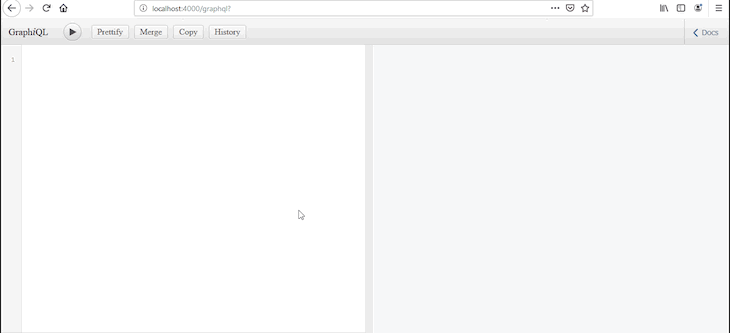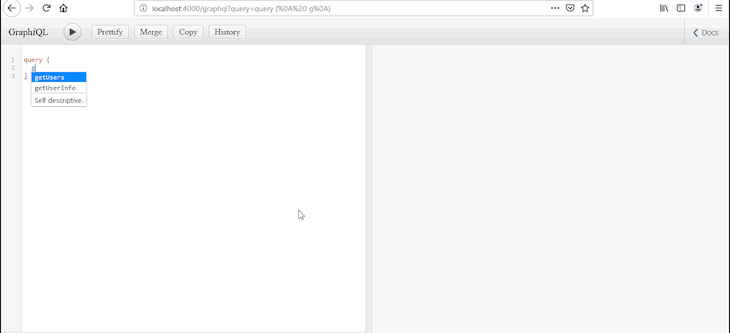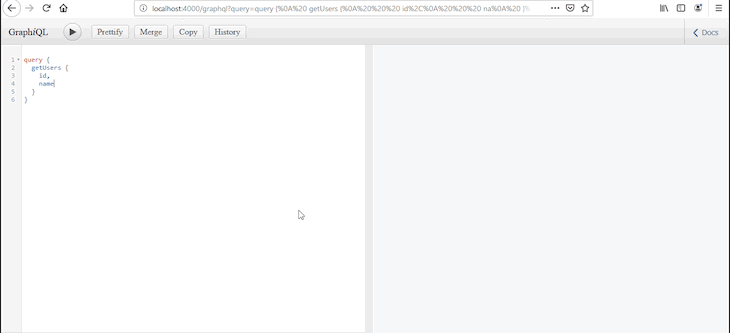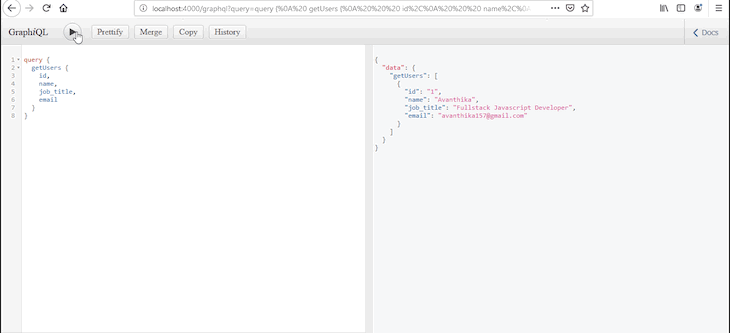
使用React和GraphQL进行CRUD:完整教程与示例
在本教程中,我们将向您展示如何使用GraphQL和React实现简单的端到端CRUD操作。我们将介绍使用React Hooks读取和修改数据的简单示例。我们还将演示如何使用Apollo Client实现身份验证、错误处理、缓存和乐观UI。 什么是React? React是一个用于构建用户…...

matplotlib 动态显示训练过程中的数据和模型的决策边界
文章目录 Github官网文档简介动态显示训练过程中的数据和模型的决策边界安装源码 Github https://github.com/matplotlib/matplotlib 官网 https://matplotlib.org/stable/ 文档 https://matplotlib.org/stable/api/index.html 简介 matplotlib 是 Python 中最常用的绘图…...

【学术小白成长之路】02三方演化博弈(基于复制动态方程)期望与复制动态方程
从本专栏开始,笔者正式研究演化博弈分析,其中涉及到双方演化博弈分析,三方演化博弈分析,复杂网络博弈分析等等。 先阅读了大量相关的博弈分析的文献,总结了现有的研究常用的研究流程,针对每个流程进行拆解。…...

短剧看剧系统投流版系统搭建,前端uni-app
目录 前言: 一、短剧看剧系统常规款短剧系统和投流版的区别? 二、后端体系 1.管理端: 2.代理投流端 三、功能区别 总结: 前言: 23年上半年共上新微短剧481部,相较于2022年全年上新的454部࿰…...

最新的ffmepg.js前端VUE3实现视频、音频裁剪上传功能
package.json "dependencies": {"ffmpeg/ffmpeg": "^0.12.10","ffmpeg/util": "^0.12.1" }vue3组件代码 根据需要更改 <script setup lang"ts"> import { FFmpeg } from ffmpeg/ffmpeg; import { fetchF…...

“Apache Kylin 实战指南:从安装到高级优化的全面教程
Apache Kylin是一个开源的分布式分析引擎,它提供了在Hadoop/Spark之上的SQL查询接口及多维分析(OLAP)能力,支持超大规模数据的亚秒级查询。以下是Kylin的入门教程,帮助您快速上手并使用这个强大的工具。 1. 安装Kylin Apache Kylin的安装是一个关键步骤,它要求您具备一…...

【iOS】内存泄漏检查及原因分析
目录 为什么要检测内存泄漏?什么是内存泄漏?内存泄漏排查方法1. 使用Zombie Objects2. 静态分析3. 动态分析方法定位修改Leaks界面分析Call Tree的四个选项: 内存泄漏原因分析1. Leaked Memory:应用程序未引用的、不能再次使用或释…...

“深入探讨Java中的对象拷贝:浅拷贝与深拷贝的差异与应用“
前言:在Java编程中,深拷贝(Deep Copy)与浅拷贝(Shallow Copy)是两个非常重要的概念。它们涉及到对象在内存中的复制方式,对于理解对象的引用、内存管理以及数据安全都至关重要。 ✨✨✨这里是秋…...

Docker 进入指定容器内部(以Mysql为例)
文章目录 一、启动容器二、查看容器是否启动三、进入容器内部 一、启动容器 这个就不多说了 直接docker run… 二、查看容器是否启动 查看正在运行的容器 docker ps查看所有的容器 docker ps -a结果如下图所示: 三、进入容器内部 通过CONTAINER ID进入到容器…...

计算机网络-数制转换与子网划分
目录 一、了解数制 1、计算机的数制 2、二进制 3、八进制 4、十进制 5、十六进制 二、数制转换 1、二进制转十进制 2、八进制转十进制 3、十六进制转十进制 4、十进制转二进制 5、十进制转八进制 6、十进制转十六进制 三、子网划分 1、IP地址定义 2、IP的两种协…...
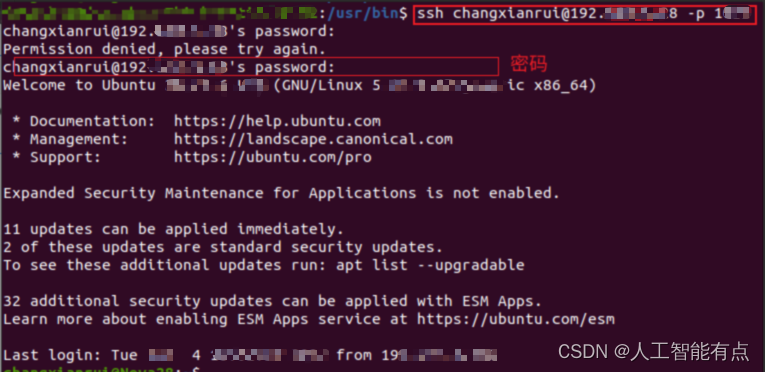
【ssh命令】ssh登录远程服务器
命令格式:ssh 用户名主机IP # 使用非默认端口: -p 端口号 ssh changxianrui192.168.100.100 -p 1022 # 使用默认端口 22 ssh changxianrui192.168.100.100 然后输入密码,就可以登录进去了。...
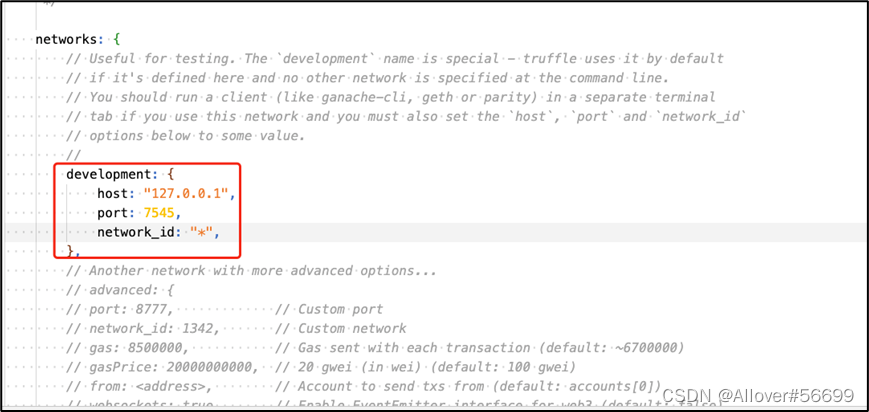
【区块链】truffle测试
配置区块链网络 启动Ganache软件 使用VScode打开项目的wordspace 配置对外访问的RPC接口为7545,配置项目的truffle-config.js实现与新建Workspace的连接。 创建项目 创建一个新的目录 mkdir MetaCoin cd MetaCoin下载metacoin盒子 truffle unbox metacoincontra…...

【AIGC调研系列】chatTTS与GPT-SoVITS的对比优劣势
ChatTTS和GPT-SoVITS都是在文本转语音(TTS)领域的重要开源项目,但它们各自有不同的优势和劣势。 ChatTTS 优点: 多语言支持:ChatTTS支持中英文,并且能够生成高质量、自然流畅的对话语音[4][10][13]。细粒…...

LLVM Cpu0 新后端10
想好好熟悉一下llvm开发一个新后端都要干什么,于是参考了老师的系列文章: LLVM 后端实践笔记 代码在这里(还没来得及准备,先用网盘暂存一下): 链接: https://pan.baidu.com/s/1yLAtXs9XwtyEzYSlDCSlqw?…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
