transformer - 注意力机制

Transformer 的注意力机制
Transformer 是一种用于自然语言处理任务的模型架构,依赖于注意力机制来实现高效的序列建模。注意力机制允许模型在处理一个位置的表示时,考虑输入序列中所有其他位置的信息,而不仅仅是前面的几个位置。这种机制能够捕捉远距离的依赖关系,是 Transformer 的核心组件。
注意力机制的核心组件
在 Transformer 中,注意力机制的核心组件包括查询(Query,Q)、键(Key,K)和值(Value,V)。这些组件的具体作用和生成过程如下:
- 查询(Query,Q): 表示需要查找的信息。
- 键(Key,K): 表示可以提供的信息。
- 值(Value,V): 表示每个位置的实际信息或特征。
这些组件通过以下步骤实现注意力机制:
1. 输入嵌入和线性变换
原理解释: 输入序列首先通过嵌入层转化为嵌入向量,然后通过线性变换生成查询、键和值向量。假设输入序列为 X X X,线性变换生成 Q、K 和 V 的公式如下:
Q = X W Q , K = X W K , V = X W V Q = XW^Q, \quad K = XW^K, \quad V = XW^V Q=XWQ,K=XWK,V=XWV
生活中的例子: 想象你在图书馆寻找书籍。每本书都有其特定的主题标签(嵌入向量)。你通过查询标签(Q)寻找与你想读的书(K)匹配的标签,然后提取相应书籍的内容(V)。
目的: 通过线性变换生成查询、键和值向量,确保模型能够在统一的特征空间中进行相似度计算。
原因解释: 将输入转化为统一的特征表示后,模型能够更有效地计算相似度,并进行后续的注意力计算。
2. 计算点积注意力
原理解释: 点积注意力(Dot-Product Attention)的计算包括以下几个步骤:
-
计算查询和键的点积: 计算查询向量 Q Q Q 和键向量 K K K 的点积,得到相似度矩阵。
Q K T QK^T QKT
-
缩放点积: 将点积结果除以键向量维度的平方根 d k \sqrt{d_k} dk 进行缩放。
Q K T d k \frac{QK^T}{\sqrt{d_k}} dkQKT
-
应用 Softmax 函数: 对缩放后的点积结果应用 softmax 函数,得到注意力权重。
A = softmax ( Q K T d k ) A = \text{softmax}\left( \frac{QK^T}{\sqrt{d_k}} \right) A=softmax(dkQKT)
-
加权求和值向量: 使用注意力权重对值向量 V V V 进行加权求和,得到最终的注意力输出。
Z = A V Z = AV Z=AV
生活中的例子: 你在图书馆用一个关键词(Q)搜索书籍。图书馆系统会根据每本书的主题标签(K)计算与关键词的相似度(点积),然后按照相似度高低(softmax)推荐书籍,并根据这些推荐给你提取书籍的内容(V)。
目的: 计算每个查询与键的相似度,分配注意力权重,并根据这些权重对值进行加权求和,得到最终的注意力输出。
原因解释: 通过计算相似度,模型能够识别输入序列中哪些部分相关,从而根据相关性分配注意力。缩放操作确保数值稳定,softmax 函数将相似度转化为概率分布,加权求和则整合了相关信息。
缩放点积的数学推导
为什么使用 d k \sqrt{d_k} dk 进行缩放?这是因为点积的期望和方差。假设 Q Q Q 和 K K K 的每个元素是零均值单位方差的随机变量:
- 点积的期望为0。
- 点积的方差为 d k d_k dk。
通过缩放,使得点积的期望和方差标准化,防止数值过大导致梯度消失和数值不稳定。
生活中的例子: 想象你在图书馆搜索书籍时,系统会根据标签(K)的数量调整搜索结果的相似度计算。例如,如果标签很多,系统会将相似度分数进行缩放,避免过大的数值影响推荐。
目的: 缩放点积结果,确保数值稳定,避免梯度消失和数值不稳定问题。
原因解释: 点积的方差随着维度增加而变大,缩放操作将其标准化,确保计算的数值范围合理,从而提高模型训练的稳定性和效果。
3. 多头注意力机制
原理解释: 为了捕捉输入序列中的不同特征,Transformer 使用多头注意力机制(Multi-Head Attention)。具体步骤如下:
-
线性变换生成多个头的 Q、K 和 V: 对输入进行多次线性变换,生成多个头的查询、键和值。
-
独立计算每个头的注意力: 对每个头独立计算注意力。
-
拼接多个头的输出: 将所有头的输出拼接在一起。
-
线性变换融合多个头的输出: 对拼接后的输出进行线性变换,得到最终输出。
生活中的例子: 想象你在图书馆用不同的关键词(多个头)搜索书籍。每个关键词会得到一组推荐书籍(每个头的输出),然后你将所有推荐结果综合考虑,得到最终的书籍列表(拼接和线性变换)。
目的: 捕捉输入序列中的多种特征,增强模型的表达能力。
原因解释: 不同的头能够关注输入序列中的不同部分,通过多头注意力机制,模型能够更全面地理解输入序列中的信息。
4. 位置编码
原理解释: 由于 Transformer 不包含递归或卷积结构,因此需要引入位置编码(Positional Encoding)来保留输入序列中元素的位置信息。位置编码是添加到输入嵌入中的固定或可学习的向量。
常用的正弦和余弦位置编码公式如下:
P E ( p o s , 2 i ) = sin ( p o s 1000 0 2 i / d model ) PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) PE(pos,2i)=sin(100002i/dmodelpos)
P E ( p o s , 2 i + 1 ) = cos ( p o s 1000 0 2 i / d model ) PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) PE(pos,2i+1)=cos(100002i/dmodelpos)
生活中的例子: 想象你在图书馆借书时,图书馆会记录每本书的位置(位置编码),即使书籍内容相同,位置不同也会影响你找到书的效率。
目的: 保留输入序列中元素的位置信息,使模型能够捕捉顺序信息。
原因解释: 位置信息对于语言理解非常重要,通过位置编码,模型能够更好地理解序列中元素的相对位置和顺序。
5. 残差连接和层归一化
原理解释: 每个注意力层和前馈神经网络层后面都有残差连接(Residual Connection)和层归一化(Layer Normalization),以确保梯度流动更顺畅,并加速模型训练。
生活中的例子: 想象你在图书馆阅读书籍时,有一个记录你阅读进度的系统(残差连接),确保你不会丢失之前的阅读进度。同时,图书馆会定期整理和归类书籍(层归一化),确保书籍的排列整齐有序。
目的: 确保梯度流动更顺畅,加速模型训练,保持输入和输出的数值稳定。
原因解释: 残差连接能够避免梯度消失问题,层归一化则确保输入和输出的数值范围一致,增强模型的训练效果。
6. 前馈神经网络
原理解释: 注意力机制的输出通过前馈神经网络(Feedforward Neural Network, FFN),每个位置独立地通过相同的网络。FFN 包括两个线性变换和一个激活函数:
FFN ( x ) = max ( 0 , x W 1 + b 1 ) W 2 + b 2 \text{FFN}(x) = \max(0, xW_1 + b_1)W_2 + b_2 FFN(x)=max(0,xW1+b1)W2+b2
生活中的例子: 想象你在图书馆选择了几本书(注意力输出),然后你决定逐本阅读,并将每本书的内容进行总结和理解(前馈神经网络处理)。
目的: 对注意力输出进行进一步的特
征提取和处理。
原因解释: 前馈神经网络能够对每个位置的特征进行深度处理,提取更高层次的表示。
7. Transformer 编码器和解码器
原理解释: Transformer 包括编码器和解码器两个部分:
- 编码器(Encoder): 由多个相同的层组成,每层包括多头注意力机制和前馈神经网络。
- 解码器(Decoder): 与编码器类似,但每层包括额外的一个用于处理编码器输出的多头注意力层。
编码器和解码器的交互通过注意力机制,解码器中的多头注意力机制利用编码器的输出来生成新的序列。
生活中的例子: 想象你在图书馆借书(编码器),你阅读这些书并记下笔记(解码器),然后用这些笔记写一篇文章(生成新的序列)。
目的: 实现序列到序列的任务,如机器翻译和文本生成。
原因解释: 编码器提取输入序列的特征,解码器根据这些特征生成新的序列,完成语言理解和生成任务。
结合具体实例
假设我们有一个句子 “I love NLP”,输入嵌入如下:
X = ( 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 ) X = \begin{pmatrix} 0.1 & 0.2 & 0.3 \\ 0.4 & 0.5 & 0.6 \\ 0.7 & 0.8 & 0.9 \end{pmatrix} X= 0.10.40.70.20.50.80.30.60.9
通过线性变换生成 Q、K 和 V:
Q = X W Q , K = X W K , V = X W V Q = XW^Q, \quad K = XW^K, \quad V = XW^V Q=XWQ,K=XWK,V=XWV
假设 W Q W^Q WQ、 W K W^K WK 和 W V W^V WV 是:
W Q = ( 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 ) , W K = ( 0.1 0.3 0.5 0.2 0.4 0.6 0.3 0.5 0.7 ) , W V = ( 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 ) W^Q = \begin{pmatrix} 0.1 & 0.2 & 0.3 \\ 0.4 & 0.5 & 0.6 \\ 0.7 & 0.8 & 0.9 \end{pmatrix}, \quad W^K = \begin{pmatrix} 0.1 & 0.3 & 0.5 \\ 0.2 & 0.4 & 0.6 \\ 0.3 & 0.5 & 0.7 \end{pmatrix}, \quad W^V = \begin{pmatrix} 0.1 & 0.2 & 0.3 \\ 0.4 & 0.5 & 0.6 \\ 0.7 & 0.8 & 0.9 \end{pmatrix} WQ= 0.10.40.70.20.50.80.30.60.9 ,WK= 0.10.20.30.30.40.50.50.60.7 ,WV= 0.10.40.70.20.50.80.30.60.9
计算结果:
Q = ( 0.14 0.32 0.5 0.32 0.77 1.22 0.5 1.22 1.94 ) , K = ( 0.26 0.44 0.62 0.62 1.07 1.52 0.98 1.7 2.42 ) , V = ( 0.14 0.32 0.5 0.32 0.77 1.22 0.5 1.22 1.94 ) Q = \begin{pmatrix} 0.14 & 0.32 & 0.5 \\ 0.32 & 0.77 & 1.22 \\ 0.5 & 1.22 & 1.94 \end{pmatrix}, \quad K = \begin{pmatrix} 0.26 & 0.44 & 0.62 \\ 0.62 & 1.07 & 1.52 \\ 0.98 & 1.7 & 2.42 \end{pmatrix}, \quad V = \begin{pmatrix} 0.14 & 0.32 & 0.5 \\ 0.32 & 0.77 & 1.22 \\ 0.5 & 1.22 & 1.94 \end{pmatrix} Q= 0.140.320.50.320.771.220.51.221.94 ,K= 0.260.620.980.441.071.70.621.522.42 ,V= 0.140.320.50.320.771.220.51.221.94
通过点积和 softmax 计算得到注意力权重矩阵 A A A:
A = ( 0.2 0.3 0.5 0.1 0.7 0.2 0.4 0.4 0.2 ) A = \begin{pmatrix} 0.2 & 0.3 & 0.5 \\ 0.1 & 0.7 & 0.2 \\ 0.4 & 0.4 & 0.2 \end{pmatrix} A= 0.20.10.40.30.70.40.50.20.2
将注意力权重应用于值向量,得到最终输出矩阵 Z Z Z:
Z = A V Z = AV Z=AV
Z = ( 0.2 0.3 0.5 0.1 0.7 0.2 0.4 0.4 0.2 ) ( 0.14 0.32 0.5 0.32 0.77 1.22 0.5 1.22 1.94 ) = ( 0.342 0.81 1.278 0.21 0.658 1.106 0.256 0.612 0.968 ) Z = \begin{pmatrix} 0.2 & 0.3 & 0.5 \\ 0.1 & 0.7 & 0.2 \\ 0.4 & 0.4 & 0.2 \end{pmatrix} \begin{pmatrix} 0.14 & 0.32 & 0.5 \\ 0.32 & 0.77 & 1.22 \\ 0.5 & 1.22 & 1.94 \end{pmatrix} = \begin{pmatrix} 0.342 & 0.81 & 1.278 \\ 0.21 & 0.658 & 1.106 \\ 0.256 & 0.612 & 0.968 \end{pmatrix} Z= 0.20.10.40.30.70.40.50.20.2 0.140.320.50.320.771.220.51.221.94 = 0.3420.210.2560.810.6580.6121.2781.1060.968
总结
Transformer 中的注意力机制通过查询(Q)、键(K)和值(V)捕捉输入序列中元素之间的相关性,利用多头注意力机制增强模型的表达能力。通过缩放点积、应用 softmax、加权求和值向量,模型能够有效地调整输入序列中的信息权重。位置编码确保了位置信息的保留,残差连接和层归一化加速了训练,前馈神经网络进一步处理了注意力输出。编码器和解码器的结合使得 Transformer 能够高效地进行序列到序列的任务,如机器翻译和文本生成。
相关文章:

transformer - 注意力机制
Transformer 的注意力机制 Transformer 是一种用于自然语言处理任务的模型架构,依赖于注意力机制来实现高效的序列建模。注意力机制允许模型在处理一个位置的表示时,考虑输入序列中所有其他位置的信息,而不仅仅是前面的几个位置。这种机制能…...

三端植物大战僵尸杂交版来了
Hi,好久不见,最近植物大战僵尸杂交版蛮火的 那今天苏音整理给大家三端的植物大战僵尸杂交版包括【苹果端、电脑端、安卓端】 想要下载的直接划到最下方即可下载。 植物大战僵尸,作为一款古老的单机游戏,近期随着B站一位UP主潜艇…...
和np.vstack()函数解释)
np.hstack()和np.vstack()函数解释
np.hstack()和np.vstack()函数解释 文章目录 1,np.hstack()1.1,代码1.2,结果 2,np.vstack()2.1,代码2.2,结果 3,np.hstack()和np.vstack()3.1,代码3.2,结果 1,…...

【Linux】进程5——进程优先级
1.进程优先级 1.1.什么是进程优先级 cpu资源分配的先后顺序,就是指进程的优先权(priority)。优先权高的进程有优先执行权利。配置进程优先权对多任务环境的linux很有用,可以改善系统性能。还可以把进程运行到指定的CPU上&#x…...

CNN简介与实现
CNN简介与实现 导语整体结构卷积层卷积填充步幅三维卷积立体化批处理 实现 池化层特点实现 CNN实现可视化总结参考文献 导语 CNN全称卷积神经网络,可谓声名远扬,被用于生活中的各个领域,也是最好理解的神经网络结构之一。 整体结构 相较于…...

【AI大模型】Transformers大模型库(五):AutoModel、Model Head及查看模型结构
目录 一、引言 二、自动模型类(AutoModel) 2.1 概述 2.2 Model Head(模型头) 2.3 代码示例 三、总结 一、引言 这里的Transformers指的是huggingface开发的大模型库,为huggingface上数以万计的预…...
,新增表字段,删除表字段,修改存储格式)
Hadoop yixing(移行),新增表字段,删除表字段,修改存储格式
Hadoop yixing(移行),新增表字段,删除表字段,修改存储格式 一、hadoop中修改存储格式,比如从 textfile 转化为 orc 格式,表中的数据的组织形式要重新改变,就要将重新创建新格式的表将原来的数据按照新的格…...
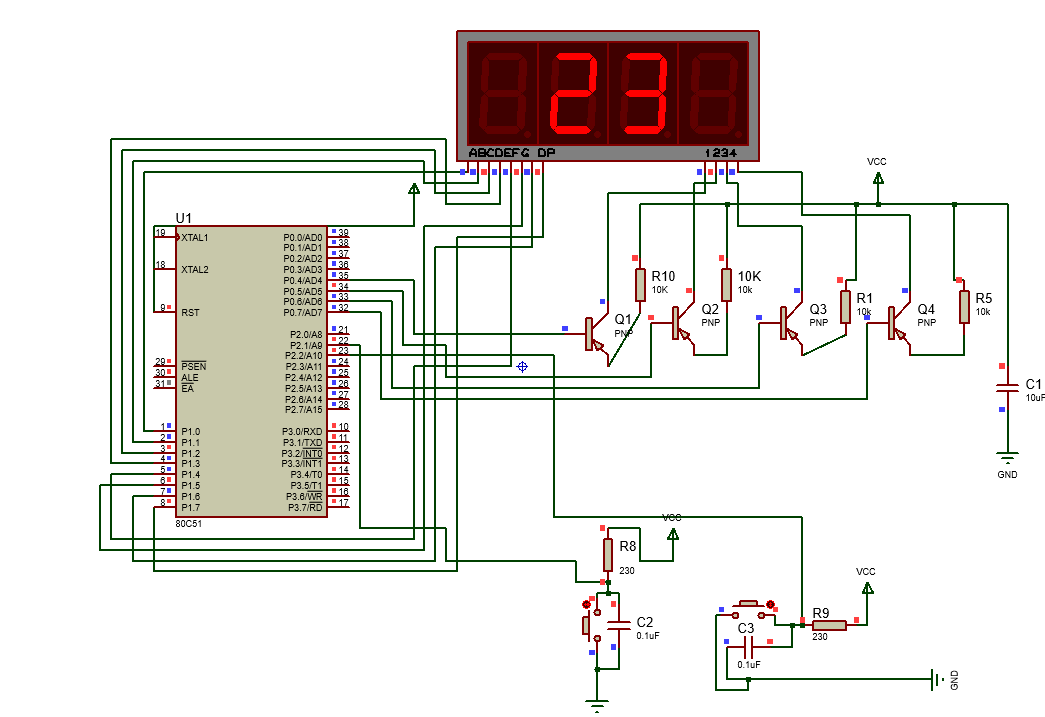
使用汇编和proteus实现仿真数码管显示电路
proteus介绍: proteus是一个十分便捷的用于电路仿真的软件,可以用于实现电路的设计、仿真、调试等。并且可以在对应的代码编辑区域,使用代码实现电路功能的仿真。 汇编语言介绍: 百度百科介绍如下: 汇编语言是培养…...
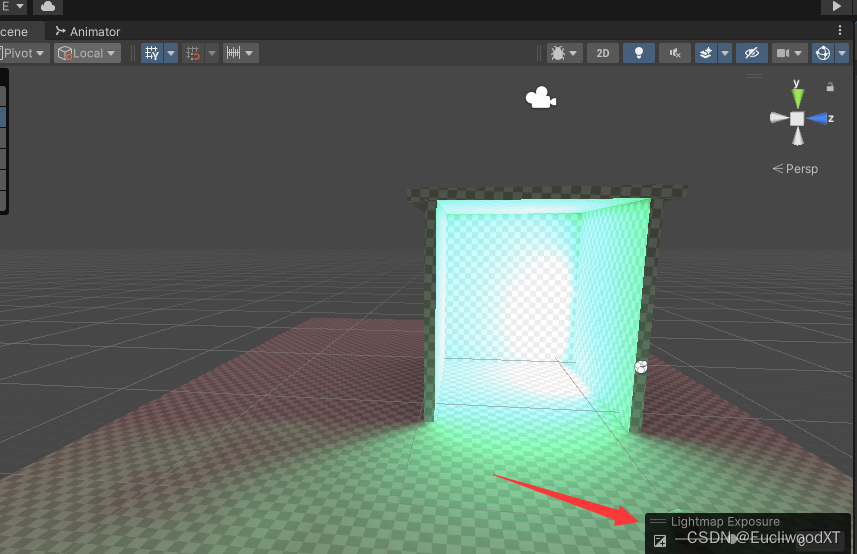
【Unity】官方文档学习-光照系统
目录 1 前言 2 光照介绍 2.1 直接光与间接光 2.2 实时光照与烘焙光照 2.3 全局光照 3 光源 3.1 Directional Light 3.1.1 Color 3.1.2 Mode 3.1.3 Intensity 3.1.4 Indirect Multiplier 3.1.5 Shadow Type 3.1.6 Baked Shadow Angle 3.1.7 Realtime Shadows 3.1…...

1731. 每位经理的下属员工数量
1731. 每位经理的下属员工数量 题目链接:1731. 每位经理的下属员工数量 代码如下: # Write your MySQL query statement below select a.employee_id as employee_id,a.name as name,count(b.employee_id) as reports_count,round(avg(b.age),0) as av…...

特征筛选LASSO回归封装好的代码、数据集和结果
Gitee仓库地址:特征筛选LASSO回归封装好的代码、数据集和结果 README LassoFeatureSelector_main 这个是主函数文件,在实例化LassoFeatureSelector类时,需要传入下面这些参数: input_train_data_path:输入训练集的路…...

Autosar 通讯栈配置-手动配置PDU及Signal-基于ETAS软件
文章目录 前言System配置ISignalSystem SignalPduFrameISignal到System Signal的mapSystem Signal到Pdu的mapPdu到Frame的mapSignal配置Can配置CanHwFilterEcuC配置PduR配置CanIf配置CanIfInitCfgCanIfRxPduCfgCom配置ComIPduComISignalSWC配置Data mappingRTE接口Com配置补充总…...

Web前端工资调整:深入剖析与全面解读
Web前端工资调整:深入剖析与全面解读 在快速发展的互联网行业中,Web前端技术日新月异,而与之紧密相关的工资调整也成为了业内热议的话题。本文将从四个方面、五个方面、六个方面和七个方面,深入剖析Web前端工资调整的原因、趋势、…...

cesium已知两个点 写一个简单具有动画尾迹效果的抛物线
// 定义起点和终点的经纬度和高度 var start { longitude: 111.09683723811149, latitude: 38.92112250636146, elevation: 603.5831692856873 }; var end { longitude: 111.09769465526689, latitude: 38.92815375977821, elevation: 627.0132157062261 }; // 生成更多的中…...
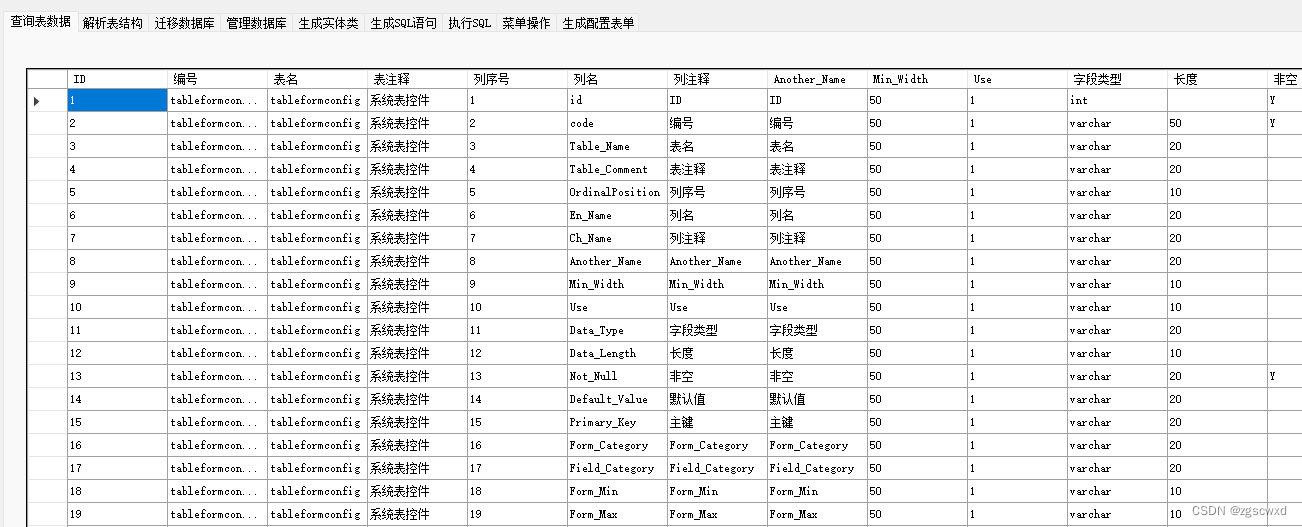
C#中使用Mysql批量新增数据 MySqlBulkCopy
在C#中使用MySqlBulkCopy类来批量复制数据到MySQL数据库,首先需要确保你的项目中已经引用了MySQL Connector。以下是使用MySqlBulkCopy的基本步骤: 1.安装MySQL Connector。 可以通过NuGet安装MySQL Connector: 2.在代码中引用必要的命名空间…...

ARM-V9 RME(Realm Management Extension)系统架构之系统安全能力的架构差异
安全之安全(security)博客目录导读 RME系统中的应用处理单元(PE)之间的架构差异可能会带来潜在的安全风险并增加管理软件的复杂性。例如,通过在ID_AA64MMFR0_EL1.PARange中为每个PE设置不同的值来支持不同的物理范围,可能会妨碍内…...

Ansible——stat模块
目录 参数总结 返回值 基础语法 常见的命令行示例 示例1:检查文件是否存在 示例2:获取文件详细信息 示例3:检查目录是否存在 示例4:获取文件的 MD5 校验和 示例5:获取文件的 MIME 类型 高级使用 示例6&…...

第二十节:带你梳理Vue2:Vue子组件向父组件传参(事件传参)
1. 自定义事件 除了可以处理原生的DOM事件, v-on指令也可以处理组件内部触发的自定义的事件,调用this.$emit()函数就可以触发一个自定义事件 $emit() 触发事件函数接受一个自定义事件的事件名以及其他任何给事件函数传递的参数. 然后就可以在组件上使用v-on来绑定这个自定义事…...

华为od-C卷100分题目 - 10寻找最富裕的小家庭
华为od-C卷100分题目 - 10寻找最富裕的小家庭 题目描述 在一棵树中,每个节点代表一个家庭成员,节点的数字表示其个人的财富值,一个节点及其直接相连的子节点被定义为一个小家庭。 现给你一棵树,请计算出最富裕的小家庭的财富和。…...

本地部署AI大模型 —— Ollama文档中文翻译
写在前面 来自Ollama GitHub项目的README.md 文档。文档中涉及的其它文档未翻译,但是对于本地部署大模型而言足够了。 Ollama 开始使用大模型。 macOS Download Windows 预览版 Download Linux curl -fsSL https://ollama.com/install.sh | sh手动安装说明 …...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...
