C++笔试强训day42

目录

1.最大差值

2.兑换零钱

3.小红的子串

---

1.最大差值

链接https://www.nowcoder.com/practice/a01abbdc52ba4d5f8777fb5dae91b204?tpId=182&tqId=34396&rp=1&ru=/exam/company&qru=/exam/company&sourceUrl=%2Fexam%2Fcompany&difficulty=2&judgeStatus=undefined&tags=&title=

因为b >= a，所以可以在遍历数组的时候更新所遍历到的最小值以及返回值即可

class Solution {public:int getDis(vector<int>& A, int n) {int ret = -0x3f3f3f3f;int l = 0, r = l + 1;while (r < n) {ret = max(A[r] - A[l], ret);if (A[r] < A[l]) {l = r;}r++;}return ret < 0 ? 0 : ret;}
};

2.兑换零钱

链接https://www.nowcoder.com/practice/67b93e5d5b85442eb950b89c8b77bc72?tpId=230&tqId=40432&ru=/exam/oj

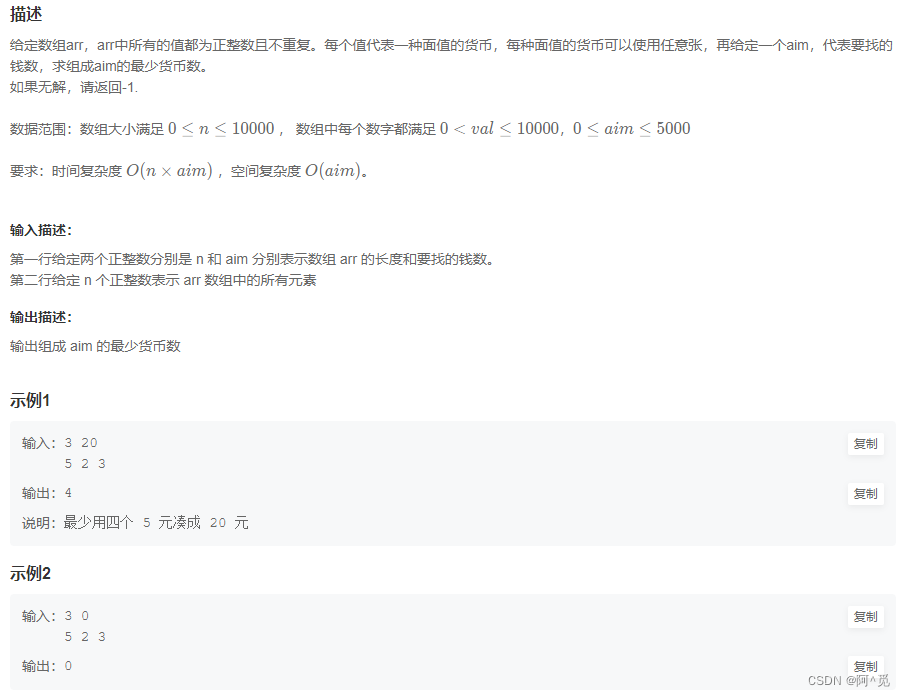
每个值代表一种面值的货币，每种面值的货币可以使用任意张

根据题意，可以分析出这是一道完全背包类型的题目：

直接分析状态转移方程和注意初始化的细节即可

#include <cstring>
#include <iostream>
using namespace std;
const int N = 10010;int w[N];
int dp[5010];
int n, aim;
int main()
{cin >> n >> aim;for(int i = 1; i <= n; ++i)cin >> w[i];memset(dp, 0x3f3f3f3f, sizeof dp);dp[0] = 0;for(int i = 1; i <= n; ++i){for(int j = w[i]; j <= aim; ++j){dp[j] = min(dp[j], dp[j - w[i]] + 1);}}cout << (dp[aim] == 0x3f3f3f3f ? -1 : dp[aim]) << endl;return 0;
}

3.小红的子串

链接https://ac.nowcoder.com/acm/problem/260770

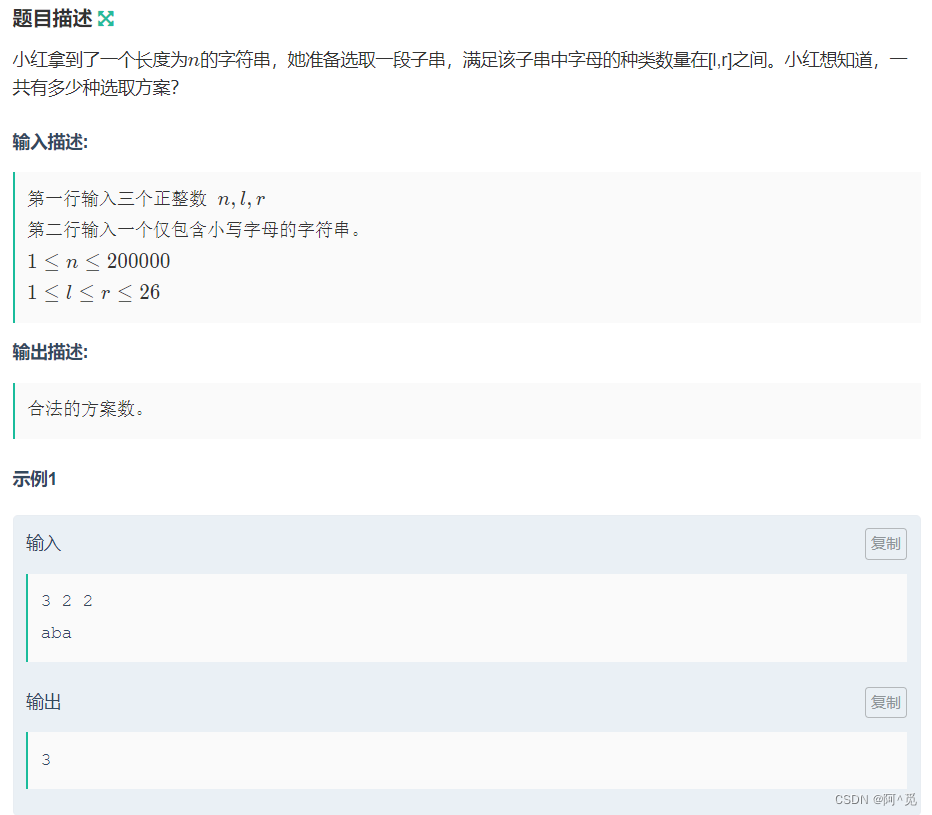
若种类的范围为 【1，x】的话，则满足条件的数组区间内方案数则为 right - left + 1，因此可以将种类范围想办法变为【1，x】，最后用【1，r】 - 【1，l】即可

滑动窗口遍历数组：（数据范围过大，注意开long long）

#include <iostream>
#include <cstring>
#define int long long
using namespace std;int n, l, r;
char s[200010];int find(int x)
{if(x == 0)return 0;int cnt[26] = { 0 };int kind = 0, ret = 0;int L = 1, R = 1;while(R <= n){if(cnt[s[R] - 'a']++ == 0)kind++;while(kind > x){if(cnt[s[L++] - 'a']-- == 1)kind--;}ret += R - L + 1;R++;}return ret;
}signed main()
{cin >> n >> l >> r;for(int i = 1; i <= n; ++i)cin >> s[i];cout << find(r) - find(l - 1) << endl;return 0;
}