做互联网自媒体创业的月薪收入真的能过万吗?
搞自媒体创业有前途吗?收入月薪过万是真的吗?
自媒体创业是一种新兴的创业方法,它的远景十分广阔。自媒体创业能够让人们在自己的兴趣爱好和专业范畴上发挥自己的才能,一起也能够获得不错的收入。可是,月薪过万并不是每个自媒体人都能完成的,需求具有必定的条件和技术。

首先,自媒体创业需求有必定的专业知识和技术。假如你想在某个范畴做自媒体,就需求对这个范畴有深入的了解和研究。
比方,假如你想做美食自媒体,就需求对食材、烹饪技巧、口味等方面有必定的了解和经验。只要具有了这些专业知识和技术,才能够在自媒体范畴中锋芒毕露。
其次,自媒体创业需求有必定的创新才能和构思。在自媒体范畴中,内容构思是十分重要的。假如你的内容没有构思和亮点,很难招引到读者的关注和喜爱。
因而,自媒体人需求不断地创新和提高自己的构思才能,才能够在剧烈的竞赛中锋芒毕露。
再次,自媒体创业需求有必定的市场营销才能。在自媒体范畴中,内容的质量和构思是十分重要的,可是,假如没有好的市场营销策略,很难让更多的人知道你的存在。
因而,自媒体人需求具有必定的市场营销才能,能够通过各种渠道和方法宣传自己的内容,招引更多的读者和粉丝。
最后,月薪过万并不是每个自媒体人都能完成的。尽管自媒体创业能够获得不错的收入,可是,要想月薪过万,需求具有必定的条件和技术。
比方,你需求有大量的粉丝和读者,需求有稳定的广告和赞助收入,需求有必定的商业合作和推广收入等等。只要具有了这些条件和技术,才能够完成月薪过万的方针。
总之,自媒体创业是一种十分有出路的创业方法,能够让人们在自己的兴趣爱好和专业范畴上发挥自己的才能,一起也能够获得不错的收入。
可是,要想在自媒体范畴中锋芒毕露,需求具有必定的专业知识和技术,需求有创新才能和构思,需求有市场营销才能,一起也需求有耐心和意志。只要具有了这些条件和技术,才能够在自媒体范畴中取得成功。
相关文章:

做互联网自媒体创业的月薪收入真的能过万吗?
搞自媒体创业有前途吗?收入月薪过万是真的吗? 自媒体创业是一种新兴的创业方法,它的远景十分广阔。自媒体创业能够让人们在自己的兴趣爱好和专业范畴上发挥自己的才能,一起也能够获得不错的收入。可是,月薪过万并不是…...
 污点(Taint)、容忍介绍、示例)
Kubernetes (k8s) 污点(Taint)、容忍介绍、示例
Kubernetes (k8s) 污点(Taint) 是一种机制,用于标记一个节点(Node)不可被调度的状态。它可以将一个污点标记添加到节点上,以防止 Pod 被调度到该节点上。污点可以用于实现各种策略,例如分离故障…...

多团队协作构建可观测性
实施 SRE 工程,守护系统的可靠性是一个⻓期的工作,需要开发、测试、运维以及 SRE 整个团队的努力。而可观测性平台天生就是为 SRE 工程服务的,它致力于实现 SLO 目标。建立可观测性不仅仅是运维团队的事情,更是整个开发、测试以及…...

100种思维模型之认知资源思维模型-030
我们常说,一个人永远也赚不到自己认知以外的钱,这话的确很有道理,被无数人所推崇。 由此,不难看出,认知在我们的生活起着多么关键的作用。 你的认知层次越高,范围越广,就意味着你这个人所处的阶…...
c/cpp - 多线程/进程 基础
c/cpp - 多线程/进程 基础1. 概念1.1 程序1.2 任务1.3 多任务1.4 进程1.5 线程1.5 线程/进程应用程序/系统资源并发/并行/同步/异步1. 概念 1.1 程序 代码、指令,静态的 1.2 任务 具体要做的实景,可以是基于进程、或基于线程 1.3 多任务 例如࿱…...

第55章 头像图片的前端渲染显示
1 WebApi.Controllers.CustomerController.GetCustomerByToken /// <param name"token">1个指定的令牌字符串。</param> /// <summary> /// 【通过令牌获取用户-无需权限】 /// </summary> /// <remarks> /// 摘要: /// …...

vue2 使用 cesium 【第二篇-相机视角移动+添加模型】
vue2 使用 cesium 【第二篇-相机视角移动添加模型】 搞了一阵子 cesium,小白入门,这东西很牛逼,但是感觉这东西好费劲啊!网上资料不多,每个人的用法又不一样,操作起来真的是绝绝子。之前写了一篇 vue2 使用…...

C/C++ 操作ini文件(SinpleIni 跨平台库)
最近在学习时,发现自己还不会操作ini文件,想着以前工作时接触到的项目或多或少都要用到ini文件去保存初始化程序的数据;所以赶紧去网上搜索以下C/C操作ini文件都有些什么库可以玩玩;搜索到有: 1. inih:这是…...
Report报告详解)
Cadence Allegro 导出Design Rules Check(DRC)Report报告详解
⏪《上一篇》 🏡《上级目录》 ⏩《下一篇》 目录 1,概述2,Design Rules Check(DRC)Report作用3,Design Rules Check(DRC)Report示例4,Design Rules Check(DRC)Report导出方法4.1,方法14.2,方法2B站关注“硬小...
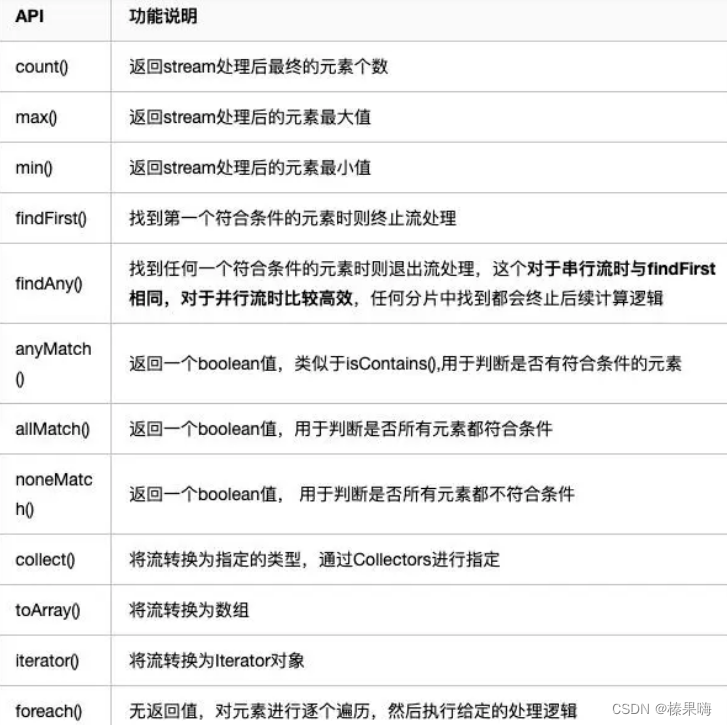
Java的stream流
Java 8中引入的新特性,stream流通过与Lambda表达式结合,采用函数式编程,简化数组、集合操作,提高效率。 我们操作一个集合,就把他看作一个流,整个流依次执行,(可以类比为一个管道&a…...

Mybatis_相关配置解析和ResultMap
目录配置解析核心配置文件mybatis-config.xml 系统核心配置文件environments元素子元素节点:environmentmappers元素Mapper文件Properties优化typeAliases优化その他生命周期和作用域(Scope)方法作用域应用作用域方法作用域ResultMap提出问题…...

Python量化入门:利用中长期RSI寻找趋势拐点,抓大放小,蹲一个大机会!
一、RSI的原理 1. RSI简介 股票的涨跌说白了就是多空博弈造成的,多方力量更强则股票价格上涨,空方力量更强则股票价格下跌。那么我们如何来衡量股票的多空力量强弱呢? 上个世纪70年代,威尔斯威尔得发表了相对强弱指标,即我们常说的RSI(Relative Strength Index),RSI…...

案例14-代码结构逻辑混乱,页面设计不美观
目录 目录 一:背景介绍 二:思路&方案 三:过程 问题1:代码可读性差,代码结构混乱 问题2: 代码逻辑混乱,缺乏封装的意识 问题3:美观问题:问题和图标没有对应上 四…...

弱监督参考图像分割:Learning From Box Annotations for Referring Image Segmentation论文阅读笔记
弱监督参考图像分割:Learning From Box Annotations for Referring Image Segmentation论文阅读笔记一、Abstract二、引言三、相关工作A、全监督参考图像分割B、基于 Box 的实例分割C、带有噪声标签的学习四、提出的方法A、概述B、伪标签生成目标轮廓预测Proposal 选…...

Linux进程和任务管理和分析和排查系统故障
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...

【满分】【华为OD机试真题2023 JAVA】最多几个直角三角形
华为OD机试真题,2023年度机试题库全覆盖,刷题指南点这里 最多几个直角三角形 知识点递归深搜 时间限制:1s 空间限制:256MB 限定语言:不限 题目描述: 有N条线段,长度分别为a[1]-a[N]。现要求你计算这N条线段最多可以组合成几个直角三角形,每条线段只能使用一次,每个三…...
PyQt5可视化 7 饼图和柱状图实操案例 ②建表建项目改布局
目录 一、数据库建表 1 建表 2 插入数据 3 查看表数据 二、建立项目 1 新建项目 2 appMain.py 3 myMainWindow.py 4 myChartView.py 2.4.1 提升的后果 2.4.2 QmyChartView类说明 2.4.3 添加代码 三、修改myMainWindow.py程序,添加功能 1 打开数据库 …...
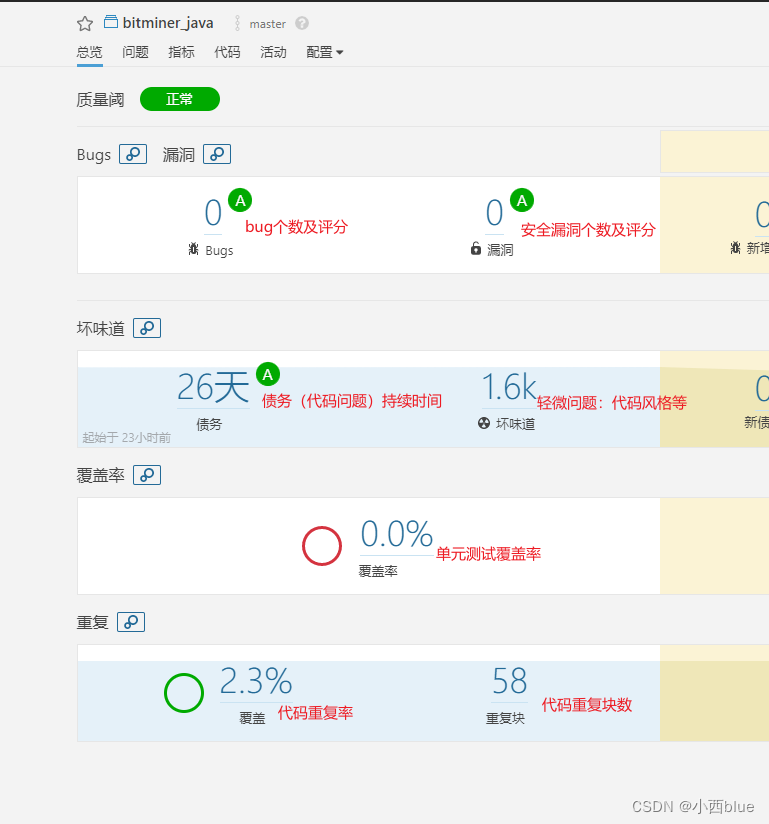
sonarqube指标详解
最近公司引入了sonar,作为代码质量检测工具,以期提高研发同学的代码质量,但是结果出来后,有些同学不清楚相应的指标内容,不知道应该重点关注哪些指标,于是查询了一下相关的资料,加以总结同时也分…...

耳机 喇叭接线分析
1 注意 1 首先必须接地 2 接某一个声道 2 分析 从三段式耳机结构可以得出: 模拟数据 必须的 结构 1 地 2 左or右信号 附加 我们要注意 耳机也是分左声道 右声道的 参考:耳机插头3.5与2.5三段与四段i版与n版等详解 在iPhone还没现在这么NB的时候&a…...

SpaceNet 建筑物检测
SpaceNet 建筑物检测 该存储库提供了一些 python 脚本和 jupyter 笔记本来训练和评估从SpaceNet卫星图像中提取建筑物的卷积神经网络。 用法...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
