牛客 NC129 阶乘末尾0的数量【简单 基础数学 Java/Go/PHP/C++】
题目

题目链接:
https://www.nowcoder.com/practice/aa03dff18376454c9d2e359163bf44b8
https://www.lintcode.com/problem/2
思路

Java代码
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** the number of 0* @param n long长整型 the number* @return long长整型*/public long thenumberof0 (long n) {//就是可以转换成求有多少个5,然后求每个5的倍数的数中有多少个5.最后将所有5的个数加一起long ans =0;while(n > 0){n =n/5;ans+=n;}return ans;}
}
Go代码
package main/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** the number of 0* @param n long长整型 the number* @return long长整型*/
func thenumberof0(n int64) int64 {//就是可以转换成求有多少个5,然后求每个5的倍数的数中有多少个5.最后将所有5的个数加一起var ans int64= 0for n > 0 {n = n / 5ans += n}return ans
}PHP代码
<?php/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** the number of 0* @param n long长整型 the number* @return long长整型*/
function thenumberof0( $n )
{//就是可以转换成求有多少个5,然后求每个5的倍数的数中有多少个5.最后将所有5的个数加一起$ans =0;while($n >0){$n = intval($n/5);$ans+=$n;}return $ans;
}
C++代码
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** the number of 0* @param n long长整型 the number* @return long长整型*/long long thenumberof0(long long n) {//就是可以转换成求有多少个5,然后求每个5的倍数的数中有多少个5.最后将所有5的个数加一起long ans =0;while(n >0){n=n/5;ans+=n;}return ans;}
};
相关文章:

牛客 NC129 阶乘末尾0的数量【简单 基础数学 Java/Go/PHP/C++】
题目 题目链接: https://www.nowcoder.com/practice/aa03dff18376454c9d2e359163bf44b8 https://www.lintcode.com/problem/2 思路 Java代码 import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改ÿ…...

【Spring Boot】异常处理
异常处理 1.认识异常处理1.1 异常处理的必要性1.2 异常的分类1.3 如何处理异常1.3.1 捕获异常1.3.2 抛出异常1.3.4 自定义异常 1.4 Spring Boot 默认的异常处理 2.使用控制器通知3.自定义错误处理控制器3.1 自定义一个错误的处理控制器3.2 自定义业务异常类3.2.1 自定义异常类3…...

Laravel学习-自定义辅助函数
因为laravel框架的辅助函数helpers不会进入版本库,被版本库忽略的,只有自己创建一个helpers辅助函数。 可以在任意文件下创建helpers.php文件,建议在app目录下, 然后在composer.json文件中,autoload 中间,…...

LLVM Cpu0 新后端6
想好好熟悉一下llvm开发一个新后端都要干什么,于是参考了老师的系列文章: LLVM 后端实践笔记 代码在这里(还没来得及准备,先用网盘暂存一下): 链接: https://pan.baidu.com/s/1yLAtXs9XwtyEzYSlDCSlqw?…...
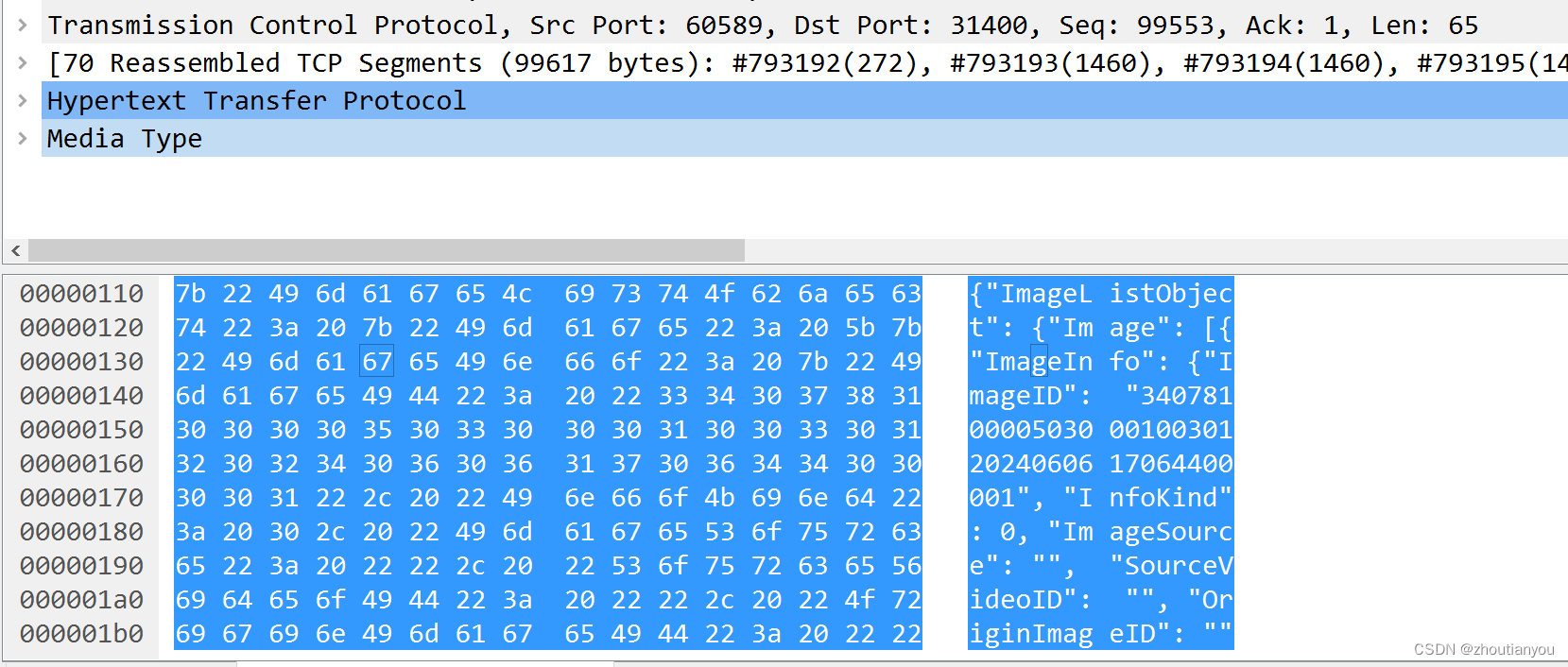
GAT1399协议分析(9)--图像上传
一、官方定义 二、wirechark实例 有前面查询的基础,这个接口相对简单很多。 请求: 文本化: POST /VIID/Images HTTP/1.1 Host: 10.0.201.56:31400 User-Agent: python-requests/2.32.3 Accept-Encoding: gzip, deflate Accept: */* Connection: keep-alive content-type:…...

Spring ApplicationContext的getBean方法
Spring ApplicationContext的getBean方法 在Spring框架的ApplicationContext中,getBean(Class<T> requiredType)方法可以接受一个类类型参数,这个参数可以是接口类也可以是实现类。 使用接口类: 如果requiredType是一个接口,…...
—— 自动摘要)
自然语言处理(NLP)—— 自动摘要
自动摘要是一种将长文本信息浓缩为短文本的技术,旨在保留原文的主要信息和意义。 1 自动摘要的第一种方法 它的第一种方法是基于理解的,受认知科学和人工智能的启发。 在这个方法中,我们首先建立文本的语义表示,这可以理解为文本…...

Spring RestClient报错:400 Bad Request : [no body]
我项目采用微服务架构,所以各服务之间通过Spring RestClient远程调用,本来一直工作得好好的,昨天突然发现远程调用一直报错,错误详情如下: org.springframework.web.client.HttpClientErrorException$BadRequest: 400…...
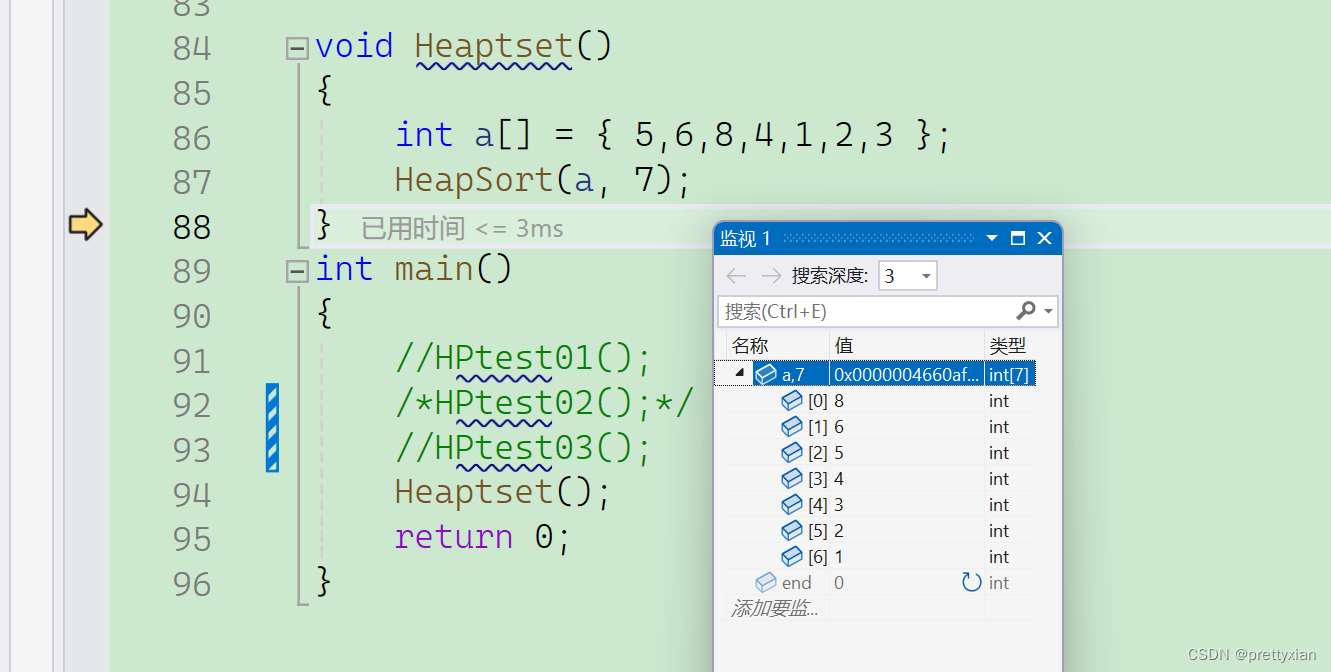
【数据结构】 -- 堆 (堆排序)(TOP-K问题)
引入 要学习堆,首先要先简单的了解一下二叉树,二叉树是一种常见的树形数据结构,每个节点最多有两个子节点,通常称为左子节点和右子节点。它具有以下特点: 根节点(Root):树的顶部节…...

C#面:XML与 HTML 的主要区别是什么
C# XML与HTML有以下几个主要区别: 用途不同:XML(eXtensible Markup Language)是一种用于存储和传输数据的标记语言,它的主要目的是描述数据的结构和内容。HTML(HyperText Markup Language)是一…...

java并发-如何保证线程按照顺序执行?
【readme】 使用只有单个线程的线程池(最简单)Thread.join() 可重入锁 ReentrantLock Condition 条件变量(多个) ; 原理如下: 任务1执行前在锁1上阻塞;执行完成后在锁2上唤醒;任务…...

PyCharm中 Fitten Code插件的使用说明一
一. 简介 Fitten Code插件是是一款由非十大模型驱动的 AI 编程助手,它可以自动生成代码,提升开发效率,帮您调试 Bug,节省您的时间,另外还可以对话聊天,解决您编程碰到的问题。 前一篇文章学习了 PyCharm…...
Polar Web【简单】PHP反序列化初试
Polar Web【简单】PHP反序列化初试 Contents Polar Web【简单】PHP反序列化初试思路EXP手动脚本PythonGo 运行&总结 思路 启动环境,显示下图中的PHP代码,于是展开分析: 首先发现Easy类中有魔术函数 __wakeup() ,实现的是对成员…...
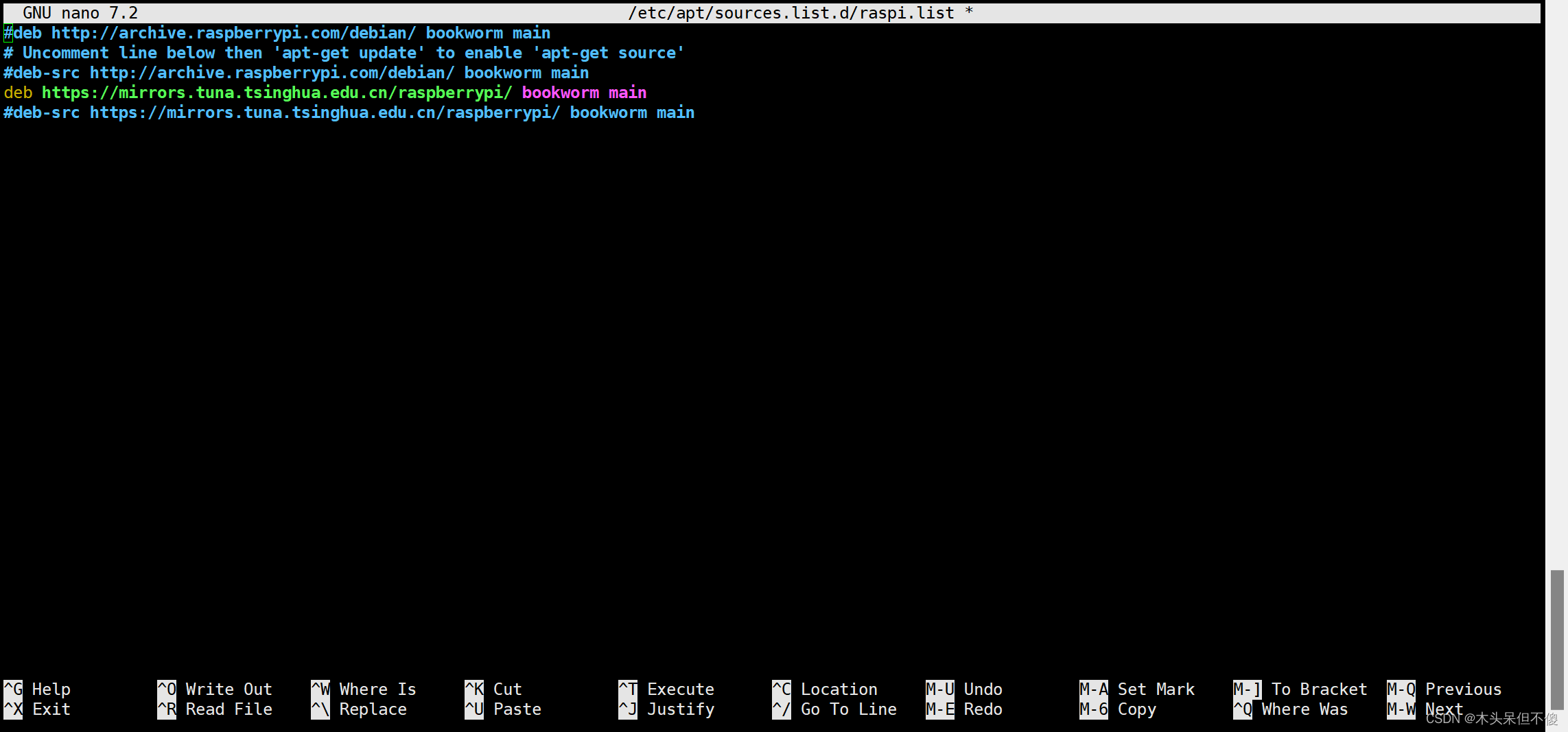
树莓派4B 零起点(二) 树莓派 更换软件源和软件仓库
目录 一、准备工作,查看自己的树莓派版本 二、安装HTTPS支持 三、更换为清华源 1、更换Debian软件源 2,更换Raspberrypi软件仓库 四、进行软件更新 接前章,我们的树莓派已经启动起来了,接下来要干的事那就是更换软件源和软件…...
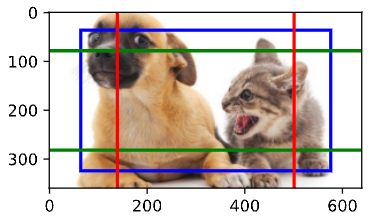
Pytorch 实现目标检测二(Pytorch 24)
一 实例操作目标检测 下面通过一个具体的例子来说明锚框标签。我们已经为加载图像中的狗和猫定义了真实边界框,其中第一个 元素是类别(0代表狗,1代表猫),其余四个元素是左上角和右下角的(x, y)轴坐标(范围…...
进行高效列表操作)
如何使用Python中的列表解析(list comprehension)进行高效列表操作
Python中的列表解析(list comprehension)是一种创建列表的简洁方法,它可以在单行代码中执行复杂的循环和条件逻辑。列表解析提供了一种快速且易于阅读的方式来生成新的列表。 以下是一些使用列表解析进行高效列表操作的示例: 1.…...

java使用websocket遇到的问题
java使用websocket的bug 1 websocket连接正常但是收不到服务端发出的消息java的websocket并发的时候导致连接断开(看着连接是正常的,但是实际上已经断开) 1 websocket连接正常但是收不到服务端发出的消息 java的websocket并发的时候导致连接断…...

[Cloud Networking] Layer 2
文章目录 1. 什么是Mac Address?2. 如何查找MAC地址?3. 二层数据交换4. [Layer 2 Protocol](https://blog.csdn.net/settingsun1225/article/details/139552315) 1. 什么是Mac Address? MAC 地址是计算机的唯一48位硬件编码,嵌入到网卡中。 MAC地址也…...
)
[240609] qwen2 发布,在 Ollama 已可用 | 采用语言模型构建通用 AGI(2020年8月)
目录 qwen2 发布,在 Ollama 已可用Qwen2 模型概览 (基于 Ollama 网站信息)一、模型介绍二、模型参数三、支持语言 (除英语和中文外)四、模型性能五、许可证六、数据支撑: 采用语言模型构建通用 AGI qwen2 发布,在 Ollama 已可用 Qwen2 模型概览 (基于 O…...
)
赶紧收藏!2024 年最常见 20道分布式、微服务面试题(五)
上一篇地址:赶紧收藏!2024 年最常见 20道分布式、微服务面试题(四)-CSDN博客 九、在分布式系统中,如何保证数据一致性? 在分布式系统中保证数据一致性是一个复杂的问题,因为分布式系统由多个独…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
