算法家族之一——二分法
目录
- 算法
- 算法的打印效果
- 如果算法里的整型“i”为1
- 如果算法里的整型“i”为11
- 算法的流程图
- 算法的实际应用
- 总结
大家好,我叫 这是我58,现在,请看下面的算法。
算法
#define _CRT_SECURE_NO_WARNINGS 1//<--预处理指令
#include <stdio.h><--也是预处理指令
int main() {int arr[10] = { 1,2,3,4,5,6,7,8,9,10 };//<--在哪里查int i = 1;//<--需要查的数int right = sizeof arr / sizeof arr[0]-1;int left = 0;int mid = 0;while (left <= right) {mid = (left + right) / 2;if (arr[mid] < i) { left = ++mid; }else if (arr[mid] > i) { right = --mid; }else {printf("i(%d)在arr数组里的第%d个位置",i,mid);break;}if (left > right) { printf("在arr数组里,没有“i”这个数字"); }}return 0;
}
相信大家都对这个算法不陌生吧,没错!这个算法就是我们的二分法!那么,有的人可能就不相信这个算法能正确地运行起来了,现在,如果你是这些人中的其中一个的话,就先看一下下面的内容再说吧。而且,还有这个算法的流程图呢!
算法的打印效果
如果算法里的整型“i”为1
i(1)在arr数组里的第0个位置
如果算法里的整型“i”为11
在arr数组里,没有“i”这个数字
算法的流程图
算法的实际应用
在刚才看完上面的内容后,你可能觉得这个算法只要没记牢就不知道怎么写了,但是,刚开始的确是这样的,可是在后来,你只要年复一年,日复一日地写这个算法,等到后来啊,就基本能够在没有看这个算法的时候写出这个算法了,并且,在能够在没有看这个算法的时候写出这个算法的时候,你就可以更方便地做下面的三件小事了。
- 用来求方程的近似值,就比如在公式“ f ( x ) = l n ( x ) + 2 x − 6 f(x)=ln(x)+2x-6 f(x)=ln(x)+2x−6”中,只用了4次二分法就精确到了0.1。12
- 用来更快速地修好电路、水管、气管(只要用几次二分法,就能精准地查找并修好电路、水管或者气管的故障了)。2
- 用来更快地找出次品,就比如在12个从外表上来看几乎一模一样的球中,有一个次品球,这个次品球比其他球略轻,而只要用几次二分法,就可以较快地用天平找出那个次品球。32
总结
在看完这篇博客之后,我想你应该爱上了算法家族之一——二分法了吧。那么,如果你喜欢上了算法家族之一——二分法的话,可以评论或者投票来互动一下我哦。
选自搜狗问问中的名叫“用二分法求函数f(x)=lnx+2x-6在区间(2,3)零点近似值,至少经过( )次二分后精确度达到0.1.A.2”的问题 ↩︎
 ↩︎ ↩︎ ↩︎
↩︎ ↩︎ ↩︎选自百度文库中的其中一篇“二分法在生活中的应用.” ↩︎
相关文章:

算法家族之一——二分法
目录 算法算法的打印效果如果算法里的整型“i”为1如果算法里的整型“i”为11 算法的流程图算法的实际应用总结 大家好,我叫 这是我58,现在,请看下面的算法。 算法 #define _CRT_SECURE_NO_WARNINGS 1//<--预处理指令 #include <stdi…...
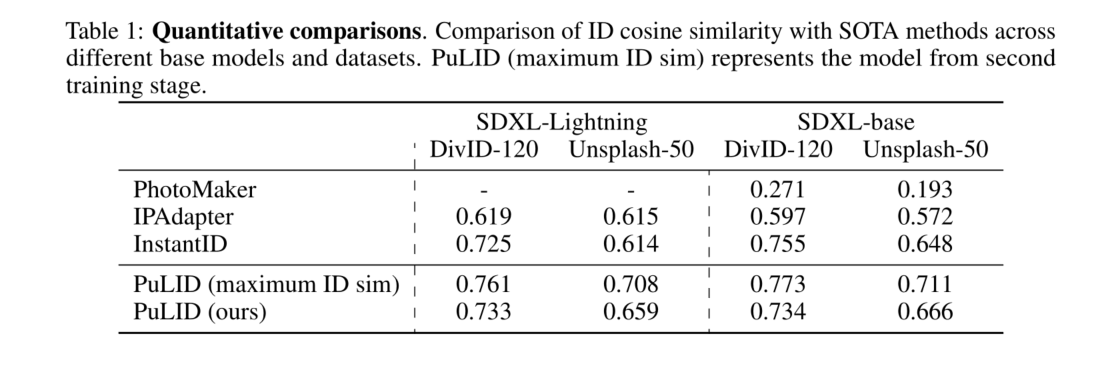
【深度学习】PuLID: Pure and Lightning ID Customization via Contrastive Alignment
论文:https://arxiv.org/abs/2404.16022 代码:https://github.com/ToTheBeginning/PuLID 文章目录 AbstractIntroductionRelated WorkMethods Abstract 我们提出了一种新颖的、无需调整的文本生成图像ID定制方法——Pure and Lightning ID customizatio…...

Elastic 8.14:用于简化分析的 Elasticsearch 查询语言 (ES|QL) 正式发布
作者:来自 Elastic Brian Bergholm 今天,我们很高兴地宣布 Elastic 8.14 正式发布。 什么是新的? 8.14 版本最重要的标题是 ES|QL 的正式发布(GA),它是从头开始设计和专门构建的,可大大简化数据调查。在新的查询引擎的…...

C语言指针与数组的区别
在C语言中,指针和数组虽然在很多情况下可以互换使用,但它们在概念上和行为上存在一些区别。下面详细解释这些区别: ### 数组 1. **固定大小**:数组在声明时必须指定大小,这个大小在编译时确定,之后不能改…...

springboot3一些听课笔记
文章目录 一、错误处理机制1.1 默认1.2 自定义 二、嵌入式容器 一、错误处理机制 1.1 默认 错误处理的自动配置都在ErrorMvcAutoConfiguration中,两大核心机制: ● 1. SpringBoot 会自适应处理错误,响应页面或JSON数据 ● 2. SpringMVC的错…...

【小沐学Python】Python实现Web服务器(CentOS下打包Flask)
文章目录 1、简介2、下载Python3、编译Python4、安装PyInstaller5、打包PyInstaller6、相关问题6.1 ImportError: urllib3 v2 only supports OpenSSL 1.1.1, currently the ssl module is compiled with OpenSSL 1.0.2k-fips 26 Jan 2017. See: https://github.com/urllib3/url…...

Cesium开发环境搭建(一)
1.下载安装Node.js 进入官网地址下载安装包 Node.js — Download Node.js https://cdn.npmmirror.com/binaries/node/ 选择对应你系统的Node.js版本,这里我选择的是Windows系统、64位 安装完成后,WINR,输入node --version,显示…...
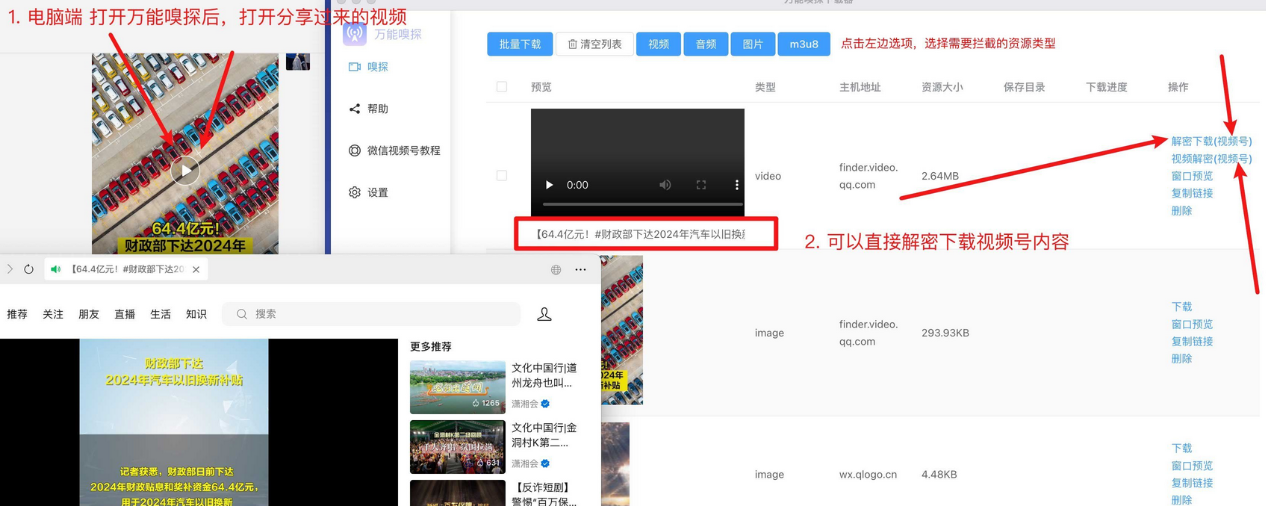
视频、图片、音频资源抓取(支持视频号),免安装,可批量,双端可用!
今天分享一款比较好用资源嗅探软件,这个嗅探工具可以下载视频号,界面干净,可以内容预览和批量下载,看到这里你是不是想用它爬很多不得了的东西。这款软件无需安装,打开即用。同时他支持windows系统和Mac系统,是一款不可…...
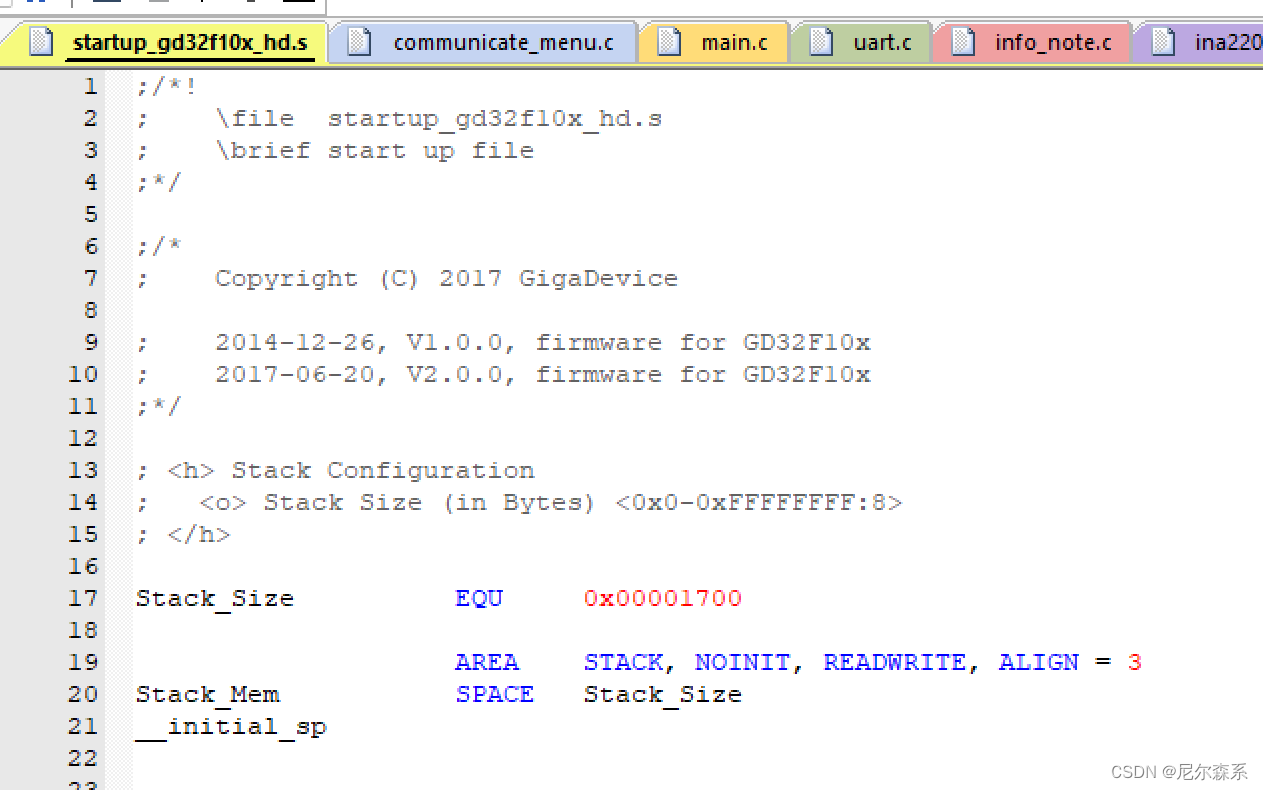
FreeRTOS实时系统 在任务中增加数组等相关操作 导致单片机起不来或者挂掉
在调试串口任务中增加如下代码,发现可以用keil进行仿真,但是烧录程序后,调试串口没有打印,状态灯也不闪烁,单片机完全起不来 博主就纳了闷了,究竟是什么原因,这段代码可是公司永流传的老代码了&…...

CentOS 7基础操作08_Linux查找目录和文件
1、which命令——查找用户所执行的命令文件存放的目录 which命令用于查找Linux命令程序并显示所在的具体位置.其搜索范围主要由用户的环境变量PATH决定(可以执行言echo sPATH”命令查看),这个范围也是Linux操作系统在执行命令或程序时的默认搜索路径。 which命令使用要查找的命…...

CI/CD实战面试宝典:从构建到高可用性的全面解析
实战部署与配置 请描述你设计和实现的一个CI/CD pipeline的完整流程,包括构建、测试、部署各个阶段。 我设计的CI/CD pipeline通常包括以下几个阶段: 代码提交:开发人员将代码提交到Git仓库,触发CI/CD流程。代码检查࿱…...
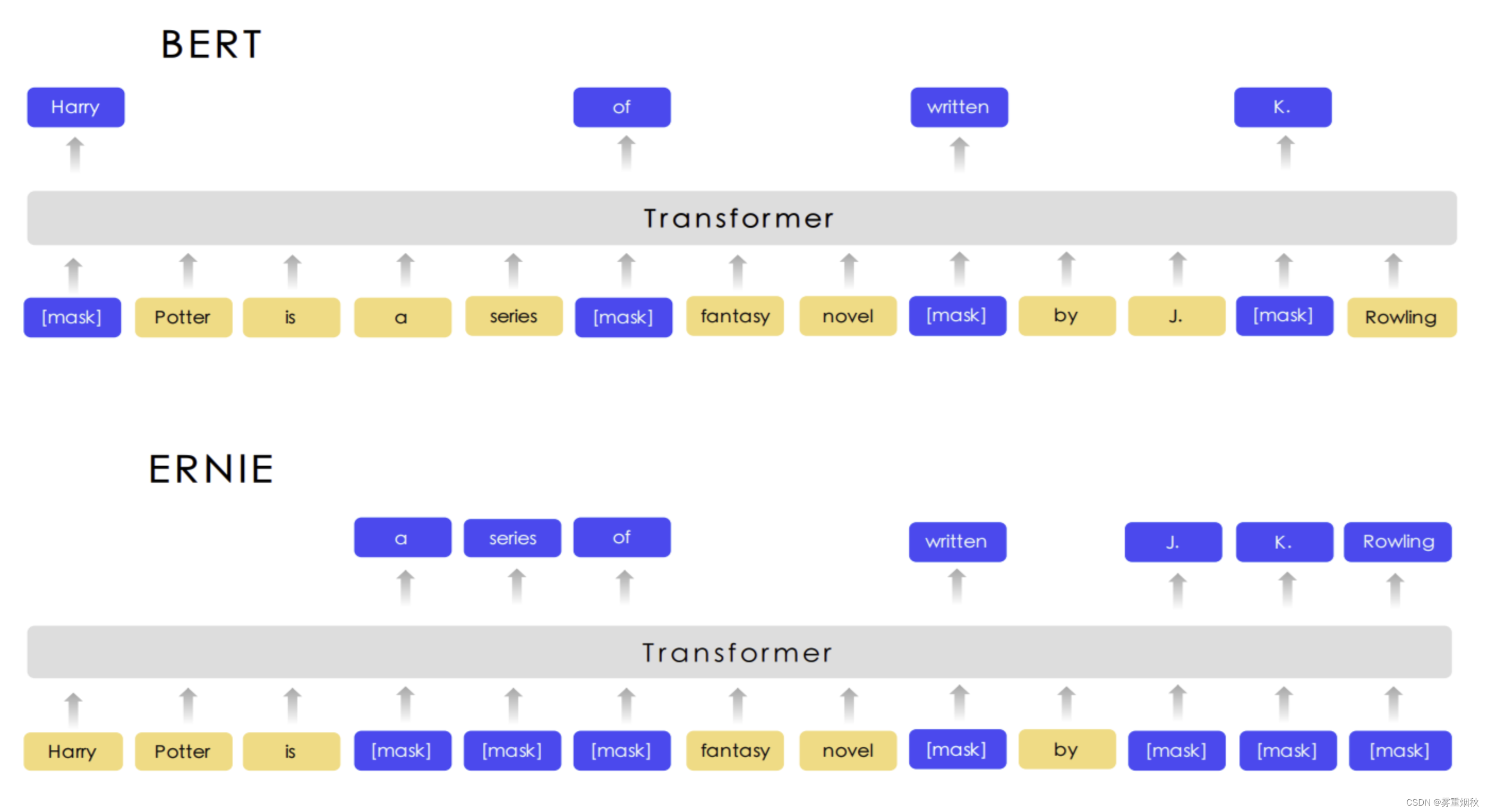
NLP实战入门——文本分类任务(TextRNN,TextCNN,TextRNN_Att,TextRCNN,FastText,DPCNN,BERT,ERNIE)
本文参考自https://github.com/649453932/Chinese-Text-Classification-Pytorch?tabreadme-ov-file,https://github.com/leerumor/nlp_tutorial?tabreadme-ov-file,https://zhuanlan.zhihu.com/p/73176084,是为了进行NLP的一些典型模型的总…...
MySQL: 表的增删改查(基础)
文章目录 1. 注释2. 新增(Create)3. 查询(Retrieve)3.1 全列查询3.2 指定列查询3.3 查询字段为表达式3.4 别名3.5 去重: distinct3.6 排序: order by3.7条件查询3.8 分页查询 4. 修改 (update)5. 删除(delete)6. 内容重点总结 1. 注释 注释:在SQL中可以使用“–空格…...
WDF驱动开发-PNP和电源管理(三)
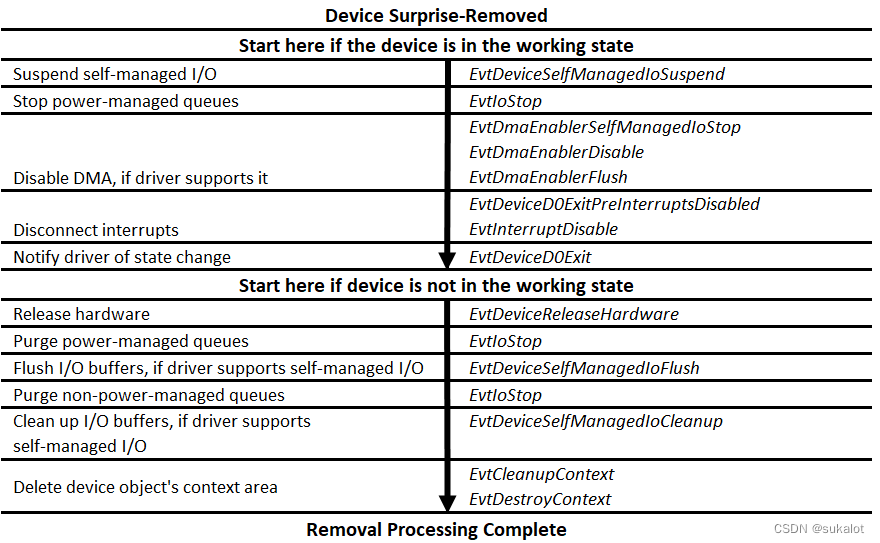
对于PNP设备来说,理解它们的启动和删除顺序,以及意外移除顺序非常重要,在早期,经常有拔插U盘导致windows重启的例子,这就是意外移除带来的问题。 功能或Filter驱动程序的启动顺序 下图显示了框架调用 WDF (KMDF 和 U…...

Redis集群和高可用性:保障Redis服务的稳定性
I. 引言 A. 对Redis的简单介绍和其在现代Web应用中的角色 Redis(REmote DIctionary Server)是一个开源的、基于内存的键值数据库,它支持多种数据结构,如字符串、哈希、列表、集合、有序集合等。由于Redis的高性能和丰富的数据类型,使其在现代Web应用中广泛使用。例如,它…...
C# WPF入门学习主线篇(二十一)—— 静态资源和动态资源
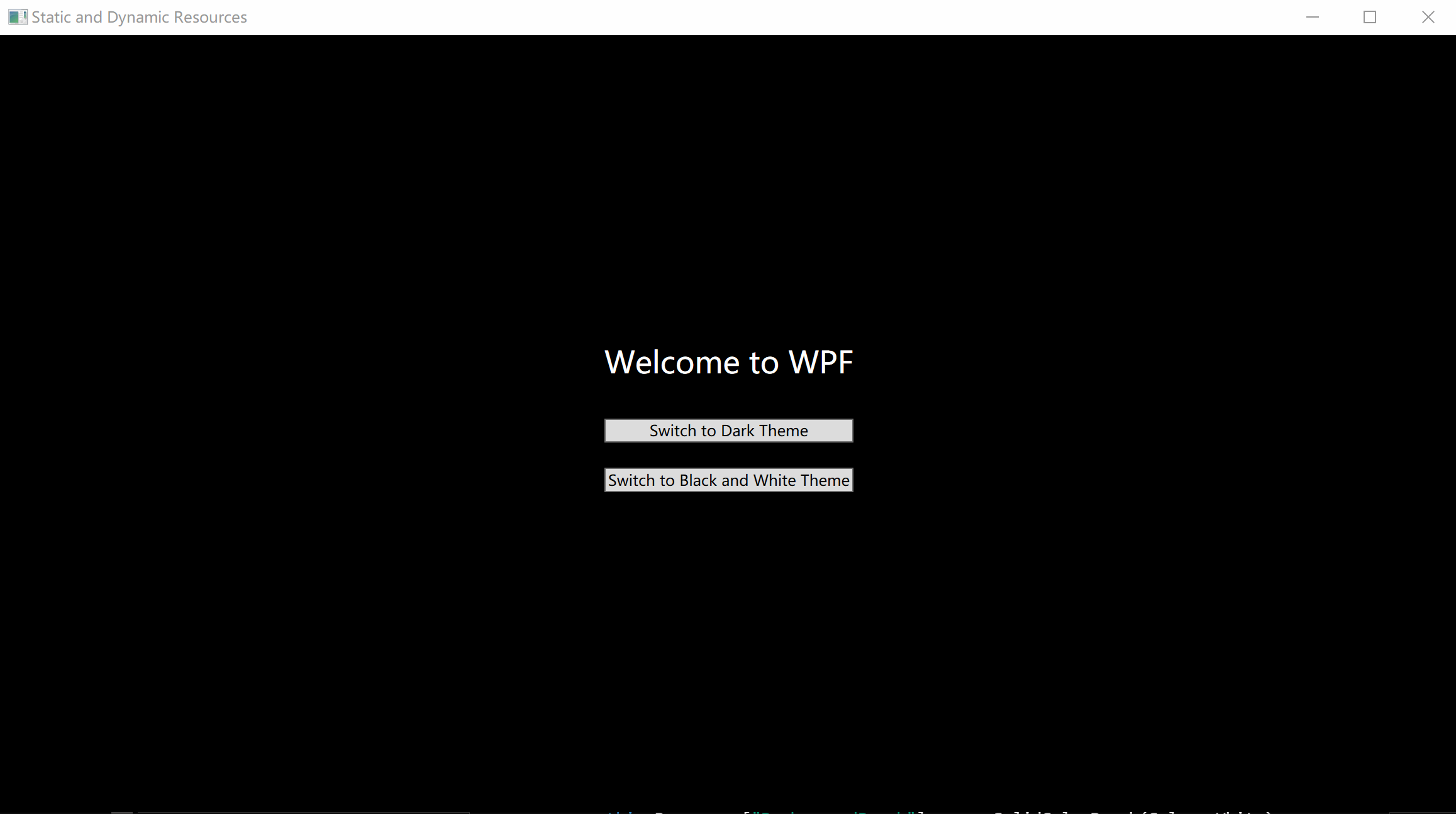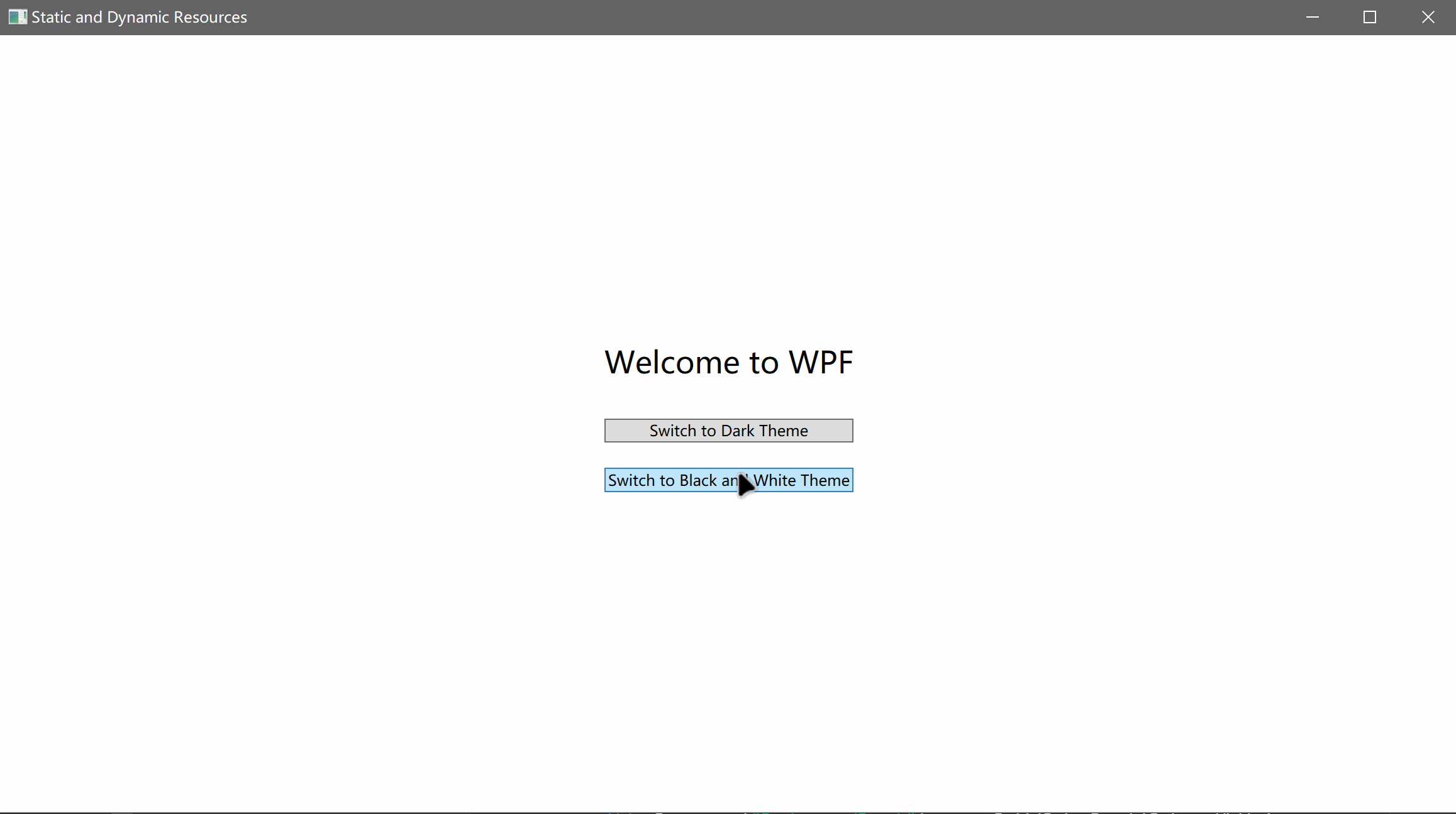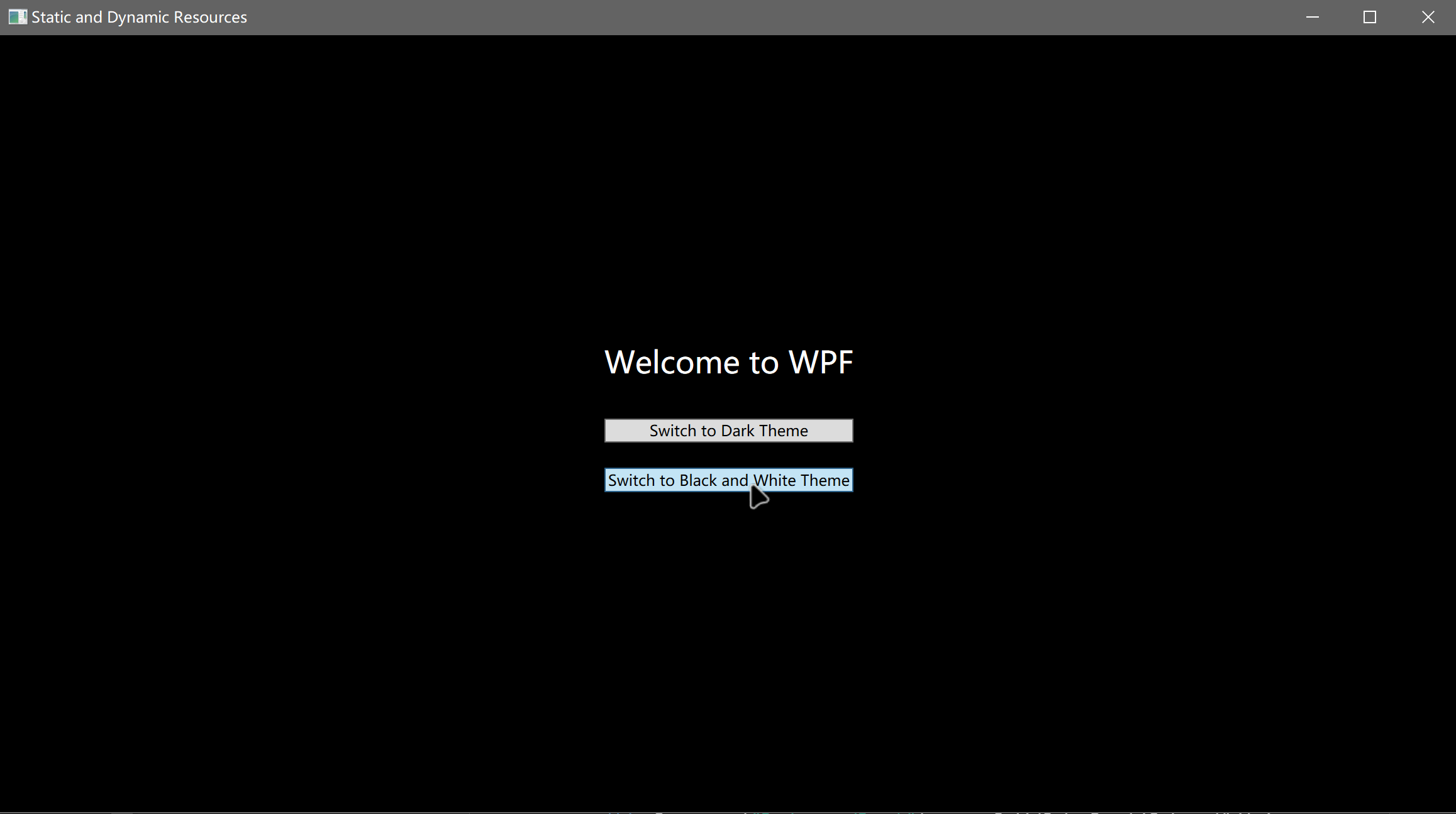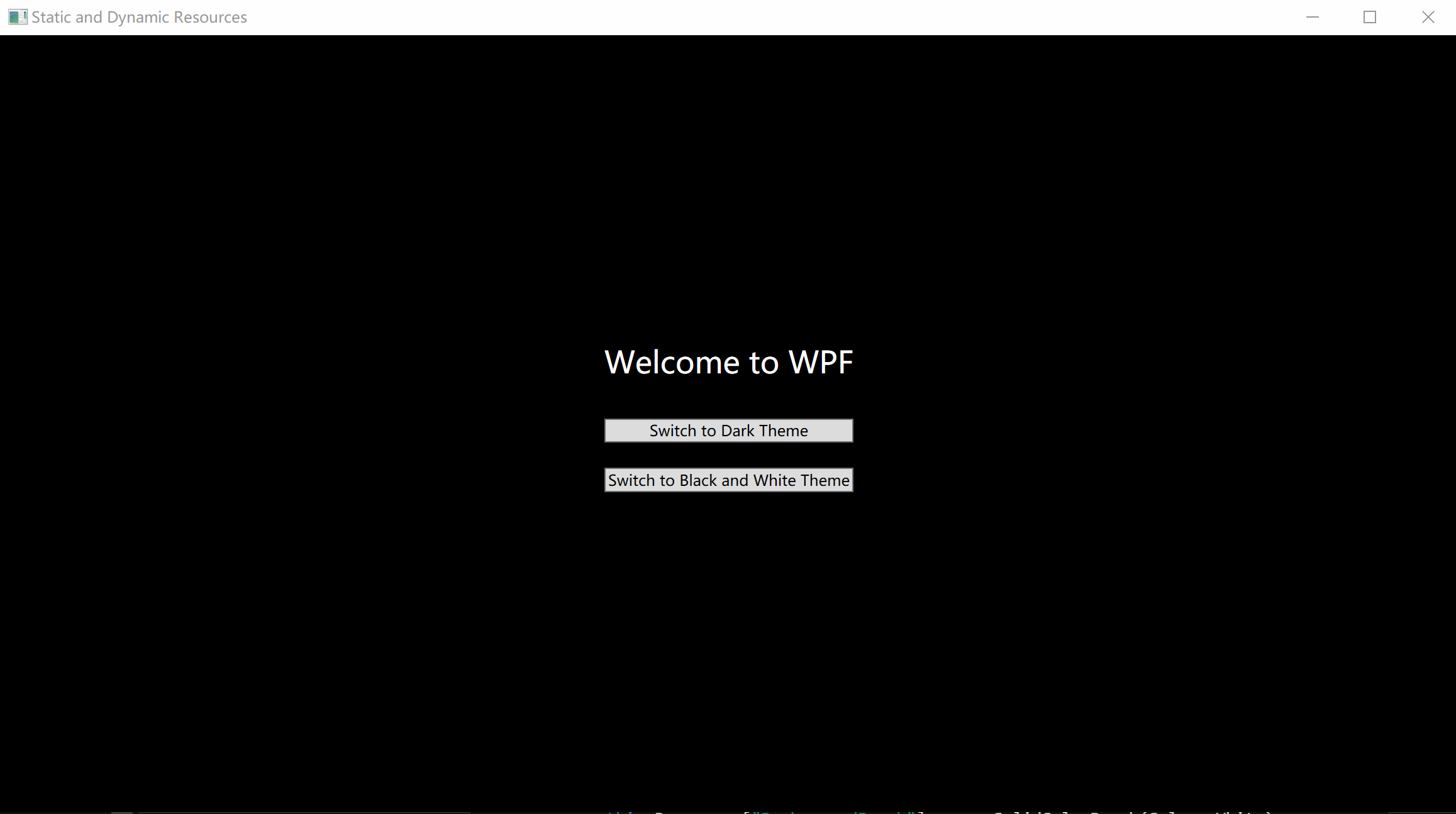
C# WPF入门学习主线篇(二十一)—— 静态资源和动态资源 欢迎来到C# WPF入门学习系列的第二十一篇。在上一章中,我们介绍了WPF中的资源和样式。本篇文章将深入探讨静态资源(StaticResource)和动态资源(Dynam…...
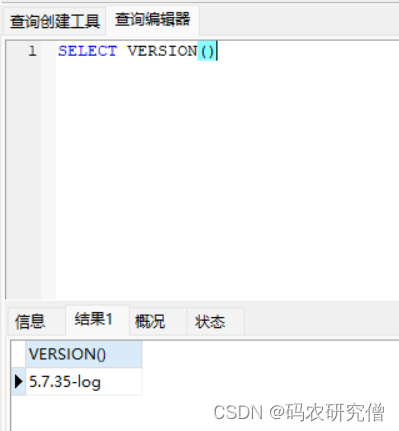
出现 Navicat 和 Cmd 下SQL 版本 | 查询不一致的解决方法
目录 1. 问题所示1.1 查询表格不一致1.2 版本不一致2. 原理分析3. 解决方法1. 问题所示 命令行和数据库使用工具出现不一致的情况,分别有如下情况 1.1 查询表格不一致 使用工具查询当地表格: 使用命令行查询当地表格: 1.2 版本不一致 在cmd命令下mysql --version 查询…...
31、matlab卷积运算:卷积运算、二维卷积、N维卷积
1、conv 卷积和多项式乘法 语法 语法1:w conv(u,v) 返回向量 u 和 v 的卷积。 语法2:w conv(u,v,shape) 返回如 shape 指定的卷积的分段。 参数 u,v — 输入向量 shape — 卷积的分段 full (默认) | same | valid full:全卷积 ‘same…...

C++青少年简明教程:文件
C青少年简明教程:文件 文件是指存储在计算机文件系统中的数据集合。文件可以包含各种类型的信息,例如文本、图像、音频视频等。在 C中,文件是一种数据流,可以用于读取或写入数据。C提供了一系列的文件操作函数,用于实现…...
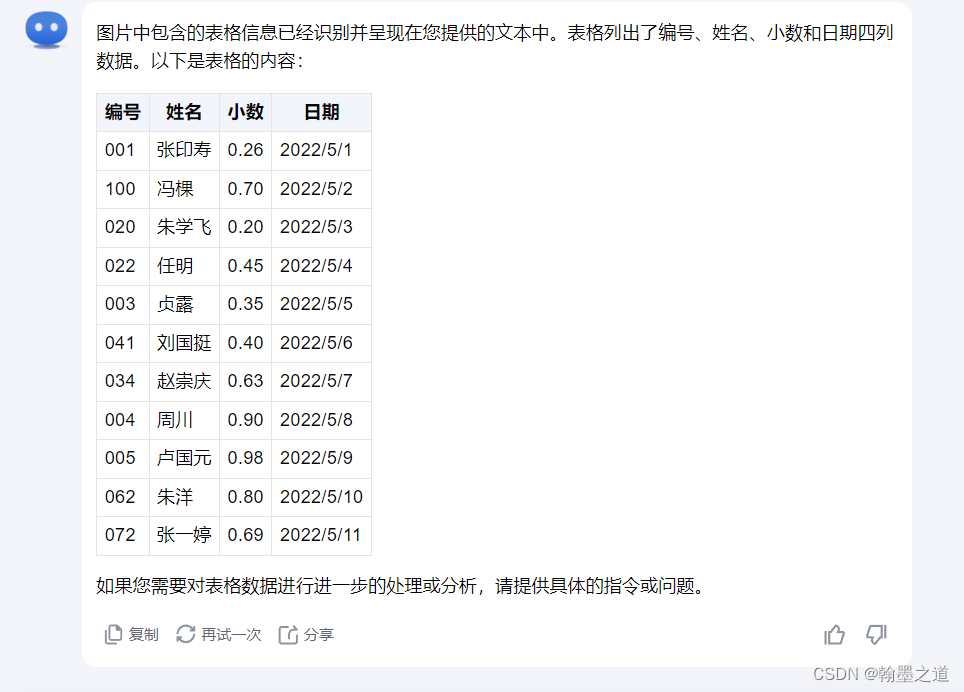
Kimichat使用案例010:快速识别出图片中的表格保存到Excel
文章目录 一、介绍二、图片信息三、输入内容四、输出内容五、markdown提示词六、markdown输出一、介绍 如果有一张图片格式的表格,想要快速复制到Excel表格中,那么一般要借助于OCR工具。之前试过不少在线OCR工具,识别效果差强人意。其实,kimichat就可以非常好的完成这个任务…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
