Leetcode.866 回文质数
题目链接
Leetcode.866 回文质数
rating : 1938
题目描述
给你一个整数 n n n ,返回大于或等于 n n n 的最小 回文质数。
一个整数如果恰好有两个除数: 1 1 1 和它本身,那么它是 质数 。注意, 1 1 1 不是质数。
- 例如, 2 、 3 、 5 、 7 、 11 2、3、5、7、11 2、3、5、7、11 和 13 13 13 都是质数。
一个整数如果从左向右读和从右向左读是相同的,那么它是 回文数 。
- 例如, 101 101 101 和 12321 12321 12321 都是回文数。
测试用例保证答案总是存在,并且在 [ 2 , 2 × 1 0 8 ] [2, 2 \times 10^8] [2,2×108] 范围内。
示例1:
输入:n = 6
输出:7
示例2:
输入:n = 8
输出:11
示例3:
输入:n = 13
输出:101
提示:
- 1 ≤ n ≤ 1 0 8 1 \leq n \leq 10^8 1≤n≤108
解法:数学 + 判断质数
对于 回文数 ,我们可以得出这么一个结论:任何一个大于 11 11 11 的偶数长度的回文数,一定是 11 11 11 的倍数。
证明如下:
- 1 0 0 = 1 m o d 11 = 1 10 ^ 0 = 1 \ mod \ 11 = 1 100=1 mod 11=1
- 1 0 1 = 10 m o d 11 = 10 10 ^ 1 = 10 \ mod \ 11 = 10 101=10 mod 11=10
- 1 0 2 = 100 m o d 11 = 1 10 ^ 2 = 100 \ mod \ 11 = 1 102=100 mod 11=1
- 1 0 3 = 1000 m o d 11 = 10 10 ^ 3 = 1000 \ mod \ 11 = 10 103=1000 mod 11=10
- 1 0 4 = 10000 m o d 11 = 1 10 ^ 4 = 10000 \ mod \ 11 = 1 104=10000 mod 11=1
- …
根据数学归纳法,我们可以得出这样的结论:
- n n n 为偶数,那么 1 0 n m o d 11 = 1 10 ^ n \ mod \ 11 = 1 10n mod 11=1
- n n n 为奇数,那么 1 0 n m o d 11 = 10 10 ^ n \ mod \ 11 = 10 10n mod 11=10
假设回文数 P P P 一共有 2 n 2n 2n 位,从高到低分别为 a 1 a 2 a 3 a 4 . . . a n a n a n − 1 . . . a 2 a 1 a_1a_2a_3a_4...a_na_na_{n-1}...a_2a_1 a1a2a3a4...ananan−1...a2a1。
将其转换为十进制的形式如下:
P = a 1 × 1 0 2 n − 1 + a 2 × 1 0 2 n − 2 + . . . + a n × 1 0 n + a n × 1 0 n − 1 + . . . + a 2 × 10 + a 1 P = a_1\times10^{2n-1}+a_2\times10^{2n-2}+...+a_n\times10^n+a_n\times10^{n-1}+...+a_2\times10+a_1 P=a1×102n−1+a2×102n−2+...+an×10n+an×10n−1+...+a2×10+a1
如果对回文数 P P P 模 11 11 11,我们可以得到如下的结果:
P = a 1 × 10 + a 2 × 1 + a 3 × 10 + . . . a n × 10 + a n × 1 + . . . + a 2 × 10 + a 1 P = a_1 \times 10 + a_2\times1+a_3\times10+...a_n\times10+a_n\times1+...+a_2\times10+a1 P=a1×10+a2×1+a3×10+...an×10+an×1+...+a2×10+a1
将其整理一下得到如下结果:
P = a 1 × 11 + a 2 × 11 + a 3 × 11 + . . . + a n × 11 P = a_1 \times 11 + a_2\times11+a_3\times11+...+a_n\times11 P=a1×11+a2×11+a3×11+...+an×11
可以发现在对 P P P 模 11 11 11 的基础之上,剩下的余数依旧是 11 11 11,说明 11 11 11 可以整除 P P P,也就是 P P P 是 11 11 11 的倍数。
根据以上的证明,我们可以得出结论:
- 如果 n ≤ 11 n \leq 11 n≤11,那么只需要在 [ 2 , 11 ] [2, 11] [2,11] 中找到第一个大于等于 n n n 的质数返回即可。
- 如果 n > 11 n > 11 n>11,因为偶数长度的回文数全都不是质数,所以我们只需要判断奇数长度的回文数。由于是回文数,所以我们只需要获取前一半,后一半直接拼接上即可。所以只需要在 [ 10 , 19999 ] [10, 19999] [10,19999] 找到第一个大于等于 n n n 的回文质数 x x x 即可。
时间复杂度: O ( n 3 4 ) O(n^\frac{3}{4}) O(n43)
C++代码:
class Solution {
public:bool check(int x){if(x < 2) return false;for(int i = 2;i * i <= x;i++){if(x % i == 0) return false;}return true;}int primePalindrome(int k) {if(k <= 11){for(int i = 2;i <= 11;i++){if(i >= k && check(i)) return i;}}else{for(int i = 10;i <= 19999;i++){string s = to_string(i);int n = s.size();for(int i = n - 2;i >= 0;i--) s.push_back(s[i]);int x = stoi(s);if(x >= k && check(x)) return x;} }return -1;}
};
Python3代码:
def check(x: int) -> bool:if x < 2:return Falsei = 2while i * i <= x:if x % i == 0:return Falsei += 1return Trueclass Solution:def primePalindrome(self, k: int) -> int:if k <= 11:for i in range(2, 12):if i >= k and check(i):return ielse:for i in range(10, 20000):s = str(i)n = len(s)s = s + s[:n - 1][::-1]x = int(s)if x >= k and check(x):return xreturn -1
相关文章:

Leetcode.866 回文质数
题目链接 Leetcode.866 回文质数 rating : 1938 题目描述 给你一个整数 n n n ,返回大于或等于 n n n 的最小 回文质数。 一个整数如果恰好有两个除数: 1 1 1 和它本身,那么它是 质数 。注意, 1 1 1 不是质数。 例如…...
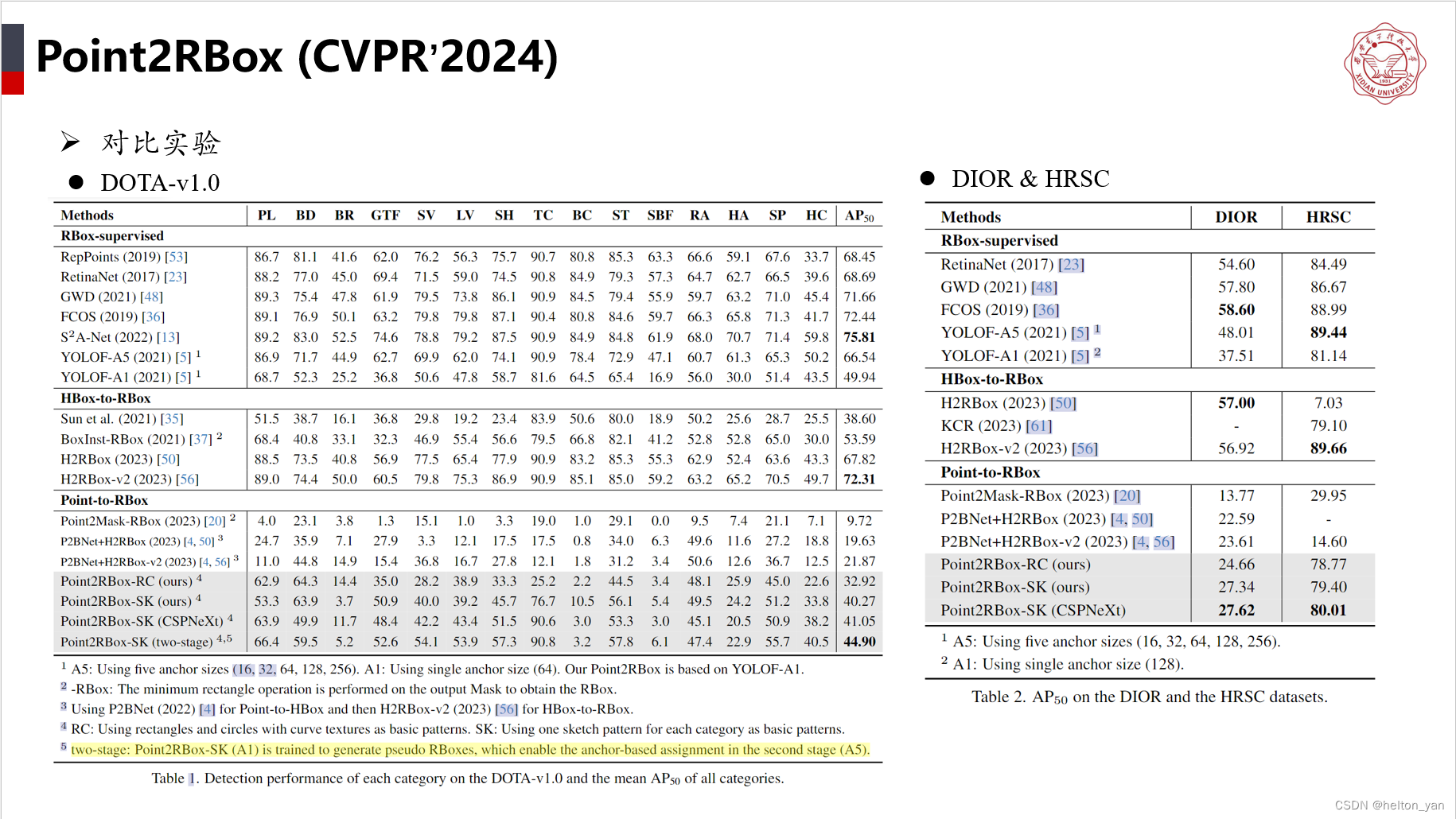
【论文阅读】Point2RBox (CVPR’2024)
paper:https://arxiv.org/abs/2311.14758 code:https://github.com/yuyi1005/point2rbox-mmrotate...

深度学习的点云分割
深度学习的点云分割 点云分割是计算机视觉中的一个重要任务,特别是在三维数据处理和分析中。点云数据是由大量三维点构成的集合,每个点包含空间坐标(x, y, z),有时还包含其他信息如颜色和法向量。点云分割的目标是将点…...

【知识点】c++模板特化
在 C 中,模板特化分为全特化(full specialization)和偏特化(partial specialization)。它们允许程序员为特定类型或类型模式提供不同的实现,以覆盖通用模板的默认行为。 模板全特化 模板全特化是指为某个…...

算法家族之一——二分法
目录 算法算法的打印效果如果算法里的整型“i”为1如果算法里的整型“i”为11 算法的流程图算法的实际应用总结 大家好,我叫 这是我58,现在,请看下面的算法。 算法 #define _CRT_SECURE_NO_WARNINGS 1//<--预处理指令 #include <stdi…...
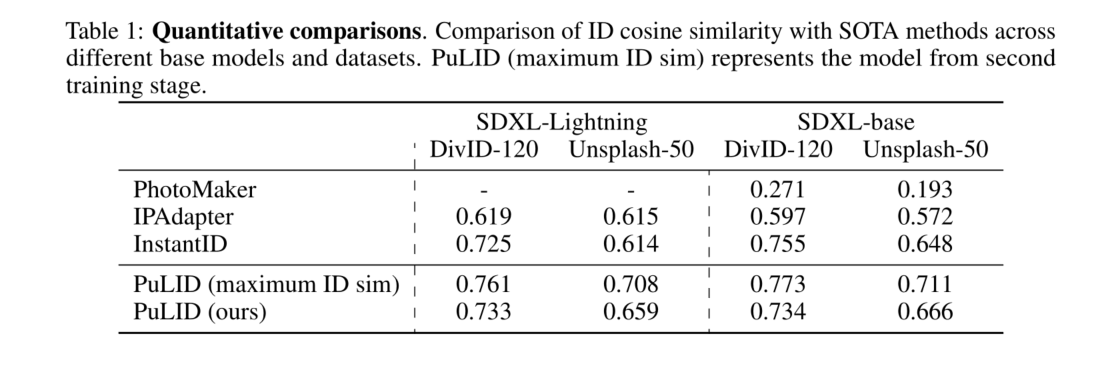
【深度学习】PuLID: Pure and Lightning ID Customization via Contrastive Alignment
论文:https://arxiv.org/abs/2404.16022 代码:https://github.com/ToTheBeginning/PuLID 文章目录 AbstractIntroductionRelated WorkMethods Abstract 我们提出了一种新颖的、无需调整的文本生成图像ID定制方法——Pure and Lightning ID customizatio…...

Elastic 8.14:用于简化分析的 Elasticsearch 查询语言 (ES|QL) 正式发布
作者:来自 Elastic Brian Bergholm 今天,我们很高兴地宣布 Elastic 8.14 正式发布。 什么是新的? 8.14 版本最重要的标题是 ES|QL 的正式发布(GA),它是从头开始设计和专门构建的,可大大简化数据调查。在新的查询引擎的…...

C语言指针与数组的区别
在C语言中,指针和数组虽然在很多情况下可以互换使用,但它们在概念上和行为上存在一些区别。下面详细解释这些区别: ### 数组 1. **固定大小**:数组在声明时必须指定大小,这个大小在编译时确定,之后不能改…...

springboot3一些听课笔记
文章目录 一、错误处理机制1.1 默认1.2 自定义 二、嵌入式容器 一、错误处理机制 1.1 默认 错误处理的自动配置都在ErrorMvcAutoConfiguration中,两大核心机制: ● 1. SpringBoot 会自适应处理错误,响应页面或JSON数据 ● 2. SpringMVC的错…...

【小沐学Python】Python实现Web服务器(CentOS下打包Flask)
文章目录 1、简介2、下载Python3、编译Python4、安装PyInstaller5、打包PyInstaller6、相关问题6.1 ImportError: urllib3 v2 only supports OpenSSL 1.1.1, currently the ssl module is compiled with OpenSSL 1.0.2k-fips 26 Jan 2017. See: https://github.com/urllib3/url…...

Cesium开发环境搭建(一)
1.下载安装Node.js 进入官网地址下载安装包 Node.js — Download Node.js https://cdn.npmmirror.com/binaries/node/ 选择对应你系统的Node.js版本,这里我选择的是Windows系统、64位 安装完成后,WINR,输入node --version,显示…...
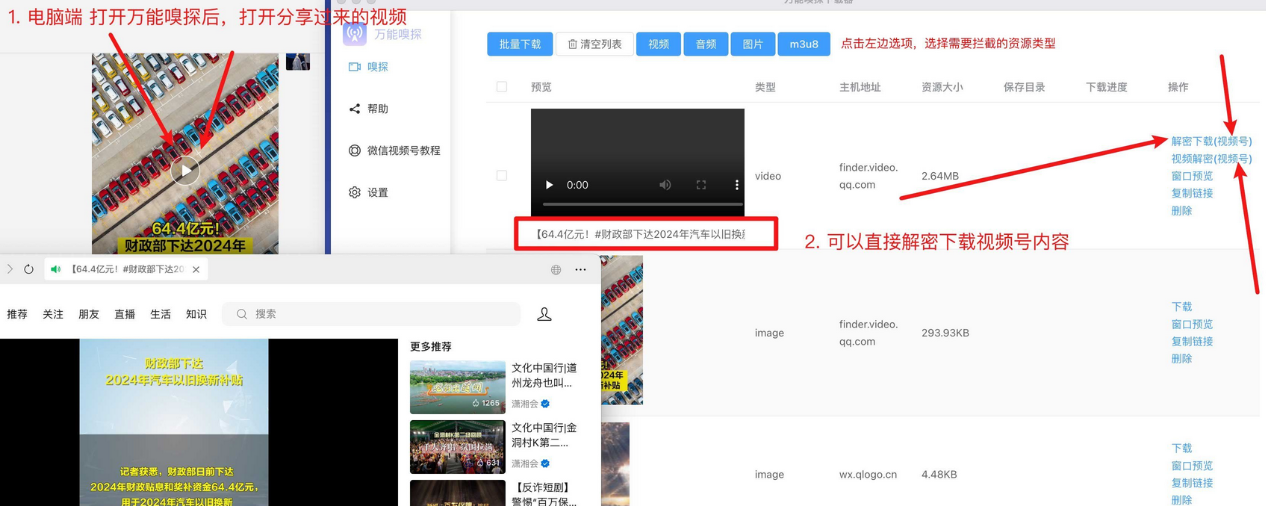
视频、图片、音频资源抓取(支持视频号),免安装,可批量,双端可用!
今天分享一款比较好用资源嗅探软件,这个嗅探工具可以下载视频号,界面干净,可以内容预览和批量下载,看到这里你是不是想用它爬很多不得了的东西。这款软件无需安装,打开即用。同时他支持windows系统和Mac系统,是一款不可…...
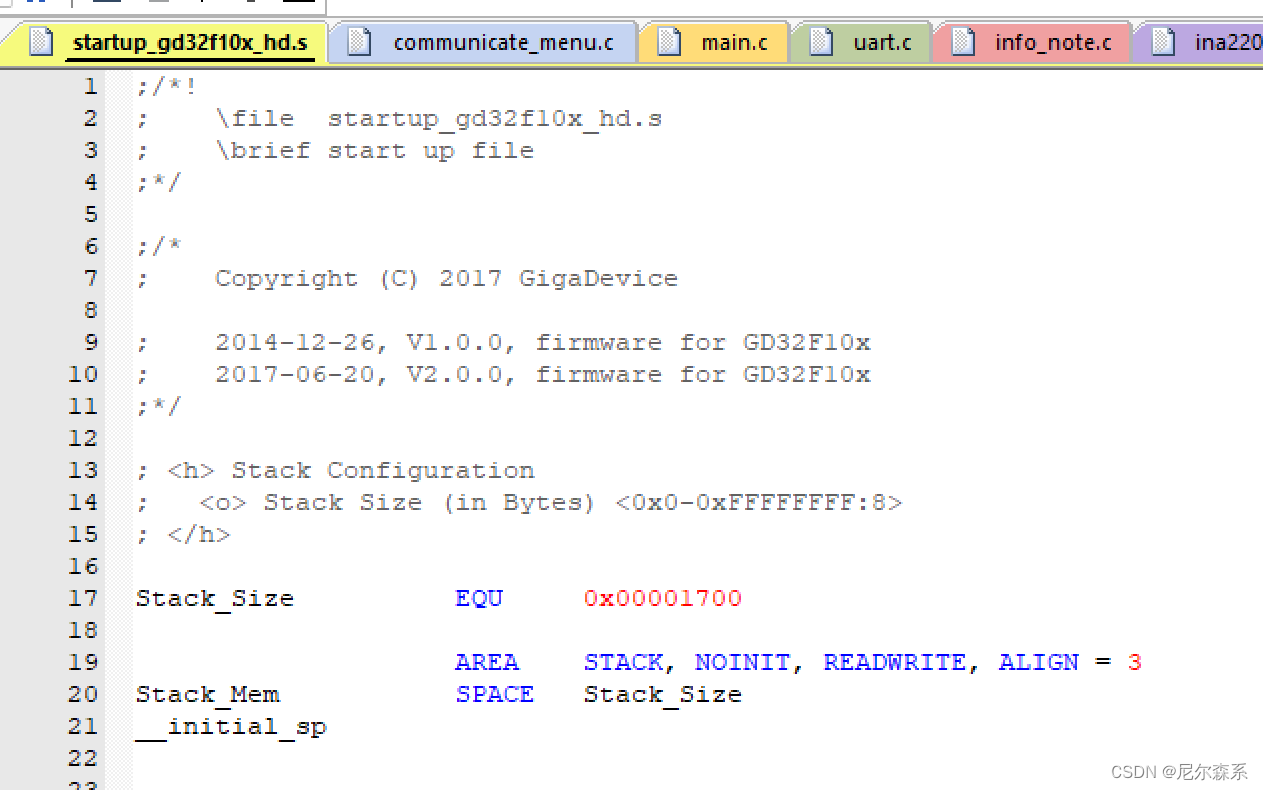
FreeRTOS实时系统 在任务中增加数组等相关操作 导致单片机起不来或者挂掉
在调试串口任务中增加如下代码,发现可以用keil进行仿真,但是烧录程序后,调试串口没有打印,状态灯也不闪烁,单片机完全起不来 博主就纳了闷了,究竟是什么原因,这段代码可是公司永流传的老代码了&…...

CentOS 7基础操作08_Linux查找目录和文件
1、which命令——查找用户所执行的命令文件存放的目录 which命令用于查找Linux命令程序并显示所在的具体位置.其搜索范围主要由用户的环境变量PATH决定(可以执行言echo sPATH”命令查看),这个范围也是Linux操作系统在执行命令或程序时的默认搜索路径。 which命令使用要查找的命…...

CI/CD实战面试宝典:从构建到高可用性的全面解析
实战部署与配置 请描述你设计和实现的一个CI/CD pipeline的完整流程,包括构建、测试、部署各个阶段。 我设计的CI/CD pipeline通常包括以下几个阶段: 代码提交:开发人员将代码提交到Git仓库,触发CI/CD流程。代码检查࿱…...
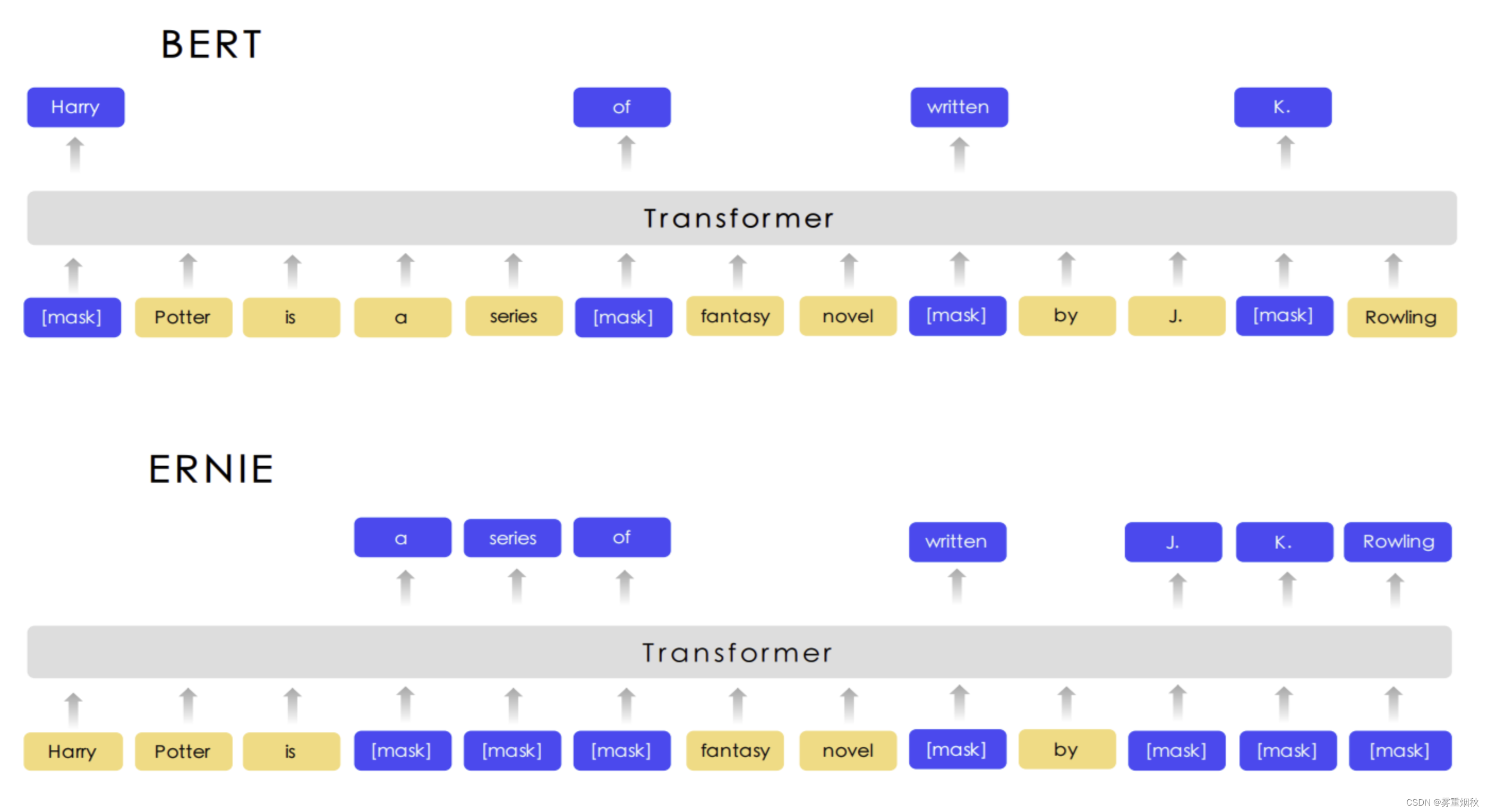
NLP实战入门——文本分类任务(TextRNN,TextCNN,TextRNN_Att,TextRCNN,FastText,DPCNN,BERT,ERNIE)
本文参考自https://github.com/649453932/Chinese-Text-Classification-Pytorch?tabreadme-ov-file,https://github.com/leerumor/nlp_tutorial?tabreadme-ov-file,https://zhuanlan.zhihu.com/p/73176084,是为了进行NLP的一些典型模型的总…...
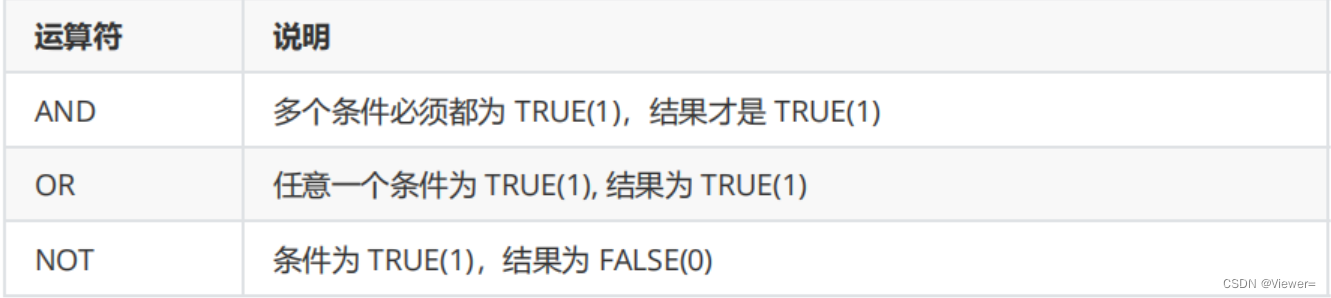
MySQL: 表的增删改查(基础)
文章目录 1. 注释2. 新增(Create)3. 查询(Retrieve)3.1 全列查询3.2 指定列查询3.3 查询字段为表达式3.4 别名3.5 去重: distinct3.6 排序: order by3.7条件查询3.8 分页查询 4. 修改 (update)5. 删除(delete)6. 内容重点总结 1. 注释 注释:在SQL中可以使用“–空格…...
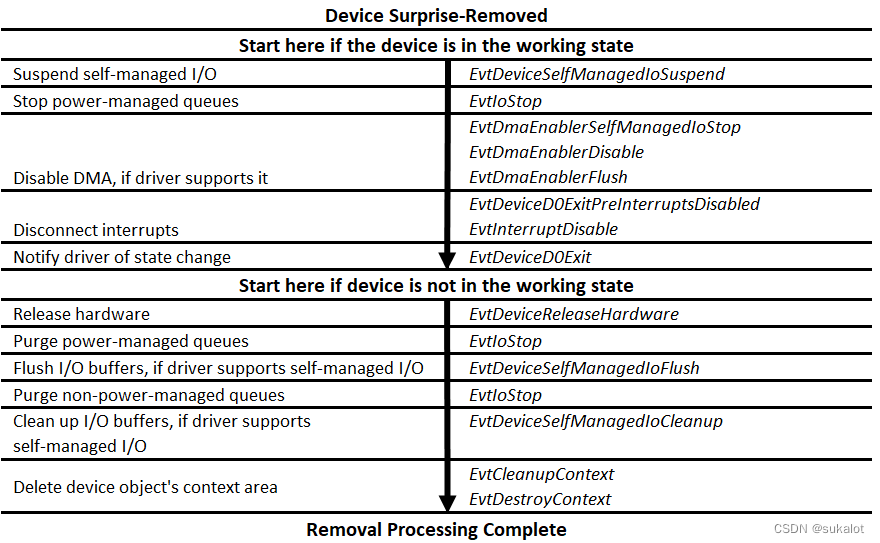
WDF驱动开发-PNP和电源管理(三)
对于PNP设备来说,理解它们的启动和删除顺序,以及意外移除顺序非常重要,在早期,经常有拔插U盘导致windows重启的例子,这就是意外移除带来的问题。 功能或Filter驱动程序的启动顺序 下图显示了框架调用 WDF (KMDF 和 U…...

Redis集群和高可用性:保障Redis服务的稳定性
I. 引言 A. 对Redis的简单介绍和其在现代Web应用中的角色 Redis(REmote DIctionary Server)是一个开源的、基于内存的键值数据库,它支持多种数据结构,如字符串、哈希、列表、集合、有序集合等。由于Redis的高性能和丰富的数据类型,使其在现代Web应用中广泛使用。例如,它…...
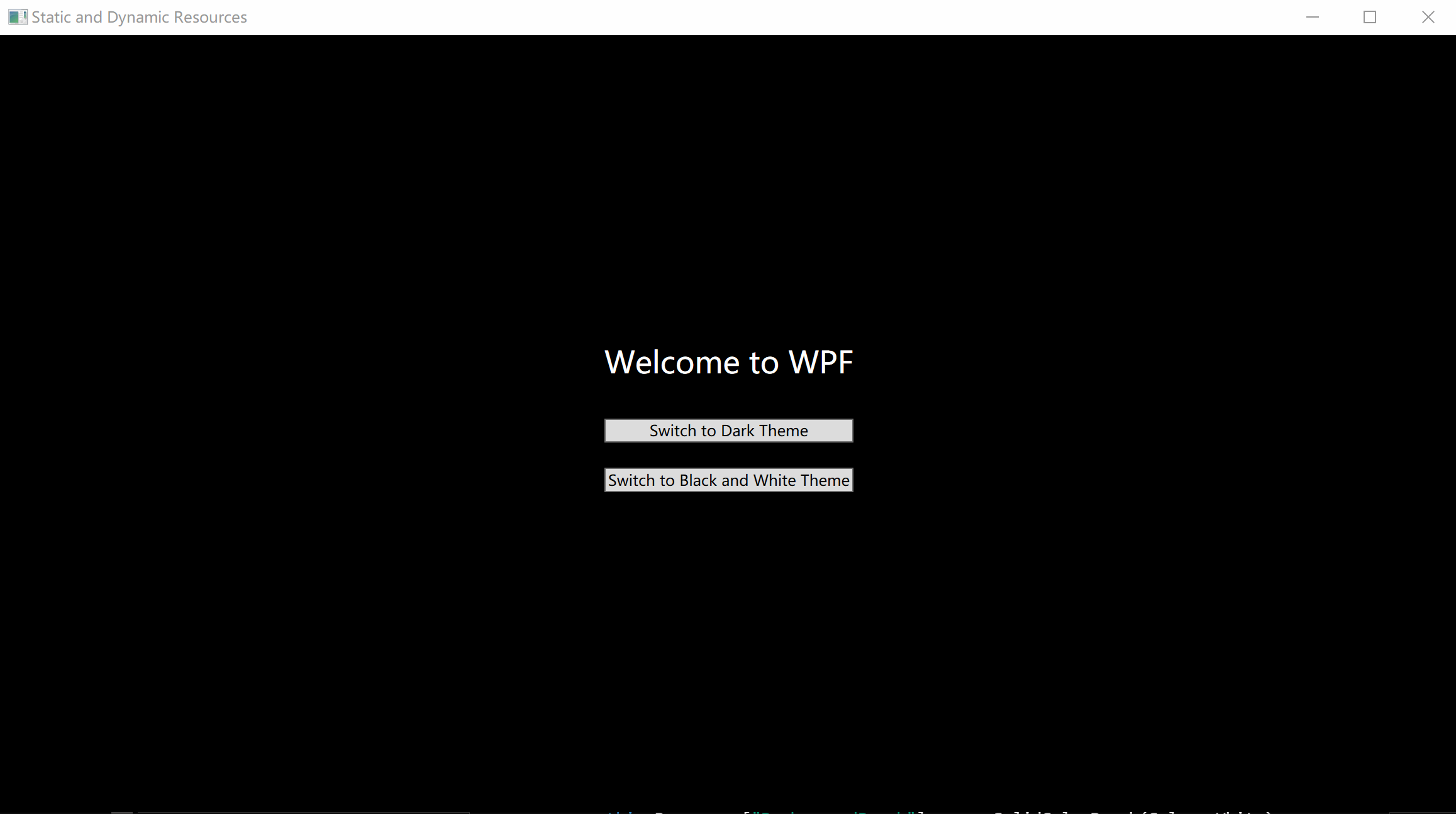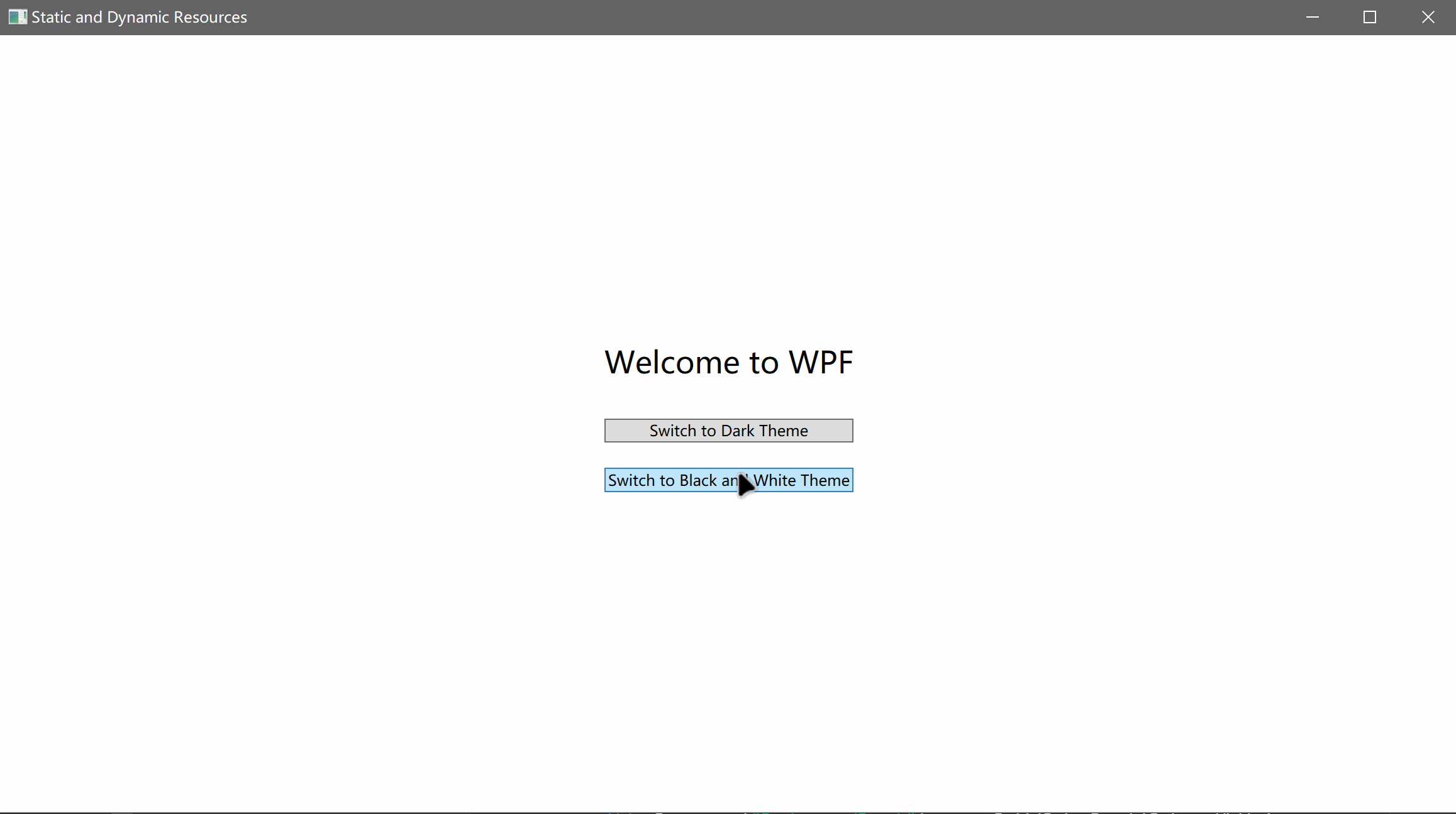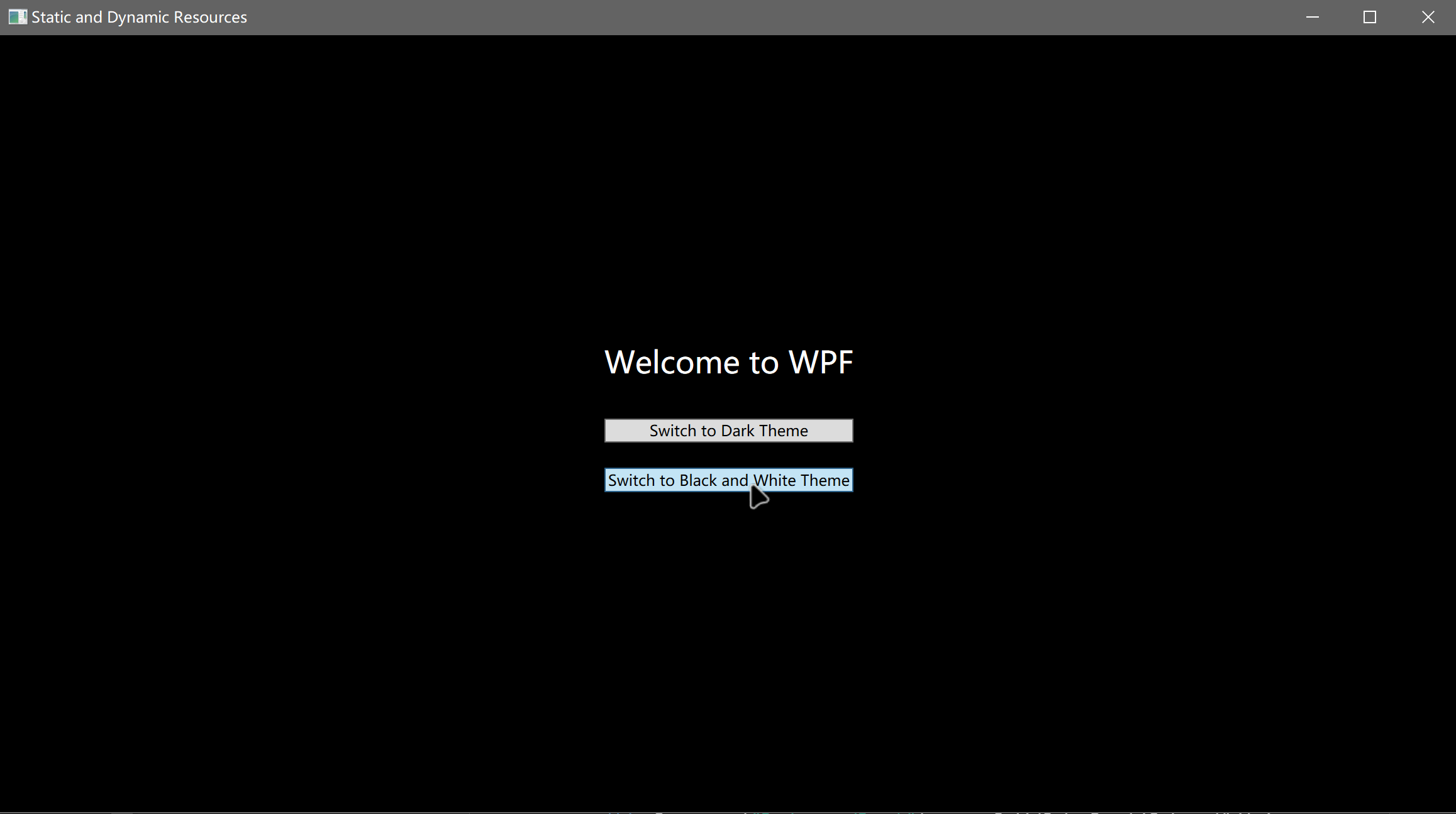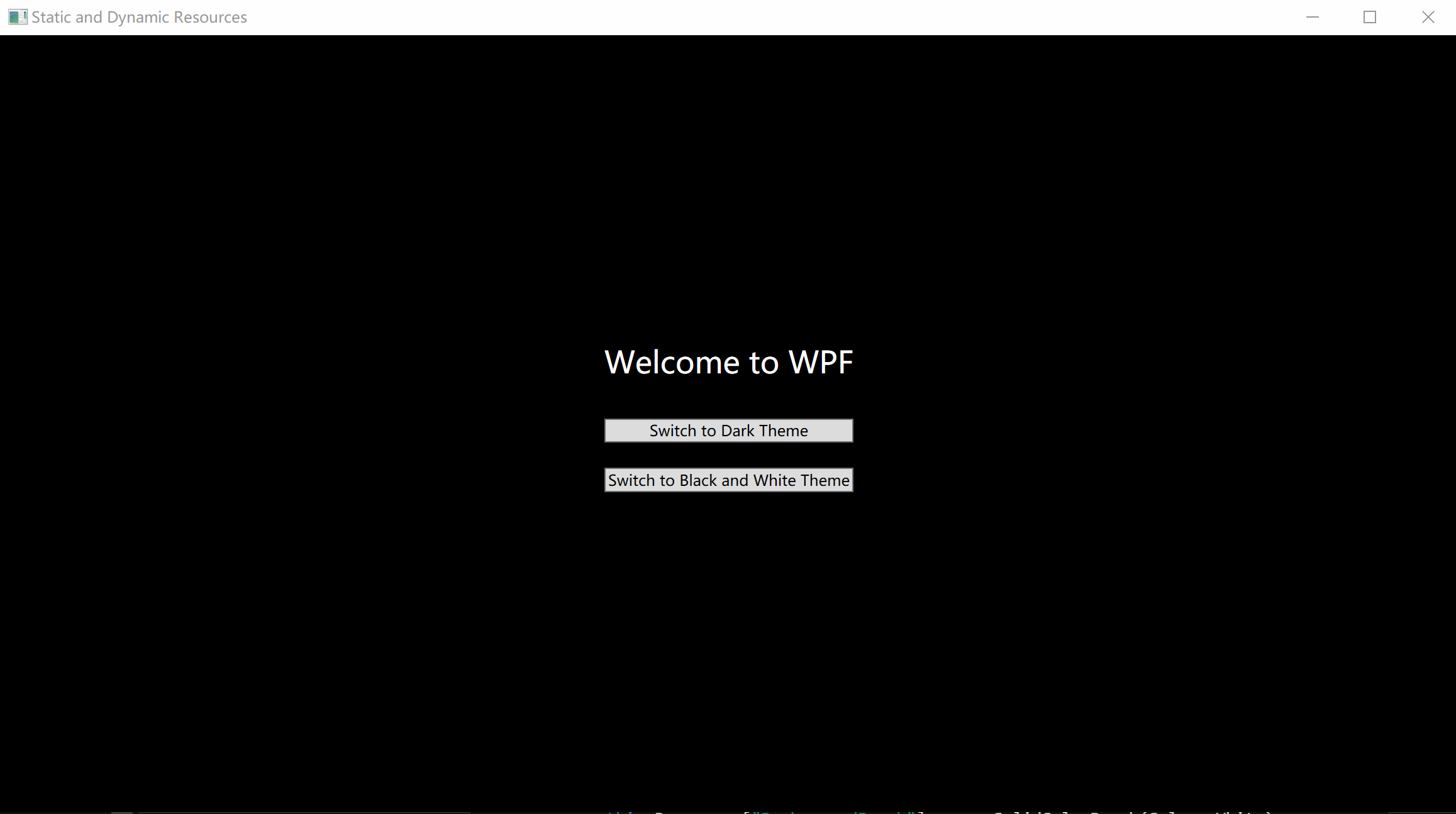
C# WPF入门学习主线篇(二十一)—— 静态资源和动态资源
C# WPF入门学习主线篇(二十一)—— 静态资源和动态资源 欢迎来到C# WPF入门学习系列的第二十一篇。在上一章中,我们介绍了WPF中的资源和样式。本篇文章将深入探讨静态资源(StaticResource)和动态资源(Dynam…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
