GAN的入门理解
这一篇主要是关于生成对抗网络的模型笔记,有一些简单的证明和原理,是根据李宏毅老师的课程整理的,下面有链接。本篇文章主要就是梳理基础的概念和训练过程,如果有什么问题的话也可以指出的。
李宏毅老师的课程链接
1.概述
GAN是Generative Adversarial Networks的缩写,也就是生成对抗网络,最核心在于训练两个网络分别是generator和discriminator,generator主要是输入一个向量,输出要生成的目标,discriminator接受一个输出的目标,然后输出为真的概率(来说就是打分)。
假设任务是生成一组图片,现在输入是一组图片数据集,一开始随便生成乱七八糟的数据,训练共有两个核心的步骤:
- 更新discriminator,将真实数据标记为1,生成的数据标记为0,然后进行训练,那么discrimator就可以辨别生成图片。
- 更新generator,更新生成网络的参数,让生成网络生成的图片能让discriminator输出尽可能大(打分尽可能高,也就是骗过discriminator)。
- 回到1,重复这个过程。
下面是最原始的论文提出的伪代码:

可以看到第一个阶段是在更新discriminator,D(x)表示对输入图像x的判别,损失函数是两项累加,前面的 x i x^i xi表示真实输入,这些应该输出1,后面的 x ~ i \widetilde{x}^i x i表示生成数据,这些应该给低分(接近0),两项的目标都是越大越好,所以 V ~ \widetilde{V} V 越大越好,因此 θ d \theta_d θd是梯度上升优化。
第二阶段在更新generator, G ( z i ) G(z^i) G(zi)就是对一个向量生成一个目标,然后进行打分,也是越大越好,因此梯度上升优化,这一部分的目标就是让生成的图片尽量得高分。
循环多次迭代就可以得到预期网络。
当然目前我还有一些疑问:
-
generator输出的图片是如何保证风格和数据集类似的?
应该是必须要像原风格一样的才能得到高分。
-
输入的向量是随机的,如何可控输入向量和输出特征的关系?如何解释每个输入的数字?(比如我想生成蓝色的头发,那么这个是可控的吗)
这个可能要看了一些具体的代码才能理解。
2.原理简单分析
生成一个图片或者一个语音本质是映射到一个高维点的问题,比如32×32的黑白图片就是 2 32 × 32 2^{32\times 32} 232×32空间中的一个点。下面都以图片生成任务为例,假设真实分布是 P d a t a P_{data} Pdata,生成的分布是 P G P_{G} PG,只有生成的点(图片)到了真实的分布中,才有极大可能是看上去真实的,因此目标就是让生成的分布 P G P_G PG尽可能接近真实的分布 P d a t a P_{data} Pdata,方法就是KL散度或者JS散度,因此一个理想的生成器应该是这样的:
G ∗ = a r g min G D i v ( P G , P d a t a ) G^*=arg\min_G Div(P_G,P_{data}) G∗=argGminDiv(PG,Pdata)其中Div衡量两个分布的差异,而 G ∗ G^* G∗就是所有生成器 G G G中有着最小差异的那个,也就是最优的。
然而,实际情况中,真实的分布和实际的分布都是未知的,一些传统的算法可能假设高斯分布,但是很多时候可能不正确。
虽然不能直接得到分布,但是可以进行采样(Sample),在GAN中,discriminator就扮演了计算两个分布差异的角色,给出下式:
V ( G , D ) = E x ∼ P d a t a l o g ( D ( x ) ) + E x ∼ P G l o g ( 1 − D ( x ) ) V(G,D)=E_{x\sim P_{data}}log(D(x))+E_{x\sim P_{G}}log(1-D(x)) V(G,D)=Ex∼Pdatalog(D(x))+Ex∼PGlog(1−D(x))其中 D ( x ) D(x) D(x)表示一个discriminator对一个generator生成的结果进行打分,介于 [ 0 , 1 ] [0,1] [0,1],下面证明这个式子本质上也是JS散度或者KL散度:
证明:
max E x ∼ P d a t a l o g ( D ( x ) ) + E x ∼ P G l o g ( 1 − D ( x ) ) = max ∫ x p d a t a ( x ) l o g ( D ( x ) ) + ∫ x p G ( x ) l o g ( 1 − D ( x ) ) = max ∫ x p d a t a ( x ) l o g ( D ( x ) ) + p G ( x ) l o g ( 1 − D ( x ) ) \max E_{x\sim P_{data}}log(D(x))+E_{x\sim P_{G}}log(1-D(x))\\ =\max \int_xp_{data}(x)log(D(x))+\int_xp_{G}(x)log(1-D(x))\\ =\max \int_xp_{data}(x)log(D(x))+p_{G}(x)log(1-D(x)) maxEx∼Pdatalog(D(x))+Ex∼PGlog(1−D(x))=max∫xpdata(x)log(D(x))+∫xpG(x)log(1−D(x))=max∫xpdata(x)log(D(x))+pG(x)log(1−D(x))
这里假设D(x)可以拟合任何函数,那么对于任意一个x取值 x ∗ x^* x∗, D ( x ∗ ) D(x^*) D(x∗)都可以对应任何数值,这就意味着可以对每个x都计算最大值,然后求和得到最大值。
设 a = p d a t a ( x ) , b = p G ( x ) , D ( x ) = t a=p_{data}(x),b=p_G(x),D(x)=t a=pdata(x),b=pG(x),D(x)=t,那么可以得到下式:
f ( t ) = a l o g ( t ) + b l o g ( 1 − t ) f(t)=alog(t)+blog(1-t) f(t)=alog(t)+blog(1−t)求导计算最小值对应的t:(直接假设e为底了)
f ′ ( t ) = a x − b 1 − x f'(t)=\frac{a}{x}-\frac{b}{1-x} f′(t)=xa−1−xb
令 f ′ ( t ) = 0 f'(t)=0 f′(t)=0,得到 t = a a + b t=\frac{a}{a+b} t=a+ba,代入 a , b , t a,b,t a,b,t,假设这个值为最优值 D ∗ ( x ) D^*(x) D∗(x):
D ∗ ( x ) = p d a t a ( x ) p d a t a ( x ) + p G ( x ) D^*(x)=\frac{p_{data}(x)}{p_{data}(x)+p_G(x)} D∗(x)=pdata(x)+pG(x)pdata(x)此时每个x都有对应的 D ∗ ( x ) D^*(x) D∗(x),代入得到:
max ∫ x p d a t a ( x ) l o g ( D ( x ) ) + p G ( x ) l o g ( 1 − D ( x ) ) = ∫ x p d a t a ( x ) l o g ( D ∗ ( x ) ) + p G ( x ) l o g ( 1 − D ∗ ( x ) ) = ∫ x p d a t a ( x ) l o g ( p d a t a ( x ) p d a t a ( x ) + p G ( x ) ) + p G ( x ) l o g ( p G ( x ) p d a t a ( x ) + p G ( x ) ) = − 2 l o g 2 + ∫ x p d a t a ( x ) l o g ( p d a t a ( x ) ( p d a t a ( x ) + p G ( x ) ) / 2 ) + p G ( x ) l o g ( p G ( x ) ( p d a t a ( x ) + p G ( x ) ) / 2 ) = − 2 l o g 2 + K L ( P d a t a ∣ ∣ P d a t a + P G 2 ) + K L ( P G ∣ ∣ P d a t a + P G 2 ) = − 2 l o g 2 + J S D ( P d a t a ∣ ∣ P G ) \max\int_xp_{data}(x)log(D(x))+p_{G}(x)log(1-D(x))\\ =\int_xp_{data}(x)log(D^*(x))+p_{G}(x)log(1-D^*(x))\\ =\int_xp_{data}(x)log(\frac{p_{data}(x)}{p_{data}(x)+p_G(x)})+p_{G}(x)log(\frac{p_{G}(x)}{p_{data}(x)+p_G(x)})\\ =-2log2+\int_xp_{data}(x)log(\frac{p_{data}(x)}{(p_{data}(x)+p_G(x))/2})+p_{G}(x)log(\frac{p_{G}(x)}{(p_{data}(x)+p_G(x))/2})\\ =-2log2+KL(P_{data}||\frac{P_{data}+P_G}{2})+KL(P_{G}||\frac{P_{data}+P_G}{2})\\ =-2log2+JSD(P_{data}||P_G) max∫xpdata(x)log(D(x))+pG(x)log(1−D(x))=∫xpdata(x)log(D∗(x))+pG(x)log(1−D∗(x))=∫xpdata(x)log(pdata(x)+pG(x)pdata(x))+pG(x)log(pdata(x)+pG(x)pG(x))=−2log2+∫xpdata(x)log((pdata(x)+pG(x))/2pdata(x))+pG(x)log((pdata(x)+pG(x))/2pG(x))=−2log2+KL(Pdata∣∣2Pdata+PG)+KL(PG∣∣2Pdata+PG)=−2log2+JSD(Pdata∣∣PG)
后面的几步其实不是很理解,不过到第三步,跟交叉熵形式很像,所以都是类似的衡量两个分布的差异。
训练一个discriminator,实际上就是为了更好区分真实和生成的样本,那么自然要让这个差异越大越好,此时这个discriminator可以最大程度区分生成和真实。 D ∗ D^* D∗给的打分实际上可以看做生成分布和实际分布的差异。
D ∗ = a r g max D V ( G , D ) D^*=arg\max_D V(G,D) D∗=argDmaxV(G,D)而训练generator的过程就是为了让discriminator不容易区分真实和生成样本,因此要减少这个差异:
D ∗ = a r g min G V ( G , D ∗ ) = a r g min G max D V ( G , D ) D^*=arg\min_G V(G,D^*) =arg\min_G \max_D V(G,D) D∗=argGminV(G,D∗)=argGminDmaxV(G,D)
也就是现在有一个最优的discriminator D ∗ D^* D∗,要优化generator使得 D ∗ D^* D∗打分尽量高,也就是:
θ g = θ g − η ∂ V ( G , D ∗ ) θ g \theta_g=\theta_g-\eta \frac{\partial V(G,D^*)}{\theta_g} θg=θg−ηθg∂V(G,D∗)这里实际上是对 θ G \theta_G θG也就是生成网络的参数求导,实际的网络架构是: v e c t o r → θ G → o u t → θ D → s c o r e vector\rightarrow \theta_G \rightarrow out \rightarrow \theta_D \rightarrow score vector→θG→out→θD→score,这里更新的时候,不更新 θ D \theta_D θD,这也就是固定discriminator的思想。
注意点:每次更新的时候,对discriminator的更新要彻底,对generator的更新次数不能多,如下图:
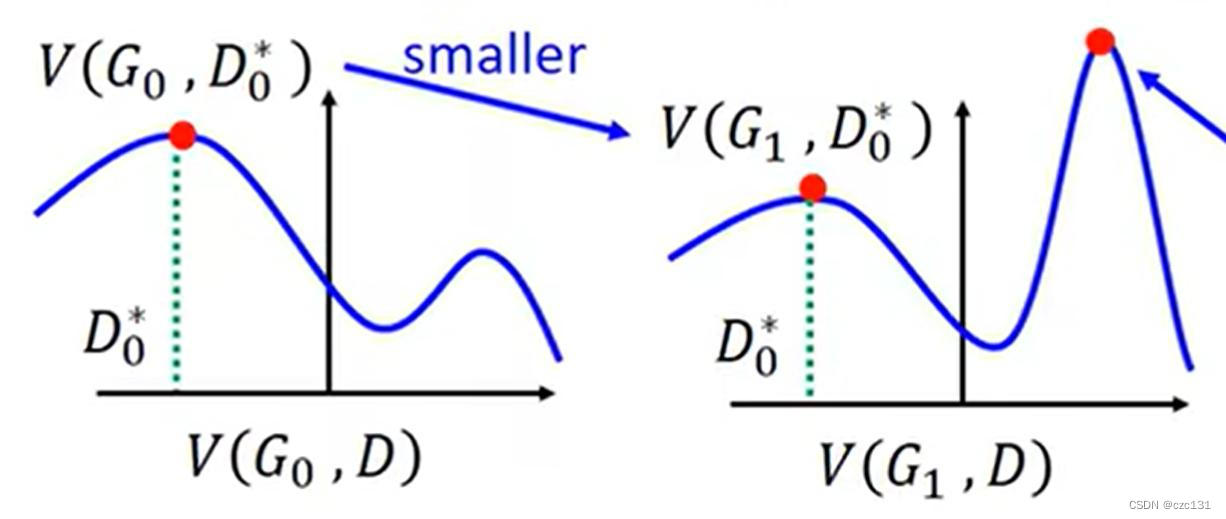
比如现在训练了一个discriminator是 D 0 ∗ D^*_0 D0∗,现在要让G变得更强,也就是让 D 0 ∗ D^*_0 D0∗对G生成的图辨别能力降低,直观体现就是 V ( G , D ) V(G,D) V(G,D)变小,但是因为更新参数对生成分布的影响是全局的,那么就可能导致生成图片和实际分布差异变得更大,因为变小的只有 D 0 ∗ D^*_0 D0∗的得分,可能这时候 D 0 ∗ D^*_0 D0∗已经不是最好的discriminator,而更好的discriminator可以将生成的和实际的分的更开,就像图二的最大值必原来的还大,那么对应于更高的 D ∗ D^* D∗计算得到的差异比原来还大。(有点绕这里)
所以有一个简单的假设,就是generator更新后的图形基本和原来保持一致,那么此时优化最大值让最大值变小,那么就相当于生成分布和实际分布差异更小,要达到这样的目的,那么不能更新generator太多;而对于discriminator,因为要找到最大值,应该要更新彻底。
3.实际操作
上面都是理论上的分析,下面讲一讲在实际的操作中是怎么做的。
3.1.训练discriminator
一个discriminator其实就是一个二分分类器,输入一个生成的数据,给出为真的概率,所以训练的过程也是和训练分类器是一样的,上面提到了 V ( G , D ) V(G,D) V(G,D)优化目标,里面有期望,期望一般会被转化为求多个样本的均值来获得。对于一个确定的生成器G,假设抽样取得m个真实样本X,生成了m个生成样本X’,那么期望可以转化为:
V ( D ) = E x ∼ P d a t a l o g ( D ( x ) ) + E x ∼ P G l o g ( 1 − D ( x ) ) = > V ~ = 1 m ∑ i = 1 m l o g ( D ( x i ) ) + 1 m ∑ i = 1 m l o g ( 1 − D ( x i ′ ) ) V(D)=E_{x\sim P_{data}}log(D(x))+E_{x\sim P_{G}}log(1-D(x))\\ =>\widetilde{V}=\frac{1}{m}\sum_{i=1}^{m}log(D(x_i))+\frac{1}{m}\sum_{i=1}^{m}log(1-D(x'_i)) V(D)=Ex∼Pdatalog(D(x))+Ex∼PGlog(1−D(x))=>V =m1i=1∑mlog(D(xi))+m1i=1∑mlog(1−D(xi′))
一般会采用梯度上升法:(因为要求最大值)
θ d = θ d + η ▽ θ d V ~ ( θ d ) \theta_d=\theta_d+\eta ▽_{\theta_d}\widetilde{V}(\theta_d) θd=θd+η▽θdV (θd)
3.2.训练generator
训练generator实际上是为了减少 V ( G , D ∗ ) V(G,D^*) V(G,D∗),也就是让目前最好的分类器分不清,还是抽样,生成n个样本X’,那么目标如下:
V ( D ) = 1 m ∑ i = 1 m l o g ( 1 − D ( G ( x i ′ ) ) ) V(D)=\frac{1}{m}\sum_{i=1}^{m}log(1-D(G(x'_i))) V(D)=m1i=1∑mlog(1−D(G(xi′)))此时在变的是gegenerator的参数 θ g \theta_g θg,要通过改变生成参数让最好的discriminator得分降低,一般是梯度下降:
θ g = θ g − η ▽ θ g V ~ ( θ g ) \theta_g=\theta_g-\eta ▽_{\theta_g}\widetilde{V}(\theta_g) θg=θg−η▽θgV (θg)要注意,不能训练次数太多(一般一次就可以)。
具体的代码实现我还没有去看过,就不进一步展开了,这一篇主要还是记录一些简单的原理。
相关文章:

GAN的入门理解
这一篇主要是关于生成对抗网络的模型笔记,有一些简单的证明和原理,是根据李宏毅老师的课程整理的,下面有链接。本篇文章主要就是梳理基础的概念和训练过程,如果有什么问题的话也可以指出的。 李宏毅老师的课程链接 1.概述 GAN是…...

43【PS 作图】颜色速途
1 通过PS让画面细节模糊,避免被过多的颜色干扰 2 分析画面的颜色 3 作图 参考网站: 色感不好要怎么提升呢?分享一下我是怎么练习色感的!_哔哩哔哩_bilibili https://www.bilibili.com/video/BV1h1421Z76p/?spm_id_from333.1007.…...

定个小目标之刷LeetCode热题(13)
今天来看看这道题,介绍两种解法 第一种动态规划,代码如下 class Solution {public int maxSubArray(int[] nums) {int pre 0, maxAns nums[0];for (int x : nums) {// 计算当前最大前缀和pre Math.max(pre x, x);// 更新最大前缀和maxAns Math.ma…...
【AI大模型】Prompt Engineering
目录 什么是提示工程(Prompt Engineering) Prompt 调优 Prompt 的典型构成 「定义角色」为什么有效? 防止 Prompt 攻击 攻击方式 1:著名的「奶奶漏洞」 攻击方式 2:Prompt 注入 防范措施 1:Prompt 注…...
centos安装vscode的教程
centos安装vscode的教程 步骤一:打开vscode官网找到历史版本 历史版本链接 步骤二:找到文件下载的位置 在命令行中输入(稍等片刻即可打开): /usr/share/code/bin/code关闭vscode后,可在应用程序----编程…...

面试题------>MySQL!!!
一、连接查询 ①:左连接left join (小表在左,大表在右) ②:右连接right join(小表在右,大表在左) 二、聚合函数 SQL 中提供的聚合函数可以用来统计、求和、求最值等等 COUNT&…...

英伟达:史上最牛一笔天使投资
200万美元的天使投资,让刚成立就面临倒闭风险的英伟达由危转安,并由此缔造了一个2.8万亿美元的市值神话。 这是全球风投史上浓墨重彩的一笔。 前不久,黄仁勋在母校斯坦福大学的演讲中,提到了人生中的第一笔融资——1993年&#x…...

PDF分页处理:技术与实践
引言 在数字化办公和学习中,PDF文件因其便携性和格式稳定性而广受欢迎。然而,处理大型PDF文件时,我们经常需要将其拆分成单独的页面,以便于管理和分享。本文将探讨如何使用Python编程语言和一些流行的库来实现PDF文件的分页处理。…...
数据可视化——pyecharts库绘图
目录 官方文档 使用说明: 点击基本图表 可以点击你想要的图表 安装: 一些例图: 柱状图: 效果: 折线图: 效果: 环形图: 效果: 南丁格尔图(玫瑰图&am…...

Python的return和yield,哪个是你的菜?
目录 1、return基础介绍 📚 1.1 return用途:数据返回 1.2 return执行:函数终止 1.3 return深入:无返回值情况 2、yield核心概念 🍇 2.1 yield与迭代器 2.2 生成器函数构建 2.3 yield的暂停与续行特性 3、retur…...
)
持续总结中!2024年面试必问 20 道分布式、微服务面试题(七)
上一篇地址:持续总结中!2024年面试必问 20 道分布式、微服务面试题(六)-CSDN博客 十三、请解释什么是服务网格(Service Mesh)? 服务网格(Service Mesh)是一种用于处理服…...

AJAX 跨域
这里写目录标题 同源策略JSONPJSONP 是怎么工作的JSONP 的使用原生JSONP实践CORS 同源策略 同源: 协议、域名、端口号 必须完全相同、 当然网页的URL和AJAX请求的目标资源的URL两者之间的协议、域名、端口号必须完全相同。 AJAX是默认遵循同源策略的,不…...

3 数据类型、运算符与表达式-3.1 C语言的数据类型和3.2 常量与变量
数据类型 基本类型 整型字符型实型(浮点型) 单精度型双精度型 枚举类型 构造类型 数组类型结构体类型共用体类型 指针类型空类型 #include <stdio.h> #include <string.h> #include <stdbool.h> // 包含布尔类型定义 // 常量和符号常量 #define PRICE 30//…...
NSSCTF-Web题目5
目录 [SWPUCTF 2021 新生赛]error 1、题目 2、知识点 3、思路 [LitCTF 2023]作业管理系统 1、题目 2、知识点 3、思路 [HUBUCTF 2022 新生赛]checkin 1、题目 2、知识点 3、思路 [SWPUCTF 2021 新生赛]error 1、题目 2、知识点 数据库注入、报错注入 3、思路 首先…...

cnvd_2015_07557-redis未授权访问rce漏洞复现-vulfocus复现
1.复现环境与工具 环境是在vulfocus上面 工具:GitHub - vulhub/redis-rogue-getshell: redis 4.x/5.x master/slave getshell module 参考攻击使用方式与原理:https://vulhub.org/#/environments/redis/4-unacc/ 2.复现 需要一个外网的服务器做&…...

免费,C++蓝桥杯等级考试真题--第7级(含答案解析和代码)
C蓝桥杯等级考试真题--第7级 答案:D 解析:步骤如下: 首先,--a 操作会使 a 的值减1,因此 a 变为 3。判断 a > b 即 3 > 3,此时表达式为假,因为 --a 后 a 并不大于 b。因此,程…...

python为什么要字符串格式化
Python2.6 开始,新增了一种格式化字符串的函数 str.format(),它增强了字符串格式化的功能。相对于老版的%格式方法,它有很多优点。 1.在%方法中%s只能替代字符串类型,而在format中不需要理会数据类型; 2.单个参数可以…...
go语言后端开发学习(三)——基于validator包实现接口校验
前言 在我们开发模块的时候,有一个问题是我们必须要去考虑的,它就是如何进行入参校验,在gin框架的博客中我就介绍过一些常见的参数校验,大家可以参考gin框架学习笔记(四) ——参数绑定与参数验证,而这个其实也不是能够完全应对我…...
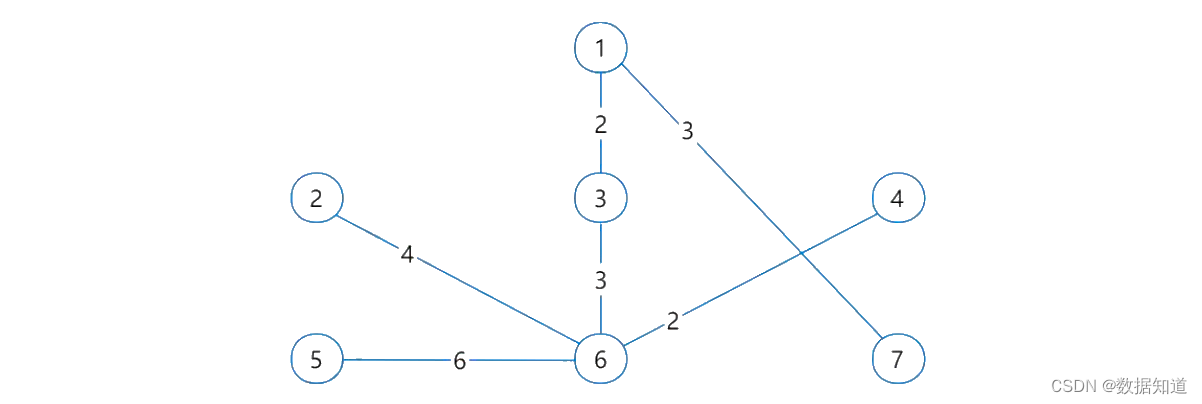
系统架构设计师【补充知识】: 应用数学 (核心总结)
一、 图论之最小生成树 (1)定义: 在连通的带权图的所有生成树中,权值和最小的那棵生成树(包含图中所有顶点的树),称作最小生成树。 (2)针对问题: 带权图的最短路径问题。 (3)最小生成树的解法有普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法,我…...
栅格数据格式)
【ArcGIS微课1000例】0118:一文讲清楚tif(geotiff)栅格数据格式
文章目录 一、Tiff概述二、GeoTiff概述1. ovr文件2. tfw文件3. xml文件4. dbf文件一、Tiff概述 TIFF(Tagged Image File Format)是一种常见的图像文件格式,它被广泛用于存储和传输各种类型的图像数据。下面是对TIFF格式数据的介绍: 图像存储:TIFF格式可以存储多通道的位…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...
