让GNSSRTK不再难【第二天-第4部分】
第12讲 GNSS授时与PPS
12.1 为什么需要高精度时间
授时的传统理解就是时间传递或者对时。比如以前手机没这么方便时,大家还都使用石英钟手表看时间时,大家都习惯晚上七点准时对着中央一套的报时,来校准你家的机械钟或者挂钟,这就是最简单的时间传递,这种时间传递的精度,秒的量级,对于日常生活已经足够。
但是全世界这么多表,如何将大家的时间都统一起来呢。以前的笨方法以及现在还在使用的方法就是,大家都把表放到一块,一块对比校准一下不就可以做到统一了嘛。但是全世界这么多设备,如何大家统一呢。像电视,就是时间传递的一种,其他的还有电话、电波授时等。
但是此类的授时,精度都相对较低,但有些场景我们又要比较高的时间精度。比如两个摄像头拍摄的画面,如果每个摄像头同1s内拍摄了10000张图片,如果我们要将两个设备拍摄的图像拼接起来,那么两个设备的时间相差要在1/10000秒以下,这样我们才能对齐指定的画面。在我们传统的电力、移动通信等行业,有些时间的精度要在纳秒量级,也就是一亿分之一秒。
在分布式系统中,由于物理上的分散性,系统无法为彼此间相互独立的模块提供一个统一的全局时钟,而由各个进程或模块各自维护它们的本地时钟。由于这些本地时钟的计时速率、运行环境存在不一致性,因此即使所有本地时钟在某一时刻都被校准,一段时间后,这些本地时钟也会出现不一致。为了这些本地时钟再次达到相同的时间值,必须进行时间同步操作。授时技术又是实现时间同步的重要技术手段。
精密时间是科学研究、科学实验和工程技术诸方面的基本物理参量。它为一切动力学系统和时序过程的测量和定量研究提供了必不可少的时基坐标。
精密授时在以通信、电力、控制等工业领域和国防领域有着广泛和重要的应用。现代武器实(试)验、战争需要它保障,智能化交通运输系统的建立和数字化地球的实现需要它支持。现代通信网和电力网建设也越来越增强了对精度时间和频率的依赖。从建立一个现代化国家的大系统工程总体考虑,导航定位和授时系统应该说是基础的基础。它对整体社会的支撑几乎是全方位的。
卫星发射:
火箭发射升空后,不论是发射场、测控站以及测量船都会对火箭进行连续测控。而所有的测控都会根据火箭的飞行轨迹和速度,推算出火箭将出现的方位和时间。这时候如果各个测控站的时间不同步,就有极大的可能追踪火箭失败。
航天活动:
平常在电影中或者新闻里都会看到飞船和目标飞行器交会对接的画面。就像是我国“天舟一号”以及“天宫二号”的交会对接,都是需要精密的时间同步,对两个飞行器进行姿态的同步观测,实时发出测控指令,才能保证对接成功,否则,“太空之吻”的美谈就很有可能变为“太空车祸”。
金融领域:
现代金融行业,无论银行或证券交易所,都离不开计算机和计算机联网,单个计算机业务和计算机联网业务,如银行业务往来的发生时刻、金融交易的准确时刻、E-mail 信息和访问时间、数据库处理时间、银联卡/账户的密码识别等等,都涉及银行联网计算机之间的时间同步和频率同步,都需要精准授时。
电力系统:
对于电力系统而言,每一条由电厂汇入总干线的电流在同一时刻具有不同的相位。为让各电厂在每一时刻输送的电流按照预定的相位,而不至于发生在本该送入波峰而送入反向的波谷导致短路等情况,电网整体的工作协调需要一个全局统一的时钟完成。而电网的时钟同步正是由本文的标题,”GPS秒脉冲达成时间同步“来完成。
12.2 授时原理
12.2.1 卫星单向法
使用GNSS系统进行高精度授时的原理其实已经呼之欲出,我们前面提到的解算结果接收机钟差,其实就是本地时钟与GNSS时间框架的差异。
单向法的误差来源是卫星位置与星历的偏差、电离层层扰动以及接收设备误差等。能接收到多颗卫星信号,并进行长时间平均的十分理想的情况下,该方法可以达到接近1ns左右的时标同步精度。
一般来说,对已知精密坐标的固定用户,观测1颗卫星,就可以实现精密的时间测量或者同步。若观测2颗卫星或者更多卫星,则提供了更多的观测量,提高了定时的稳健性。
12.2.2 卫星共视法
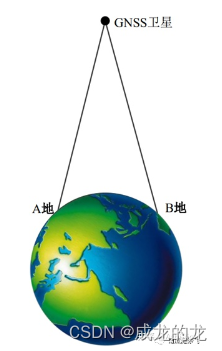
两个地面站A和B同时观测一枚GNSS卫星,通过一定的同时观测时间安排,并通过网络传输进行对比,也可以实现授时。
12.3 高精度时间传递-PPS
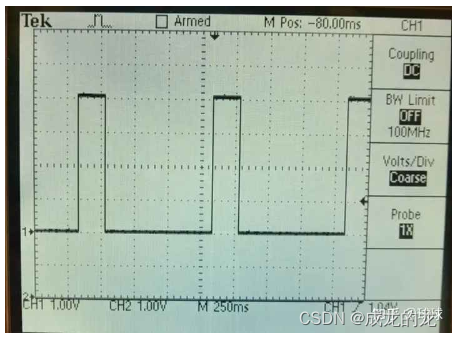
PPS:秒脉冲(Pulse Per Second)
形式化定义:GPS接收模块(GPS Receiver)可以产生秒脉冲信号,其作用是指示整秒的时间间隔,并通过PPS的上升沿标示GPS给出的UTC(Coordinated Universal Time)时间对应的具体时刻。其指示整秒时间精度可达数十纳秒级,无累积误差。每秒产生的该PPS与其给出的整秒时刻可以用于晶振精确调频⸺时钟同步。
GPS秒脉冲信号 pps 一秒钟一个,它的作用是用来指示整秒的时刻,而该时刻通常是用PPS秒脉冲的上升沿来标示。因为GPS可以给出UTC时间,但用户收到时是会有延时的,那么为了精确授时,引入PPS信号上升沿来标示UTC的整秒时刻,精度可以到纳秒级,而且没有累积误差。
第13讲 仿距差分定位原理-站间单差
从单点定位的定位流程中,我们了解到卫星的轨道、钟差以及大气都存在误差,这是导致单点定位精度不佳的原因。所以我们再次列出伪距的观测值表达式。
P r , i s = ρ r , i s − c δ t s + c δ t r , i + I r , i s + T r , i s + d r , i s − d i s + ϵ P P_{r,i}^{s} = \rho_{r,i}^{s} - c\delta t^{s} + c\delta t_{r,i} + I_{r,i}^{s} + T_{r,i}^{s} + d_{r,i}^{s} - d_{i}^{s} + \epsilon_{P} Pr,is=ρr,is−cδts+cδtr,i+Ir,is+Tr,is+dr,is−dis+ϵP
其中:
- P r , i s P_{r,i}^{s} Pr,is 为卫星 s s s 到接收机 r r r 的第 i i i 频点的伪距观测值
- ρ r , i s \rho_{r,i}^{s} ρr,is 为卫星 s s s天线相位中心 到接收机 r r r 天线相位中心的几何距离(真实距离)
- c δ t s c\delta t^{s} cδts 为卫星 s s s 钟误差
- c δ t r , i c\delta t_{r,i} cδtr,i 为接收机 r r r 钟误差
- I r , i s I_{r,i}^{s} Ir,is 为卫星 s s s 到接收机 r r r 的第 i i i 频点的电离层延迟(与频率有关)
- T r , i s T_{r,i}^{s} Tr,is 为卫星 s s s 到接收机 r r r 的对流层延迟(与频率无关)
- d r , i s d_{r,i}^{s} dr,is 为接收机端第 i i i 频点的伪距硬件延迟(与频率有关)
- d i s d_{i}^{s} dis 为卫星端第 i i i 频点的伪距硬件延迟(与频率有关)
- ϵ P \epsilon_{P} ϵP 为伪距观测值噪声
单位为米
如果我们有两台接收机,分别为 r 1 r_1 r1 和 r 2 r_2 r2,那么两台接收机的同时观测到卫星 s s s 同一频点,伪距观测值如下:
P r 1 s = ρ r 1 s − c δ t s + c δ t r 1 + I r 1 s + T r 1 s + d r 1 − d s + ϵ P P_{r_1}^{s} = \rho_{r_1}^{s} - c\delta t^{s} + c\delta t_{r_1} + I_{r_1}^{s} + T_{r_1}^{s} + d_{r_1} - d^{s} + \epsilon_{P} Pr1s=ρr1s−cδts+cδtr1+Ir1s+Tr1s+dr1−ds+ϵP
P r 2 s = ρ r 2 s − c δ t s + c δ t r 2 + I r 2 s + T r 2 s + d r 2 − d s + ϵ P P_{r_2}^{s} = \rho_{r_2}^{s} - c\delta t^{s} + c\delta t_{r_2} + I_{r_2}^{s} + T_{r_2}^{s} + d_{r_2} - d^{s} + \epsilon_{P} Pr2s=ρr2s−cδts+cδtr2+Ir2s+Tr2s+dr2−ds+ϵP
其中下标 r 1 r_1 r1 代表1号接收机, r 2 r_2 r2 代表2号接收机。
有关系的项:
- c δ t s c\delta t^{s} cδts 是卫星钟差,对接收机 r 1 r_1 r1 和 r 2 r_2 r2 都有相同的影响。
- ϵ P \epsilon_{P} ϵP 伪距测量噪声,同样会影响到接收机 r 1 r_1 r1 和 r 2 r_2 r2 的测量结果。
- d s d^{s} ds 是卫星硬件延迟,对接收机 r 1 r_1 r1 和 r 2 r_2 r2 都有相同的影响。
相互没关系的项:
- ρ r 1 s \rho_{r_1}^{s} ρr1s 和 ρ r 2 s \rho_{r_2}^{s} ρr2s 表示各自接收机到卫星的真实距离。
- c δ t r 1 c\delta t_{r_1} cδtr1 和 c δ t r 2 c\delta t_{r_2} cδtr2 表示各自接收机的钟差。
- I r 1 s I_{r_1}^{s} Ir1s 和 I r 2 s I_{r_2}^{s} Ir2s 表示各自接收机的电离层延迟。
- T r 1 s T_{r_1}^{s} Tr1s 和 T r 2 s T_{r_2}^{s} Tr2s 表示各自接收机的对流层延迟。
- d r 1 d_{r_1} dr1 和 d r 2 d_{r_2} dr2 表示各自接收机的硬件延迟。
13.1 大气误差以及卫星硬件延迟
如果对同一个卫星同一频率的两个接收机观测值进行作差,即站间单差:
P r 1 − r 2 s = ρ r 1 − r 2 s + c δ t r 1 − r 2 + I r 1 − r 2 s + T r 1 − r 2 s + d r 1 − r 2 s + ϵ P r 1 − r 2 P_{r_1 - r_2}^{s} = \rho_{r_1 - r_2}^{s} + c\delta t_{r_1 - r_2} + I_{r_1 - r_2}^{s} + T_{r_1 - r_2}^{s} + d_{r_1 - r_2}^{s} + \epsilon_{P_{r_1 - r_2}} Pr1−r2s=ρr1−r2s+cδtr1−r2+Ir1−r2s+Tr1−r2s+dr1−r2s+ϵPr1−r2
解释这里每一项是什么的差:
- P r 1 − r 2 s P_{r_1 - r_2}^{s} Pr1−r2s: 第 s s s 频点的站间单差伪距离测量值。表示在两个接收机(站点) r 1 r_1 r1 和 r 2 r_2 r2 之间的差分伪距测量值。
- ρ r 1 − r 2 s \rho_{r_1 - r_2}^{s} ρr1−r2s: 第 s s s 频点的站间单差真实距离。表示在两个接收机(站点) r 1 r_1 r1 和 r 2 r_2 r2 之间的真实距离差。
- c δ t r 1 − r 2 c\delta t_{r_1 - r_2} cδtr1−r2: 站间单差钟差项。表示两个接收机(站点)之间的钟差,以光速 c c c 乘以钟差 δ t r 1 − r 2 \delta t_{r_1 - r_2} δtr1−r2 表示。
- I r 1 − r 2 s I_{r_1 - r_2}^{s} Ir1−r2s: 第 s s s 频点的站间单差电离层延迟。表示两个接收机(站点)之间的电离层延迟差。
- T r 1 − r 2 s T_{r_1 - r_2}^{s} Tr1−r2s: 第 s s s 频点的站间单差对流层延迟。表示两个接收机(站点)之间的对流层延迟差。
- d r 1 − r 2 s d_{r_1 - r_2}^{s} dr1−r2s: 第 s s s 频点的站间单差硬件延迟。表示两个接收机(站点)之间的硬件延迟差。
- ϵ P r 1 − r 2 \epsilon_{P_{r_1 - r_2}} ϵPr1−r2: 伪距测量噪声。表示伪距测量过程中引入的噪声。站间单差,噪声被放大。
公式相减消除的项:
- c δ t s c\delta t^{s} cδts: 卫星钟差项,因为它对两个接收机是相同的,在作差时会被消除。
- d s d^{s} ds: 卫星硬件延迟项,同样在作差时会被消除。
因为我们卫星高度在两万公里左右,如果两个接收机距离较近(小于20km),卫星信号的传播路径十分相似,电离层和对流层延迟也基本相等。所以有:
I r 1 − r 2 s ≈ 0 I_{r_1 - r_2}^{s} \approx 0 Ir1−r2s≈0
T r 1 − r 2 s ≈ 0 T_{r_1 - r_2}^{s} \approx 0 Tr1−r2s≈0
即有:
P r 1 − r 2 s = ρ r 1 − r 2 s + c δ t r 1 − r 2 + d r 1 − r 2 s + ϵ P r 1 − r 2 P_{r_1 - r_2}^{s} = \rho_{r_1 - r_2}^{s} + c\delta t_{r_1 - r_2} + d_{r_1 - r_2}^{s} + \epsilon_{P_{r_1 - r_2}} Pr1−r2s=ρr1−r2s+cδtr1−r2+dr1−r2s+ϵPr1−r2
- ρ r 1 − r 2 s \rho_{r_1 - r_2}^{s} ρr1−r2s: 第 s s s 频点的站间单差真实距离。表示两个接收机(站点)之间的真实距离差。 这是几何距离差分项。
- c δ t r 1 − r 2 c\delta t_{r_1 - r_2} cδtr1−r2: 站间单差钟差项。表示两个接收机(站点)之间的钟差。
- d r 1 − r 2 s d_{r_1 - r_2}^{s} dr1−r2s: 第 s s s 频点的站间单差硬件延迟。表示两个接收机(站点)之间的硬件延迟差。
- ϵ P r 1 − r 2 \epsilon_{P_{r_1 - r_2}} ϵPr1−r2: 伪距测量噪声。表示伪距测量过程中引入的噪声。
13.2 轨道误差
13.2.1 单站几何距离公式
几何距离可以表示为卫星轨道和接收机位置的形式。
ρ r s = ( r ⃗ s − r ⃗ r ) ⋅ u ⃗ r s \rho_{r}^{s} = (\vec{r}^{s} - \vec{r}_{r}) \cdot \vec{u}_{r}^{s} ρrs=(rs−rr)⋅urs
[ 向量*单位向量 = 模 ]
其中,
- r ⃗ s = ( X s , Y s , Z s ) \vec{r}^{s} = (X^{s}, Y^{s}, Z^{s}) rs=(Xs,Ys,Zs) 为卫星位置向量
- r ⃗ r = ( X r , Y r , Z r ) \vec{r}_{r} = (X_{r}, Y_{r}, Z_{r}) rr=(Xr,Yr,Zr) 为接收机位置向量
- u ⃗ r s \vec{u}_{r}^{s} urs 为视线方向单位向量
从单点定位理论,我们如果只知大概路径位置,那可以通过将几何距离表示概略路径位置和位置偏差的形式。如下:
R ⃗ 0 s = ( r ⃗ s − r ⃗ 0 ) ⋅ u ⃗ r s \vec{R}_{0}^{s} = (\vec{r}^{s} - \vec{r}_{0}) \cdot \vec{u}_{r}^{s} R0s=(rs−r0)⋅urs
ρ r s = ( r ⃗ s − ( r ⃗ 0 r + d r ⃗ ) ) ⋅ u ⃗ r s = R 0 s − d r ⃗ ⋅ u ⃗ r s \rho_r^s = (\vec{r}^s - (\vec{r}_0^r + \vec{dr})) \cdot \vec{u}_r^s = R_0^s - \vec{dr} \cdot \vec{u}_r^s ρrs=(rs−(r0r+dr))⋅urs=R0s−dr⋅urs
[ 单位向量:概略位置和真实位置偏差不大,10m以内,单位向量忽略]
[ 最终表达是为:概略位置+位置偏差与单位向量的内积 ]
其中,
- r ⃗ 0 = ( X 0 , Y 0 , Z 0 ) \vec{r}_{0} = (X_{0}, Y_{0}, Z_{0}) r0=(X0,Y0,Z0) 为接收机概略位置向量
- d r ⃗ = ( d x , d y , d z ) \vec{dr} = (dx, dy, dz) dr=(dx,dy,dz) 为接收机概略位置的偏差向量
- u ⃗ r s = ( l s , m s , n s ) \vec{u}_{r}^{s} = (l^{s}, m^{s}, n^{s}) urs=(ls,ms,ns) 为方向余弦向量,其中 l s = X s − X 0 R 0 s l^{s} = \frac{X^{s} - X_{0}}{R_{0}^{s}} ls=R0sXs−X0, m s = Y s − Y 0 R 0 s m^{s} = \frac{Y^{s} - Y_{0}}{R_{0}^{s}} ms=R0sYs−Y0, n s = Z s − Z 0 R 0 s n^{s} = \frac{Z^{s} - Z_{0}}{R_{0}^{s}} ns=R0sZs−Z0
- R ⃗ 0 s \vec{R}_{0}^{s} R0s 为概略位置到卫星的几何距离
附加A:
u ⃗ r s = ( l s , m s , n s ) \vec{u}_{r}^{s} = (l^{s}, m^{s}, n^{s}) urs=(ls,ms,ns) 为方向余弦向量,表示从接收机(站点)到卫星的单位向量方向。
方向余弦向量的分量公式
方向余弦向量的三个分量 l s , m s , n s l^{s}, m^{s}, n^{s} ls,ms,ns 分别表示方向向量在三个坐标轴上的投影长度与其向量长度之比:
- l s = X s − X 0 R 0 s l^{s} = \frac{X^{s} - X_{0}}{R_{0}^{s}} ls=R0sXs−X0
- m s = Y s − Y 0 R 0 s m^{s} = \frac{Y^{s} - Y_{0}}{R_{0}^{s}} ms=R0sYs−Y0
- n s = Z s − Z 0 R 0 s n^{s} = \frac{Z^{s} - Z_{0}}{R_{0}^{s}} ns=R0sZs−Z0
其中:
- X s , Y s , Z s X^{s}, Y^{s}, Z^{s} Xs,Ys,Zs 是卫星在三维空间中的坐标。
- X 0 , Y 0 , Z 0 X_{0}, Y_{0}, Z_{0} X0,Y0,Z0 是接收机(站点)在三维空间中的坐标。
- R 0 s R_{0}^{s} R0s 是接收机(站点)到卫星的距离,表示为: R 0 s = ( X s − X 0 ) 2 + ( Y s − Y 0 ) 2 + ( Z s − Z 0 ) 2 R_{0}^{s} = \sqrt{(X^{s} - X_{0})^2 + (Y^{s} - Y_{0})^2 + (Z^{s} - Z_{0})^2} R0s=(Xs−X0)2+(Ys−Y0)2+(Zs−Z0)2。
通过这些公式,可以得到从接收机到卫星的方向余弦向量 u ⃗ r s \vec{u}_{r}^{s} urs,它表示的是单位向量方向。
附加B:公式推导
-
几何距离表示:
卫星 s s s 与接收机 r r r 之间的几何距离可以表示为它们位置向量的差:
ρ r s = ∣ r ⃗ s − r ⃗ r ∣ \rho_r^s = \left| \vec{r}^s - \vec{r}_r \right| ρrs=∣rs−rr∣
这里, r ⃗ s \vec{r}^s rs 是卫星的位置向量, r ⃗ r \vec{r}_r rr 是接收机的位置向量。 -
单点定位近似:
如果我们知道接收机的概略位置 r ⃗ 0 r \vec{r}_0^r r0r 和接收机位置的误差 d r ⃗ \vec{dr} dr,接收机的真实位置 r ⃗ r \vec{r}_r rr 可以表示为:
r ⃗ r = r ⃗ 0 r + d r ⃗ \vec{r}_r = \vec{r}_0^r + \vec{dr} rr=r0r+dr -
代入接收机的位置:
将接收机的真实位置代入几何距离公式:
ρ r s = ∣ r ⃗ s − ( r ⃗ 0 r + d r ⃗ ) ∣ \rho_r^s = \left| \vec{r}^s - (\vec{r}_0^r + \vec{dr}) \right| ρrs= rs−(r0r+dr) -
点积表示:
为了简化,我们通常用一个指向卫星的单位方向向量 u ⃗ r s \vec{u}_r^s urs 表示距离的点积:
ρ r s = ( r ⃗ s − ( r ⃗ 0 r + d r ⃗ ) ) ⋅ u ⃗ r s \rho_r^s = (\vec{r}^s - (\vec{r}_0^r + \vec{dr})) \cdot \vec{u}_r^s ρrs=(rs−(r0r+dr))⋅urs
这里, u ⃗ r s \vec{u}_r^s urs 是从接收机指向卫星的单位方向向量。 -
近似距离和误差项:
使用接收机的概略位置 r ⃗ 0 r \vec{r}_0^r r0r 计算的近似距离可以定义为:
R 0 s = ( r ⃗ s − r ⃗ 0 r ) ⋅ u ⃗ r s R_0^s = (\vec{r}^s - \vec{r}_0^r) \cdot \vec{u}_r^s R0s=(rs−r0r)⋅urs -
简化表达式:
将近似距离代入原始公式并简化:
ρ r s = ( r ⃗ s − ( r ⃗ 0 r + d r ⃗ ) ) ⋅ u ⃗ r s \rho_r^s = (\vec{r}^s - (\vec{r}_0^r + \vec{dr})) \cdot \vec{u}_r^s ρrs=(rs−(r0r+dr))⋅urs
ρ r s = ( r ⃗ s − r ⃗ 0 r − d r ⃗ ) ⋅ u ⃗ r s \rho_r^s = (\vec{r}^s - \vec{r}_0^r - \vec{dr}) \cdot \vec{u}_r^s ρrs=(rs−r0r−dr)⋅urs
ρ r s = ( r ⃗ s − r ⃗ 0 r ) ⋅ u ⃗ r s − d r ⃗ ⋅ u ⃗ r s \rho_r^s = (\vec{r}^s - \vec{r}_0^r) \cdot \vec{u}_r^s - \vec{dr} \cdot \vec{u}_r^s ρrs=(rs−r0r)⋅urs−dr⋅urs
ρ r s = R 0 s − d r ⃗ ⋅ u ⃗ r s \rho_r^s = R_0^s - \vec{dr} \cdot \vec{u}_r^s ρrs=R0s−dr⋅urs
最终公式
最终的公式是:
-
近似距离:
R 0 s = ( r ⃗ s − r ⃗ 0 r ) ⋅ u ⃗ r s R_0^s = (\vec{r}^s - \vec{r}_0^r) \cdot \vec{u}_r^s R0s=(rs−r0r)⋅urs -
考虑误差修正的真实几何距离:
ρ r s = ( r ⃗ s − ( r ⃗ 0 r + d r ⃗ ) ) ⋅ u ⃗ r s = R 0 s − d r ⃗ ⋅ u ⃗ r s \rho_r^s = (\vec{r}^s - (\vec{r}_0^r + \vec{dr})) \cdot \vec{u}_r^s = R_0^s - \vec{dr} \cdot \vec{u}_r^s ρrs=(rs−(r0r+dr))⋅urs=R0s−dr⋅urs
13.2.2 站间单差几何距离公式
13.1节中,我们已经通过站间单差基本消除了电离层误差和对流层误差,以及完全消除了卫星伪距硬件延迟和卫星钟差的影响。
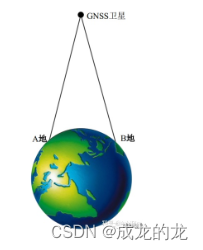
如果我们假设1号接收机为流动站,即我们仅能通过单点定位计算其粗略位置,而2号接收机为基准站,其精确的坐标已知。
ρ r 1 − 2 s = ρ r 1 s − ρ r 2 s \rho_{r1-2}^s = \rho_{r1}^s - \rho_{r2}^s ρr1−2s=ρr1s−ρr2s
- ρ r 1 − 2 s \rho_{r1-2}^s ρr1−2s 表示卫星 s s s 到测站1和测站2之间的几何距离差
- ρ r 1 s \rho_{r1}^s ρr1s 表示卫星 s s s 到测站1的几何距离
- ρ r 2 s \rho_{r2}^s ρr2s 表示卫星 s s s 到测站2的几何距离
但是我们知道广播星历实际上有误差的,如果我们假设其误差是 d r ⃗ s \vec{dr}^s drs。
- d r ⃗ s \vec{dr}^s drs 表示卫星 s s s 的位置误差向量
所以我们重写两个测站的几何距离公式:
流动站:
[ 概略位置 + 流动站位置偏差单位向量 + 卫星位置偏差单位向量]
ρ r 1 s = ( r ⃗ s + d r ⃗ s − ( r r 1 ⃗ + d r r 1 ⃗ ) ) ⋅ u ⃗ r 1 s = R 01 s − d r r 1 ⃗ ⋅ u ⃗ r 1 s + d r ⃗ s ⋅ u ⃗ r 1 s \rho_{r1}^s = (\vec{r}^s + \vec{dr}^s - (\vec{r_{r1}} + \vec{dr_{r1}})) \cdot \vec{u}_{r1}^s = R_{01}^s - \vec{dr_{r1}} \cdot \vec{u}_{r1}^s + \vec{dr}^s \cdot \vec{u}_{r1}^s ρr1s=(rs+drs−(rr1+drr1))⋅ur1s=R01s−drr1⋅ur1s+drs⋅ur1s
- r ⃗ s \vec{r}^s rs 表示卫星 s s s 的实际位置向量
- r r 1 ⃗ \vec{r_{r1}} rr1 表示测站1的实际位置向量
- d r r 1 ⃗ \vec{dr_{r1}} drr1 表示测站1的位置误差向量
- u ⃗ r 1 s \vec{u}_{r1}^s ur1s 表示从测站1到卫星 s s s 的单位方向向量
- R 01 s R_{01}^s R01s 表示由广播星历计算得到的卫星 s s s 到测站1的几何距离
基准站:
[ 概略位置 + 卫星位置偏差*单位向量]
ρ r 2 s = ( r ⃗ s + d r ⃗ s − ( r r 2 ⃗ ) ) ⋅ u ⃗ r 2 s = R 02 s + d r ⃗ s ⋅ u ⃗ r 2 s \rho_{r2}^s = (\vec{r}^s + \vec{dr}^s - (\vec{r_{r2}})) \cdot \vec{u}_{r2}^s = R_{02}^s + \vec{dr}^s \cdot \vec{u}_{r2}^s ρr2s=(rs+drs−(rr2))⋅ur2s=R02s+drs⋅ur2s
- r r 2 ⃗ \vec{r_{r2}} rr2 表示测站2的实际位置向量
- u ⃗ r 2 s \vec{u}_{r2}^s ur2s 表示从测站2到卫星 s s s 的单位方向向量
- R 02 s R_{02}^s R02s 表示由广播星历计算得到的卫星 s s s 到测站2的几何距离
上述中
R 01 s R_{01}^s R01s 代表卫星 s s s 广播星历位置到接收机1的概略位置的几何距离, R 02 s R_{02}^s R02s 代表卫星 s s s 广播星历位置到接收机2的真实几何距离,其他符号相似。
那么有
ρ r 1 − 2 s = ρ r 1 s − ρ r 2 s = ( R 01 s − d r r 1 ⃗ ⋅ u ⃗ r 1 s + d r ⃗ s ⋅ u ⃗ r 1 s ) − ( R 02 s + d r ⃗ s ⋅ u ⃗ r 2 s ) \rho_{r1-2}^s = \rho_{r1}^s - \rho_{r2}^s = (R_{01}^s - \vec{dr_{r1}} \cdot \vec{u}_{r1}^s + \vec{dr}^s \cdot \vec{u}_{r1}^s) - (R_{02}^s + \vec{dr}^s \cdot \vec{u}_{r2}^s) ρr1−2s=ρr1s−ρr2s=(R01s−drr1⋅ur1s+drs⋅ur1s)−(R02s+drs⋅ur2s)
那么有
ρ r 1 − 2 s = ( R 01 s − R 02 s ) − d r r 1 ⃗ ⋅ u ⃗ r 1 s + δ ρ s \rho_{r1-2}^s = (R_{01}^s - R_{02}^s) - \vec{dr_{r1}} \cdot \vec{u}_{r1}^s + \delta \rho^s ρr1−2s=(R01s−R02s)−drr1⋅ur1s+δρs
[(流动站概略位置到广播星历的距离 - 基准站位置到广播星历的距离)- 流动站接收机位置误差*单位向量+轨道误差在视线方向上投影的差值]
- δ ρ s \delta \rho^s δρs 为轨道误差在视线方向投影的差值
令 δ ρ s \delta \rho^s δρs 为轨道误差在视线方向投影的差值
δ ρ s = d r ⃗ s ⋅ u ⃗ r 1 s − d r ⃗ s ⋅ u ⃗ r 2 s = d r ⃗ s ⋅ ( u ⃗ r 1 s − u ⃗ r 2 s ) \delta \rho^s = \vec{dr}^s \cdot \vec{u}_{r1}^s - \vec{dr}^s \cdot \vec{u}_{r2}^s = \vec{dr}^s \cdot (\vec{u}_{r1}^s - \vec{u}_{r2}^s) δρs=drs⋅ur1s−drs⋅ur2s=drs⋅(ur1s−ur2s)
[ 轨道误差*两个视线单位向量的差 ] 都是极小量,轨道误差可以忽略。下面给出实际计算证明:
所以上述中我们主要考虑是 s s s 的轨道误差在两个测站观测方向上的投影差。
如果两个测站的方向余弦向量相差足够小,那么轨道误差通过星间单差后就可以忽略。
我们来简单假设一下,如果轨道误差在视线投影误差为20米,当测站相距20km时,那站间单差后的残余误差为 20 20000 × 20 = 1 20000 \frac{20}{20000} \times 20 = \frac{1}{20000} 2000020×20=200001米。
所以通过站间单差后,轨道的误差我们也可以忽略。
13.3 差分定位流程

相关文章:

让GNSSRTK不再难【第二天-第4部分】
第12讲 GNSS授时与PPS 12.1 为什么需要高精度时间 授时的传统理解就是时间传递或者对时。比如以前手机没这么方便时,大家还都使用石英钟手表看时间时,大家都习惯晚上七点准时对着中央一套的报时,来校准你家的机械钟或者挂钟,这就…...
「OC」UI练习(一)—— 登陆界面
「OC」登陆界面 明确要求 一个登陆界面的组成,用户名提示以及输入框,密码提示提示以及输入框,登陆按钮,以及注册按钮,根据以上要求我们将我们的组件设置为成员变量。 //viewControl.h #import <UIKit/UIKit.h>…...
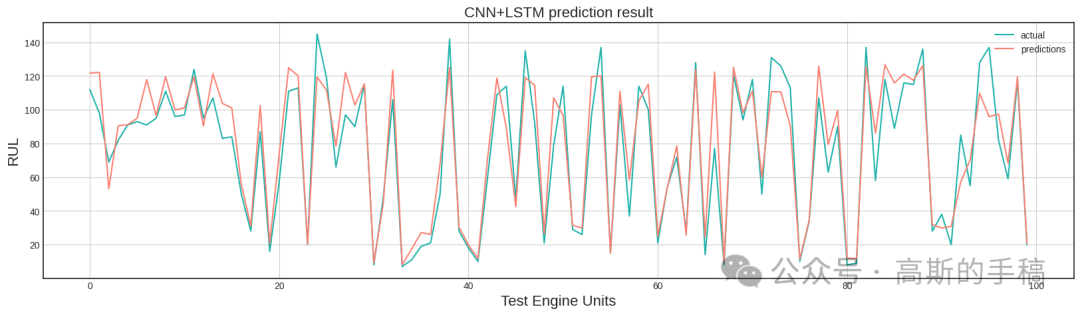
基于机器学习和深度学习的NASA涡扇发动机剩余使用寿命预测(C-MAPSS数据集,Python代码,ipynb 文件)
以美国航空航天局提供的航空涡扇发动机退化数据集为研究对象,该数据集包含多台发动机从启动到失效期间多个运行周期的多源传感器时序状态监测数据,它们共同表征了发动机的性能退化情况。为减小计算成本,需要对原始多源传感器监测数据进行数据…...
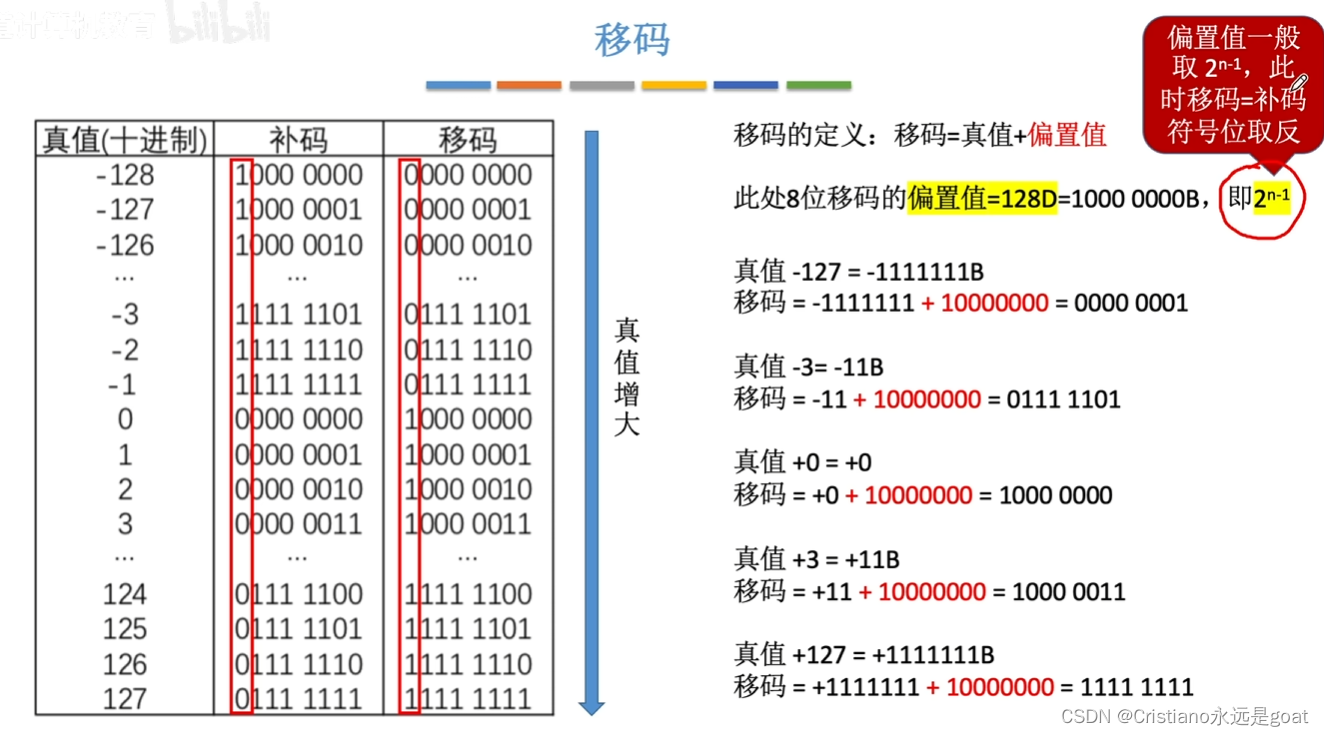
计算机组成原理-常见计算题含IEE754
一、补码加减运算 二、溢出判断 采用一位符号位 采用双符号位 三、定点数的移位运算 算术右移 算数左移 反码的算术移位 补码的算术移位 四、浮点数的表示 一个右规的例子 五、IEEE754 移码...

InnoDB存储引擎非常重要的一个机制--MVCC(多版本并发控制)
Mysql是如何实现隔离性的?(锁MVCC) 隔离性是指一个事务内部的操作以及操作的数据对正在进行的其他事务是隔离的,并发执行的各个事务之间不能相互干扰。隔离性可以防止多个事务并发执行时,可能存在交叉执行导致数据的不…...

【DevOps】服务器硬件基础知识
目录 前言 1、处理器(CPU):服务器的“大脑” 2、内存(RAM):服务器的“工作台” 3、存储(Storage):服务器的“仓库” 4、 网络接口(NIC)&…...

6.10 c语言
7.1 if-else语句 简化形式 if(表达式)语句块 阶梯形式 if(表达式1)语句块1 else if(表达式2)语句块2 嵌套形式 if() if() 语句1 else 语句2 else if() 语句3 else 语句4 表达式一般情况下为逻辑表达式或关系表达式 #include <stdio.h>//从小到大排序,输出顺…...

jenkins插件之Jdepend
JDepend插件是一个为构建生成JDepend报告的插件。 安装插件 JDepend Dashboard -->> 系统管理 -->> 插件管理 -->> Available plugins 搜索 Jdepend, 点击安装构建步骤新增执行shell #执行pdepend if docker exec phpfpm82 /tmp/composer/vendor/bin/pdepe…...

vue3之基于el-image实现图片预览
实现的功能: 图片可放大预览,支持放大、缩小、向左向右旋转查看可点击任意一张图后进行左右切换查看大图 主要使用的方法:splice和concat 主要代码 // template中 <div><el-imagev-for"(item, index) in imgsData":src&q…...
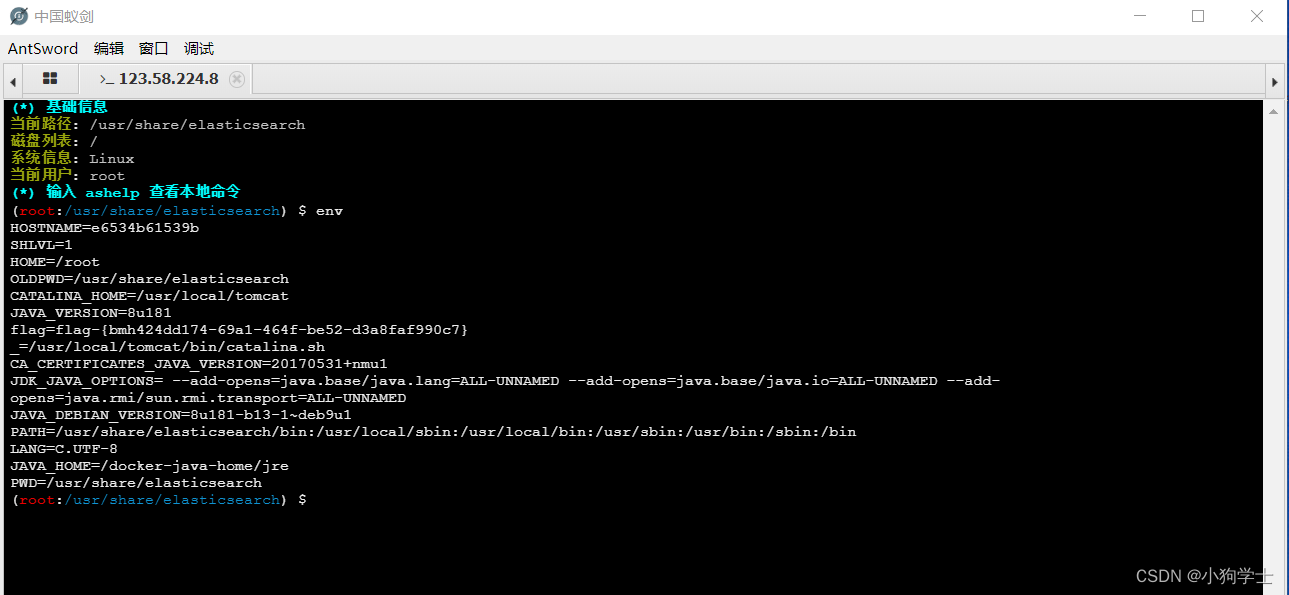
wooyun_2015_110216-Elasticsearch-vulfocus
1.原理 ElasticSearch具有备份数据的功能,用户可以传入一个路径,让其将数据备份到该路径下,且文件名和后缀都可控。 所以,如果同文件系统下还跑着其他服务,如Tomcat、PHP等,我们可以利用ElasticSearch的备…...
Fedora的远程桌面
要在 Fedora 40 上开启远程桌面功能。 首先,要确保已安装 gnome-remote-desktop 和 vino 包。 这些软件包通常默认安装在 Fedora 的 GNOME 桌面环境中。 可以按照以下步骤操作: 1、判断电脑是否安装了 gnome-remote-desktop 和 vino 包: tomfedora:…...
CSS id选择器
目录 任务描述 相关知识 id选择器 id选择器语法 类选择器与id选择器的区别 编程要求 任务描述 在本关中,你将通过id选择器的方式完成页面菜单栏样式布局,栏目导航等任务。 完成任务之后,基本页面效果如下: 动态效果如下&am…...
22.搭积木
上海市计算机学会竞赛平台 | YACSYACS 是由上海市计算机学会于2019年发起的活动,旨在激发青少年对学习人工智能与算法设计的热情与兴趣,提升青少年科学素养,引导青少年投身创新发现和科研实践活动。https://www.iai.sh.cn/problem/717 题目描述 小爱用积木搭起一座金字塔。为…...
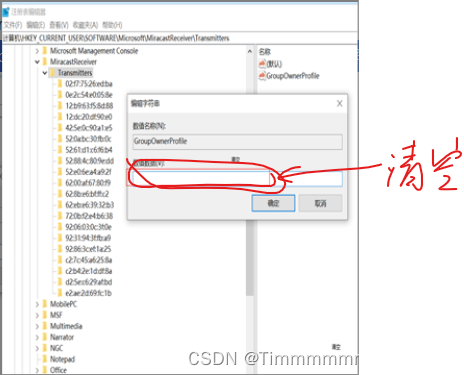
手机投屏到电脑时,手机提示连接失败
前言 注意,本方法建立在你已经通过其他帖子等解决了前置条件的情况下,手机提示连接失败情况下,包括但不限于关闭防火墙、安装无线投屏工具、手机和电脑连接在同一个WiFi频段下、关闭杀毒软件等。 具体操作方法 1、请进入设置 > 系统和…...

软件测试--Mysql快速入门
文章目录 软件测试-mysql快速入门sql主要划分mysql常用的数据类型sql基本操作常用字段的约束:连接查询mysql内置函数存储过程视图事务索引 软件测试-mysql快速入门 sql主要划分 sql语言主要分为: DQL:数据查询语言,用于对数据进…...

什么是PV操作
PV操作是一种在操作系统中用于同步和互斥的机制,它基于信号量(Semaphore)的概念。在并发编程中,多个进程或线程可能会同时访问共享资源,PV操作可以用来确保这些访问是同步的,以防止竞态条件和数据不一致的问题。 PV操作包括两个原子操作: P操作(Proberen,测试):这…...

差动放大器
差动器的出现是为了解决直接耦合电路存在的零点漂移问题,另外,差动放大器还有灵活的输入,输出方式。 一,基本差动放大器 差动放大器在电路结构上具有对称性,三极管VT1,VT2同型号,R1R2,R3R4,R5…...

【数据结构与算法 经典例题】括号匹配问题
💓 博客主页:倔强的石头的CSDN主页 📝Gitee主页:倔强的石头的gitee主页 ⏩ 文章专栏:《数据结构与算法 经典例题》C语言 期待您的关注 目录 一、问题描述 二、解题思路 🍃破解之道 🍃…...
2024年6月最新开源电视影视TVAPP原生源码和后台管理平台源码及完整教程
本套源码为本人维护更新完善半年左右的还在使用开发的源码,与市面上倒卖的残次品不一样,没有可比性,向下兼容安卓4.0,向上兼容安卓13以上TV电视系统, 完全无闪退,弹窗报错,卡死、异常死循环残次…...

[大模型]GLM4-9B-chat Lora 微调
本节我们简要介绍如何基于 transformers、peft 等框架,对 LLaMA3-8B-Instruct 模型进行 Lora 微调。Lora 是一种高效微调方法,深入了解其原理可参见博客:知乎|深入浅出 Lora。 这个教程会在同目录下给大家提供一个 nodebook 文件,…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
