量子计算的奥秘与魅力:开启未来科技的钥匙(详解)
目录
一、量子计算的基本概念
二、量子计算的基本原理
1.量子叠加态与相位态
一、概念
二、量子叠加态
定义与原理
特性与影响
应用领域
三、量子相位态
定义与原理
特性与影响
应用领域
2.量子门操作
一、概念
二、量子门操作的基本概念
三、常见的量子门操作
单比特量子门
两比特量子门
四、量子门操作的原理
五、量子门操作在量子计算中的应用
六、总结
3.量子纠缠
一、概念
二、量子纠缠的概念与原理
定义
原理
三、量子纠缠的特性
非局域性
不可分割性
瞬时性
量子通信
量子计算
量子密钥分发
其他应用
五、总结
三、量子计算的应用领域
四、量子计算的挑战与前景
五、结语
一、量子计算的基本概念
量子计算是一种遵循量子力学规律进行信息处理的新型计算模式。它与经典计算的本质区别在于,量子计算使用量子比特(qubit)作为基本信息单元,而非经典计算中的二进制位(bit)。量子比特具有叠加态和纠缠态等特性,这些特性使得量子计算在某些问题上具有远超经典计算的能力。
在量子计算中,一个量子比特可以同时处于0和1的叠加状态,这种状态被称为叠加态。叠加态的特性使得量子比特能够同时表示多种可能性,从而在处理某些问题时实现并行计算,大大提高了计算效率。此外,量子比特之间还可以发生纠缠,即一个量子比特的状态变化可以瞬间影响另一个与之纠缠的量子比特,这种特性为量子计算提供了更强大的信息处理能力。
二、量子计算的基本原理
1.量子叠加态与相位态
一、概念
量子叠加态与相位态是量子力学中的核心概念,它们为我们理解微观世界的奇特现象提供了基础。量子叠加态描述的是粒子在量子尺度上同时处于多种可能状态的叠加,而量子相位态则涉及到量子比特的相位信息。本文将详细解析这两个概念,并探讨它们在量子计算中的应用。
二、量子叠加态
-
定义与原理
-
量子叠加态是量子力学中最基本的概念之一,它描述了一个粒子在量子尺度上同时处于多种可能状态的叠加。这种叠加态不是简单的概率叠加,而是基于量子力学的叠加原理。叠加原理表明,如果一个系统可能处于几种不同的状态,那么这些状态的线性组合也是该系统的一个可能状态。
具体来说,一个量子比特可以处于两种基本状态:|0〉和|1〉(这里使用狄拉克符号表示量子态)。然而,根据量子叠加原理,量子比特还可以处于这两种状态的叠加态,表示为|ψ〉=α|0〉+β|1〉,其中α和β是复数,且满足|α|2+|β|2=1。这个方程描述了量子比特处于|0〉和|1〉两种状态的叠加,其中α和β分别表示处于这两种状态的概率幅度。
-
特性与影响
-
量子叠加态具有一些独特的特性,这些特性使得量子计算在某些问题上具有远超经典计算的能力。首先,量子叠加态的存在使得量子比特能够同时表示多种可能性,从而实现并行计算。这意味着在量子计算机上,我们可以同时处理多个计算任务,大大提高了计算效率。
其次,量子叠加态的叠加原理还导致了量子态的不确定性。在量子系统中,我们无法准确地知道一个粒子处于哪个状态,只能给出它处于各个状态的概率。这种不确定性使得量子计算在某些情况下能够避免经典计算中的某些困难问题,如NP完全问题。
此外,量子叠加态还与量子纠缠密切相关。当两个或多个粒子处于纠缠态时,它们的状态将相互依赖,无论它们之间的距离有多远。这种纠缠态的存在使得量子计算能够实现更高效的通信和计算任务。
-
应用领域
-
量子叠加态在量子计算中具有广泛的应用前景。首先,在量子通信领域,利用量子叠加态可以实现信息的传输和处理。例如,在量子密钥分发中,利用量子叠加态的不可克隆性和不可区分性可以确保通信的安全性。
其次,在量子计算领域,量子叠加态是实现量子并行性和量子加速的基础。例如,在量子搜索算法中,利用量子叠加态可以同时搜索多个目标项,从而实现比经典搜索算法更快的搜索速度。
此外,量子叠加态还在量子模拟、量子优化等领域发挥着重要作用。例如,在量子模拟中,利用量子叠加态可以模拟复杂的物理系统;在量子优化中,利用量子叠加态可以求解NP完全问题等优化问题。
三、量子相位态
-
定义与原理
-
量子相位态是指量子比特的相位可以取任意值的状态。在量子力学中,相位是描述波函数周期性变化的一个重要参数。对于量子比特来说,其相位态可以表示为|ψ〉=α|0〉+e^(iθ)β|1〉,其中α和β为复数,θ为相位角。这个方程描述了量子比特处于|0〉和|1〉两种状态的叠加,并且这两种状态之间存在一个相位差θ。
相位态的存在使得量子比特能够表示更丰富的信息。通过调整相位角θ的值,我们可以改变量子比特的状态和性质。这种能力使得量子计算在某些情况下能够实现更复杂的计算任务和更高效的通信方式。
-
特性与影响
-
量子相位态具有一些独特的特性,这些特性对量子计算具有重要的影响。首先,量子相位态的任意性使得我们可以根据需要调整量子比特的状态和性质。这种灵活性使得量子计算能够实现更复杂的计算任务和更高效的通信方式。
其次,量子相位态的周期性使得量子比特具有干涉和叠加的特性。这种特性使得量子计算在某些情况下能够避免经典计算中的某些困难问题,如NP完全问题。此外,量子相位态的干涉和叠加特性还使得量子计算具有更高的并行性和加速能力。
-
应用领域
-
量子相位态在量子计算中具有重要的应用价值。首先,在量子通信领域,利用量子相位态可以实现更高效的通信协议和更安全的加密方式。例如,在量子密钥分发中,利用量子相位态的不可克隆性和不可区分性可以确保通信的安全性。
其次,在量子计算领域,量子相位态是实现量子并行性和量子加速的关键。通过调整量子比特的相位角θ的值,我们可以实现更复杂的计算任务和更高效的计算方式。
2.量子门操作
一、概念
量子门操作是量子计算中的基本操作单元,用于对量子比特(qubit)进行状态变换和信息处理。类似于经典计算中的逻辑门(如与门、或门、非门等),量子门操作是构建量子算法和实现量子计算功能的核心。本文将详细解析量子门操作的概念、原理、特性及其在量子计算中的应用。
二、量子门操作的基本概念
量子门操作是量子计算中的基本操作单元,用于改变量子比特的状态或执行特定的量子运算。在量子计算中,一个量子比特的状态可以表示为一个二维复向量,通常使用狄拉克符号(如|0〉和|1〉)来表示。量子门操作则是对这些量子比特状态进行变换的线性算子。
量子门操作具有以下基本特性:
- 线性性质:量子门操作是线性变换,即如果量子门U作用于两个量子比特的叠加态,其效应将是分别对每个分量应用该门的效应的叠加。
- 幺正性:所有量子门操作都是幺正变换,即它们是幺正矩阵。幺正变换保持内积不变,因此保证了量子态的归一化和总概率为1。
三、常见的量子门操作
-
单比特量子门
(1)Pauli-X(NOT)门:Pauli-X门(也称为NOT门或X门)对量子比特进行逻辑非操作。它将量子比特的状态从|0〉翻转到|1〉,从|1〉翻转到|0〉。其矩阵表示为:
[ X = \begin{pmatrix} 0 & 1 \ 1 & 0 \end{pmatrix} ]
(2)Pauli-Y门:Pauli-Y门对量子比特进行相位翻转操作。它将|0〉变为i|1〉,将|1〉变为-i|0〉。其矩阵表示为:
[ Y = \begin{pmatrix} 0 & -i \ i & 0 \end{pmatrix} ]
(3)Pauli-Z门:Pauli-Z门(也称为相位门或Z门)对量子比特的相位进行翻转。它将|0〉保持不变,将|1〉变为-|1〉。其矩阵表示为:
[ Z = \begin{pmatrix} 1 & 0 \ 0 & -1 \end{pmatrix} ]
(4)Hadamard门:Hadamard门将量子比特从|0〉或|1〉状态转换为等概率的叠加态。其矩阵表示为:
[ H = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \ 1 & -1 \end{pmatrix} ]
-
两比特量子门
(1)CNOT(控制非)门:CNOT门是一个两比特量子门,其操作依赖于一个控制比特的状态。当控制比特为|0〉时,目标比特保持不变;当控制比特为|1〉时,目标比特执行NOT操作。CNOT门在量子计算中具有重要地位,它可以用来创建纠缠态。
(2)SWAP门:SWAP门是一个两比特量子门,用于交换两个量子比特的状态。它可以通过三个CNOT门来实现。
四、量子门操作的原理
量子门操作的原理基于量子力学中的线性代数和幺正变换理论。量子门操作可以看作是对量子比特状态空间中的向量进行线性变换的矩阵操作。这些矩阵操作保持量子态的归一化和总概率为1,这是通过幺正变换的性质来保证的。
量子门操作的另一个重要原理是量子叠加原理。量子比特可以处于多个状态的叠加态,而量子门操作可以将这些叠加态中的不同分量进行变换和组合,从而实现复杂的量子计算任务。
五、量子门操作在量子计算中的应用
量子门操作在量子计算中具有广泛的应用,包括量子通信、量子搜索、量子模拟和量子密码学等领域。例如,在量子通信中,量子门操作可以用于加密和解密信息;在量子搜索中,量子门操作可以实现比经典搜索算法更快的搜索速度;在量子模拟中,量子门操作可以模拟复杂的物理系统;在量子密码学中,量子门操作的精确控制和纠缠特性为量子密码学提供了理论和实验基础。
六、总结
量子门操作是量子计算中的基本操作单元,用于对量子比特进行状态变换和信息处理。它基于量子力学中的线性代数和幺正变换理论,具有线性性质、幺正性和量子叠加原理等特性。
3.量子纠缠
一、概念
量子纠缠是量子力学中一个极其重要的概念,它揭示了微观世界中粒子之间的一种特殊关联。当两个或多个粒子在某些物理性质上存在不可分割的关联时,即使这些粒子在空间上被分隔得足够远,以至于它们之间的任何相互作用都变得不可能,这些粒子仍然保持着一种深层次的联系。这种联系就是量子纠缠。本文将详细解析量子纠缠的概念、原理、特性及其在各个领域的应用。
二、量子纠缠的概念与原理
-
定义
量子纠缠描述的是两个或多个粒子之间通过纠缠态相互关联的现象。在量子力学中,两个粒子之间的纠缠态表示它们的状态无法单独描述,只能作为一个整体来描述。即使这两个粒子在空间上被分隔得足够远,它们的状态仍然是相互依赖的。
-
原理
量子纠缠的原理基于量子力学中的叠加原理和测量原理。叠加原理表明,一个量子系统可以处于多个可能状态的叠加态。而测量原理则指出,当我们对一个量子系统进行测量时,该系统的状态会瞬间坍缩到一个确定的状态。对于纠缠粒子来说,它们的状态是相互依赖的,因此当其中一个粒子被测量时,另一个粒子的状态也会立即发生变化,这种变化是瞬间的、不受距离限制的。
三、量子纠缠的特性
-
非局域性
量子纠缠的一个显著特性是非局域性。即使纠缠粒子在空间上被分隔得足够远,它们之间的关联仍然保持不变。这种非局域性使得量子纠缠成为量子通信和量子计算中的重要资源。
-
不可分割性
量子纠缠的另一个特性是不可分割性。纠缠粒子之间的关联是一种整体性质,无法被单独描述。这意味着纠缠粒子之间的关联是固有的、无法被分割的。
-
瞬时性
量子纠缠的瞬时性指的是当其中一个纠缠粒子被测量时,另一个粒子的状态会立即发生变化,这种变化是瞬间的、不受距离限制的。这种瞬时性使得量子纠缠成为实现即时通信的关键技术之一。
四、量子纠缠的应用
-
量子通信
量子纠缠是实现量子通信的关键技术之一。通过利用纠缠粒子之间的特殊关联,可以实现信息的即时传输和加密通信。量子通信具有传输速度快、安全性高等优点,因此在互联网、金融等领域有着广泛的应用前景。
-
量子计算
量子纠缠也是实现量子计算的重要技术之一。量子计算机利用量子纠缠和量子叠加等特性,可以在相同的计算资源下实现比传统计算机更快的计算速度。量子计算在优化问题、量子模拟等领域具有广泛的应用前景。
-
量子密钥分发
量子纠缠还可以用于实现量子密钥分发(QKD)。在QKD中,纠缠粒子被用作密钥的载体,通过测量纠缠粒子的状态来生成密钥。由于量子纠缠的瞬时性和不可分割性,QKD可以保证密钥在传输过程中不会被窃取或篡改,从而保证了通信的安全性。
-
其他应用
除了上述应用外,量子纠缠还在量子隐形传态、量子测量等领域发挥着重要作用。量子隐形传态是一种通过纠缠粒子之间的特殊关联实现信息传输的技术,而量子测量则利用纠缠粒子的特性来提高测量的精度和灵敏度。
五、总结
量子纠缠是量子力学中一个独特而重要的概念,它揭示了微观世界中粒子之间的一种特殊关联。量子纠缠具有非局域性、不可分割性和瞬时性等特性,这些特性使得量子纠缠在量子通信、量子计算等领域具有广泛的应用前景。随着量子技术的不断发展,量子纠缠将在更多领域展现出其独特的魅力和价值。
三、量子计算的应用领域
-
密码破译与加密:量子计算具有破解传统加密算法的能力,因此对国家信息安全具有重要战略意义。同时,量子计算也可以提供更加安全的加密方式,如量子密钥分发(QKD),确保通信的绝对安全性。
-
材料设计与药物研发:量子计算可以模拟和优化分子结构和反应,从而加速新材料的设计和新药的研发过程。这对于制药、能源等领域具有深远的影响。
-
优化问题:量子计算可以解决许多优化问题,如旅行商问题、物流优化等。通过量子计算的并行处理能力,可以提高运输和资源利用效率,为各行各业带来实质性的效益。
四、量子计算的挑战与前景
尽管量子计算具有巨大的潜力,但目前仍面临许多挑战。首先,量子比特的稳定性和可控性仍是关键问题,需要不断提高量子比特的相干时间和操作精度。其次,量子计算的商业化应用仍处于初级阶段,需要更多的研发和实践来推动其发展。此外,量子计算的安全性和伦理问题也需要引起关注。
然而,随着科技的不断进步和全球范围内的合作加强,量子计算有望实现更大的突破和发展。未来,量子计算有望在更多领域发挥重要作用,推动科技的进步和社会的发展。
五、结语
综上所述,量子计算作为一种新型的计算模式,具有巨大的潜力和广阔的应用前景。通过深入了解其基本原理和应用领域,我们可以更好地把握量子计算的发展趋势和未来挑战,为推动量子计算的进一步发展做出贡献。
respect!
相关文章:
)
量子计算的奥秘与魅力:开启未来科技的钥匙(详解)
目录 一、量子计算的基本概念 二、量子计算的基本原理 1.量子叠加态与相位态 一、概念 二、量子叠加态 定义与原理 特性与影响 应用领域 三、量子相位态 定义与原理 特性与影响 应用领域 2.量子门操作 一、概念 二、量子门操作的基本概念 三、常见的量子门操作…...

redis 主从同步时,是同步主节点的缓存积压区的数据,还是同步主节点的aof文件
Redis 的主从同步(replication)是同步主节点的数据到从节点上,但它既不是直接同步 AOF 文件,也不是同步缓存积压区。 当一个 Redis 从节点启动并连接到主节点时,会发生以下步骤: 同步数据集:从…...
Unity年中大促618活动又来了3折模板特效角色动画插件工具FPS生存建造模板RPG和2D素材优惠码UNITY6182024限时20240611
独立游戏开发需要找各种美术资源和模板,可以在低价时看看,节省开发时间。 Unity年中大促618活动又来了3折模板特效角色动画插件工具FPS生存建造模板RPG和2D素材优惠码UNITY6182024限时202406111104 300 款Unity引擎适配资源 3 折特惠,结账时输…...
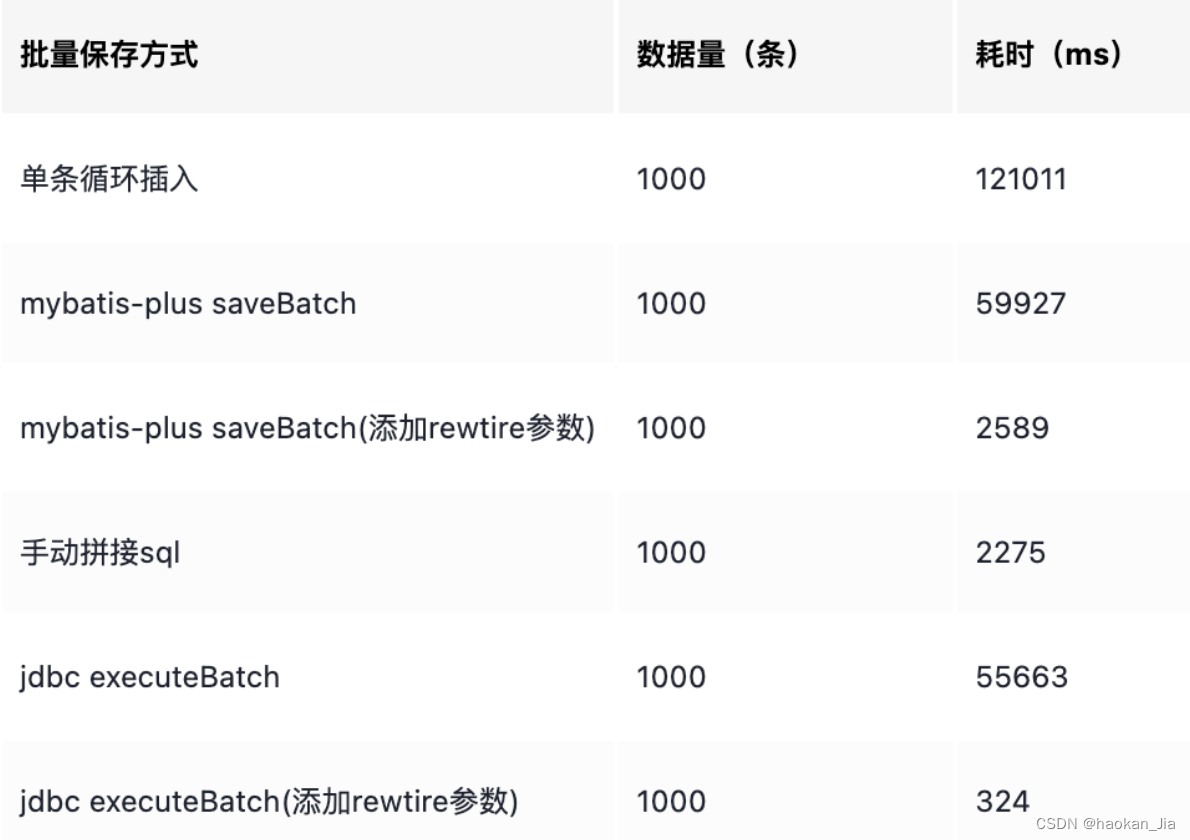
【MyBatis-plus】saveBatch 性能调优和【MyBatis】的数据批量入库
总结最优的两种方法: 方法1: 使用了【MyBatis-plus】saveBatch 但是数据入库效率依旧很慢,那可能是是因为JDBC没有配置,saveBatch 批量写入并没有生效哦!!! 详细配置如下:批量数据入…...

前端三剑客之JavaScript基础入门
目录 ▐ 快速认识JavaScript ▐ 基本语法 🔑JS脚本写在哪? 🔑注释 🔑变量如何声明? 🔑数据类型 🔑运算符 🔑流程控制 ▐ 函数 ▐ 事件 ▐ 计时 ▐ HTML_DOM对象 * 建议学习完HTML和CSS后再…...

Fyndiq买家号下单:自养号测评如何打造本土物理环境系统?
Fyndiq 是一个瑞典电子商务平台,我们通过该平台为渴望讨价还价的购物者提供一系列产品。该公司为希望以可访问的方式提高销售额的所有类型的零售商提供销售渠道。Fyndiq几乎是瑞典家喻户晓的存在,是瑞典折扣促销平台。以销售质优价廉的商品吸引了大量忠实…...
自动检测曲别针数量:图像处理技术的应用
引言 在这篇博客中,我们将探讨如何使用计算机视觉技术自动检测图像中曲别针的数量。 如图: [1]使用灰度转换 由于彩色信息对于曲别针计数并不重要,我们将图像转换为灰度图,这样可以减少处理数据的复杂度,加速后续的…...
【Git】多人协作 -- 详解
一、多人协作(1) ⽬前,我们所完成的工作如下: 基本完成 Git 的所有本地库的相关操作,git 基本操作,分支理解,版本回退,冲突解决等等。 申请码云账号,将远端信息 clone…...

Eureka和Nacos有哪些区别?
Eureka和Nacos都能起到注册中心的作用,用法基本类似。但还是有一些区别的,例如: Nacos支持配置管理,而Eureka则不支持。 而且服务注册发现上也有区别,我们来做一个实验: 我们停止user-service服务&#x…...

如何正确使用 include-what-you-use
简单地说,由 Google 开发的 include-what-you-use(IWYU)让源代码文件包含代码里用到的所有头文件。这种方法确保在改动了一些接口之后,代码依然最有可能编译成功。 之前我写了一篇关于 include-what-you-use 工具的文章ÿ…...

企业内网安全软件分享,有什么内网安全软件
内网安全? 其实就是网络安全的一种。 什么是内网安全软件? 内网安全软件是企业保障内网安全的一种重要工具。 它主要帮助企业实现对网络设备、应用程序、用户行为等方面的监控和管理,以预防和应对各种网络攻击。 这类软件主要用于对内网中…...

【摘葡萄game】
您想要了解的“摘葡萄游戏”可能是一个编程项目或者是一个编程相关的练习。我可以提供一个简单的摘葡萄游戏的思路和代码示例。这个游戏可以用多种编程语言来实现,比如Python、Java等。这里我以Python为例,给出一个基础版本的摘葡萄游戏的概念和代码。 …...

java如何实现字符串连接
在java中,字符串与字符串连接可以用运算符和 比如有字符串a,字符串b 想要把a和b连接起来,定义一个字符串变量c cab 或者 ab 示例代码 public class Zifuchuanlianjie {public static void main(String[] args) {String a"我叫李狗蛋";S…...

流量卡选卡攻略,拯救不会选流量卡的小白!
家人们,你们知道不,选择一款性价比高的流量卡,真的超级省钱。 一、首先,说一说申请。 运营商推出线上流量卡,注意是线上的流量卡,都是免费领取,运营商包邮到家,在激活充值之前不…...

python class __format__ __bytes__区别
在Python中,__format__和__bytes__是两个特殊方法,它们允许对象自定义它们在特定情境下的字符串表示。以下是这两个方法的区别和作用: __format__ 作用:__format__方法用于定义对象在使用format()函数或格式化字符串(…...

C++ | Leetcode C++题解之第134题加油站
题目: 题解: class Solution { public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int n gas.size();int i 0;while (i < n) {int sumOfGas 0, sumOfCost 0;int cnt 0;while (cnt < n) {int j (i …...
【Linux】ls命令
这个命令主要是用于显示指定工作目录下之内容(列出目前工作目录所含的文件及子目录)。 掌握几个重点的常使用的就可以: ls -l # 以长格式显示当前目录中的文件和目录 ls -a # 显示当前目录中的所有文件和目录&am…...

多态、虚函数表与动态绑定的深入解析
目录 多态简介 虚函数表与动态绑定 虚函数表 动态绑定机制 内存与性能影响 纯虚函数与抽象类 纯虚函数 抽象类 动态类型转换与typeid操作符 dynamic_cast typeid操作符 虚析构函数的重要性 在面向对象编程中,多态性是一种核心特性,它允许我们…...

VitePress+Docker+jenkins构建个人网站
VitePress官网 VitePress | 由 Vite 和 Vue 驱动的静态站点生成器 可以理解为一个前端脚手架:快速生成个人站点 最好先大概看一遍 快速开始 | VitePress 可以在线体验一下 安装条件 node -v 检查下node版本 在D盘创建一个文件夹 例如:VitePress 进入文件夹 cmd npm ini…...

Windows11下Docker使用记录(五)
目录 准备1. WSL安装cuda container toolkit2. win11 Docker Desktop 设置3. WSL创建docker container并连接cuda4. container安装miniconda(可选) Docker容器可以从底层虚拟化,使我们能够在 不降级 CUDA驱动程序的情况下使用 任何版本的CU…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
