Apollo9.0 PNC源码学习之Control模块(二)
前面文章:Apollo9.0 PNC源码学习之Control模块(一)
本文将对具体控制器以及原理做一个剖析

1 PID控制器
1.1 PID理论基础
如下图所示,PID各参数(Kp,Ki,Kd)的作用:


 任何闭环控制系统的首要任务是要稳、准、快的响应命令。PID的主要工作就是如何实现这一任务。
任何闭环控制系统的首要任务是要稳、准、快的响应命令。PID的主要工作就是如何实现这一任务。
PID控制器的比例单元 ( P) 、积分单元(I)和微分单元(D)分别对应目前误差、过去累计误差及未来误差。若是不知道受控系统的特性,一般认为PID控制器是最适用的控制器。
P:增大比例加快系统的响应,它的作用于输出值较快,但不能很好稳定在一个理想的数值。Kp过大,会产生超调,并产生振荡。
I:在P的基础上消除余差,对稳定后有累积误差的系统进行误差修整,减小稳态误差。
D:可以使系统超调量减小,减小振荡,增加稳定性。
位置式PID:当前系统的实际位置,与你想要达到的预期位置的偏差,进行PID控制
 当采样时间足够小时,能够获得最够精确的结果,离散控制过程与连续过程非常接近。
当采样时间足够小时,能够获得最够精确的结果,离散控制过程与连续过程非常接近。
位置式PID在积分项达到饱和时,误差仍然会在积分作用下继续累积,一旦误差开始反向变化,系统需要一定时间从饱和区退出,所以在u(k)达到最大和最小时,要停止积分作用,并且要有积分限幅和输出限幅。
抗积分饱和:如果上一次的输出控制量超过了饱和值,饱和值为正,则这一次只积分负的偏差,饱和值为负,则这一次只积分正的偏差,从而避免系统长期留在饱和区!
1.2 Apollo的经典PID源码
modules/control/control_component/proto/pid_conf.proto
syntax = "proto2";package apollo.control;message PidConf {optional bool integrator_enable = 1;optional double integrator_saturation_level = 2;optional double kp = 3;optional double ki = 4;optional double kd = 5;optional double kaw = 6 [default = 0.0];optional double output_saturation_level = 7;
}
pid_controller.h
#pragma once#include "modules/control/control_component/proto/pid_conf.pb.h"namespace apollo {
namespace control {class PIDController {public:// 初始化pid控制器void Init(const PidConf &pid_conf);// 设置pid参数void SetPID(const PidConf &pid_conf);// 重置pidvoid Reset();// 重置积分项void Reset_integral();// PID控制实现(误差+采样时间)virtual double Control(const double error, const double dt);// 默认虚析构函数virtual ~PIDController() = default;// 获取积分器(Integrator)的过饱和状态int IntegratorSaturationStatus() const;// 检查积分器(Integrator)是否处于保持状态bool IntegratorHold() const;// 设置积分器(Integrator)是否保持当前值void SetIntegratorHold(bool hold);protected:double kp_ = 0.0;double ki_ = 0.0;double kd_ = 0.0;double kaw_ = 0.0;double previous_error_ = 0.0;double previous_output_ = 0.0;double integral_ = 0.0;double integrator_saturation_high_ = 0.0;double integrator_saturation_low_ = 0.0;bool first_hit_ = false;bool integrator_enabled_ = false;bool integrator_hold_ = false;int integrator_saturation_status_ = 0;// Only used for pid_BC_controller and pid_IC_controllerdouble output_saturation_high_ = 0.0;double output_saturation_low_ = 0.0;int output_saturation_status_ = 0;
};} // namespace control
} // namespace apollo
pid_controller.cc
#include "modules/control/control_component/controller_task_base/common/pid_controller.h"#include <cmath>#include "cyber/common/log.h"namespace apollo {
namespace control {double PIDController::Control(const double error, const double dt) {// 如果dt小于等于0,使用上一次输出if (dt <= 0) {AWARN << "dt <= 0, will use the last output, dt: " << dt;return previous_output_;}double diff = 0; // 差值double output = 0;// 输出// 如果是第一次运行if (first_hit_) {first_hit_ = false;} else {// 计算差值diff = (error - previous_error_) / dt;}// 积分 如果不启用积分,积分置为零if (!integrator_enabled_) {integral_ = 0;} else if (!integrator_hold_) {// 计算积分integral_ += error * dt * ki_;// 在积分之前应用Ki,以避免在稳态时改变Ki时的阶梯效应if (integral_ > integrator_saturation_high_) {// 如果积分大于饱和上限,将积分设置为饱和上限integral_ = integrator_saturation_high_;// 设置饱和状态为1integrator_saturation_status_ = 1;} else if (integral_ < integrator_saturation_low_) {// 如果积分小于饱和下限,将积分设置为饱和下限integral_ = integrator_saturation_low_;// 设置饱和状态为-1integrator_saturation_status_ = -1;} else {// 如果积分在饱和范围内,设置饱和状态为0integrator_saturation_status_ = 0;}}// 更新previous_error_previous_error_ = error;// 计算输出output = error * kp_ + integral_ + diff * kd_; // Ki already applied// 更新previous_output_previous_output_ = output;return output;
}
// 重置积分项
void PIDController::Reset_integral() {integral_ = 0.0;integrator_saturation_status_ = 0;
}
// 重置PID控制器
void PIDController::Reset() {previous_error_ = 0.0;previous_output_ = 0.0;integral_ = 0.0;first_hit_ = true;integrator_saturation_status_ = 0;output_saturation_status_ = 0;
}
// 初始化控制器
void PIDController::Init(const PidConf &pid_conf) {previous_error_ = 0.0;previous_output_ = 0.0;integral_ = 0.0;first_hit_ = true;integrator_enabled_ = pid_conf.integrator_enable();integrator_saturation_high_ =std::fabs(pid_conf.integrator_saturation_level());integrator_saturation_low_ =-std::fabs(pid_conf.integrator_saturation_level());integrator_saturation_status_ = 0;integrator_hold_ = false;output_saturation_high_ = std::fabs(pid_conf.output_saturation_level());output_saturation_low_ = -std::fabs(pid_conf.output_saturation_level());output_saturation_status_ = 0;SetPID(pid_conf);
}
// 设置PID参数
void PIDController::SetPID(const PidConf &pid_conf) {kp_ = pid_conf.kp();ki_ = pid_conf.ki();kd_ = pid_conf.kd();kaw_ = pid_conf.kaw();
}
// 积分饱和状态
int PIDController::IntegratorSaturationStatus() const {return integrator_saturation_status_;
}
// 是否积分保持
bool PIDController::IntegratorHold() const { return integrator_hold_; }
// 设置积分保持(true or false)
void PIDController::SetIntegratorHold(bool hold) { integrator_hold_ = hold; }} // namespace control
} // namespace apollo
以上对经典PID的源码进行了剖析,额外对百度Apollo采用其他PID算法进行源码讲解
1.3 pid_IC_controller
pid_IC_controller.h
#pragma once#include "modules/control/control_component/proto/pid_conf.pb.h"#include "modules/control/control_component/controller_task_base/common/pid_controller.h"namespace apollo {
namespace control {
// 该类继承于PIDController
class PIDICController : public PIDController {public:// PIDICController控制virtual double Control(const double error, const double dt);// 输出饱和状态virtual int OutputSaturationStatus();private:
};} // namespace control
} // namespace apollo
pid_IC_controller.cc
#include "modules/control/control_component/controller_task_base/common/pid_IC_controller.h"#include <cmath>
#include <iostream>#include "cyber/common/log.h"
#include "modules/common/math/math_utils.h"namespace apollo {
namespace control {double PIDICController::Control(const double error, const double dt) {// 如果dt小于等于0,使用上一次输出if (dt <= 0) {AWARN << "dt <= 0, will use the last output";return previous_output_;}double diff = 0; // 差值double output = 0;// 输出// 如果是第一次运行if (first_hit_) {first_hit_ = false;} else {diff = (error - previous_error_) / dt;}// integral clamping// 积分限幅if (!integrator_enabled_) {integral_ = 0;} else {double u = error * kp_ + integral_ + error * dt * ki_ + diff * kd_;// 如果error和u同一方向 输出u在饱和范围外,不更新积分项if (((error * u) > 0) &&((u > output_saturation_high_) || (u < output_saturation_low_))) {} else {// Only update integral then// 仅仅更新积分integral_ += error * dt * ki_;}}// 更新previous_error_previous_error_ = error;output = error * kp_ + integral_ + diff * kd_;if (output >= output_saturation_high_) {output_saturation_status_ = 1;} else if (output <= output_saturation_low_) {output_saturation_status_ = -1;} else {output_saturation_status_ = 0;}// 限制output在输出饱和范围内output = common::math::Clamp(error * kp_ + integral_ + diff * kd_,output_saturation_high_,output_saturation_low_); // Ki already appliedprevious_output_ = output;return output;
}
// 返回输出饱和状态
int PIDICController::OutputSaturationStatus() {return output_saturation_status_;
}} // namespace control
} // namespace apollo
1.4 pid_BC_controller
反向计算pid
pid_BC_controller.h
#pragma once#include "modules/control/control_component/proto/pid_conf.pb.h"#include "modules/control/control_component/controller_task_base/common/pid_controller.h"namespace apollo {
namespace control {class PIDBCController : public PIDController {public:virtual double Control(const double error, const double dt);virtual int OutputSaturationStatus();private:
};} // namespace control
} // namespace apollo
pid_BC_controller.cc
#include "modules/control/control_component/controller_task_base/common/pid_BC_controller.h"#include <cmath>#include "cyber/common/log.h"
#include "modules/common/math/math_utils.h"namespace apollo {
namespace control {
// PIDBCController控制
double PIDBCController::Control(const double error, const double dt) {// 如果dt小于等于0,使用上一次输出if (dt <= 0) {AWARN << "dt <= 0, will use the last output";return previous_output_;}double diff = 0;double output = 0;if (first_hit_) {first_hit_ = false;} else {diff = (error - previous_error_) / dt;}// backward calculation 反向计算if (!integrator_enabled_) { // 如果积分器未启用,则将积分设置为0integral_ = 0;} else {double u = error * kp_ + integral_ + error * dt * ki_ + diff * kd_;// 本人认为aw_term是计算超出u的值,然后根据aw_term判断输出饱和状态double aw_term = common::math::Clamp(u, output_saturation_high_,output_saturation_low_) -u;if (aw_term > 1e-6) {output_saturation_status_ = -1;} else if (aw_term < -1e-6) {output_saturation_status_ = 1;} else {output_saturation_status_ = 0;}// 计算积分integral_ += kaw_ * aw_term + error * dt;}// 更新previous_error_previous_error_ = error;// 限制输出在输出饱和状态内output = common::math::Clamp(error * kp_ + integral_ + diff * kd_,output_saturation_high_,output_saturation_low_); // Ki already appliedprevious_output_ = output;return output;
}
// 返回输出饱和状态
int PIDBCController::OutputSaturationStatus() {return output_saturation_status_;
}} // namespace control
} // namespace apollo
2 超前滞后控制器leadlag_controller
主要用于倒车运动控制
2.1 超前滞后控制器源码解析
leadlag_controller.h
#pragma once#include "modules/control/control_component/proto/leadlag_conf.pb.h"namespace apollo {
namespace control {class LeadlagController {public:// 初始化void Init(const LeadlagConf &leadlag_conf, const double dt);// 设置leadlag alpha, beta and tauvoid SetLeadlag(const LeadlagConf &leadlag_conf);// 双线性变换离散化方法(T型积分:曲线包围面积用梯形估算)// 把连续的控制器系数离散化void TransformC2d(const double dt);// 重置超前滞后控制器void Reset();// 超前滞后也是类似PID输入参数error和dtvirtual double Control(const double error, const double dt);// 获取饱和状态int InnerstateSaturationStatus() const;protected:// 连续时间控制系数double alpha_ = 0.0;double beta_ = 0.0;double tau_ = 0.0;double Ts_ = 0.01; // 默认0.01s// 离散时间控制系数double kn1_ = 0.0;double kn0_ = 0.0;double kd1_ = 0.0;double kd0_ = 0.0;// Inner (intermedia) state in discrete-time domain at Direct Form IIdouble previous_output_ = 0.0;double previous_innerstate_ = 0.0;double innerstate_ = 0.0;double innerstate_saturation_high_ = 0.0;double innerstate_saturation_low_ = 0.0;int innerstate_saturation_status_ = 0;// 是否启用从连续时间到离散时间的转换bool transfromc2d_enabled_ = false;
};} // namespace control
} // namespace apollo
leadlag_controller.cc
#include "modules/control/control_component/controller_task_base/common/leadlag_controller.h"#include <cmath>#include "cyber/common/log.h"namespace apollo {
namespace control {double LeadlagController::Control(const double error, const double dt) {// check if the c2d transform passed during the initilization// 判断连续转离散是否成功if (!transfromc2d_enabled_) {// 失败则重新进行TransformC2dTransformC2d(dt);if (!transfromc2d_enabled_) { // 再次失败,则发出警告AWARN << "C2d transform failed; will work as a unity compensator, dt: "<< dt;return error; // treat the Lead/Lag as a unity proportional controller}}// check if the current sampling time is valid// 检查步长dt是否小于等于零if (dt <= 0.0) {AWARN << "dt <= 0, will use the last output, dt: " << dt;return previous_output_;}double output = 0.0;// 计算内部状态innerstate_innerstate_ = (error - previous_innerstate_ * kd0_) / kd1_; // calculate// the inner (intermedia) state under the Direct form II for the Lead / Lag// compensator factorization// 进行innerstate幅值判断:高于状态饱和上限,则等于状态饱和上限,并将状态饱和状态置1;// 低于状态饱和下限,则等于状态饱和下限,并将状态饱和状态置-1;其余情况状态饱和状态置0if (innerstate_ > innerstate_saturation_high_) {innerstate_ = innerstate_saturation_high_;innerstate_saturation_status_ = 1;} else if (innerstate_ < innerstate_saturation_low_) {innerstate_ = innerstate_saturation_low_;innerstate_saturation_status_ = -1;} else {innerstate_saturation_status_ = 0;}// 计算输出output = innerstate_ * kn1_ + previous_innerstate_ * kn0_;// 更新previous_innerstate_previous_innerstate_ = innerstate_;// 更新previous_output_previous_output_ = output;return output;
}void LeadlagController::Reset() {previous_output_ = 0.0;previous_innerstate_ = 0.0;innerstate_ = 0.0;innerstate_saturation_status_ = 0;
}void LeadlagController::Init(const LeadlagConf &leadlag_conf, const double dt) {// 前一输出previous_output_ = 0.0;// 前一内部状态previous_innerstate_ = 0.0;// 内部状态innerstate_ = 0.0;// 内部状态饱和上限innerstate_saturation_high_ =std::fabs(leadlag_conf.innerstate_saturation_level());// 内部状态饱和下限innerstate_saturation_low_ =-std::fabs(leadlag_conf.innerstate_saturation_level());// 内部状态饱和标志innerstate_saturation_status_ = 0;// 设置leadlagSetLeadlag(leadlag_conf);// 连续转离散 TransformC2d函数的作用是将连续形式的传递函数转换成离散形式的传递函数TransformC2d(dt);
}void LeadlagController::SetLeadlag(const LeadlagConf &leadlag_conf) {alpha_ = leadlag_conf.alpha();beta_ = leadlag_conf.beta();tau_ = leadlag_conf.tau();
}void LeadlagController::TransformC2d(const double dt) {if (dt <= 0.0) {AWARN << "dt <= 0, continuous-discrete transformation failed, dt: " << dt;transfromc2d_enabled_ = false;} else {double a1 = alpha_ * tau_;double a0 = 1.00;double b1 = beta_ * tau_;double b0 = beta_;Ts_ = dt;kn1_ = 2 * b1 + Ts_ * b0;kn0_ = Ts_ * b0 - 2 * b1;kd1_ = 2 * a1 + Ts_ * a0;kd0_ = Ts_ * a0 - 2 * a1;if (kd1_ <= 0.0) {AWARN << "kd1 <= 0, continuous-discrete transformation failed, kd1: "<< kd1_;transfromc2d_enabled_ = false;} else {transfromc2d_enabled_ = true;}}
}
// 返回内部饱和状态
int LeadlagController::InnerstateSaturationStatus() const {return innerstate_saturation_status_;
}} // namespace control
} // namespace apollo
2.2 超前滞后控制器原理讲解
leadlag传递函数:
H ( s ) = β τ s + 1 τ α s + 1 H(s)=\beta \frac{\tau s+1}{\tau \alpha s+1} H(s)=βταs+1τs+1
其中,
τ \tau τ:时间常数
α \alpha α:超前滞后调节系数
β \beta β:开环增益系数
( 1 − α ) τ (1-\alpha)\tau (1−α)τ:需要超前或滞后的时间
当 α < 1 \alpha<1 α<1,有 τ > α τ \tau>\alpha\tau τ>ατ:超前补偿
当 α > 1 \alpha>1 α>1,有 τ < α τ \tau<\alpha\tau τ<ατ:滞后补偿
采用双线性变换,T为采样周期
s = 2 T z − 1 z + 1 s=\frac{2}{T} \frac{z-1}{z+1} s=T2z+1z−1
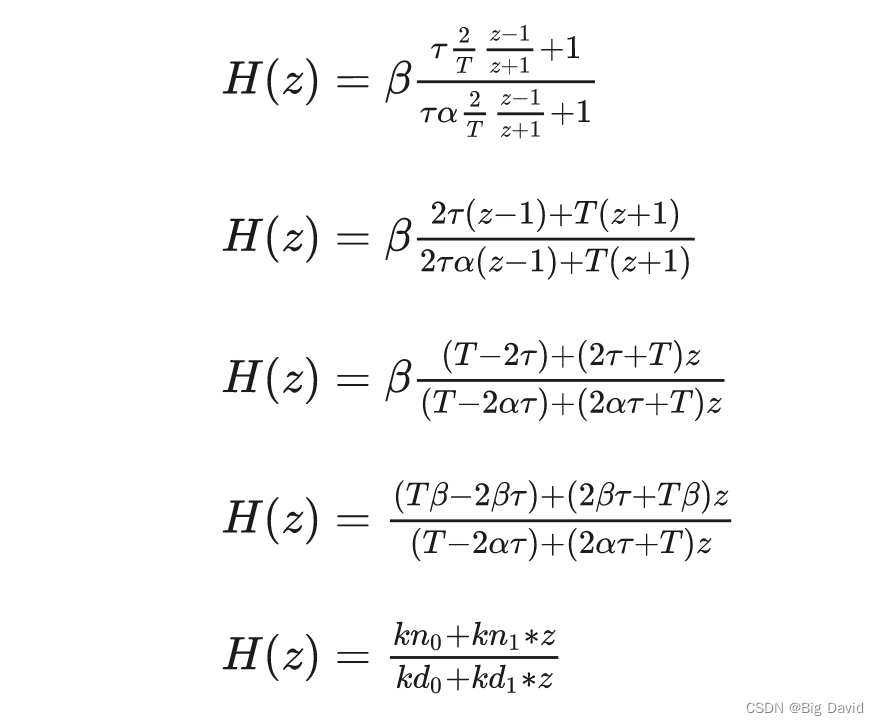 从上述公式来看,和代码里是一致的:
从上述公式来看,和代码里是一致的:
α 1 = α τ , α 0 = 1.00 , b 1 = β τ , b 0 = β \alpha1=\alpha\tau,\alpha0=1.00,b1=\beta\tau,b0=\beta α1=ατ,α0=1.00,b1=βτ,b0=β
k n 1 = 2 β τ + T β kn_1=2\beta\tau+T\beta kn1=2βτ+Tβ
k n 0 = T β − 2 β τ kn_0=T\beta-2\beta\tau kn0=Tβ−2βτ
k d 1 = 2 α τ + T kd_1=2\alpha\tau+T kd1=2ατ+T
k d 0 = T − 2 α τ kd_0=T-2\alpha\tau kd0=T−2ατ
double a1 = alpha_ * tau_;
double a0 = 1.00;
double b1 = beta_ * tau_;
double b0 = beta_;
Ts_ = dt;
kn1_ = 2 * b1 + Ts_ * b0;
kn0_ = Ts_ * b0 - 2 * b1;
kd1_ = 2 * a1 + Ts_ * a0;
kd0_ = Ts_ * a0 - 2 * a1;
if (kd1_ <= 0.0) {AWARN << "kd1 <= 0, continuous-discrete transformation failed, kd1: "<< kd1_;transfromc2d_enabled_ = false;
} else {transfromc2d_enabled_ = true;
}
相位角和幅值:
超前-滞后补偿器的传递函数相角为:
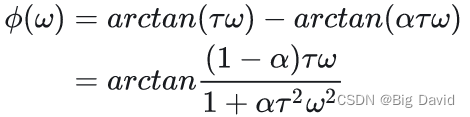 式中,计算公式参考和差化积
式中,计算公式参考和差化积
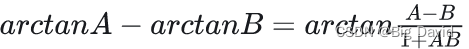 最大相角在极点 1 α τ \frac{1}{\alpha\tau} ατ1和零点 1 τ \frac{1}{\tau} τ1之间,其值取决于 α \alpha α的大小
最大相角在极点 1 α τ \frac{1}{\alpha\tau} ατ1和零点 1 τ \frac{1}{\tau} τ1之间,其值取决于 α \alpha α的大小


参数分析:
 在工程实践中,可以通过提高系统其他环节的放大系数或增加比例放大器加以补偿,Apollo的leadlag采用后者的处理方法。但是 β \beta β如果过大,容易引起饱和
在工程实践中,可以通过提高系统其他环节的放大系数或增加比例放大器加以补偿,Apollo的leadlag采用后者的处理方法。但是 β \beta β如果过大,容易引起饱和
innerstate_ = (error - previous_innerstate_ * kd0_) / kd1_;

3 Apollo的模型参考自适应控制MRAC
MRAC原理:一般用于百度Apollo横向控制
参考博客
MRAC控制系统的基本结构图
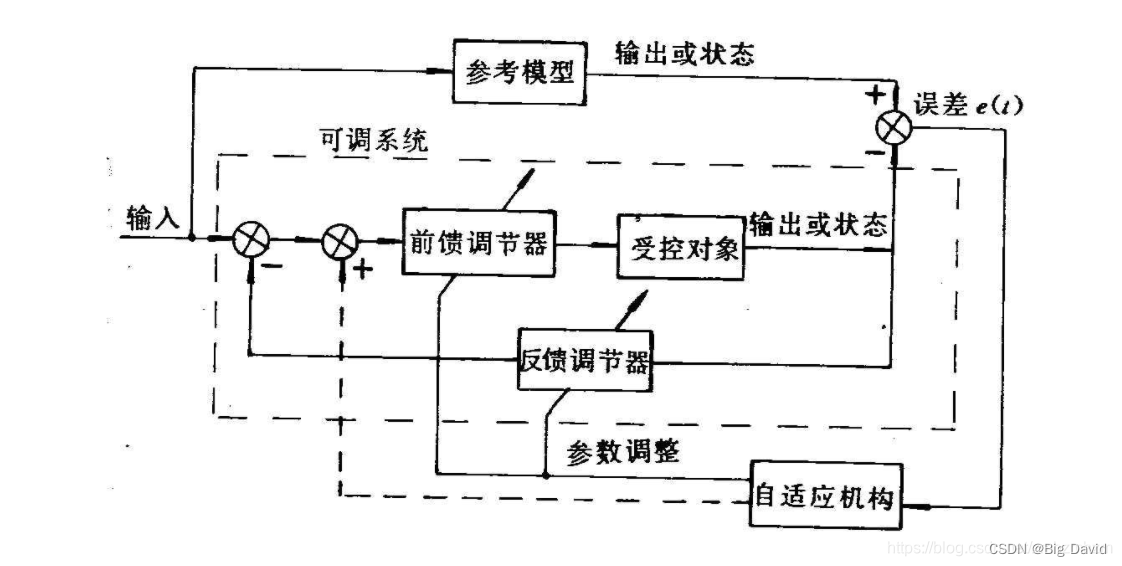 控制器和受控对象组成内环,这一部分称之为可调系统,由参考模型和自适应机构组成外环。
控制器和受控对象组成内环,这一部分称之为可调系统,由参考模型和自适应机构组成外环。
该系统是在常规的反馈控制回路上再附加一个参考模型和控制器参数的自动调节回路而形成。在该系统中,参考模型的输出或状态相当于给定一个动态性能指标,目标信号同时加在可调系统与参考模型上,通过比较受控对象与参考模型的输出或状态来得到两者之间的误差信息,按照一定的规律(自适应律)来修正控制器的参数(参数自适应)或产生一个辅助输入信号(信号综合自适应),从而使受控制对象的输出尽可能地跟随参考模型的输出
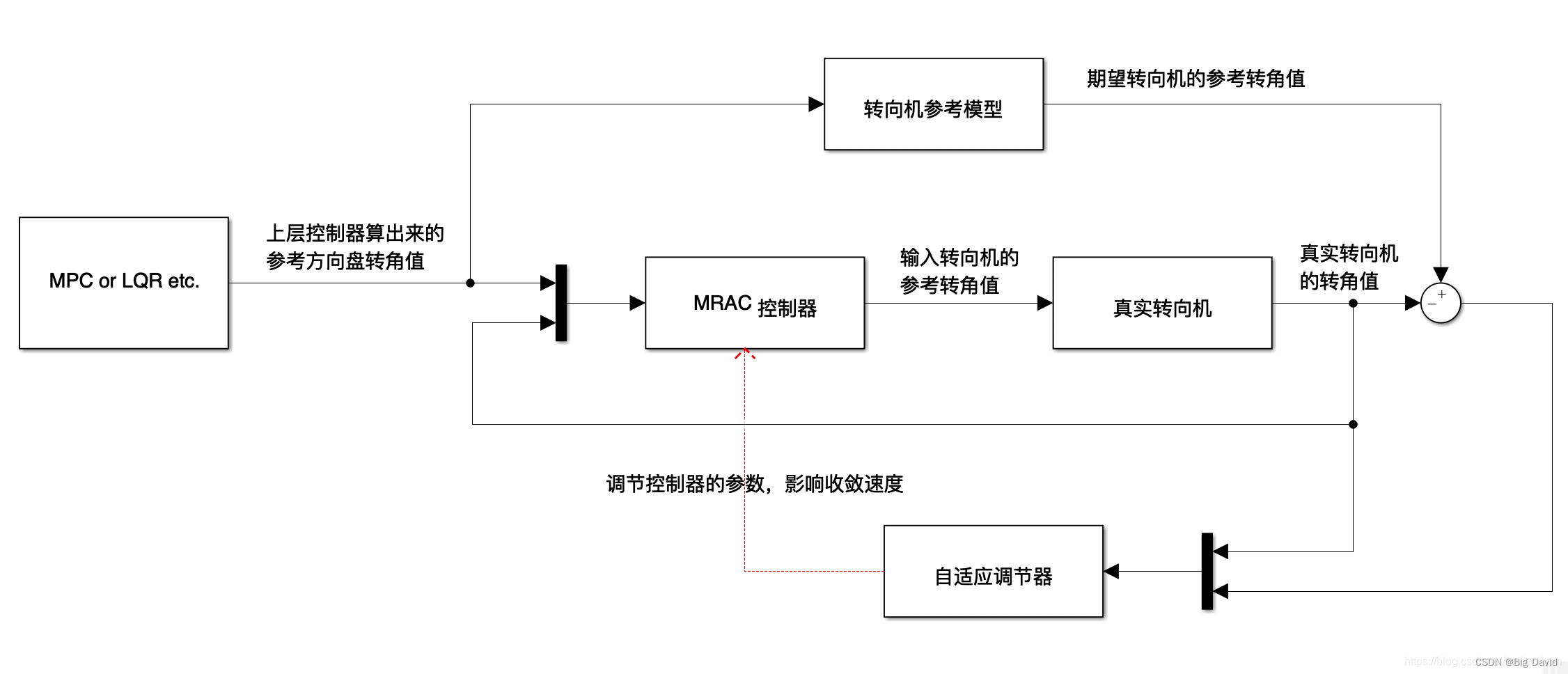 MRAC在无人驾驶控制算法中,往往会和上层控制算法联合起来使用,上层控制算法包含MPC、LQR、Stanley等。一般横向控制算法不会单独使用MRAC控制器,MRAC只是起到一个辅助调节的作用。
MRAC在无人驾驶控制算法中,往往会和上层控制算法联合起来使用,上层控制算法包含MPC、LQR、Stanley等。一般横向控制算法不会单独使用MRAC控制器,MRAC只是起到一个辅助调节的作用。
MRAC控制器收敛的并不是上层控制算法(MPC等)给出的参考方向盘转角值,而是收敛期望转向机算出来的参考转角值,让真实转向机的角度跟随期望转向机的角度。期望转向机的模型就是MRAC算法中的MR(参考模型),期望转向机的系数(阻尼比等)往往是设计者给定的,不一定要是接近于真实转向机,如果参考模型接近于真实模型,反而使得此算法变得没有意义。
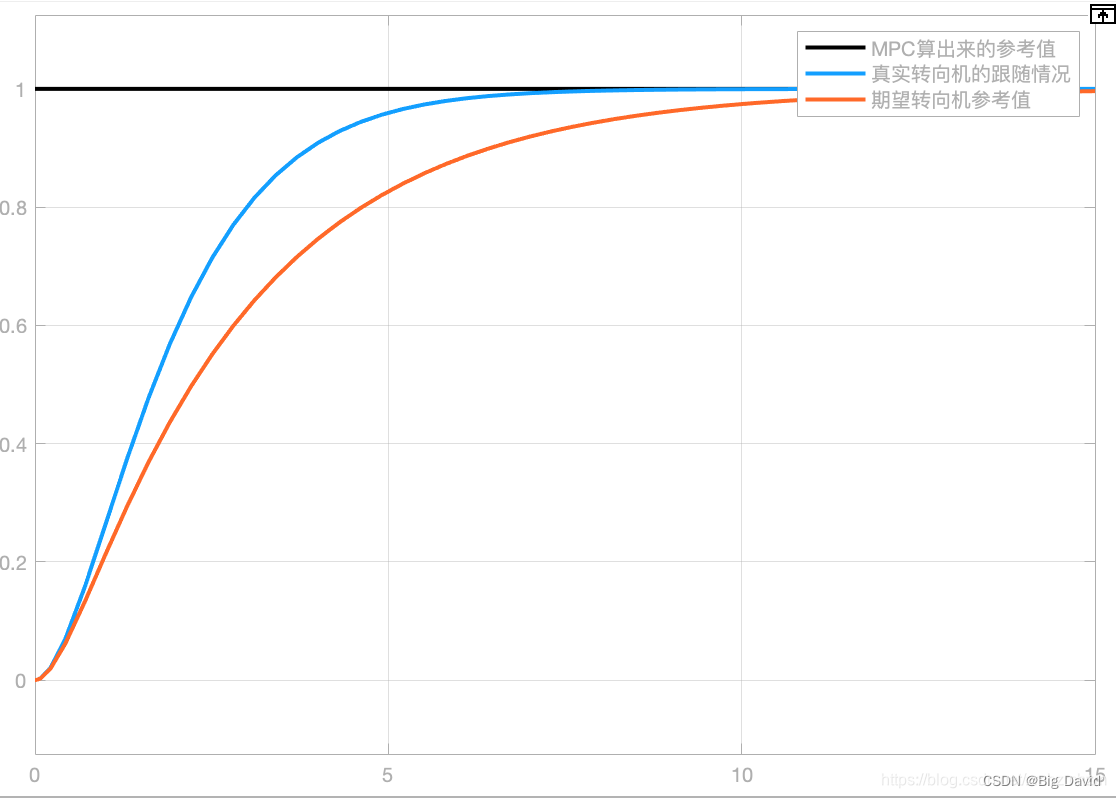 假设黑色线表示这一时刻上层控制算法MPC算出来的方向盘转角期望值,蓝色线代表在无MRAC作用时(单用MPC控制),真实转向机对MPC给出的参考值的跟随情况。而红色线代表是这一时刻用期望的转向机模型算出来的转角期望值。MRAC算法收敛的不是黑色线与蓝色线的误差,而是收敛蓝色线与红色线的误差。
假设黑色线表示这一时刻上层控制算法MPC算出来的方向盘转角期望值,蓝色线代表在无MRAC作用时(单用MPC控制),真实转向机对MPC给出的参考值的跟随情况。而红色线代表是这一时刻用期望的转向机模型算出来的转角期望值。MRAC算法收敛的不是黑色线与蓝色线的误差,而是收敛蓝色线与红色线的误差。
为什么要用MRAC控制器?
为了让同一套上层控制算法(MPC等)在面对不同的真实转向机时,不受硬件参数差异的影响。比如现在有两台车,一台是博世的转向机,一台是国产转向机,两台转向机的阻尼比等系数都不同(模型不同),如果我设计一个期望的转向机参考模型,并用MRAC算法控制的话,那么这两台建模不同的转向机都会变成我设计的期望转向机的模型。这就是模型参考的意义。
设计的期望转向机的模型对信号的收敛速度应该是要低于真实转向机的。因为要使一个收敛快的转向机变得收敛慢是容易实现的,但要使一个收敛慢的转向机变得收敛快,往往难以克服机械硬件的限制
4 一维、二维插值算法
4.1 一维插值算法
interpolation_1d.h
#pragma once#include <memory>
#include <utility>
#include <vector>#include "Eigen/Core"
#include "unsupported/Eigen/Splines"namespace apollo {
namespace control {class Interpolation1D {public:typedef std::vector<std::pair<double, double>> DataType;Interpolation1D() = default;// 初始化bool Init(const DataType& xy);// 仅在[x_min,x_max]之间插值x// 对于超出范围的x,将返回起始或结束y值。double Interpolate(double x) const;private:// 将X值缩小到[0,1]double ScaledValue(double x) const;Eigen::RowVectorXd ScaledValues(Eigen::VectorXd const& x_vec) const;double x_min_ = 0.0;double x_max_ = 0.0;double y_start_ = 0.0;double y_end_ = 0.0;// 一维“点”的样条曲线std::unique_ptr<Eigen::Spline<double, 1>> spline_;
};} // namespace control
} // namespace apollo
interpolation_1d.cc
#include "modules/control/control_component/controller_task_base/common/interpolation_1d.h"#include <algorithm>#include "cyber/common/log.h"namespace apollo {
namespace control {const double kDoubleEpsilon = 1e-6;
// 初始化插值器
bool Interpolation1D::Init(const DataType& xy) {if (xy.empty()) {AERROR << "empty input.";return false;}auto data(xy);std::sort(data.begin(), data.end());Eigen::VectorXd x(data.size());Eigen::VectorXd y(data.size());for (unsigned i = 0; i < data.size(); ++i) {x(i) = data[i].first;y(i) = data[i].second;}x_min_ = data.front().first;x_max_ = data.back().first;y_start_ = data.front().second;y_end_ = data.back().second;// 在此处进行插值拟合。X值需要在此处进行缩放到[0, 1]spline_.reset(new Eigen::Spline<double, 1>(Eigen::SplineFitting<Eigen::Spline<double, 1>>::Interpolate(y.transpose(),// 插值多项式不超过三次,但接受短向量static_cast<Eigen::DenseIndex>(std::min<size_t>(x.size() - 1, 3)),ScaledValues(x))));return true;
}
// 使用插值器进行插值
double Interpolation1D::Interpolate(double x) const {if (x < x_min_) {return y_start_;}if (x > x_max_) {return y_end_;}// 提取插值值时,x值也需要进行缩放return (*spline_)(ScaledValue(x))(0);
}
// x就被转换成了一个0到1之间的值
double Interpolation1D::ScaledValue(double x) const {// 避免除以零的错误if (std::fabs(x_max_ - x_min_) < kDoubleEpsilon) {return x_min_;}return (x - x_min_) / (x_max_ - x_min_);
}
// 原向量中元素经过ScaledValue函数处理后的结果
Eigen::RowVectorXd Interpolation1D::ScaledValues(Eigen::VectorXd const& x_vec) const {return x_vec.unaryExpr([this](double x) { return ScaledValue(x); }).transpose();
}} // namespace control
} // namespace apollo
4.2 二维插值算法
interpolation_2d.h
#pragma once#include <map>
#include <memory>
#include <tuple>
#include <utility>
#include <vector>namespace apollo {
namespace control {
/*** @class Interpolation2D** @brief linear interpolation from key (double, double) to one double value.*/
class Interpolation2D {public:typedef std::vector<std::tuple<double, double, double>> DataType;typedef std::pair<double, double> KeyType;Interpolation2D() = default;bool Init(const DataType &xyz);// 从二维关键点(两个double类型值,通常表示空间中的x和y坐标)到一个double值double Interpolate(const KeyType &xy) const;private:// 一个double到double的映射表,表示z值与y值之间的关系double InterpolateYz(const std::map<double, double> &yz_table,double y) const;// 处理两个值(value_before和value_after)和它们对应的分段距离,计算并返回在给定区间内的插值结果double InterpolateValue(const double value_before, const double dist_before,const double value_after,const double dist_after) const;std::map<double, std::map<double, double>> xyz_;
};} // namespace control
} // namespace apollo
interpolation_2d.cc
#include "modules/control/control_component/controller_task_base/common/interpolation_2d.h"#include <cmath>#include "cyber/common/log.h"namespace {const double kDoubleEpsilon = 1.0e-6;} // namespacenamespace apollo {
namespace control {bool Interpolation2D::Init(const DataType &xyz) {if (xyz.empty()) {AERROR << "empty input.";return false;}// 对于每个元素t,提取其x、y和z坐标for (const auto &t : xyz) {xyz_[std::get<0>(t)][std::get<1>(t)] = std::get<2>(t);}return true;
}
// 函数接收一个键类型(KeyType)的xy参数,用于查找并进行二维空间中的插值计算。这里使用了双线性插值方法
double Interpolation2D::Interpolate(const KeyType &xy) const {// 获取数据集中最大和最小的x值,加上一个很小的容差kDoubleEpsilon防止比较时的精度问题double max_x = xyz_.rbegin()->first;double min_x = xyz_.begin()->first;// 如果输入的x值大于等于最大x减去一个小误差,表示接近最高点,进行y-z方向的插值if (xy.first >= max_x - kDoubleEpsilon) {return InterpolateYz(xyz_.rbegin()->second, xy.second);}// 同理,如果输入的x值小于等于最小x加上小误差,表示接近最低点,进行y-z方向的插值if (xy.first <= min_x + kDoubleEpsilon) {return InterpolateYz(xyz_.begin()->second, xy.second);}// 在数据集中找到输入x值对应的索引之后的元素(近似大于等于的元素)auto itr_after = xyz_.lower_bound(xy.first);// 同样找到索引之前的元素(近似小于的元素)auto itr_before = itr_after;// 如果不是第一个元素,则向前移动一位if (itr_before != xyz_.begin()) {--itr_before;}// 计算输入x值前后的z值double x_before = itr_before->first;double z_before = InterpolateYz(itr_before->second, xy.second);double x_after = itr_after->first;double z_after = InterpolateYz(itr_after->second, xy.second);// 计算输入x值与前两个x值之间的差double x_diff_before = std::fabs(xy.first - x_before);double x_diff_after = std::fabs(xy.first - x_after);// 最后使用差值和对应的z值执行双线性插值return InterpolateValue(z_before, x_diff_before, z_after, x_diff_after);
}double Interpolation2D::InterpolateYz(const std::map<double, double> &yz_table,double y) const {if (yz_table.empty()) {AERROR << "Unable to interpolateYz because yz_table is empty.";return y;}double max_y = yz_table.rbegin()->first;double min_y = yz_table.begin()->first;if (y >= max_y - kDoubleEpsilon) {return yz_table.rbegin()->second;}if (y <= min_y + kDoubleEpsilon) {return yz_table.begin()->second;}auto itr_after = yz_table.lower_bound(y);auto itr_before = itr_after;if (itr_before != yz_table.begin()) {--itr_before;}double y_before = itr_before->first;double z_before = itr_before->second;double y_after = itr_after->first;double z_after = itr_after->second;double y_diff_before = std::fabs(y - y_before);double y_diff_after = std::fabs(y - y_after);return InterpolateValue(z_before, y_diff_before, z_after, y_diff_after);
}
// 二维插值函数
double Interpolation2D::InterpolateValue(const double value_before,const double dist_before,const double value_after,const double dist_after) const {// 如果前一个点到目标点的距离小于一个很小的阈值,则直接返回前一个点的值,避免除零错误 if (dist_before < kDoubleEpsilon) {return value_before;}// 如果后一个点到目标点的距离小于一个很小的阈值,则直接返回后一个点的值,避免除零错误if (dist_after < kDoubleEpsilon) {return value_after;}// 计算前一个点与后一个点之间的值的差距double value_gap = value_after - value_before;// 根据距离权重计算插值的中间值double value_buff = value_gap * dist_before / (dist_before + dist_after);// 返回插值结果return value_before + value_buff;
}} // namespace control
} // namespace apollo
相关文章:

Apollo9.0 PNC源码学习之Control模块(二)
前面文章:Apollo9.0 PNC源码学习之Control模块(一) 本文将对具体控制器以及原理做一个剖析 1 PID控制器 1.1 PID理论基础 如下图所示,PID各参数(Kp,Ki,Kd)的作用: 任何闭环控制系统的首要任务是要稳、准、快的响…...

直线度测量仪发展历程!
直线度测量仪的发展历程可以概括为以下几个关键阶段: 拉钢丝法: 早期直线度测量的简单直观方法,利用钢丝受重力自然下垂的原理来测量直线度误差。 随着机械设备的大型化和测量精度要求的提高,该方法逐渐无法满足要求,正…...
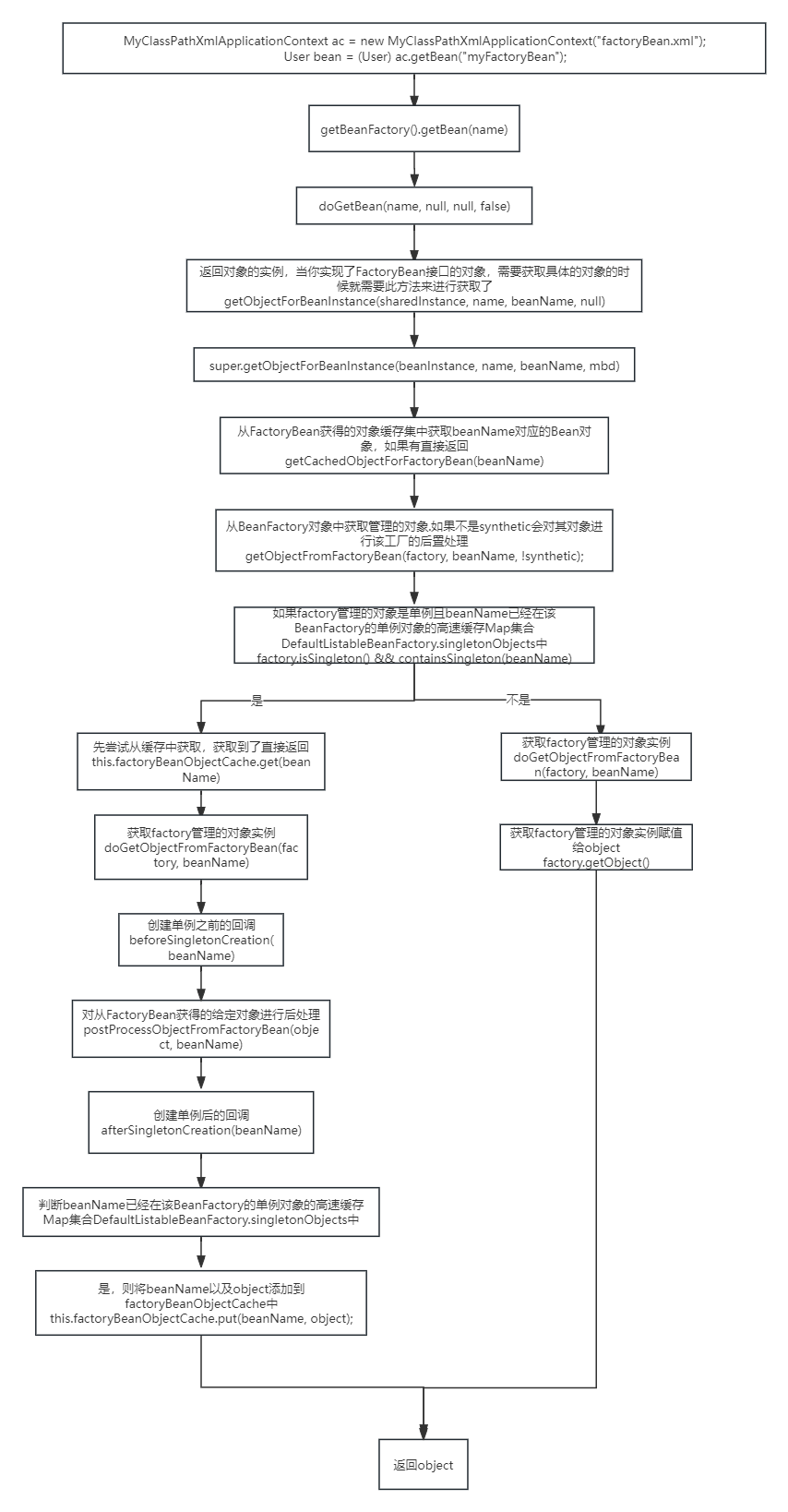
09-spring的bean创建流程(一)
文章目录 spring中bean的创建流程finishBeanFactoryInitialization(beanFactory)beanFactory.preInstantiateSingletons();getMergedLocalBeanDefinition(beanName);流程实现FactoryBean接口,里面的对象实例化过程 spring中bean的创建流程 finishBeanFactoryInitialization(be…...

spring中基于setting和构造器的注入方式
Spring中可以通过setting和构造器两种方式进行依赖注入。 1.基于setting的注入方式(Setter Injection): 实现方式:在类中添加对应的属性以及对应的setter方法,在配置文件中使用<property>元素进行注入。 示例代码…...

爬虫基本原理?介绍|实现|问题解决
爬虫基本原理: 模拟用户行为: 网络爬虫(Web Crawler)是一种自动化的程序,它模拟人类用户访问网站的方式,通过发送HTTP/HTTPS请求到服务器以获取网页内容。 请求与响应: 爬虫首先构建并发送带有…...
)
DevOps的原理及应用详解(六)
本系列文章简介: 在当今快速变化的商业环境中,企业对于软件交付的速度、质量和安全性要求日益提高。传统的软件开发和运维模式已经难以满足这些需求,因此,DevOps(Development和Operations的组合)应运而生&a…...
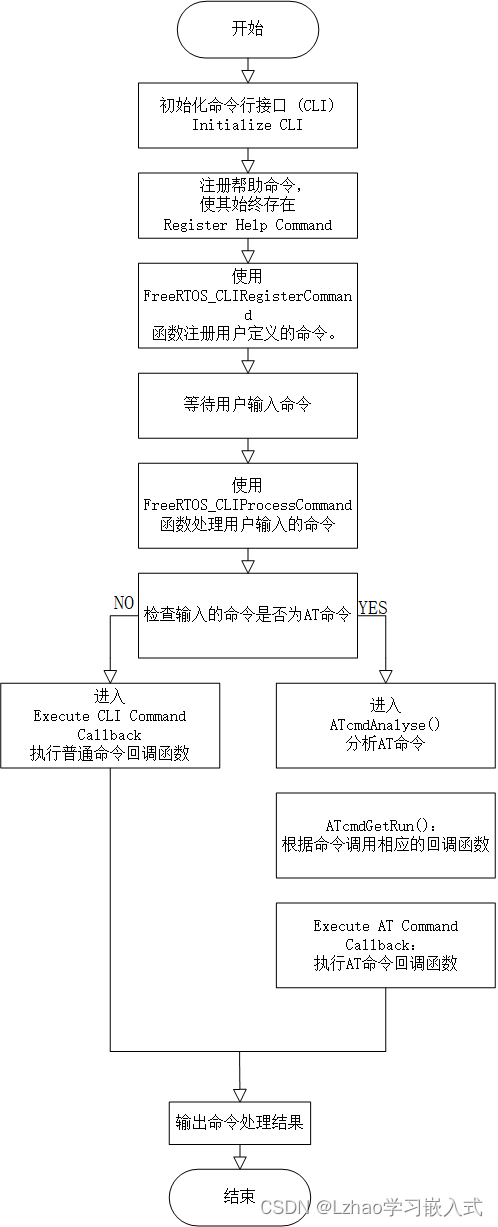
手撸 串口交互命令行 及 AT应用层协议解析框架
在嵌入式系统开发中,命令行接口(CLI)和AT命令解析是常见的需求。CLI提供了方便的调试接口,而AT命令则常用于模块间的通信控制。本文将介绍如何手动实现一个串口交互的命令行及AT应用层协议解析框架,适用于FreeRTOS系统…...

Redis几种部署模式介绍
Redis 提供了几种不同的部署模式,以满足不同的使用场景和可用性需求。这些模式包括单机模式、主从复制、哨兵模式和集群模式。下面我将简要介绍每种模式的特点和用途: 单机模式: 描述:单个 Redis 服务器实例运行在一台机器上&…...
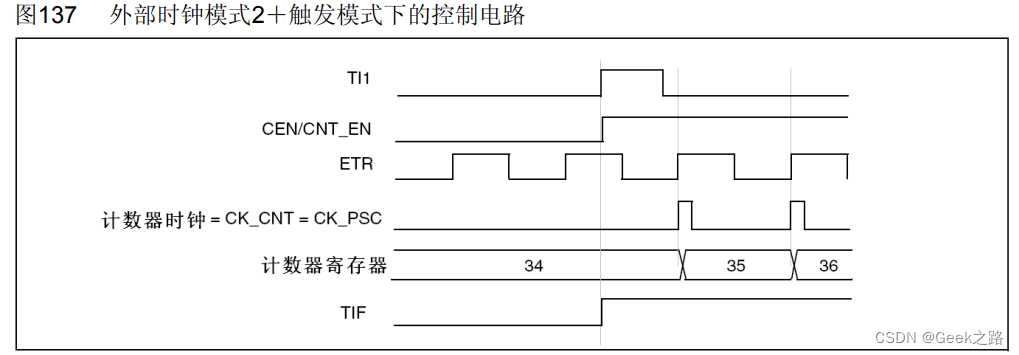
【STM32HAL库学习】定时器功能、时钟以及各种模式理解
一、文章目的 记录自己从学习了定时器理论->代码实现使用定时->查询数据手册,加深了对定时器的理解以及该过程遇到了的一些不清楚的知识。 上图为参考手册里通用定时器框图,关于定时器各种情况的工作都在上面了,在理论学习和实际应用后…...

3588麒麟系统硬解码实战
目录 安装rockchip-mpp deb 查找头文件 .pro文件添加 检查库是否已安装 error: stdlib.h: No such file or directory ffmpeg 查找ffmpeg路径: 查找FFmpeg库和头文件的位置 使用pkg-config工具查找FFmpeg路径 ok的ffmpeg配置: ffmpeg查看是否支持libx264 ffmpeg …...

十二 nginx中location重写和匹配规则
十二 location匹配规则 ^~ ~ ~* !~ !~* /a / 内部服务跳转 十三 nginx地址重写rewrite if rewrite set return 13.1 if 应用环境 server location -x 文件是否可执行 $args $document_rot $host $limit_rate $remote_addr $server_name $document_uri if …...

python的视频处理FFmpeg库使用
FFmpeg 是一个强大的多媒体处理工具,用于录制、转换和流式传输音频和视频。它支持几乎所有的音频和视频格式,并且可以在各种平台上运行。FFmpeg 在 Python 中的使用可以通过调用其命令行工具或使用专门的库如 ffmpeg-python。以下是详细介绍如何在 Python 中使用 FFmpeg,包括…...

接口测试时, 数据Mock为何如此重要?
一、为什么要mock 工作中遇到以下问题,我们可以使用mock解决: 1、无法控制第三方系统某接口的返回,返回的数据不满足要求 2、某依赖系统还未开发完成,就需要对被测系统进行测试 3、有些系统不支持重复请求,或有访问…...

未授权与绕过漏洞
1、Laravel Framework 11 - Credential Leakage(CVE-2024-29291)认证泄漏 导航这个路径storage/logs/laravel.log搜索以下信息: PDO->__construct(mysql:host 2、 Flowise 1.6.5 - Authentication Bypass(CVE-2024-31621&am…...

云原生周刊:Kubernetes 十周年 | 2024.6.11
开源项目推荐 Kubernetes Goat Kubernetes Goat 是一个故意设计成有漏洞的 Kubernetes 集群环境,旨在通过交互式实践场地来学习并练习 Kubernetes 安全性。 kube-state-metrics (KSM) kube-state-metrics 是一个用于收集 Kubernetes 集群状态信息的开源项目&…...
ClickHouse内幕(1)数据存储与过滤机制
本文主要讲述ClickHouse中的数据存储结构,包括文件组织结构和索引结构,以及建立在其基础上的数据过滤机制,从Part裁剪到Mark裁剪,最后到基于SIMD的行过滤机制。 数据过滤机制实质上是构建在数据存储格式之上的算法,所…...

1.Mongodb 介绍及部署
MongoDB 是一个开源的文档导向数据库,采用NoSQL(非关系型数据库)的设计理念。MongoDB是一个基于分布式文件存储的数据库。 分布式文件存储是一种将文件数据分布式的存储在多台计算机上。MongoDB是一款强大的文档导向数据库,适合处…...

Java 技巧:如何获取字符串中最后一个英文逗号后面的内容
在日常的Java编程中,处理字符串是非常常见的任务之一。有时我们需要从一个字符串中截取特定部分,例如获取最后一个英文逗号后的内容。这篇文章将详细介绍如何使用Java来实现这一需求,并提供一个示例代码来演示其实现过程。 需求分析 假设我们…...
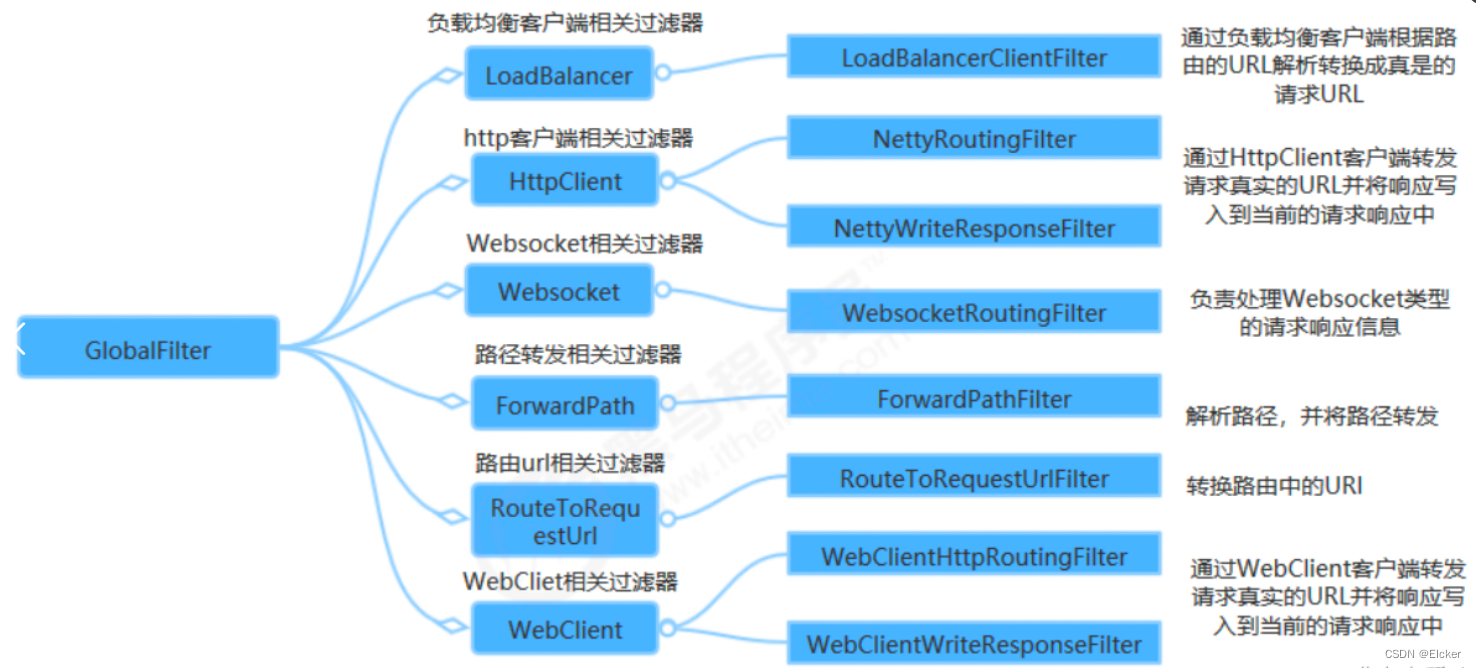
玩转微服务-GateWay
目录 一. 背景二. API网关1. 概念2. API网关定义3. API网关的四大职能4. API网关分类5. 开源API网关介绍6. 开源网关的选择 三. Spring Cloud Gateway1. 文档地址2. 三个核心概念3. 工作流程4. 运行原理4.1 路由原理4.2 RouteLocator 5. Predicate 断言6. 过滤器 Filter6.1. 过…...

Amortized bootstrapping via Automorphisms
参考文献: [MS18] Micciancio D, Sorrell J. Ring packing and amortized FHEW bootstrapping. ICALP 2018: 100:1-100:14.[GPV23] Guimares A, Pereira H V L, Van Leeuwen B. Amortized bootstrapping revisited: Simpler, asymptotically-faster, implemented. …...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
