Shell脚本要点和难点以及具体应用和优缺点介绍
Shell 脚本是一种用于自动化任务和简化常见系统命令的脚本语言,通常运行在 Unix 或 Unix-like 的系统上,如 Linux 和 macOS。Shell 脚本可以直接在命令行中执行,也可以保存为文件并通过 bash、sh、zsh 等 shell 解释器来执行。
以下是一个简单的 Shell 脚本示例,它演示了如何打印一条消息、读取用户输入并计算两个数字的和:
bash
#!/bin/bash
# 这是一个简单的 Shell 脚本示例
# 打印一条消息
echo "Hello, World!"
# 读取用户输入的两个数字
read -p "请输入第一个数字: " num1
read -p "请输入第二个数字: " num2
# 计算两个数字的和
sum=$(($num1 + $num2))
# 打印结果
echo "两个数字的和是: $sum"
要运行这个脚本,你需要:
将上述代码保存为一个文件,例如 example.sh。
在文件的第一行添加 #!/bin/bash(这被称为 shebang 或 hashbang),它告诉系统使用哪个解释器来执行脚本。在这个例子中,我们使用的是 bash。
给予脚本执行权限。在命令行中,使用 chmod +x example.sh 命令。
执行脚本。在命令行中,输入 ./example.sh 并按回车。
注意:在某些系统上,你可能需要指定 bash 的完整路径,如 #!/usr/bin/env bash,以确保脚本在不
相关文章:

Shell脚本要点和难点以及具体应用和优缺点介绍
Shell 脚本是一种用于自动化任务和简化常见系统命令的脚本语言,通常运行在 Unix 或 Unix-like 的系统上,如 Linux 和 macOS。Shell 脚本可以直接在命令行中执行,也可以保存为文件并通过 bash、sh、zsh 等 shell 解释器来执行。 以下是一个简单的 Shell 脚本示例,它演示了如…...

移动端浏览器的扫描二维码实现(vue-qrcode-reader与jsQR方式)
1. 实现功能 类似扫一扫的功能,自动识别到画面中的二维码并进行识别,也可以选择从相册中上传。 2. 涉及到的一些插件介绍 vue-qrcode-reader 一组用于检测和解码二维码的Vue.js组件 jsQR 一个纯粹的javascript二维码阅读库,该库接收原始…...

android中调用onnxruntime框架
创建空白项目 安装Android Studio及创建空白项目参考:【安卓Java原生开发学习记录】一、安卓开发环境的搭建与HelloWorld(详细图文解释)_安卓原生开发-CSDN博客 切记:build configuration language 一定选择Groovy!官…...
【机器学习】与【数据挖掘】技术下【C++】驱动的【嵌入式】智能系统优化
目录 一、嵌入式系统简介 二、C在嵌入式系统中的优势 三、机器学习在嵌入式系统中的挑战 四、C实现机器学习模型的基本步骤 五、实例分析:使用C在嵌入式系统中实现手写数字识别 1. 数据准备 2. 模型训练与压缩 3. 模型部署 六、优化与分析 1. 模型优化 模…...
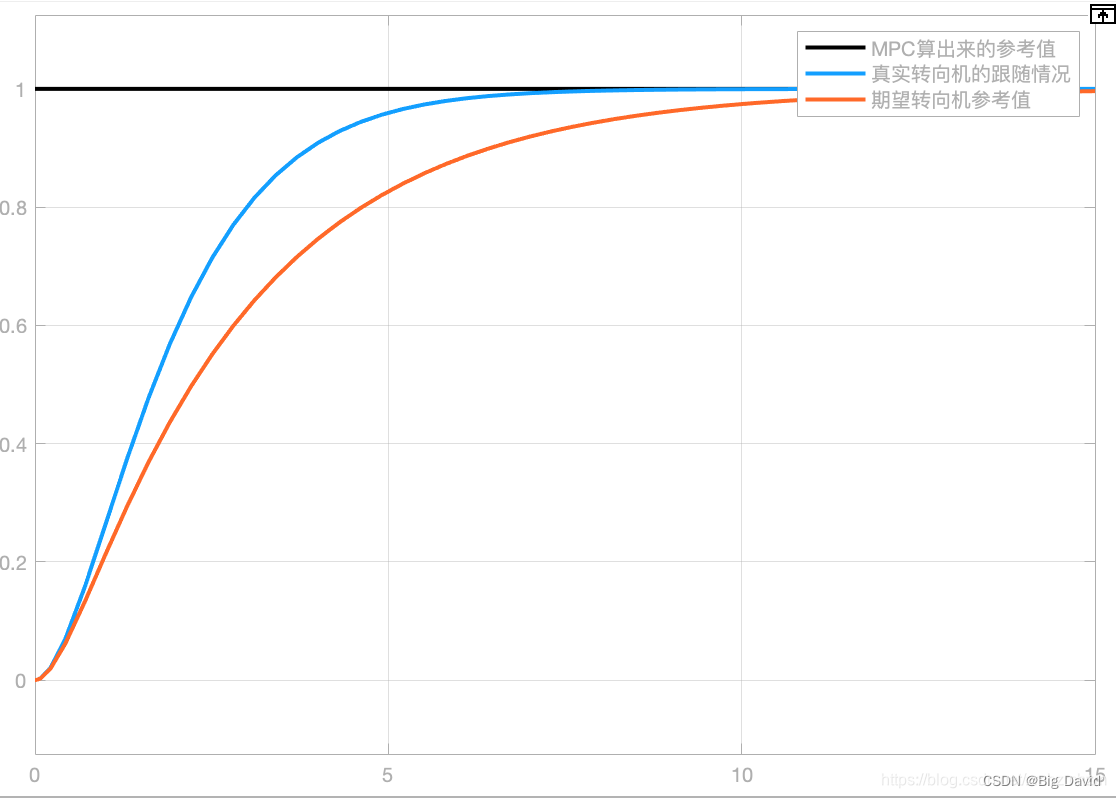
Apollo9.0 PNC源码学习之Control模块(二)
前面文章:Apollo9.0 PNC源码学习之Control模块(一) 本文将对具体控制器以及原理做一个剖析 1 PID控制器 1.1 PID理论基础 如下图所示,PID各参数(Kp,Ki,Kd)的作用: 任何闭环控制系统的首要任务是要稳、准、快的响…...

直线度测量仪发展历程!
直线度测量仪的发展历程可以概括为以下几个关键阶段: 拉钢丝法: 早期直线度测量的简单直观方法,利用钢丝受重力自然下垂的原理来测量直线度误差。 随着机械设备的大型化和测量精度要求的提高,该方法逐渐无法满足要求,正…...
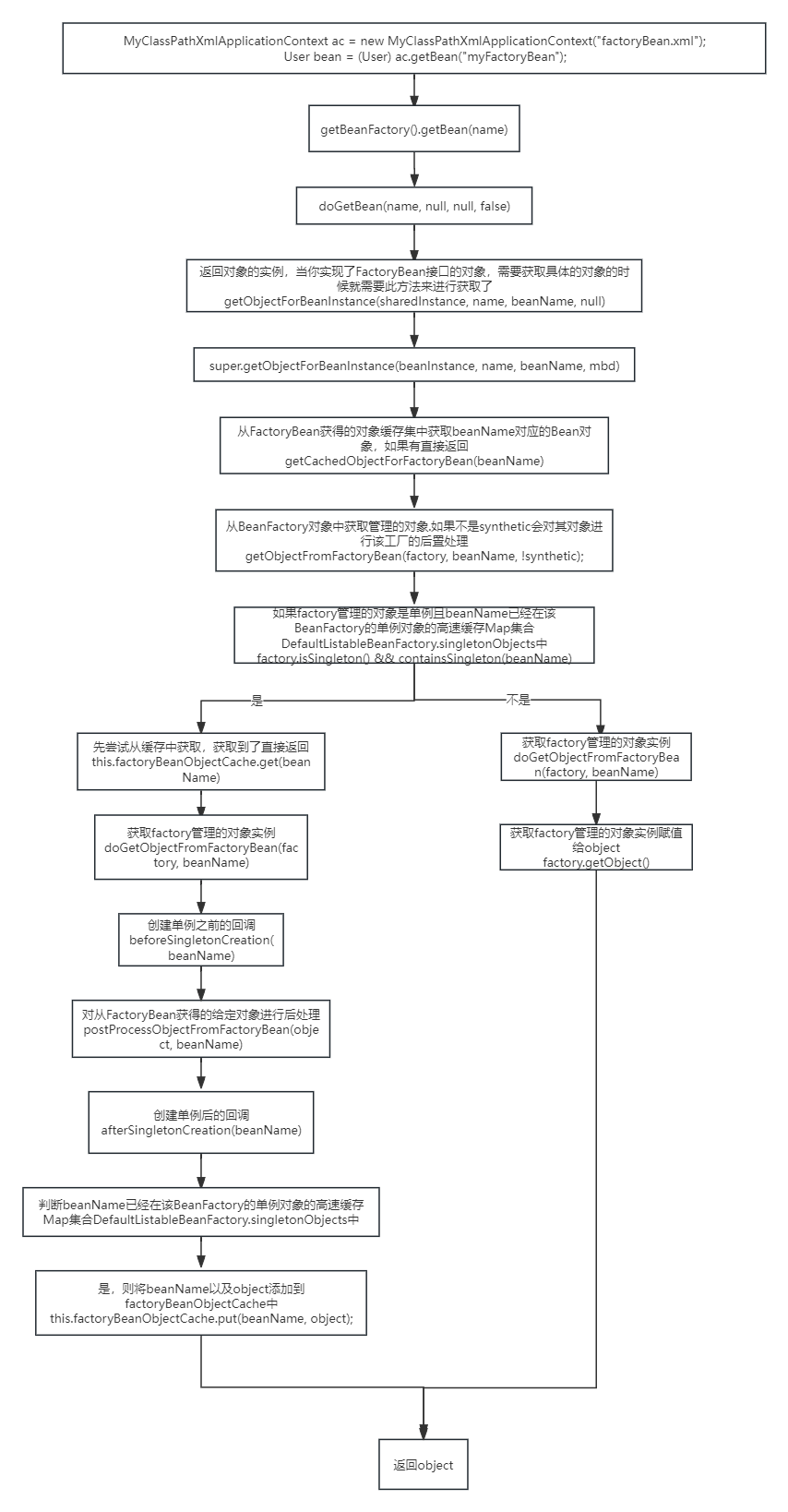
09-spring的bean创建流程(一)
文章目录 spring中bean的创建流程finishBeanFactoryInitialization(beanFactory)beanFactory.preInstantiateSingletons();getMergedLocalBeanDefinition(beanName);流程实现FactoryBean接口,里面的对象实例化过程 spring中bean的创建流程 finishBeanFactoryInitialization(be…...

spring中基于setting和构造器的注入方式
Spring中可以通过setting和构造器两种方式进行依赖注入。 1.基于setting的注入方式(Setter Injection): 实现方式:在类中添加对应的属性以及对应的setter方法,在配置文件中使用<property>元素进行注入。 示例代码…...

爬虫基本原理?介绍|实现|问题解决
爬虫基本原理: 模拟用户行为: 网络爬虫(Web Crawler)是一种自动化的程序,它模拟人类用户访问网站的方式,通过发送HTTP/HTTPS请求到服务器以获取网页内容。 请求与响应: 爬虫首先构建并发送带有…...
)
DevOps的原理及应用详解(六)
本系列文章简介: 在当今快速变化的商业环境中,企业对于软件交付的速度、质量和安全性要求日益提高。传统的软件开发和运维模式已经难以满足这些需求,因此,DevOps(Development和Operations的组合)应运而生&a…...
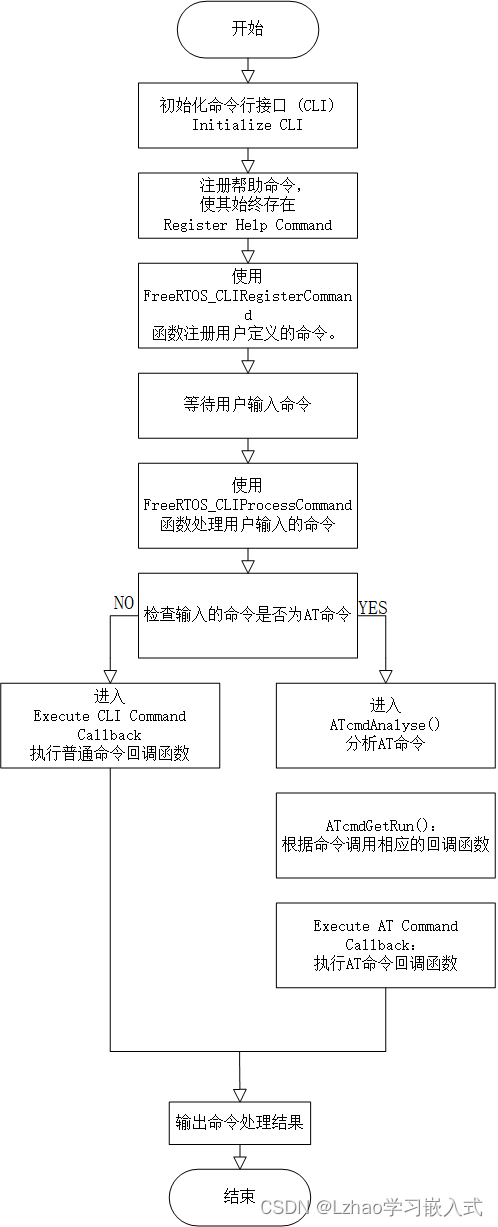
手撸 串口交互命令行 及 AT应用层协议解析框架
在嵌入式系统开发中,命令行接口(CLI)和AT命令解析是常见的需求。CLI提供了方便的调试接口,而AT命令则常用于模块间的通信控制。本文将介绍如何手动实现一个串口交互的命令行及AT应用层协议解析框架,适用于FreeRTOS系统…...

Redis几种部署模式介绍
Redis 提供了几种不同的部署模式,以满足不同的使用场景和可用性需求。这些模式包括单机模式、主从复制、哨兵模式和集群模式。下面我将简要介绍每种模式的特点和用途: 单机模式: 描述:单个 Redis 服务器实例运行在一台机器上&…...
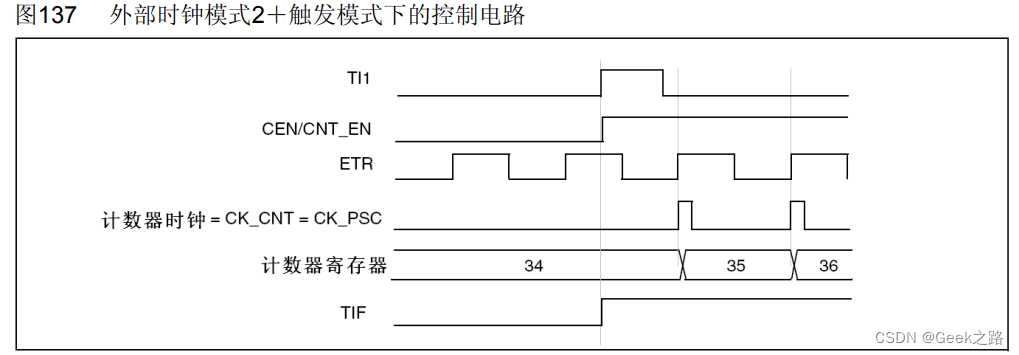
【STM32HAL库学习】定时器功能、时钟以及各种模式理解
一、文章目的 记录自己从学习了定时器理论->代码实现使用定时->查询数据手册,加深了对定时器的理解以及该过程遇到了的一些不清楚的知识。 上图为参考手册里通用定时器框图,关于定时器各种情况的工作都在上面了,在理论学习和实际应用后…...

3588麒麟系统硬解码实战
目录 安装rockchip-mpp deb 查找头文件 .pro文件添加 检查库是否已安装 error: stdlib.h: No such file or directory ffmpeg 查找ffmpeg路径: 查找FFmpeg库和头文件的位置 使用pkg-config工具查找FFmpeg路径 ok的ffmpeg配置: ffmpeg查看是否支持libx264 ffmpeg …...

十二 nginx中location重写和匹配规则
十二 location匹配规则 ^~ ~ ~* !~ !~* /a / 内部服务跳转 十三 nginx地址重写rewrite if rewrite set return 13.1 if 应用环境 server location -x 文件是否可执行 $args $document_rot $host $limit_rate $remote_addr $server_name $document_uri if …...

python的视频处理FFmpeg库使用
FFmpeg 是一个强大的多媒体处理工具,用于录制、转换和流式传输音频和视频。它支持几乎所有的音频和视频格式,并且可以在各种平台上运行。FFmpeg 在 Python 中的使用可以通过调用其命令行工具或使用专门的库如 ffmpeg-python。以下是详细介绍如何在 Python 中使用 FFmpeg,包括…...

接口测试时, 数据Mock为何如此重要?
一、为什么要mock 工作中遇到以下问题,我们可以使用mock解决: 1、无法控制第三方系统某接口的返回,返回的数据不满足要求 2、某依赖系统还未开发完成,就需要对被测系统进行测试 3、有些系统不支持重复请求,或有访问…...

未授权与绕过漏洞
1、Laravel Framework 11 - Credential Leakage(CVE-2024-29291)认证泄漏 导航这个路径storage/logs/laravel.log搜索以下信息: PDO->__construct(mysql:host 2、 Flowise 1.6.5 - Authentication Bypass(CVE-2024-31621&am…...

云原生周刊:Kubernetes 十周年 | 2024.6.11
开源项目推荐 Kubernetes Goat Kubernetes Goat 是一个故意设计成有漏洞的 Kubernetes 集群环境,旨在通过交互式实践场地来学习并练习 Kubernetes 安全性。 kube-state-metrics (KSM) kube-state-metrics 是一个用于收集 Kubernetes 集群状态信息的开源项目&…...
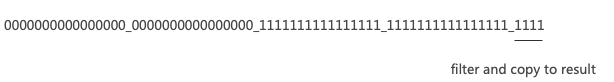
ClickHouse内幕(1)数据存储与过滤机制
本文主要讲述ClickHouse中的数据存储结构,包括文件组织结构和索引结构,以及建立在其基础上的数据过滤机制,从Part裁剪到Mark裁剪,最后到基于SIMD的行过滤机制。 数据过滤机制实质上是构建在数据存储格式之上的算法,所…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...
