Autoformer
A u t o f o r m e r Autoformer Autoformer
摘要
我们设计了 A u t o f o r m e r Autoformer Autoformer作为一种新型分解架构,带有自相关机制。我们打破了序列分解的预处理惯例,并将其革新为深度模型的基本内部模块。这种设计使 A u t o f o r m e r Autoformer Autoformer具备了对复杂时间序列的渐进分解能力。进一步地,受随机过程理论的启发,我们基于序列周期性设计了自相关机制,它在子序列级别进行依赖关系的发现和表示聚合。在效率和准确性方面,自相关机制都优于自注意力机制。
1.简介
最近的深度预测模型已经取得了很大的进展,特别是基于变压器的模型。得益于自关注机制,变压器在对序列数据的长期依赖关系建模方面具有很大的优势,这使得更强大的大模型成为可能。我们尝试利用序列的周期性来更新自关注中的点向连接。观察到,周期之间处于相同相位位置的子序列往往呈现相似的时间过程。因此,尝试基于序列周期性导出的过程相似性构建一个序列级连接。
提出了一个原始的自耦器来代替变压器进行长期时间序列预测。自耦器仍然沿用残差和编解码器结构,但将变压器改造为分解预测结构。通过嵌入我们提出的分解块作为内部算子,自耦器器可以逐步从预测的隐藏变量中分离出长期趋势信息。这种设计允许我们的模型在预测过程中交替分解和细化中间结果。受随机过程理论的启发,自耦器引入了自相关机制来代替自关注,该机制基于序列的周期性发现子序列的相似性,并从底层周期中聚合相似的子序列。这种序列智能机制为长度为 L L L的序列实现了 O ( L l o g L ) O(L log L) O(LlogL)复杂度,并通过将逐点表示聚合扩展到子序列级别来打破信息利用瓶颈。自耦器在六个基准上达到了最先进的精度。贡献总结如下:
- 为了解决长期未来复杂的时间模式,我们提出了自耦器作为一个分解架构,并设计了内部分解块,以赋予深度预测模型具有内在的渐进分解能力。
- 我们提出了一种自相关机制,在序列级别上具有依赖性发现和信息聚合。我们的机制超越了以前的自关注家族,可以同时有利于计算效率和信息利用率。
- 在六个基准的长期设定下,自耦器实现了38%的相对改进,涵盖了五个实际应用:能源、交通、经济、天气和疾病。
2.相关工作
- 提出的自相关机制基于时间序列的固有周期性,可以提供序列明智的连接。
- 自耦器利用分解作为深度模型的内部块,可以在整个预测过程中逐步分解隐藏序列,包括过去的序列和预测的中间结果。
3.Autoformer

将 T r a n s f o r m e r Transformer Transformer改造为一个深度分解架构,包括内部的系列分解块、自相关机制以及相应的编码器和解码器。
序列分解模块:
该模块的目的是将输入的时间序列分解为趋势周期部分和季节性部分,以便更好地进行长期预测。由于未来是未知的,因此该模块通过对预测的中间隐藏变量进行处理来提取长期稳定的趋势。具体方法是使用移动平均法,通过填充操作保持序列长度不变。最终,该模块输出分解后的季节性部分和趋势周期部分。
采用移动平均法来平滑周期性波动,并突出长期趋势。对于长度为 L L L的输入序列 X ∈ R L × d X \in \mathbb{R}^{L \times d} X∈RL×d,其过程如下:
X t = AvgPool ( Padding ( X ) ) X s = X − X t 方程一 X_t = \text{AvgPool}(\text{Padding}(X))\\ X_s = X - X_t\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\方程一 Xt=AvgPool(Padding(X))Xs=X−Xt 方程一
其中, X s X_s Xs和 X t ∈ R L × d X_t ∈ \mathbb{R}^{L \times d} Xt∈RL×d分别表示季节性和提取的趋势周期部分。我们采用带有填充操作的 A v g P o o l ( ⋅ ) AvgPool(·) AvgPool(⋅)进行移动平均,以保持序列长度不变。我们用 X s , X t = S e r i e s D e c o m p ( X ) Xs, Xt = SeriesDecomp(X) Xs,Xt=SeriesDecomp(X)来总结上述方程,这是一个模型内部模块。
模型输入
编码器的输入是过去 I I I个时间步的 X e n ∈ R I × d Xen ∈ R^{I×d} Xen∈RI×d。作为一个分解架构, A u t o f o r m e r Autoformer Autoformer解码器的输入包含两部分:季节性部分 X d e s ∈ R ( I / 2 + O ) × d X_{des} ∈ R^{(I/2+O)×d} Xdes∈R(I/2+O)×d和趋势周期部分 X d e t ∈ R ( I / 2 + O ) × d X_{det} ∈ R^{(I/2+O)×d} Xdet∈R(I/2+O)×d,这些部分需要被细化。每个初始化包含两部分:一部分是从编码器输入 X e n X_{en} Xen的后半部分(长度为 I / 2 I/2 I/2)分解得到的组件以提供近期信息,另一部分是长度为 O O O的占位符,用标量填充。具体数学公式如下:
Xens , Xent = SeriesDecomp ( Xen I 2 : I ) Xdes = Concat ( Xens , X 0 ) Xdet = Concat ( Xent , XMean ) 方程二 \begin{align*} \text{Xens}, \text{Xent} &= \text{SeriesDecomp}(\text{Xen}_{\frac{I}{2}:I}) \\ \text{Xdes} &= \text{Concat}(\text{Xens}, \text{X}_0) \\ \text{Xdet} &= \text{Concat}(\text{Xent}, \text{XMean}) \end{align*}\ \ \ \ \ \ \ \ \ \ \ \ \ 方程二 Xens,XentXdesXdet=SeriesDecomp(Xen2I:I)=Concat(Xens,X0)=Concat(Xent,XMean) 方程二
其中, X e n s , X e n t ∈ R I / 2 × d X_{ens}, X_{ent} ∈ R^{I/2×d} Xens,Xent∈RI/2×d分别表示 X e n X_{en} Xen的季节性和趋势周期部分,而 X 0 , X M e a n ∈ R O × d X_0, X_{Mean} ∈ R^{O×d} X0,XMean∈RO×d分别表示用零填充的占位符和 X e n X_{en} Xen的均值。
编码器
编码器专注于季节性部分的建模。编码器的输出包含过去的季节性信息,并将作为交叉信息来帮助解码器细化预测结果。假设我们有 N N N个编码器层。第 l l l个编码器层的整体方程可以总结为 X l en = Encoder ( X l − 1 en ) X_l^{\text{en}} = \text{Encoder}(X_{l-1}^{\text{en}}) Xlen=Encoder(Xl−1en)。具体细节如下:
S e n l , 1 , ‾ = S e r i e s D e c o m p ( A u t o − C o r r e l a t i o n ( X e n l − 1 ) + X e n l − 1 ) S e n l , 2 , ‾ = S e r i e s D e c o m p ( F e e d F o r w a r d ( S e n l , 1 ) + S e n l , 1 ) 方程三 S_{en}^{l,1},\underline{}=SeriesDecomp(Auto-Correlation(X_{en}^{l-1})+X_{en}^{l-1})\\S_{en}^{l,2},\underline{}=SeriesDecomp(FeedForward(S_{en}^{l,1})+S_{en}^{l,1}) \ \ \ \ \ 方程三 Senl,1,=SeriesDecomp(Auto−Correlation(Xenl−1)+Xenl−1)Senl,2,=SeriesDecomp(FeedForward(Senl,1)+Senl,1) 方程三
其中, ′ ‾ ′ '\underline\ \ ' ′ ′表示被消除的趋势部分。 X e n l X_{en}^l Xenl是第 l l l个编码器层的输出, X e n 0 X_{en}^0 Xen0是 X e n X_{en} Xen的嵌入表示。 S e n l , i , i ∈ { 1 , 2 } S_{en}^{l,i},i∈\{1,2\} Senl,i,i∈{1,2},分别表示第 l l l层中第 i i i个序列分解块之后的季节性组件。我们将在下一节中详细描述 A u t o − C o r r e l a t i o n ( ⋅ ) Auto-Correlation(·) Auto−Correlation(⋅),它可以无缝地替代自注意力机制。
解码器
解码器包含两个部分:用于趋势周期分量的累积结构,以及用于季节组分的堆叠自相关机制。每个解码器层都包含内部自相关和编码器-解码器自相关,这可以分别细化预测并利用过去的季节信息。模型在解码过程中从中间的隐藏变量中提取潜在趋势,允许 A u t o f o r m e r Autoformer Autoformer逐步细化趋势预测,并消除在自相关中发现基于周期的依赖关系时的干扰信息。假设有 M M M个解码器层。利用来自编码器的潜变量 X e n N X_{en}^N XenN,第 l l l个解码器层的方程可以总结为 X d e l = D e c o d e r ( X d e l − 1 , X e n N ) X_{de}^l=Decoder(X_{de}^{l-1},X_{en}^N) Xdel=Decoder(Xdel−1,XenN)。解码器可以形式化如下:
S l , 1 d e , T l , 1 d e = SeriesDecomp (Auto-Correlation ( X l − 1 d e ) + X l − 1 d e ) S l , 2 d e , T l , 2 d e = SeriesDecomp (Auto-Correlation ( S l , 1 d e , X N e n ) + S l , 1 d e ) S l , 3 d e , T l , 3 d e = SeriesDecomp (FeedForward ( S l , 2 d e ) + S l , 2 d e ) T l d e = T l − 1 d e + W l , 1 ∗ T l , 1 d e + W l , 2 ∗ T l , 2 d e + W l , 3 ∗ T l , 3 d e 方程四 \begin{align*} S_{l,1}^{de}, T_{l,1}^{de} &= \text{SeriesDecomp (Auto-Correlation}(X_{l-1}^{de})+X_{l-1}^{de}) \\ S_{l,2}^{de}, T_{l,2}^{de} &= \text{SeriesDecomp (Auto-Correlation}(S_{l,1}^{de},X_N^{en})+S_{l,1}^{de}) \\ S_{l,3}^{de}, T_{l,3}^{de} &= \text{SeriesDecomp (FeedForward}(S_{l,2}^{de})+S_{l,2}^{de}) \\ T_{l}^{de} &= T_{l-1}^{de} + W_{l,1} \ast T_{l,1}^{de}+ W_{l,2} \ast T_{l,2}^{de}+W_{l,3} \ast T_{l,3}^{de} \\ \end{align*}\ \ \ \ \ \ \ \ \ 方程四 Sl,1de,Tl,1deSl,2de,Tl,2deSl,3de,Tl,3deTlde=SeriesDecomp (Auto-Correlation(Xl−1de)+Xl−1de)=SeriesDecomp (Auto-Correlation(Sl,1de,XNen)+Sl,1de)=SeriesDecomp (FeedForward(Sl,2de)+Sl,2de)=Tl−1de+Wl,1∗Tl,1de+Wl,2∗Tl,2de+Wl,3∗Tl,3de 方程四
其中, X d e l = S d e l , 3 , l ∈ { 1 , . . . , M } X_{de}^l=S_{de}^{l,3},l\in\{1,...,M\} Xdel=Sdel,3,l∈{1,...,M}表示第 l l l层解码器的输出。 X 0 d e X_0^{de} X0de 是从 X d e s X_{des} Xdes 中嵌入的,用于深度变换,而 T 0 d e = X d e t T_0^{de} = X_{det} T0de=Xdet 用于累积。 S l , i d e S_{l,i}^{de} Sl,ide 和 T l , i d e T_{l,i}^{de} Tl,ide,其中 i ∈ { 1 , 2 , 3 } i ∈ \{1, 2, 3\} i∈{1,2,3},分别表示在第 l l l 层中经过第 i i i 个序列分解块后的季节组分和趋势-周期组分。 W l , i W_{l,i} Wl,i,其中 i ∈ { 1 , 2 , 3 } i ∈ \{1, 2, 3\} i∈{1,2,3},表示第 i i i 个提取的趋势 T l , i d e T_{l,i}^{de} Tl,ide 的投影器。
最终的预测是这两个细化后的分解组分的和,即 W S ∗ X M d e + T M d e W_S * X_M^{de} + T_M^{de} WS∗XMde+TMde,其中 W S W_S WS 是将深度变换后的季节组分 X M d e X_M^{de} XMde 投影到目标维度的投影器。
自相关机制

提出了具有序列间连接的自相关机制,以扩大信息利用率。自相关机制通过计算序列的自相关来发现基于周期的依赖关系,并通过时间延迟聚合来聚合相似的子序列。
基于周期的依赖关系,观察到在周期中的相同相位位置自然提供了相似的子过程。受随机过程理论的启发,对于一个真实的离散时间过程 { X t } \{X_t\} {Xt},我们可以通过以下方程得到自相关 R X X ( τ ) R_{XX}(τ) RXX(τ):
R X X ( τ ) = lim L → ∞ 1 L ∑ t = 1 L X t X t − τ 方程五 R_{XX}(\tau) = \lim_{L \to \infty} \frac{1}{L} \sum_{t=1}^{L} X_t X_{t-\tau}\\ 方程五 RXX(τ)=L→∞limL1t=1∑LXtXt−τ方程五
R X X ( τ ) R_{XX}(τ) RXX(τ)反映了 { X t } \{X_t\} {Xt}与其延迟 τ τ τ的序列 { X t − τ } \{X_{t−τ}\} {Xt−τ}之间的时间延迟相似性。如图所示,我们使用自相关 R ( τ ) R(τ) R(τ)作为估计周期长度τ的非标准化置信度。然后,我们选择最可能的 k k k个周期长度 τ 1 , … , τ k τ_1,…,τ_k τ1,…,τk。基于上述估计的周期,可以推导出基于周期的依赖关系,并可以通过相应的自相关进行加权。
时间延迟聚合 基于周期的依赖关系连接了估计周期内的子序列。因此,我们提出了时间延迟聚合模块,该模块可以根据选定的时间延迟 τ 1 , … , τ k τ_1,…,τ_k τ1,…,τk滚动序列。这种操作可以将处于估计周期相同相位位置的相似子序列对齐,这与自注意力家族中的逐点点积聚合不同。最后,我们通过 s o f t m a x softmax softmax归一化的置信度聚合子序列。对于单头情况和长度为 L L L的时间序列 X X X,经过投影器后,我们得到查询 Q Q Q、键 K K K和值 V V V。因此,它可以无缝地替代自注意力。自相关机制如下:
τ 1 , … , τ k = arg Top k { R Q , K ( τ ) } R ^ Q , K ( τ 1 ) , … , R ^ Q , K ( τ k ) = SoftMax ( R Q , K ( τ 1 ) , … , R Q , K ( τ k ) ) Auto-Correlation ( Q , K , V ) = ∑ i = 1 k Roll ( V , τ i ) ⋅ R ^ Q , K ( τ i ) 方程六 \tau_1, \ldots, \tau_k = \text{arg Top}_k \left\{ R_{Q, K}(\tau) \right\} \\ \widehat{R}_{Q, K}(\tau_1), \ldots, \widehat{R}_{Q, K}(\tau_k) = \text{SoftMax} \left( R_{Q, K}(\tau_1), \ldots, R_{Q, K}(\tau_k) \right) \\ \text{Auto-Correlation}(Q, K, V) = \sum_{i=1}^{k} \text{Roll}(V, \tau_i) \cdot \widehat{R}_{Q, K}(\tau_i)\\方程六 τ1,…,τk=arg Topk{RQ,K(τ)}R Q,K(τ1),…,R Q,K(τk)=SoftMax(RQ,K(τ1),…,RQ,K(τk))Auto-Correlation(Q,K,V)=i=1∑kRoll(V,τi)⋅R Q,K(τi)方程六
其中 a r g T o p k ( ⋅ ) arg\ Topk(⋅) arg Topk(⋅)是获取 T o p k Topk Topk个自相关值的参数,并令$k=\lfloor c×logL \rfloor , , ,c 是一个超参数。 是一个超参数。 是一个超参数。R_{Q,K} 是序列 是序列 是序列Q 和 和 和K 之间的自相关。 之间的自相关。 之间的自相关。Roll(X,τ) 表示对 ∗ X ∗ 进行时间延迟 表示对*X*进行时间延迟 表示对∗X∗进行时间延迟τ 的操作,其中超出第一个位置的元素将被重新引入到最后的位置。对于编码器 − 解码器自相关, 的操作,其中超出第一个位置的元素将被重新引入到最后的位置。对于编码器-解码器自相关, 的操作,其中超出第一个位置的元素将被重新引入到最后的位置。对于编码器−解码器自相关,K 、 、 、V 来自编码器 来自编码器 来自编码器X_{en}^N 并会被调整为长度 并会被调整为长度 并会被调整为长度O ,而 ,而 ,而Q 来自解码器的前一个块。对于 来自解码器的前一个块。对于 来自解码器的前一个块。对于Autoformer 中使用的多头版本,具有 中使用的多头版本,具有 中使用的多头版本,具有d_{model} 个通道和 个通道和 个通道和h 个头的隐藏变量,第 个头的隐藏变量,第 个头的隐藏变量,第i 个头的查询、键和值是 个头的查询、键和值是 个头的查询、键和值是Q_i,K_i,V_i\in \mathbb{R}^{L\times \frac{d_{model}}{h}},i\in{1,…,h}$,。其过程如下:
MultiHead ( Q , K , V ) = W output × Concat ( head 1 , … , head h ) where head i = Auto-Correlation ( Q i , K i , V i ) 方程七 \text{MultiHead}(Q, K, V) = W_{\text{output}} \times \text{Concat}(\text{head}_1, \ldots, \text{head}_h) \\ \text{where } \text{head}_i = \text{Auto-Correlation}(Q_i, K_i, V_i)\\方程七 MultiHead(Q,K,V)=Woutput×Concat(head1,…,headh)where headi=Auto-Correlation(Qi,Ki,Vi)方程七
高效计算:对于基于周期的依赖关系,这些依赖关系指向底层周期中相同相位位置的子过程,并且本质上是稀疏的。在这里,我们选择最可能的延迟来避免选择相反的相位。由于我们聚合了 O ( l o g L ) O(log L) O(logL)个长度为 L L L的序列,因此方程 6 6 6和 7 7 7的复杂度为 O ( L l o g L ) O(Llog L) O(LlogL)。对于自相关计算(方程 5 5 5),给定时间序列 { X t } , R X X ( τ ) \{X_t\},R_{X X} (τ) {Xt},RXX(τ)可以通过基于维纳-辛钦定理的快速傅里叶变换( F F T FFT FFT)来计算:
S X X ( f ) = F ( X t ) F ∗ ( X t ) = ∫ − ∞ ∞ X t e − i 2 π t f d t ⋅ ∫ − ∞ ∞ X t e − i 2 π t f d t ‾ R X X ( τ ) = F − 1 ( S X X ( f ) ) = ∫ − ∞ ∞ S X X ( f ) e i 2 π f τ , d f 方程八 \begin{align*} S_{XX}(f) &=F(X_t) F^*(X_t) = \int_{-\infty}^{\infty} X_t e^{-i2\pi tf} dt \cdot \overline{\int_{-\infty}^{\infty} X_t e^{-i2\pi tf} dt}^ \ \\R_{XX}(\tau) &= F^{-1}(S_{XX}(f)) = \int_{-\infty}^{\infty} S_{XX}(f) e^{i2\pi f\tau} , df \end{align*}方程八 SXX(f)RXX(τ)=F(Xt)F∗(Xt)=∫−∞∞Xte−i2πtfdt⋅∫−∞∞Xte−i2πtfdt =F−1(SXX(f))=∫−∞∞SXX(f)ei2πfτ,df方程八
其中 τ ∈ { 1 , . . . , L } τ ∈ \{1, ..., L\} τ∈{1,...,L}, F F F表示 F F T FFT FFT, F − 1 F^{-1} F−1是其逆变换。 ∗ * ∗表示共轭操作, S X X ( f ) S_{X X} (f) SXX(f)是频域中的。请注意,通过 F F T FFT FFT可以一次性计算 { 1 , . . . , L } \{1, ..., L\} {1,...,L}中所有延迟的序列自相关。因此,自相关计算达到了 O ( L l o g L ) O(Llog L) O(LlogL)的复杂度。
自相关与自注意族
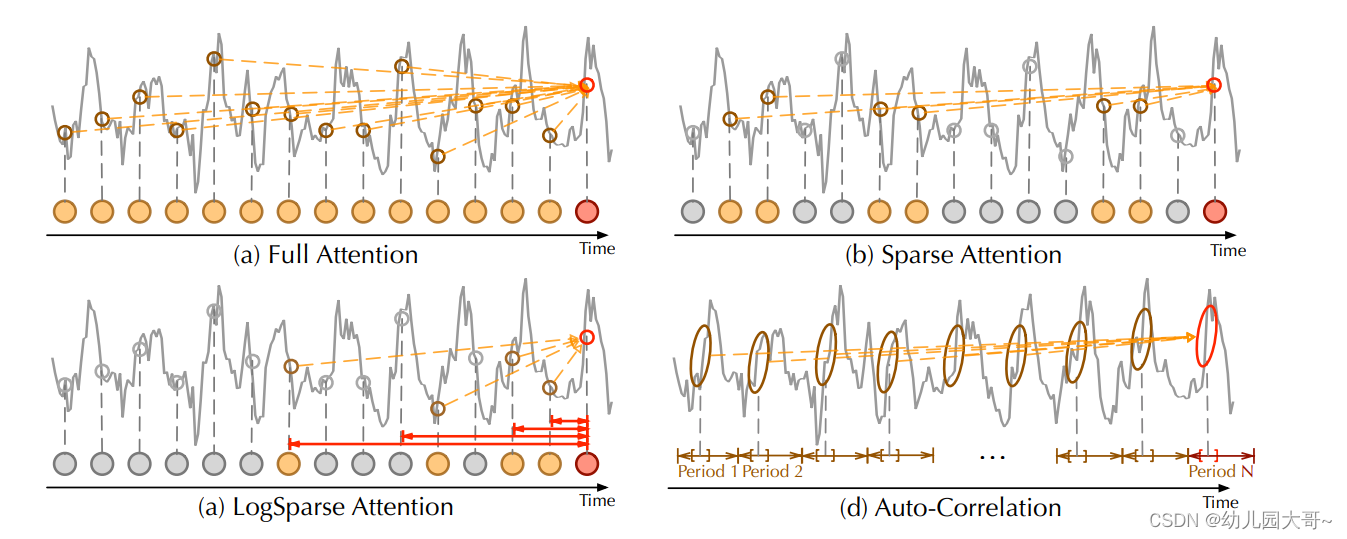
与逐点自注意力族不同,自相关展示了序列之间的连接(如图所示)。具体来说,对于时间依赖性,我们基于周期性来查找子序列之间的依赖关系。相比之下,自注意力族仅计算分散点之间的关系。尽管一些自注意力机制考虑了局部信息,但它们仅利用这些信息来帮助发现逐点依赖关系。对于信息聚合,我们采用时间延迟块来聚合来自底层周期中的相似子序列。相反,自注意力通过点积来聚合选定的点。得益于固有的稀疏性和子序列级别的表示聚合,自相关可以同时提高计算效率和信息利用率。
4.实验
相关文章:

Autoformer
A u t o f o r m e r Autoformer Autoformer 摘要 我们设计了 A u t o f o r m e r Autoformer Autoformer作为一种新型分解架构,带有自相关机制。我们打破了序列分解的预处理惯例,并将其革新为深度模型的基本内部模块。这种设计使 A u t o f o r m…...
uniapp录音播放功能
ui效果如上。 播放就开始倒计时,并且改变播放icon,另外录音则停止上一次录音。 播放按钮(三角形)是播放功能,两竖是暂停播放功能。 const innerAudioContext wx.createInnerAudioContext();export default{data(){ret…...

✊构建浏览器工作原理知识体系(网络协议篇)
🌻 前言 书接上回~ 系列文章目录: # ✊构建浏览器工作原理知识体系(开篇)# ✊构建浏览器工作原理知识体系(浏览器内核篇)# ✊构建浏览器工作原理知识体系(网络协议篇)✊构建浏览器工作原理知识体系(网页加载超详细全过程篇)为什么你觉得偶尔看浏览器的工作原理,…...

【AI大模型】Transformers大模型库(八):大模型微调之LoraConfig
目录 一、引言 二、LoraConfig配置参数 2.1 概述 2.2 LoraConfig参数说明 2.3 代码示例 三、总结 一、引言 这里的Transformers指的是huggingface开发的大模型库,为huggingface上数以万计的预训练大模型提供预测、训练等服务。 🤗 Transformers …...
8-1RT-Thread消息队列
8-1RT-Thread消息队列 消息队列又称队列,是一种常用于线程间通信的数据结构。 消息队列控制块里有两个链表,空闲列表用来挂接空的小几块,另一个链表是用来挂接存有消息的消息框。其中消息链表头指向消息队列当中的第一个消息框,而…...
解除网站IP抓取限制的方法有哪些?
在爬取网站数据时,经常会遇到IP被限制,导致返回的数据无法显示或者直接空白的情况。这时候就需要采取一些方法来解除网站对IP的爬取限制。IP代理是帮助用户绕过网站限制,保持稳定连接,实现数据顺畅爬取的重要解决方案。 1、IP代理…...

“手撕”二叉树的OJ习题
故事的开头,我们先来三道不是oj的开胃菜,练练手感,后面9道都是OJ题。 目录 第一题 第二题 第三题 第四题 第五题 第六题 第七题 第八题 第九题 第十题 第十一题 第一题 二叉树前序非递归遍历实现 。 首先我们需要一个栈来存放二…...

Linux Mint 21.3简介
Linux Mint 21.3是一个更新版本,其中包含了许多新特性和改进。以下是一些主要更新内容: 1. Cinnamon 6.0桌面环境:Linux Mint 21.3采用了最新的Cinnamon 6.0桌面环境,带来了新的功能和改进,例如支持Wayland会话&#…...

C++11 面试题整理
C面试题 1 菱形继承 2 多态 多态实现原理: 静态多态 动态多态 静态多态: 依赖函数重载,编译期确定。 函数重载:允许在同一作用于内声明多个功能类似的同名函数,函数列表不同。注意:不能仅通过返回值类型…...

【智能制造-2】焊缝跟踪
焊缝跟踪? 焊缝跟踪:指在焊接位置前方安装光学传感器进行数据采集,然后传输到焊接机器人,进行自适应的各种模糊控制算法校正焊接机器人或专机的轨迹,实现自适应控制,达到实时的焊缝跟踪。 焊缝跟踪的方法…...

优思学院|用ChatGPT快速完成数据分析图表【柏累托图法】
数据分析是很多行业的人不可少的一部分,尤其是质量工程师更是日常的工作。然而,随着科技的进步,人工智能(AI)将逐渐承担起数据计算的工作,这意味着未来的质量工程师需要具备的不仅仅是计算能力,…...

[晕事]今天做了件晕事37 extern “C“ 被认为了是外部函数
最近看到一个函数声明是 extern “C" void _dump(); 这里的声明是要告诉编译器,这个_dump是C语言的符号,没有经过mangle过的。但是这个关键字可能让人混淆是外部函数。因为这个关键字可以声明外部函数。这也算是一词多用的一个普遍问题。关键的关键…...
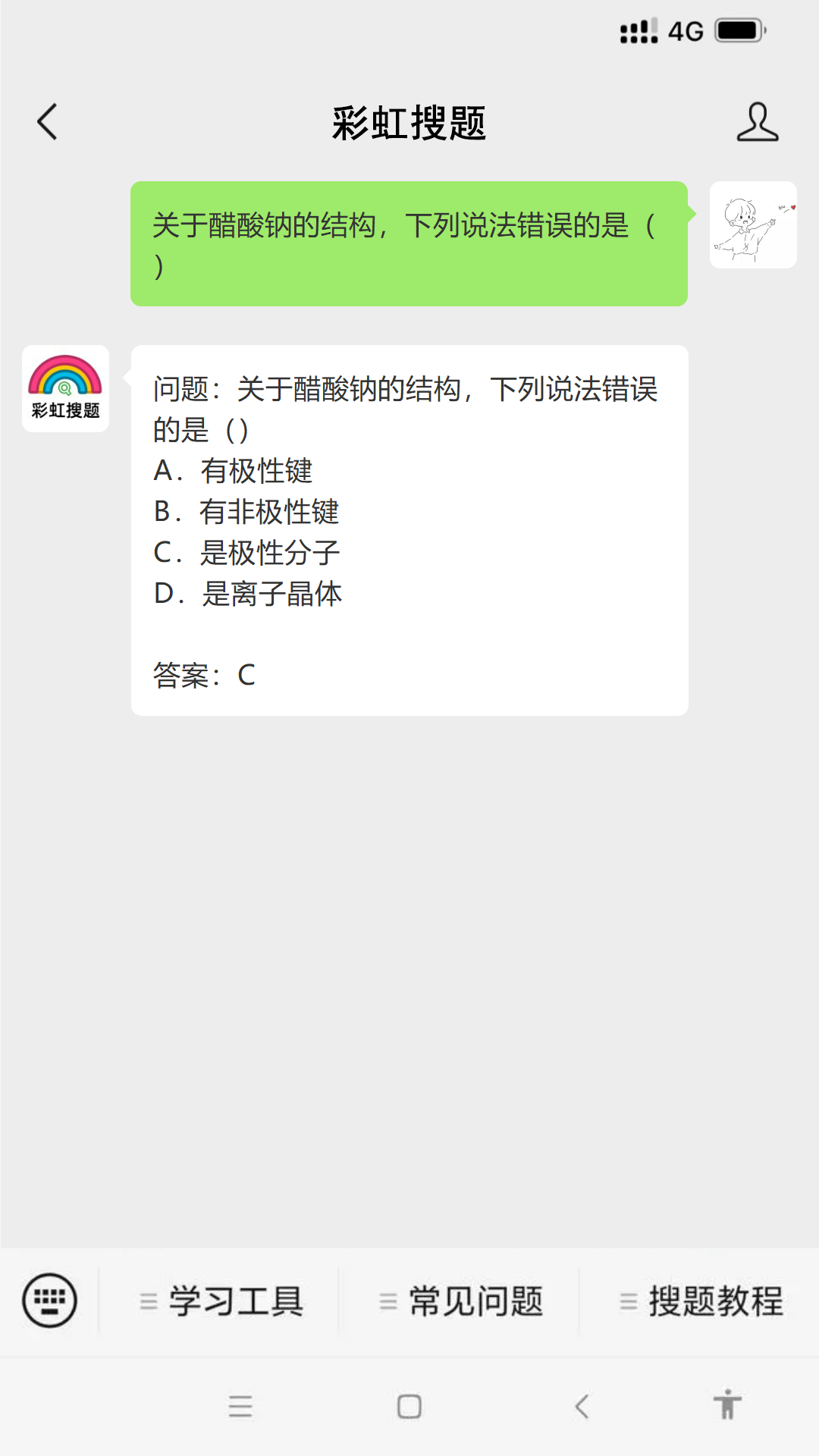
问题:关于醋酸钠的结构,下列说法错误的是() #媒体#媒体
问题:关于醋酸钠的结构,下列说法错误的是() A.有极性键 B.有非极性键 C.是极性分子 D.是离子晶体 参考答案如图所示...
)
网络安全(补充)
同步包风暴(SYN Flood)攻击者假造源网址发送多个同步数据包(SYN Packet)给服务器,服务器因无法收到确认数据包(ACK Packet),使TCP/IP协议三次握手无法顺利完成,因而无法建…...
)
Redis集群(3)
集群扩容 节点配置和启动 我们要加入两个节点,主节点端口为6903,从节点端口为6933。配置与6900节点类似,不再赘述。启动这两个节点: ./redis-server ../conf/cluster_m_6903.conf ./redis-server ../conf/cluster_s_6933.conf加…...
防止Selenium被检测 Google Chrome 125
背景 最近在使用selenium自动播放学习课程,相信大家也有一些类似的使用场景。 能自动化的事情,绝不自己干。 为防止被检测是机器人做题,刷视频,需要做一些小调整。 先来看作为服务方维护者,是如何检测是Selenium打…...
LeetCode 算法:螺旋矩阵c++
原题链接🔗:螺旋矩阵 难度:中等⭐️⭐️ 题目 给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]] 输出&…...
【全开源】医护上门系统小程序APP公众号h5源码
医护上门系统:健康守护,就在您身边 🚪引言:开启全新的医护模式 在快节奏的现代生活中,健康问题往往成为我们关注的焦点。而“医护上门系统”正是为了满足这一需求,将专业的医疗服务送到您的家中。这一创新…...

结构体<C语言>
导言 结构体是C语言中的一种自定义类型,它的值(成员变量)可以是多个,且这些值可以为不同类型,这也是和数组的主要区别,下面将介绍它的一些基本用法,包括:结构体的创建、结构体变量的…...

点云分割报告整理(未完成版-每天写一点)
体积占用网格表示对点进行体素化,然后使用3d卷积神经网络来学习体素级语义。由于点云的稀疏性,体素化效率低,为避免较高的计算成本而忽略了细节。此外,由于同一体素内的所有点都被赋予了相同的语义标签,因此精度受到限…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...
