探究Vue源码:深入理解diff算法
前言
在Vue中 组件初次渲染时,会调用 render 函数生成初始的虚拟 DOM 树。
当组件的状态发生变化时,Vue 会重新调用 render 函数生成新的虚拟 DOM 树。
而Diff 算法是用来比较新旧虚拟 DOM 树的差异,并且只对差异部分进行更新的算法,从而尽量减少性能开销。
虚拟DOM树是什么?
描述组件视图结构的虚拟节点树,也就是VNode树
,它描述了一个 DOM 节点的信息,包括节点类型、属性、子节点等。
实现vNode
function createVNode(type?,props?,children?){const vnode = {type,props,children,}return vnode
}
运用虚拟 DOM 可以将真实 DOM 的操作转换为JS对象的操作,避免了频繁的直接操作真实 DOM 带来的性能损耗。我们可以运用虚拟DOM的属性来进行操作,vnode 的 children 数组中对应子节点的 vnode 对象,所以在 vue 中通过 vnode 和真实的 DOM 树进行映射,我们也称之为虚拟树。
实现Diff算法
锁定需要改变的位置 处理前置和后置没有改变的元素
预处理前置节点
定义一个头指针
function patchkeyChildren(c1,c2){let i = 0;//c1为旧let e1 = c1.length - 1;let e2 = c2.length - 1;function isSomeVNodeType(n1, n2) {return n1.type === n2.type && n1.key JJJ=== n2.key
}while (i <= e1 && i <= e2) {const n1 = c1[i]const n2 = c2[i]if (isSomeVNodeType(n1, n2)) {patch(n1, n2,...)} else {break;}i++;}
}
预处理后置节点
function patchkeyChildren(c1,c2,...){
...
...
while(i <= e1 && i <= e2) {const n1 = c1[e1]const n2 = c2[e2]if (isSomeVNodeType(n1, n2)) {
patch(n1, n2,... )
} else {
break;
}
e1--;e2--;}
}
3.处理仅有新增节点情况 新节点比老节点多
function patchkeyChildren(c1,c2,...){
...
...
if (i > e1) {
if (i <= e2) {
while (i <= e2) {
patch(null, c2[i],...)
i++;
}
}
}
4.处理仅有卸载节点情况也就是老节点比新节点多
老节点 a b c
新节点 a b
function patchkeyChildren(c1,c2,...){
...
...
if(i > e2){if(i <= e1){while(i <= e1){unmount(c1[i].el)}}
}
}
⭐️⭐️⭐️5.处理其他情况(新增/卸载/移动)
创建新的 在老的里面不存在,在新的里面存在
删除老的 在老的里面存在,新的里面不存在
移动 节点存在于新的和老的节点,但是位置变了
实现删除功能
两种方法查找新节点到底存在于老节点 一种方法是遍历 ,另一种是Key,Key是节点的唯一标识 能提高效率 这也是Vue中为何总要写key属性
定义s1、s2变量 分别记录要处理部分的起始位置
...
else{
let s1 = i;//旧节点开始位置
let s2 = i;//新节点开始位置const keyToNewIndexMap = new Map()
//遍历新节点保存key映射表
for (let i = s2; i <= e2; i++) {const nextChild = c2[i]keyToNewIndexMap.set(nextChild.key, i)}
}
for(let i = s1; i <= e1; i++){const prevChild = c1[i]let newindex;if (prevChild.key != null) {newIndex = keyToNewIndexMap.get(prevChild.key)} else {for (let j = s2; j <= e2; j++) {if (isSomeVNodeType(prevChild, c2[j])) {newIndex = j;break;}}
}
//如果没有找到 则直接删除旧节点中元素
if (newIndex === undefined) {unMount(prevChild.el)}else{patch(prevChild, c2[newIndex], ...)
}
}优化 中间部分老的比新的多 那么多出来的可以直接删掉
const toBePatched = e2 - s2 + 1;
let patched = 0;for (let i = s1; i <= e1; i++) {
...
if (patched >= toBePatched) {unMount(prevChild.el)continue;}//在patch后
...
patched++
移动实现
这里就需要借助最长递增子序列算法提高效率了 因为要移动位置 要频繁dom操作,效率很慢,可以筛选那些老节点和新节点都有递增有顺序的节点不动
//先建立映射关系
const newIndexToOldIndexMap = new Array(toBePatched)
for (let i = 0; i < toBePatched; i++) newIndexToOldIndexMap[i] = 0
...
...
//在patch前实现
newIndexToOldIndexMap[newIndex - s2] = i + 1; //不能把值设为0 他是有特殊意义的patch(prevChild, c2[newIndex], container, ...)const increasingNewIndexSequence =getSequence(newIndexToOldIndexMap)
//指针
let j = 0
for(let i =0;i < toBePatched; i++){if(i !==increasingNewIndexSequence[j]){console.log("移动位置")}else{j++}
}
优化 调用最长递增子序列也会浪费一定性能 当 可以定义一个变量moved 如果移动再开始
没有移动则为false
let moved = false;
let maxNewIndexSoFar = 0;
...
if (newIndex >= maxNewIndexSoFar) {maxNewIndexSoFar = newIndex} else {moved = true}
...
const increasingNewIndexSequence = moved ? getSequence(newIndexToOldIndexMap) : []
if(moved){console.log('插入操作')
}
创建新的节点
if (newIndexToOldIndexMap[i] === 0) {
patch(null, nextChild)
}
实现完成. 完整代码
function patchKeyedChildren(c1: any, c2: any, container, parentComponent, parentAnchor) {let i = 0let e1 = c1.length - 1;let e2 = c2.length - 1function isSomeVNodeType(n1, n2) {return n1.type === n2.type && n1.key === n2.key}// 左侧while (i <= e1 && i <= e2) {const n1 = c1[i]const n2 = c2[i]if (isSomeVNodeType(n1, n2)) {patch(n1, n2, container, parentComponent, parentAnchor)} else {break;}i++;}while (i <= e1 && i <= e2) {const n1 = c1[e1]const n2 = c2[e2]if (isSomeVNodeType(n1, n2)) {patch(n1, n2, container, parentComponent, parentAnchor)} else {break;}e1--;e2--;}if (i > e1) {if (i <= e2) {const nextPos = e2 + 1;const anchor = e2 + 1 < c2.length ? c2[nextPos].el : nullwhile (i <= e2) {patch(null, c2[i], container, parentComponent, anchor)i++;}}} else if (i > e2) {while (i <= e1) {
//删除操作
hostRemove(c1[i].el)i++}} else { // Array to Array 中间乱序let s1 = i;let s2 = i;const keyToNewIndexMap = new Map()for (let i = s2; i <= e2; i++) {const nextChild = c2[i]keyToNewIndexMap.set(nextChild.key, i)}const toBePatched = e2 - s2 + 1;let patched = 0;const newIndexToOldIndexMap = new Array(toBePatched)// 中间值发生改变再调用方法let moved = false;let maxNewIndexSoFar = 0for (let i = 0; i < toBePatched; i++) newIndexToOldIndexMap[i] = 0for (let i = s1; i <= e1; i++) {const prevChild = c1[i];if (patched >= toBePatched) {hostRemove(prevChild.el)continue;}let newIndex;if (prevChild.key != null) {newIndex = keyToNewIndexMap.get(prevChild.key)} else {for (let j = s2; j <= e2; j++) {if (isSomeVNodeType(prevChild, c2[j])) {newIndex = j;break;}}}if (newIndex === undefined) {hostRemove(prevChild.el)} else {if (newIndex >= maxNewIndexSoFar) {maxNewIndexSoFar = newIndex} else {moved = true}// 能代表新节点存在newIndexToOldIndexMap[newIndex - s2] = i + 1; //不能把值设为0 他是有特殊意义的patch(prevChild, c2[newIndex], container, parentComponent, null)patched++;}}const increasingNewIndexSequence = moved ? getSequence(newIndexToOldIndexMap) : []let j = increasingNewIndexSequence.length - 1;for (let i = toBePatched - 1; i >= 0; i--) {const nextIndex = i + s2;const nextChild = c2[nextIndex]const anchor = nextIndex + 1 < c2.length ? c2[nextIndex + 1].el : null;if (newIndexToOldIndexMap[i] === 0) {patch(null, nextChild, container, parentComponent, anchor)}if (moved) {if (j < 0 || i !== increasingNewIndexSequence[j]) {hostinsert(nextChild.el, container, anchor)} else {j--}}}}}
//递增子序列算法
function getSequence(arr: number[]): number[] {const p = arr.slice();const result = [0];let i, j, u, v, c;const len = arr.length;for (i = 0; i < len; i++) {const arrI = arr[i];if (arrI !== 0) {j = result[result.length - 1];if (arr[j] < arrI) {p[i] = j;result.push(i);continue;}u = 0;v = result.length - 1;while (u < v) {c = (u + v) >> 1;if (arr[result[c]] < arrI) {u = c + 1;} else {v = c;}}if (arrI < arr[result[u]]) {if (u > 0) {p[i] = result[u - 1];}result[u] = i;}}}u = result.length;v = result[u - 1];while (u-- > 0) {result[u] = v;v = p[v];}return result;}
相关文章:

探究Vue源码:深入理解diff算法
前言 在Vue中 组件初次渲染时,会调用 render 函数生成初始的虚拟 DOM 树。 当组件的状态发生变化时,Vue 会重新调用 render 函数生成新的虚拟 DOM 树。 而Diff 算法是用来比较新旧虚拟 DOM 树的差异,并且只对差异部分进行更新的算法,从而尽量…...

qt自适应图片
在 Qt 中,通过重写 paintEvent 方法来添加自适应背景图片的过程如下: 创建一个自定义的 QWidget 子类。重写 paintEvent 方法,在该方法中使用 QPainter 绘制背景图片。使用 QPixmap 加载图片,并调整图片的大小以适应窗口的大小。…...

【区块链】解码拜占庭将军问题:区块链共识机制的哲学基石
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 解码拜占庭将军问题:区块链共识机制的哲学基石引言一、拜占庭将军问…...

MCK主机加固:智能科技,构筑网络安全的铜墙铁壁
在数字化转型的浪潮中,企业服务器的安全已成为维护业务连续性和保护数据资产的关键。MCK主机加固产品,以其创新技术,为企业提供了一个全面、智能、高效的安全解决方案。 一、智能安全监测 MCK主机加固产品采用深度学习算法,能够…...
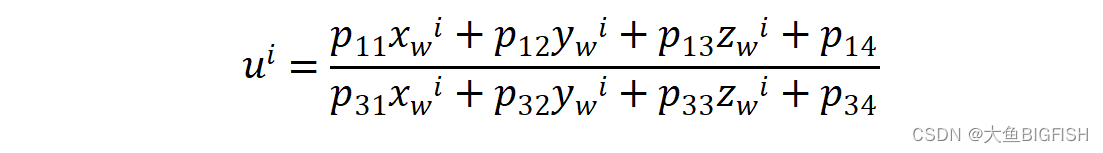
OpenCV 双目相机标定
文章目录 一、简介1.1单目相机标定1.2双目相机标定二、实现代码三、实现效果参考资料一、简介 1.1单目相机标定 与单目相机标定类似,双目标定的目的也是要找到从世界坐标转换为图像坐标所用到的投影P矩阵各个系数(即相机的内参与外参)。具体过程如下所述: 1、首先我们需要…...
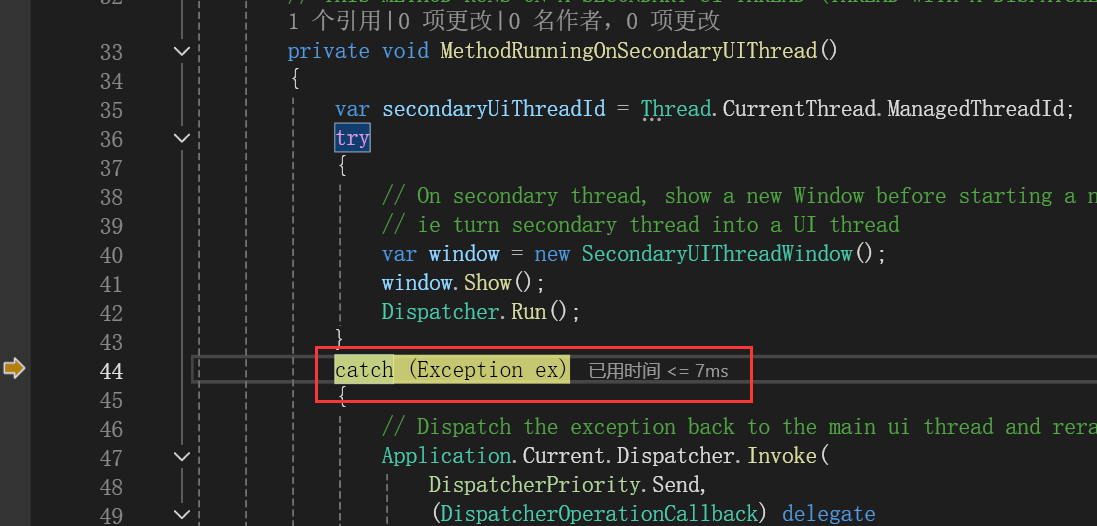
WPF/C#:异常处理
什么是异常? 在C#中,异常是在程序执行过程中发生的特殊情况,例如尝试除以零、访问不存在的文件、网络连接中断等。这些情况会中断程序的正常流程。 当C#程序中发生这种特殊情况时,会创建一个异常对象并将其抛出。这个异常对象包…...
2024年跨平台应用解决方法
个人博客:Sekyoro的博客小屋 个人网站:Proanimer的个人网站 很久没有写这类high-level的文章了,本身这类框架就一直层出不穷,但是其中历久弥坚,坚韧不拔的框架又有多少呢? 首先考虑到学习成本以及掌握一些编程语言在工作、学习生态上的价值,给这些东西适用生态划分一下. Reac…...
人工智能ChatGPT的多种应用:提示词工程
简介 ChatGPT 的主要优点之一是它能够理解和响应自然语言输入。在日常生活中,沟通本来就是很重要的一门课程,沟通的过程中表达的越清晰,给到的信息越多,那么沟通就越顺畅。 和 ChatGPT 沟通也是同样的道理,如果想要 …...

OceanBase v4.2 解读:tenant=all 语义优化,提升易用性
1 背景 1.1 租户类型及特点 OceanBase中有三种类型的租户: sys租户:集群默认创建,生命周期与集群相一致,管理集群和其他租户,具有较高的地位。用户租户:用户创建的业务租户或普通租户,用于运…...

理论和实验
一、理论和实验的关系 (一)理论可以指导实验 理论家提出理论和猜想,实验家就可以做个实验来验证是否适用。 (二)实验可以提升理论认识 实验家通过做实验,观察实验过程和结果后,如果发现和理论预测有误差,那么理论家就能根据新发现…...

Linux 常用命令 - userdel 【删除用户】
简介 userdel 这个命令源自于 “user delete”,即用户删除。这个命令主要用于在 Linux 系统中删除用户账户及其相关文件。当管理员需要移除一个用户及其在系统中的所有踪迹时,会用到这个命令。 使用方式 userdel [选项] 用户名常用参数 -f:强制删除用户,即使用户当前已登…...

等保测评和安全运维
# 等保测评与安全运维:构建企业网络安全的双重保障 引言 在数字化时代,企业面临着日益复杂的网络安全威胁。为了应对这些挑战,企业不仅要实施有效的安全运维措施,还需要通过等保测评确保其信息系统符合国家的安全标准。本文将探讨…...
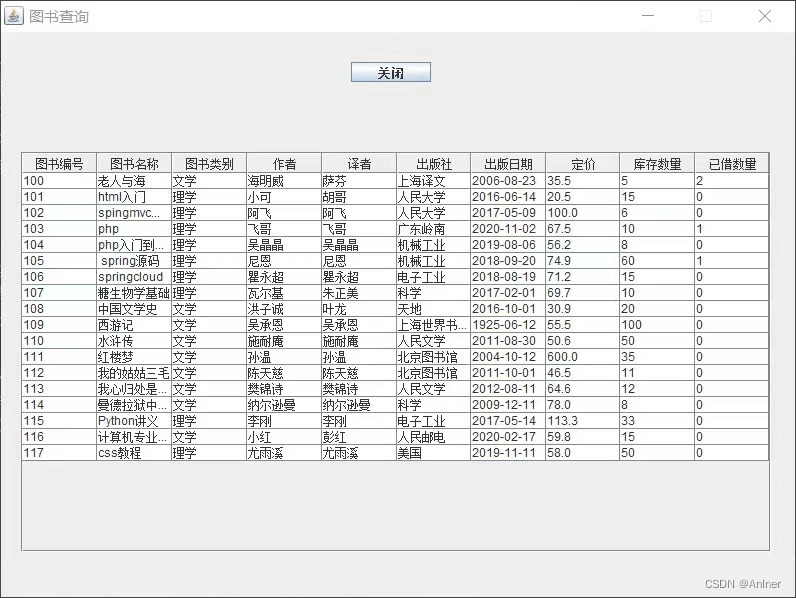
Java课程设计:基于Java+Swing+MySQL的图书管理系统(内附源码)
文章目录 一、项目介绍二、项目展示三、源码展示四、源码获取 一、项目介绍 图书管理系统是一个常见的软件项目,广泛应用于图书馆、学校、企业等需要管理图书资源的场景。该系统通常涵盖图书信息录入、查询、借阅、归还等核心功能,是实现图书资源高效管理的重要工具。 随着信…...

WireGuard网络架构及配置详解
WireGuard网络架构及配置详解 一.点对点二.中心网关,实现nat穿透弊端:流量全部经过中心网关,带宽上限受限于中心网关 三.借助registry实现双向nat穿透需要借助registry实现 udp打洞, 待二开 一.点对点 yum install epel-release elrepo-release -y yum install yum-plugin-elr…...
VB.NET实现上位机自动识别可用串口
在实际应用中有时会牵扯到挑选可用串口,比如上位机和从站设备使用Modbus RTU协议进行通讯时需要选择COM串口,每次启动连接前都在设备管理器查看较为麻烦,可以设置一个串口自动识别功能,如果选择了错误的串口还可以提示串口选择错误…...
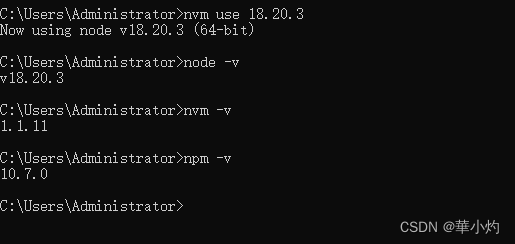
Node.js版本管理工具-NVM
在开发 Node.js 项目时,经常会遇到需要切换不同版本的 Node.js 的情况。为了方便管理和切换各个版本,我们可以使用一些 Node.js 版本管理工具。 Node Version Manager:简称NVM,最流行的 Node.js 版本管理工具之一。它允许我们在同…...

【react】useEffect 快速上手
useEffect 快速上手 useEffect(setup, dependencies?) 可以接收两个参数,分别是回调函数与依赖数组. useEffect 用什么姿势来调用,本质上取决于你想用它来达成什么样的效果。下面我们来简单介绍 useEffect 的调用规则。 每一次渲染后都执行的副作用&a…...

docker容器部署jenkins
提前安装好jdk和maven,jdk最好使用11版本,jdk-11.0.10 docker run -u root -d \ -p 100:8080 \ -v /var/jenkins_home/workspace/:/var/jenkins_home/workspace/ \ -v /var/run/docker.sock:/var/run/docker.sock \ -v /usr/bin/docker:/usr/bin/docker…...

第十四章 享元模式
目录 1 享元模式介绍 2 享元模式原理 3 享元模式实现 4 享元模式应用实例 5 享元模式总结 1 享元模式介绍 享元模式 (flyweight pattern) 的原始定义是:摒弃了在每个对象中保存所有数据的方式,通过共享多个对象所共有的相同状态,从而让我…...
ThinkBook 16 2024 Ubuntu 触控板问题解决
sudo insmod goodix-gt7868q.ko sudo cp local-overrides.quirks /etc/libinput/local-overrides.quirks sudo systemctl restart gdm 有偿解决,无效退款...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
