37、matlab矩阵运算
1、前言
矩阵运算是指对矩阵的各种操作和运算,包括矩阵加法、矩阵减法、矩阵乘法、矩阵转置、求逆矩阵等。以下是常见的矩阵运算:
-
矩阵加法:对应位置的元素相加,要求加数和被加数的维度相同。
A + B = | a11 b11 | + | a12 b12 | | a21 b21 | | a22 b22 |
-
矩阵减法:对应位置的元素相减,要求减数和被减数的维度相同。
A - B = | a11 b11 | - | a12 b12 | | a21 b21 | | a22 b22 |
-
矩阵乘法:按照行乘列的方式计算,要求左矩阵的列数等于右矩阵的行数。
AB = A的行 * B的列
-
矩阵转置:将矩阵的行与列进行交换,即将A的第i行第j列元素变为转置矩阵A^T的第j行第i列元素。
对于矩阵A,A^T表示其转置矩阵。
-
矩阵求逆:对于方阵,如果其行列式不为0,则可以求其逆矩阵A^-1。
如果A是一个可逆矩阵,那么AA^-1 = A^-1A = I,其中I是单位矩阵。
矩阵运算在线性代数、数值分析、工程计算等领域有广泛的应用。例如,在解线性方程组、特征值问题、最小二乘拟合、图像处理等方面都需要用到矩阵运算。熟练掌握矩阵运算的规则和性质对于理解和应用数学模型非常重要。
2、transpose, .' 转置向量或矩阵
语法
B = A.' 返回 A 的非共轭转置,即每个元素的行和列索引都会互换。
B = transpose(A) 是执行 A.' 的另一种方式,它可以为类启用运算符重载。
1)实矩阵转置
代码及运算
A = magic(5)
B = A.'A =17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9B =17 23 4 10 1124 5 6 12 181 7 13 19 258 14 20 21 215 16 22 3 92)复矩阵转置
代码及运算
A = [1 3 4-1i 2+2i; 0+1i 1-1i 5 6-1i]
B = A.'A =1.0000 + 0.0000i 3.0000 + 0.0000i 4.0000 - 1.0000i 2.0000 + 2.0000i0.0000 + 1.0000i 1.0000 - 1.0000i 5.0000 + 0.0000i 6.0000 - 1.0000iB =1.0000 + 0.0000i 0.0000 + 1.0000i3.0000 + 0.0000i 1.0000 - 1.0000i4.0000 - 1.0000i 5.0000 + 0.0000i2.0000 + 2.0000i 6.0000 - 1.0000i3、 ctranspose, ' 复共轭转置
语法
B = A' 计算 A 的复共轭转置。
B = ctranspose(A) 是执行 A' 的替代方法
1)实矩阵的共轭转置
代码及运算
A = [2 1; 9 7; 2 8; 3 5]
B = A'A =2 19 72 83 5B =2 9 2 31 7 8 52) 复矩阵的共轭转置
代码及运算
A = [0-1i 2+1i;4+2i 0-2i]
B = A'A =0.0000 - 1.0000i 2.0000 + 1.0000i4.0000 + 2.0000i 0.0000 - 2.0000iB =0.0000 + 1.0000i 4.0000 - 2.0000i2.0000 - 1.0000i 0.0000 + 2.0000i4、 mtimes, * 矩阵乘法
语法
C = A*B 是 A 和 B 的矩阵乘积。
C = mtimes(A,B) 是执行 A*B 这一操作的替代方法
1)将两个向量相乘
代码及运算
A = [1 1 0 0];
B = [1; 2; 3; 4];
C1 = A*B
C2 = B*AC1 =3C2 =1 1 0 02 2 0 03 3 0 04 4 0 02)将两个数组相乘
代码及运算
A = [1 3 5; 2 4 7];
B = [-5 8 11; 3 9 21; 4 0 8];
C = A*BC =24 35 11430 52 1625、 mpower, ^ 矩阵幂
语法
C = A^B 计算 A 的 B 次幂并将结果返回给 C。
C = mpower(A,B) 是执行 A^B 的替代方法,但很少使用。
1)方阵幂运算
代码及运算
A = [1 2; 3 4];
C = A^2C =7 1015 222)矩阵指数
代码及运算
B = [0 1; 1 0];
C = 2^BC =1.2500 0.75000.7500 1.25006、 sqrtm 矩阵平方根
语法
X = sqrtm(A) 返回矩阵 A 的主要平方根(即 X*X = A)。
[X,residual] = sqrtm(A) 还会返回残差 residual = norm(A-X^2,1)/norm(A,1)
[X,alpha,condx] = sqrtm(A) 以 1-范数形式返回稳定因子 alpha 和 X 的矩阵平方根条件数的估计值,即 condx。
1)差分算子的矩阵平方根
代码及运算
A = [5 -4 1 0 0; -4 6 -4 1 0; 1 -4 6 -4 1; 0 1 -4 6 -4; 0 0 1 -4 6]
X = sqrtm(A)A =5 -4 1 0 0-4 6 -4 1 01 -4 6 -4 10 1 -4 6 -40 0 1 -4 6X =2.0015 -0.9971 0.0042 0.0046 0.0032-0.9971 2.0062 -0.9904 0.0118 0.00940.0042 -0.9904 2.0171 -0.9746 0.02630.0046 0.0118 -0.9746 2.0503 -0.92000.0032 0.0094 0.0263 -0.9200 2.27002)具有多个平方根的矩阵
代码及运算
A = [7 10; 15 22];
Y1 = [1.5667 1.7408; 2.6112 4.1779];
A - Y1*Y1
Y2 = [1 2; 3 4];
A - Y2*Y2
Y = sqrtm(A)ans =1.0e-03 *-0.1258 -0.1997-0.2995 -0.4254ans =0 00 0Y =1.5667 1.74082.6112 4.1779
7、expm 矩阵指数
语法
Y = expm(X) 计算 X 的矩阵指数。
1)指数运算
代码及运算
A = [1 1 0; 0 0 2; 0 0 -1];
expm(A)ans =2.7183 1.7183 1.08620 1.0000 1.26420 0 0.36798、 logm 矩阵对数
语法
L = logm(A) 是 A 的主矩阵对数,即 expm(A) 的倒数。
1)矩阵对数
代码及运算
A = [1 1 0; 0 0 2; 0 0 -1];
P = logm(Y)P =-0.3504 0.92941.3940 1.04369、cross 叉积
语法
C = cross(A,B) 返回 A 和 B 的叉积。
C = cross(A,B,dim) 计算数组 A 和 B 沿维度 dim 的叉积。
1)向量的叉积
代码及运算
A = [4 -2 1];
B = [1 -1 3];
C = cross(A,B)C =-5 -11 -22)矩阵的叉积
代码及运算
A = randi(15,3,5)
B = randi(25,3,5)
C = cross(A,B)A =13 15 6 3 1011 1 12 8 115 7 12 7 12B =7 5 24 6 1317 3 9 19 1817 13 15 7 23C =102 -8 72 -77 37-186 -160 198 21 -74144 40 -234 9 3710、 dot 点积
语法
C = dot(A,B) 返回 A 和 B 的标量点积。
C = dot(A,B,dim) 计算 A 和 B 沿维度 dim 的点积。
1)实数向量的点积
代码及运算
A = [4 -1 2];
B = [2 -2 -1];
C = dot(A,B)C =82)复数向量的点积
代码及运算
A = [1+i 1-i -1+i -1-i];
B = [3-4i 6-2i 1+2i 4+3i];
C = dot(A,B)
D = dot(A,A)C =1.0000 - 5.0000iD =83)矩阵的点积
代码及运算
A = [1 2 3;4 5 6;7 8 9];
B = [9 8 7;6 5 4;3 2 1];
C = dot(A,B)C =54 57 544)多维数组的点积
代码及运算
A = cat(3,[1 1;1 1],[2 3;4 5],[6 7;8 9])
B= cat(3,[2 2;2 2],[10 11;12 13],[14 15; 16 17])
C = dot(A,B,3)A(:,:,1) =1 11 1A(:,:,2) =2 34 5A(:,:,3) =6 78 9B(:,:,1) =2 22 2B(:,:,2) =10 1112 13B(:,:,3) =14 1516 17C =106 140178 220
相关文章:

37、matlab矩阵运算
1、前言 矩阵运算是指对矩阵的各种操作和运算,包括矩阵加法、矩阵减法、矩阵乘法、矩阵转置、求逆矩阵等。以下是常见的矩阵运算: 矩阵加法:对应位置的元素相加,要求加数和被加数的维度相同。 A B | a11 b11 | | a12 b12 | | …...

用软件实现的硬件——虚拟机
通过软件实现CPU和内存等硬件所具有的功能,并在计算机中运行循环的计算机技术称为虚拟机。使用虚拟机,就可以在一台计算机中运行多个循环出来的计算机。 近几年的计算机,除了硬件具有较高的性能外,CPU的性能也有了提升。因此&…...
[Shell编程学习路线]--shell中重定向和管道符(详细介绍)
🏡作者主页:点击! 🛠️Shell编程专栏:点击! ⏰️创作时间:2024年6月12日10点50分 🀄️文章质量:93分 ——前言—— 在Shell编程中,重定向和管道符是两个…...

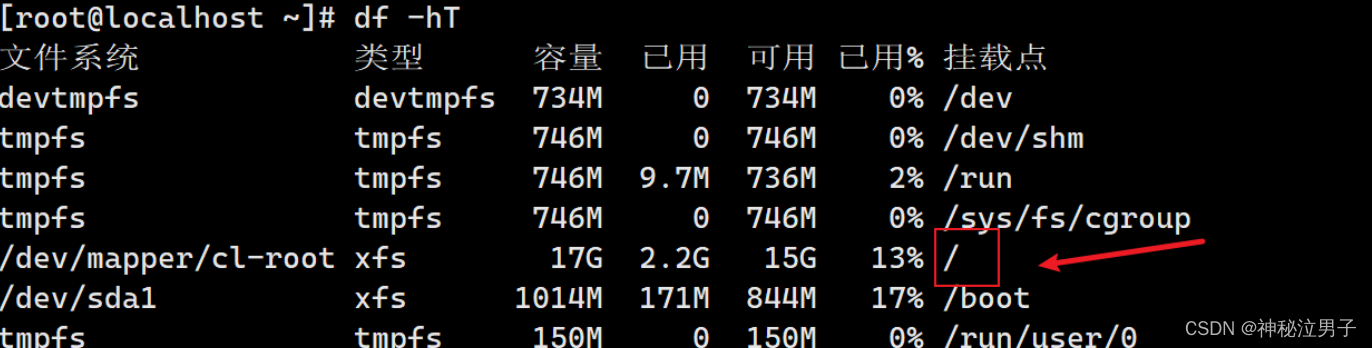
Linux命令详解(1)
在Linux操作系统中,命令行界面(CLI)是一个强大的工具,它允许用户通过键入命令来与系统交互。无论是系统管理员还是普通用户,掌握一些基本的Linux命令都是非常重要的。在本文中,我们将探讨一些常用的Linux命…...

网工内推 | 深信服、中软国际技术支持工程师,最高13k*13薪
01 深信服 🔷招聘岗位:远程技术支持工程师 🔷任职要求: 一、专业能力和行业经验: ①具备友商同岗位工作经验1.5年以上,具备良好的分析和判断能力,有独立问题处理思路,具备常见协…...

实现卡片的展开缩放动画
原理,外层包裹一个元素,子元素分别是展开和收起的元素,然后对展开的元素添加动画,动画内容是随时间变化,将卡片的transform:rotateX属性进行调整,因为改变的是子元素的旋转,父元素高…...

实验:贪心算法
实验二:贪心算法 【实验目的】 应用贪心算法求解活动安排问题。 【实验性质】 验证性实验。 【实验要求】 活动安排问题是可以用贪心算法有效求解的很好的例子。 问题:有n个活动的集合A{1,2,…,n},其中每个活动都要求使用同一资源&…...

Python学习笔记12 -- 有关布尔值的详细说明
一、布尔表达式 最终值为true 或者false 二、常见形式: 1、常量:true false 2、比较运算: and ! 3、复合运算: and and or 4、其他 例:检测闰年: def specialYearMine(year):if (year%4 …...

SQL-窗口函数合集
目录 1.窗口函数简介2.窗口的定义3.相关题目示例3.1 PERCENT_RANK()2346 以百分比计算排名 3.2 FIRST_VALUE()/LAST_VALUE()/NTH_VALUE()2388 将表中的空值更改为前一个值 1.窗口函数简介 MySQL 开窗函数(Window Functions)是 MySQL 8.0 版本引入的一个…...

2024 全球软件研发技术大会官宣,50+专家共话软件智能新范式!
2024年的全球软件研发技术大会(SDCon)由CSDN和高端IT咨询与教育平台Boolan联合主办,将于7月4日至5日在北京威斯汀酒店举行。本次大会的主题为“大模型驱动软件智能化新范式”,旨在探讨大模型和开源技术的发展如何引领全球软件研发…...
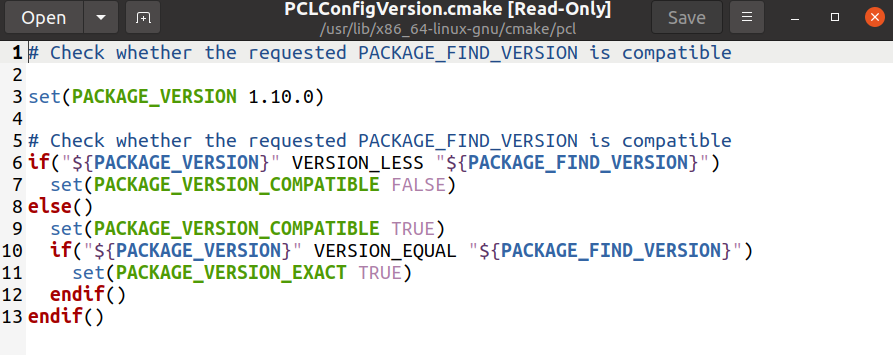
opencv快速安装以及各种查看版本命令
安装opencv并查看其版本,直接通过一个可执行文件实现。 #!/bin/bashwget https://codeload.github.com/opencv/opencv/zip/3.4 -O opencv-3.4.zip && unzip opencv-3.4.zip && cd opencv-3.4 && \mkdir build && cd build &&a…...
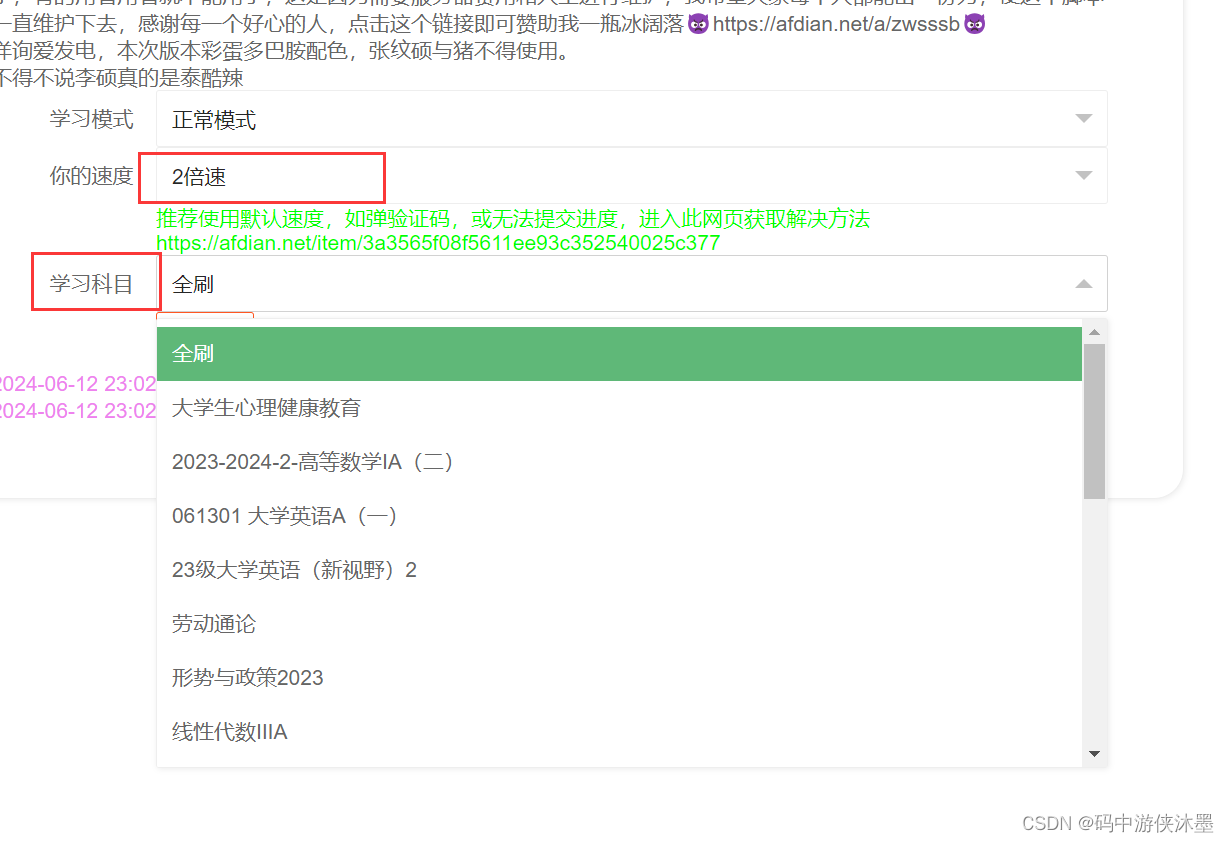
免费学习通刷课(免费高分)Pro版
文章目录 概要整体架构流程小结 概要 关于上一版的免费高分的学习通刷课,有很多人觉得还得登录太复杂了,然后我又发现了个神脚本,操作简单,可以后台挂着,但是还是建议调整速度到2倍速,然后找到你该刷的课&…...

线性数据结构-队列
队列(Queue)是一种先进先出(First In First Out, FIFO)的数据结构,它按照元素进入的顺序来处理元素。队列的基本操作包括: enqueue:在队列的末尾添加一个元素。dequeue:移除队列的第…...

python脚本将视频抽帧为图像数据集
AI应用开发相关目录 本专栏包括AI应用开发相关内容分享,包括不限于AI算法部署实施细节、AI应用后端分析服务相关概念及开发技巧、AI应用后端应用服务相关概念及开发技巧、AI应用前端实现路径及开发技巧 适用于具备一定算法及Python使用基础的人群 AI应用开发流程概…...

Xmind导入纯文本TXT方法
最近有很多同事咨询我如何在xmind直接导入纯文本txt笔记或者思维导图呢? 解决办法如下: 1.先打开xmind随便打开一个思维导图-文件-导出-marldown 2.选中导出的markdown文件。右键-打开方式-苹果系统选择文本编辑,Win系统选择记事本 3.按照图示…...

深度学习在老年痴呆检测中的应用:数据集综述
深度学习在老年痴呆检测中的应用:数据集综述 引言 老年痴呆(Alzheimer’s Disease, AD)是一种神经退行性疾病,主要影响老年人,导致记忆力、认知能力和行为的逐步衰退。早期检测和诊断对于延缓疾病进展、提高患者生活质量至关重要。近年来,深度学习技术在医学影像分析和…...
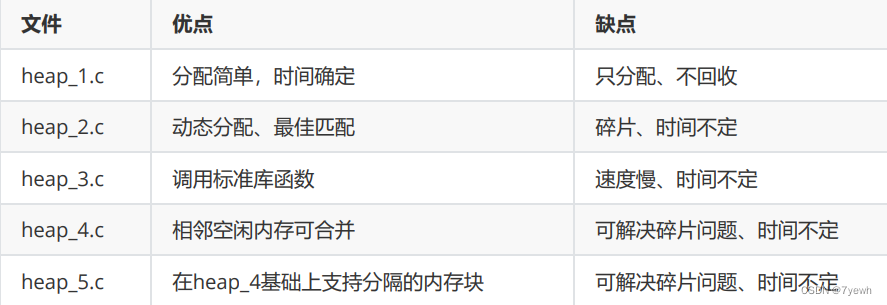
【FreeRTOS】内存管理笔记
一、为什么要自己实现内存管理? 后续的章节涉及这些内核对象:task、queue、semaphores和event group等。为了让FreeRTOS更容 易使用,这些内核对象一般都是动态分配:用到时分配,不使用时释放。使用内存的动态管理功能&…...

【数据结构】二叉树:一场关于节点与遍历的艺术之旅
专栏引入 哈喽大家好,我是野生的编程萌新,首先感谢大家的观看。数据结构的学习者大多有这样的想法:数据结构很重要,一定要学好,但数据结构比较抽象,有些算法理解起来很困难,学的很累。我想让大家…...

arm系统中双网卡共存问题
文章目录 单网卡单独运行双网卡共存问题双网卡解决方案方案一方案二方案三验证双网卡通过网卡名获取IP通过TCP与服务端通信参考单网卡单独运行 双网卡共存问题 双网卡解决方案 方案一 https://blog.csdn.net/HowieXue/article/details/75937972 方案二 http://bbs.witech…...
IDEA创建Mybatis项目
IDEA创建Mybatis项目 第一步:创建库表 -- 创建数据库 create database mybatis_db;-- 使用数据库 use mybatis_db;-- 创建user表 CREATE TABLE user (id INT AUTO_INCREMENT PRIMARY KEY,username VARCHAR(50) NOT NULL,password VARCHAR(50) NOT NULL,email VARC…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
