pip 安装出现 ERROR: Command errored out with exit status 1: 问题解决
使用pip 安装第三方库,前面在升级pip(使用python.exe -m pip install --upgrade pip)也出现如下错误:
ERROR: Command errored out with exit status 1:
command: 'd:\python_3_7_6\python.exe' 'C:\Users\xxxXXXXoooOOOO\AppData\Roaming\Python\Python37\site-packages\pip\_vendor\pep517\_in_process.py' get_requires_for_build_wheel 'C:\Users\xxxXXXXoooOOOO\AppData\Local\Temp\tmpnuowj59l'
cwd: C:\Users\xxxXXXXoooOOOO\AppData\Local\Temp\pip-install-x1eu6x5h\pycryptodome
Complete output (30 lines):
Testing support for clang
Traceback (most recent call last):
File "C:\Users\xxxXXXXoooOOOO\AppData\Roaming\Python\Python37\site-packages\pip\_vendor\pep517\_in_process.py", line 207, in <module>
main()
File "C:\Users\xxxXXXXoooOOOO\AppData\Roaming\Python\Python37\site-packages\pip\_vendor\pep517\_in_process.py", line 197, in main
json_out['return_val'] = hook(**hook_input['kwargs'])
File "C:\Users\xxxXXXXoooOOOO\AppData\Roaming\Python\Python37\site-packages\pip\_vendor\pep517\_in_process.py", line 54, in get_requires_for_build_wheel
return hook(config_settings)
File "C:\Users\xxxXXXXoooOOOO\AppData\Local\Temp\pip-build-env-k8jgz0lh\overlay\Lib\site-packages\setuptools\build_meta.py", line 341, in get_requires_for_build_wheel
return self._get_build_requires(config_settings, requirements=['wheel'])
File "C:\Users\xxxXXXXoooOOOO\AppData\Local\Temp\pip-build-env-k8jgz0lh\overlay\Lib\site-packages\setuptools\build_meta.py", line 323, in _get_build_requires
self.run_setup()
File "C:\Users\xxxXXXXoooOOOO\AppData\Local\Temp\pip-build-env-k8jgz0lh\overlay\Lib\site-packages\setuptools\build_meta.py", line 338, in run_setup
exec(code, locals())
File "<string>", line 490, in <module>
File "C:\Users\xxxXXXXoooOOOO\AppData\Local\Temp\pip-install-x1eu6x5h\pycryptodome\compiler_opt.py", line 333, in set_compiler_options
clang = compiler_is_clang()
File "C:\Users\xxxXXXXoooOOOO\AppData\Local\Temp\pip-install-x1eu6x5h\pycryptodome\compiler_opt.py", line 257, in compiler_is_clang
return test_compilation(source, msg="clang")
File "C:\Users\xxxXXXXoooOOOO\AppData\Local\Temp\pip-install-x1eu6x5h\pycryptodome\compiler_opt.py", line 82, in test_compilation
解决办法:
到 C:\Users\用户名\AppData\Roaming下删除 Python文件夹
到 C:\Users\ppdyh\AppData\Local\Temp 下输出 pip开头的文件夹
相关文章:

pip 安装出现 ERROR: Command errored out with exit status 1: 问题解决
使用pip 安装第三方库,前面在升级pip(使用python.exe -m pip install --upgrade pip)也出现如下错误: ERROR: Command errored out with exit status 1: command: d:\python_3_7_6\python.exe C:\Users\xxxXXXXoooOOOO\AppData…...
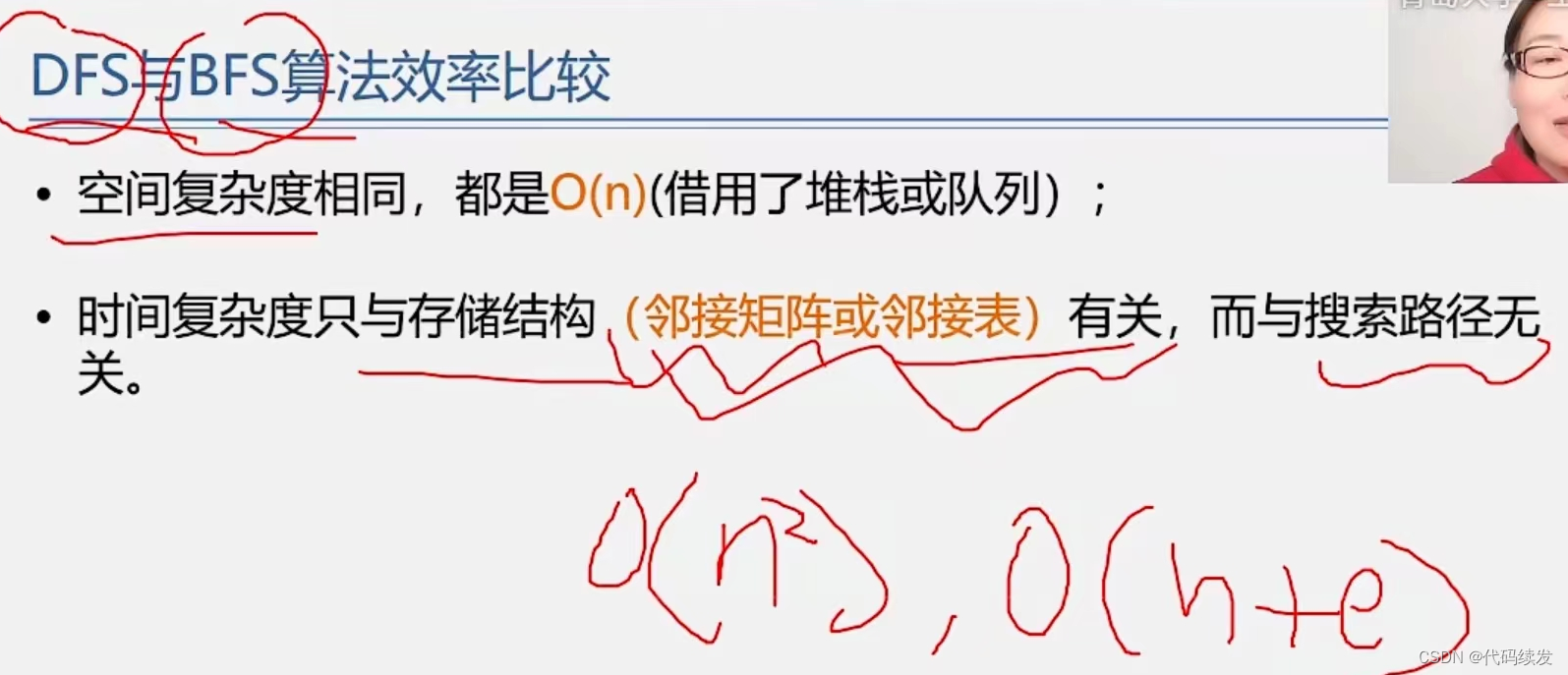
图的遍历介绍
概念 特点 无论是进行哪种遍历,均需要通过设置辅助数组标记顶点是否被访问来避免重复访问!!!! 类型 深度优先遍历 可以实现一次遍历访问一个连通图中的所有顶点,只要连通就能继续向下访问。 因此&#x…...
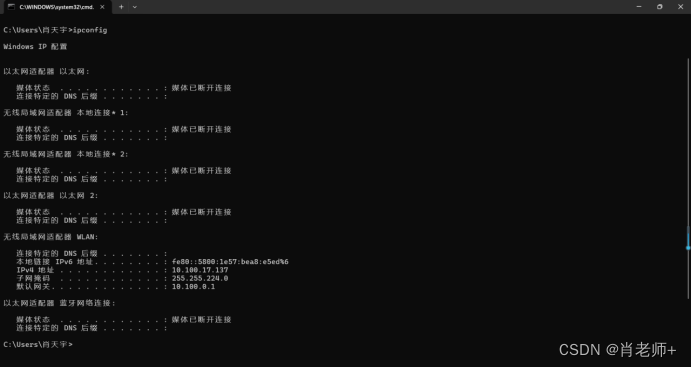
实验二、网络属性设置《计算机网络》
精神状态 be like:边写边崩溃,越写越得劲儿。 目录 一、实验目的: 二、实验内容 三、实验步骤: 四、实验小结 一、实验目的: 掌握 IP 地址、子网掩码等网络属性的设置。 二、实验内容 预备知识: 1、…...
【Python数据魔术】:揭秘类型奥秘,赋能代码创造
文章目录 🚀一.运算符🌈1. 算术运算符🌈2. 身份运算符🌈3. 成员运算符⭐4. 增量运算符⭐5. 比较运算符⭐6. 逻辑运算符 🚀二.可变与不可变🚀三.字符串转义🚀四.编码与解码💥1. 基础使…...
Android Glide loading Bitmap from RESOURCE_DISK_CACHE slow,cost time≈2 seconds+
Android Glide loading Bitmap from RESOURCE_DISK_CACHE slow,cost time≈2 seconds 加载一张宽高约100px多些的小图,是一张相当小的正常图片,loading Bitmap from RESOURCE_DISK_CACHE竟然耗时达到惊人的3秒左右!(打开Glide调试…...
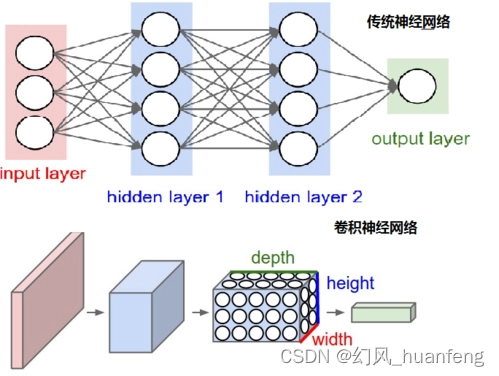
微调技术:人工智能领域的神奇钥匙
在人工智能的浪潮中,深度学习技术凭借其强大的数据处理和学习能力,已成为推动科技进步的重要引擎。然而,深度学习模型的训练往往需要大量的数据和计算资源,这在某些特定场景下成为了限制其发展的瓶颈。为了解决这个问题࿰…...

MyBatis 参数上的处理的细节内容
1. MyBatis 参数上的处理的细节内容 文章目录 1. MyBatis 参数上的处理的细节内容2. MyBatis 参数上的处理3. 准备工作4. 单个(一个)参数4.1 单个(一个)简单类型作为参数4.2 单个(一个) Map集合 作为参数4.3 单个(一个) 实体类POJO作为参数 5. 多个参数5.1 Param注解(命名参数)…...

水帘降温水温
不同环境下的水帘啊,使用水温是不一样的,夏天使用水疗的水有两种,一个是常温的循环水,20~26左右,另外一个呢,就是深井水,重点是啥呢?就是无论我们用哪一种,能够把温度降到…...

kafka如何保证消息不丢失
Kafka发送消息是异步发送的,所以我们不知道消息是否发送成功,所以会可能造成消息丢失。而且Kafka架构是由生产者-服务器端-消费者三种组成部分构成的。要保证消息不丢失,那么主要有三种解决方法。 生产者(producer)端处理 生产者默认发送消息…...

流媒体学习之路(WebRTC)——音频NackTracker优化思路(8)
流媒体学习之路(WebRTC)——音频NackTracker优化思路(8) —— 我正在的github给大家开发一个用于做实验的项目 —— github.com/qw225967/Bifrost目标:可以让大家熟悉各类Qos能力、带宽估计能力,提供每个环节关键参数调节接口并实…...
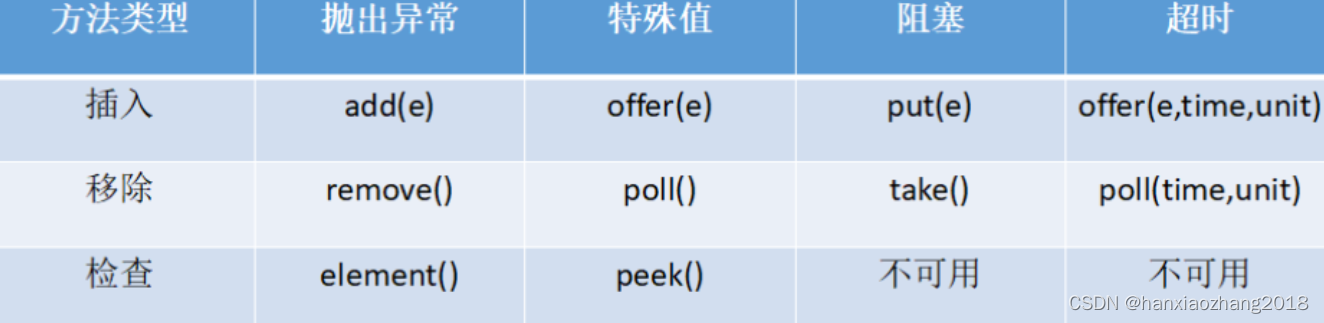
Java基础面试重点-2
21. JVM是如何处理异常(大概流程)? 如果发生异常,方法会创建一个异常对象(包括:异常名称、异常描述以及异常发生时应用程序的状态),并转交给JVM。创建异常对象,并转交给…...

【活动文章】通用大模型VS垂直大模型,你更青睐哪一方
垂直大模型和通用大模型各有其特定的应用场景和优势。垂直大模型专注于特定领域,提供深度的专业知识和技能,而通用大模型则具备广泛的适用性和强大的泛化能力。以下是一些垂直大模型和通用大模型的例子: 垂直大模型 BERT-Financial…...

记录一个Qt调用插件的问题
问题背景 使用Qt主程序插件的方式开发,即主程序做成一个框,定义好插件接口,然后主程序上通过插件接口与插件进行交互。调试过程中遇到了两个问题,在这里记录一下。 问题1(信号槽定义) 插件与主程序之间&am…...

9.1 Go 接口的定义
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「stormsha的主页」…...

易于上手的requests
Python中的requests库主要用于发送HTTP请求并获取响应结果。在现代网络编程中,HTTP请求是构建客户端与服务器之间通信的基础。Python作为一种高级编程语言,其丰富的库支持使得它在网络数据处理领域尤为突出。其中,requests库以其简洁、易用的…...
【QT Creator软件】解决中文乱码问题
QT Creator软件解决中文乱码问题 问题描述:Qtcreator安装好后打印中文在控制台输出乱码 在网上也查找了修改编辑器的默认编码为UTF-8,但是仍然没有任何作用,于是有了以下的解决方案 原因剖析:因为项目的编码与控制台的编码不一致…...
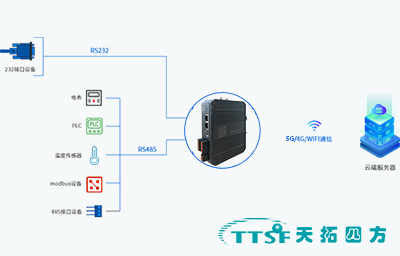
边缘网关在智能制造工厂中的创新应用及效果-天拓四方
在数字化浪潮席卷之下,智能制造工厂正面临着前所未有的数据挑战与机遇。边缘网关,作为数据处理与传输的关键节点,在提升工厂运营效率、确保数据安全方面发挥着日益重要的作用。本文将通过一个具体案例,详细阐述边缘网关在智能制造…...

Django-filter
准备工作 首先,确保你已经安装了django-filter包。如果没有,请使用以下命令安装: pip install django-filter然后,在你的settings.py文件中添加django_filters到INSTALLED_APPS列表中: INSTALLED_APPS [# ...djang…...

文字悬停效果
文字悬停效果 效果展示 CSS 知识点 CSS 变量使用回顾-webkit-text-stroke 属性的运用与回顾 页面整体结构实现 <ul><li style"--clr: #e6444f"><a href"#" class"text">First</a></li><li style"--cl…...
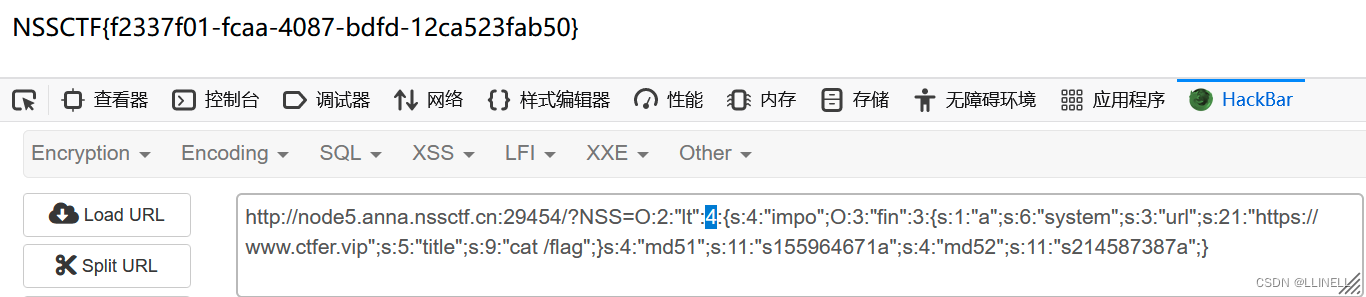
[SWPUCTF 2022 新生赛]ez_1zpop(php反序列化之pop链构造)
[SWPUCTF 2022 新生赛]ez_ez_unserialize <?php class X {public $x __FILE__;function __construct($x){$this->x $x; }function __wakeup(){if ($this->x ! __FILE__) {$this->x __FILE__; }}function __destruct(){highlight_file($this->x);//flag is…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
