【java】【python】leetcode刷题记录--二叉树
144.二叉树的前序遍历
题目链接
前、中、后的遍历的递归做法实际上都是一样的,区别就是遍历操作的位置不同。
对于先序遍历,也就是先根,即把查看当前结点的操作放在最前面即可。
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();preorder(root,res);return res;}public void preorder(TreeNode root, List<Integer> result) {if (root == null) {return;}result.add(root.val);preorder(root.left, result);preorder(root.right, result);}
}
而中序和后序遍历也是一样:
// 中序
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();midorder(root,res);return res;}public void midorder(TreeNode root, List<Integer> res){if(root == null){return;}midorder(root.left,res);res.add(root.val);midorder(root.right,res);}
}
//后序
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();postorder(root,res);return res;}public void postorder(TreeNode root, List<Integer> res){if(root == null){return;}postorder(root.left,res);postorder(root.right,res);res.add(root.val);}
}
python版本也一样,这里就写一种:
class Solution:def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:res = []def dfs(root):if root is None:return dfs(root.left)dfs(root.right)res.append(root.val)dfs(root) # 调用dfs函数开始遍历return res
如果不用递归,那会有一点麻烦,但也仅仅是代码上的。因为递归本身就是借用系统栈,而使用迭代则是自己创建栈进行操作即可。
前序则是将根节点入栈,后续的结点是按照先右边再左边的顺序入栈(因为我们要先处理左子,因此左子后入栈可以先被pop)。
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();if (root == null){return res;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while(!stack.isEmpty()){TreeNode tmp = stack.pop();res.add(tmp.val);if(tmp.right != null){stack.push(tmp.right);}if(tmp.left != null){stack.push(tmp.left);}}return res;}
}
但中后序的操作和前序不太一样(虽然有方法可以进行统一,但本文不赘述)。而后序则是将先序(根左右)进行操作(根左右->根右左->左右根),即调整处理顺序+反转数组。
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null){return result;}Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;while (cur != null || !stack.isEmpty()){if (cur != null){stack.push(cur);cur = cur.left;}else{cur = stack.pop();result.add(cur.val);cur = cur.right;}}return result;}
}
102 二叉树的层序遍历
题目链接
层序遍历用的是队列,每次将一个节点入队,处理完当前节点,则其子节点分别入队,下一轮再处理子节点,也就是下一层的内容。
例如,一棵树为1、2、3、4、5(数组表示),那么第一次是1入队,处理完1后,1的子节点也就是2、3入队。处理完2,也就是2的子节点入队,即4、5。3处理后没有子节点,就剩下4、5需要处理。
如果是要求返回的是一个列表,没有嵌套结构,那就会好做很多,我们就按照上面的流程构造队列然后不断处理即可。但现在返回的要求是每一层都要有一个单独的列表,因此就麻烦一些。
我们就使用两重循环,第一重是记录队列是否为空,第二重则是看当前遍历的层。
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<TreeNode> deque = new LinkedList<>();List<List<Integer>> res = new ArrayList<List<Integer>>();if(root == null){return res;}deque.add(root);while(!deque.isEmpty()){// len记录当前层的个数,tmpList则是存放当前层,最后统一add到res上int len = deque.size();List<Integer> tmpList = new ArrayList<>();while(len>0){TreeNode tmpNode = deque.removeFirst();tmpList.add(tmpNode.val);if(tmpNode.left!=null){deque.add(tmpNode.left);}if(tmpNode.right!=null){deque.add(tmpNode.right);}len--;}res.add(tmpList);}return res;}
}
相关文章:

【java】【python】leetcode刷题记录--二叉树
144.二叉树的前序遍历 题目链接 前、中、后的遍历的递归做法实际上都是一样的,区别就是遍历操作的位置不同。 对于先序遍历,也就是先根,即把查看当前结点的操作放在最前面即可。 class Solution {public List<Integer> preorderTrav…...
EVA-CLIP实战
摘要 EVA-CLIP,这是一种基于对比语言图像预训练(CLIP)技术改进的模型,通过引入新的表示学习、优化和增强技术,显著提高了CLIP的训练效率和效果。EVA-CLIP系列模型在保持较低训练成本的同时,实现了与先前具有相似参数数量的CLIP模型相比更高的性能。特别地,文中提到的EV…...

限定法术施放目标
实现目标 法术只对特定 creature | gameobject 施放,否则无法施放 实现方法 conditions SourceTypeOrReferenceId:13(CONDITION_SOURCE_TYPE_SPELL_IMPLICIT_TARGET)SourceGroup:受条件影响的法术效果掩码…...

【通信原理】数字频带传输系统
二进制数字调制,解调原理:2ASK,2FSK 二进制数字调制,解调原理:2PSK,2DPSK 二进制数字已调制信号的功率谱 二进制数字调制系统的抗噪声性能 二进制调制系统的性能总结...
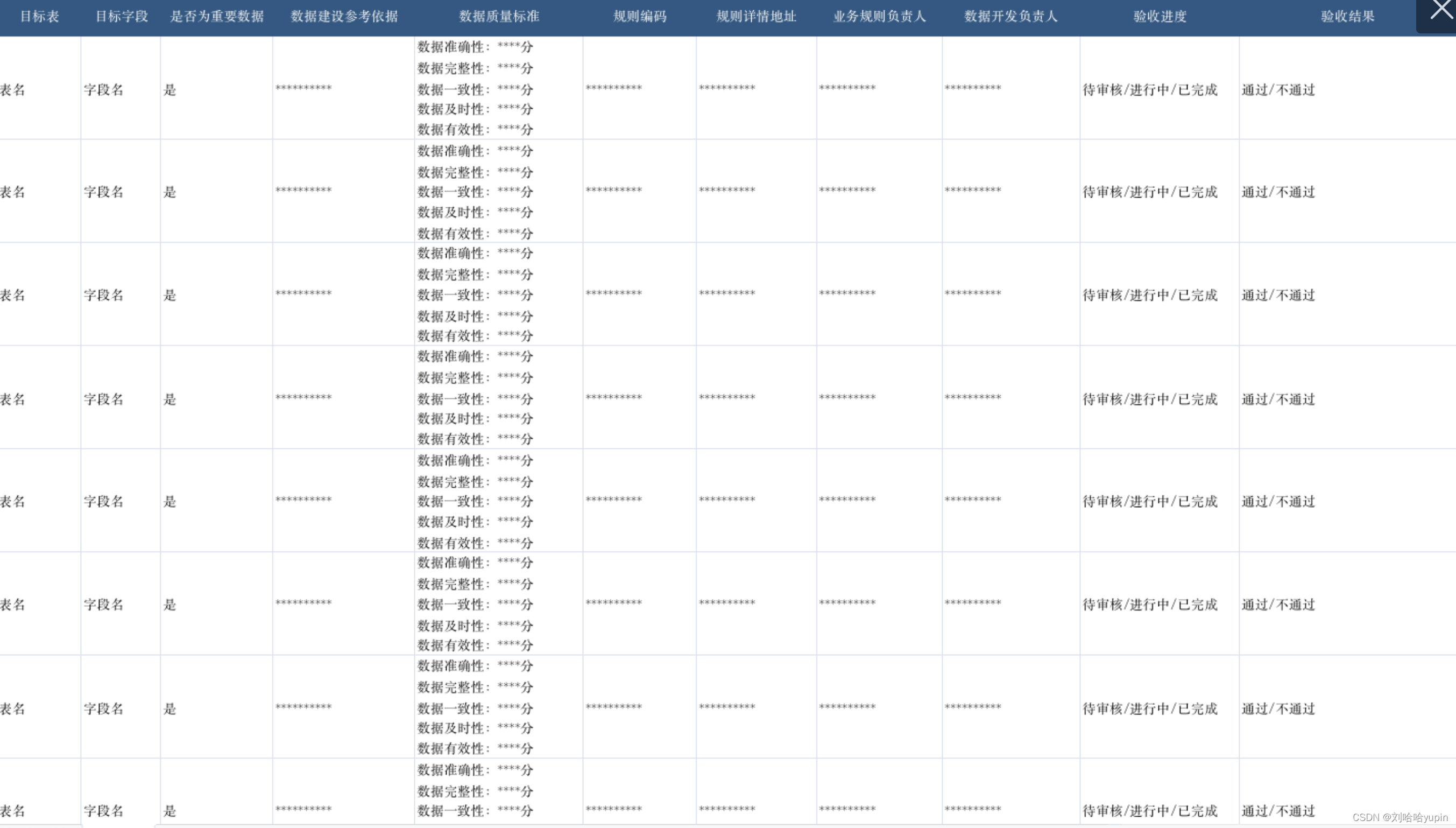
数据价值管理-数据验收标准
前情提要:数据价值管理是指通过一系列管理策略和技术手段,帮助企业把庞大的、无序的、低价值的数据资源转变为高价值密度的数据资产的过程,即数据治理和价值变现。第一讲介绍了业务架构设计的基本逻辑和思路。前面我们讲完了数据资产建设标准…...

vue3模板语法总结
1. 响应式数据 Vue 3中的数据是响应式的,即当数据发生变化时,视图会自动更新。这是通过使用JavaScript的getter和setter来实现的。 2. 组件化 Vue 3采用组件化开发方式,允许创建可复用的组件。 每个组件都有自己的作用域,并且…...
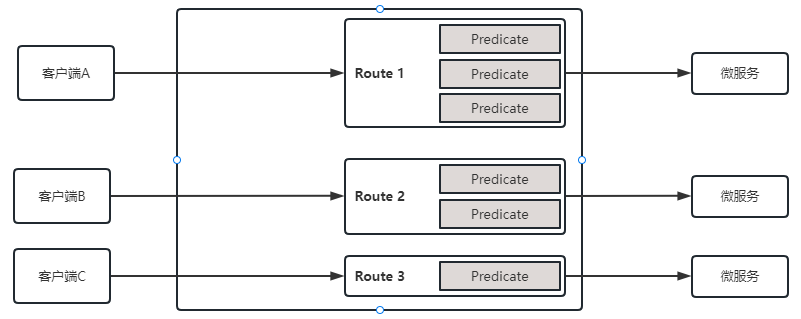
Spring Cloud 之 GateWay
前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家:https://www.captainbed.cn/z ChatGPT体验地址 文章目录 前言前言1、通过API网关访问服务2、Spring Cloud GateWay 最主要的功能就是路由…...

可转债全部历史因子数据,提供api支持
今天在写可转债系统,顺便下载了一下服务器的可转债数据,给大家研究使用 from trader_tool.stock_data import stock_datafrom trader_tool.lude_data_api import lude_data_apiimport osclass convertible_bond_back_test_system: 可转债回测系统…...

Python | C++ | MATLAB | Julia | R 市场流动性数学预期评估量
🎯要点 🎯市场流动性策略代码应用:🎯动量策略:滚动窗口均值策略、简单移动平均线策略、指数加权移动平均线策略、相对强弱指数、移动平均线收敛散度交叉策略、三重指数平均策略、威廉姆斯 %R 策略 | 🎯均值…...

Android 常用开源库 MMKV 源码分析与理解
文章目录 前言一、MMKV简介1.mmap2.protobuf 二、MMKV 源码详解1.MMKV初始化2.MMKV对象获取3.文件摘要的映射4.loadFromFile 从文件加载数据5.数据写入6.内存重整7.数据读取8.数据删除9.文件回写10.Protobuf 实现1.序列化2.反序列化 12.文件锁1.加锁2.解锁 13.状态同步 总结参考…...
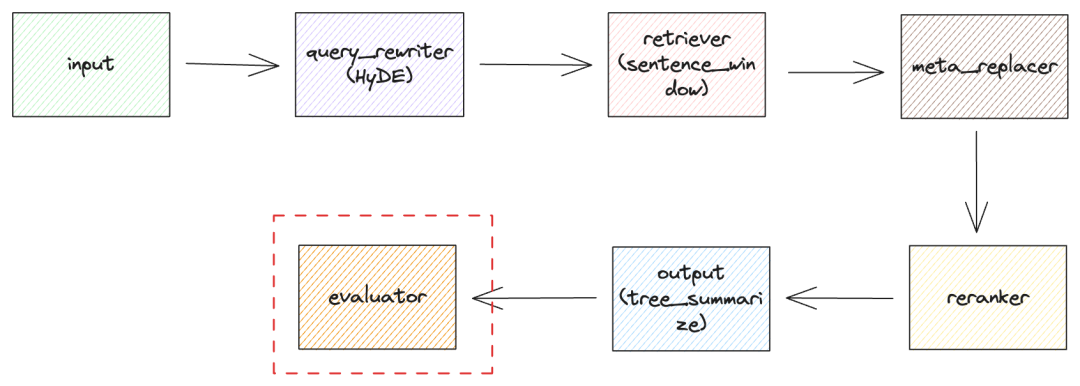
大模型高级 RAG 检索策略之流程与模块化
我们介绍了很多关于高级 RAG(Retrieval Augmented Generation)的检索策略,每一种策略就像是机器中的零部件,我们可以通过对这些零部件进行不同的组合,来实现不同的 RAG 功能,从而满足不同的需求。 今天我们…...

TCPListen客户端和TCPListen服务器
创建项目 TCPListen服务器 public Form1() {InitializeComponent();//TcpListener 搭建tcp服务器的类,基于socket套接字通信的//1创建服务器对象TcpListener server new TcpListener(IPAddress.Parse("192.168.107.83"), 3000);//2 开启服务器 设置最大…...

DDei在线设计器-属性编辑器
DDei-Core-属性编辑器 DDei-Core-属性编辑器插件包含了文本、大文本、数值、下拉、单选、勾选以及颜色等属性编辑。 图形和属性共同构成一个完整的定义,属性编辑器就是编辑属性值的控件。当选中图形实例时,属性面板就会展现当前实例的所有属性以及属性编…...

八字综合测算网整站源码程序/黄历/灵签/排盘/算命/生肖星座/日历网/周公解梦
八字综合测算网整站源码程序/黄历/灵签/排盘/算命/生肖星座/日历网/周公解梦 演示地址: https://s24.gvyun.com/ 手机端地址: https://ms24.gvyun.com/ 网站功能分类: 八字:八字测算;日干论命;称骨论命…...
—— 布局管理)
C# WPF入门学习主线篇(十一)—— 布局管理
C# WPF入门学习主线篇(十一)—— 布局管理 欢迎来到C# WPF入门学习系列的第十一篇。在前面的文章中,我们已经探讨了WPF中的许多控件及其属性和事件。今天,我们将开启一个新的篇章——布局管理。布局管理是WPF中一个至关重要的概念…...

LabVIEW轴承试验机测控系统
开发了一种基于LabVIEW软件开发的大功率风电机组增速箱轴承试验机测控系统。系统主要用于模拟实际工况,进行轴承可靠性分析,以优化风电机组的性能和可靠性。通过高度自动化的测控系统,实现了对试验机的精确控制,包括速度、振动、温…...
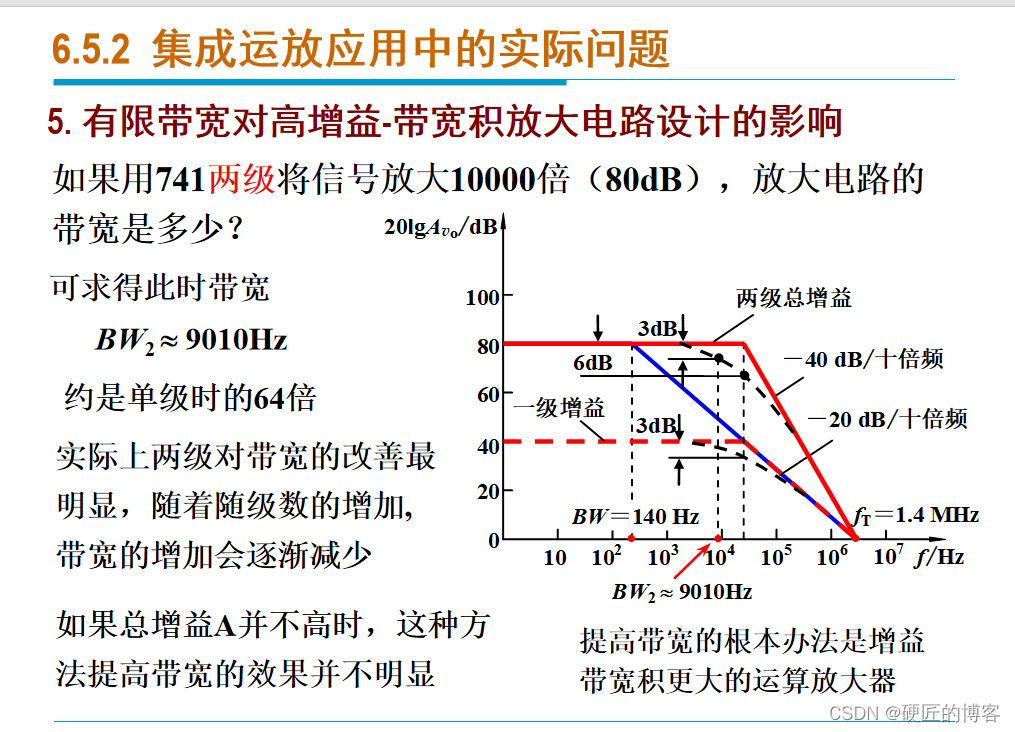
0605 实际集成运算放大器的主要参数和对应用电路的影响
6.5.1 实际集成运放的主要参数 6.5.2 集成运放应用中的实际问题 6.5.2 集成运放应用中的实际问题...
艾宾浩斯winform单词系统+mysql
为用户提供集词典、题库、记忆单词功能于一体的应用,为用户提供目的性强、科学高效、多样化的记忆单词方法,使用户学习英语和记忆单词的效率得到提高 单词记忆模块 管理模块 查询单词 阅读英文 查看词汇 记忆单词 收藏单词 字段管理设置 统计 艾宾浩斯wi…...

rv1126-rv1109-串口显示路径不变化
串口只有#, 后来看了教程改成如下 但是没有变化,那个路径都只显示rootLonbon# 于是最后改成了这样 因为:...

基于C#开发web网页管理系统模板流程-主界面密码维护功能完善
点击返回目录-> 基于C#开发web网页管理系统模板流程-总集篇-CSDN博客 前言 紧接上篇->基于C#开发web网页管理系统模板流程-主界面统计功能完善-CSDN博客 一个合格的管理系统,至少一定存在一个功能——用户能够自己修改密码,理论上来说密码只能有用…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
