动态规划法学习
当然,让我们用更生活化的语言和一个实际的例子来解释动态规划,以及如何在实践中应用它。
动态规划通俗理解
想象一下,你是个水果摊老板,每天要决定订购多少苹果,目标是最大化利润。但苹果的价格每天波动,顾客的需求也变化,你该怎么办?
传统做法:每天早上,你都根据昨天的经验和今天的感觉猜测需求,然后订购苹果。但如果猜错,要么苹果卖不完亏本,要么不够卖错过赚钱机会。
动态规划做法:你开始记录每一天的销售数据,包括苹果价格、天气、节假日等因素。第二天,你不再凭感觉,而是根据历史数据预测需求,再决定订购量。因为你“记得”过去的经验,所以可以做出更精准的决策,减少浪费,增加利润。
实践过程详解
以经典的背包问题为例,假设你是个旅行者,背包容量有限,你要从一堆物品中选择装入背包,每件物品有重量和价值,你的目标是让背包里物品的总价值最大,但不超过背包容量。
步骤1:定义问题
- 状态:背包当前的剩余容量,已经选了哪些物品。
- 目标:背包内物品价值最大化。
步骤2:构建状态转移方程
- 假设 d p [ i ] [ j ] dp[i][j] dp[i][j]表示前i件物品装入容量为j的背包中的最大价值。
- 状态转移方程为: d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − w e i g h t [ i ] ] + v a l u e [ i ] ) dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i]) dp[i][j]=max(dp[i−1][j],dp[i−1][j−weight[i]]+value[i]),其中 w e i g h t [ i ] weight[i] weight[i]和 v a l u e [ i ] value[i] value[i]分别是第i件物品的重量和价值。
状态定义
我们定义 d p [ i ] [ j ] dp[i][j] dp[i][j]表示考虑前 i i i个物品,且背包容量为 j j j时,所能达到的最大价值。
状态转移方程
状态转移方程是这样的:
d p [ i ] [ j ] = max ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − w i ] + v i ) dp[i][j] = \max(dp[i-1][j], dp[i-1][j-w_i] + v_i) dp[i][j]=max(dp[i−1][j],dp[i−1][j−wi]+vi)
这里:
- d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j] 表示不拿第 i i i个物品,此时最大价值就是前 i − 1 i-1 i−1个物品在容量为 j j j的背包下的最大价值。
- d p [ i − 1 ] [ j − w i ] + v i dp[i-1][j-w_i] + v_i dp[i−1][j−wi]+vi表示拿了第 i i i个物品,此时背包剩余容量为 j − w i j-w_i j−wi( w i w_i wi是第$ 个物品的重量),然后加上第 个物品的重量),然后加上第 个物品的重量),然后加上第i$个物品的价值 v i v_i vi 。
方程解读
这个方程意味着我们在考虑第 i i i个物品时,有两种选择:
- 不拿第 i i i个物品:此时最大价值取决于前 i − 1 i-1 i−1个物品在容量为 j j j的背包下能达到的最大价值,即 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]。
- 拿第 i i i个物品:此时我们需要确保背包容量足够装下这个物品,即 j > = w i j >= w_i j>=wi。在这种情况下,我们的最大价值由前 i − 1 i-1 i−1个物品在剩余容量 j − w i j-w_i j−wi下的最大价值加上第 i i i个物品的价值组成,即 d p [ i − 1 ] [ j − w i ] + v i dp[i-1][j-w_i] + v_i dp[i−1][j−wi]+vi。
最终,我们取这两种选择中价值更大的那个作为 d p [ i ] [ j ] dp[i][j] dp[i][j]的值。
步骤3:初始化边界条件
- 当背包容量为0或没有物品时,价值为0,即 d p [ 0 ] [ j ] = 0 dp[0][j] = 0 dp[0][j]=0和 d p [ i ] [ 0 ] = 0 dp[i][0] = 0 dp[i][0]=0。
步骤4:计算
- 从 d p [ 0 ] [ 0 ] dp[0][0] dp[0][0]开始,按行或列递增地填充整个二维数组,直到得到 d p [ n ] [ W ] dp[n][W] dp[n][W],即为所求的最大价值。
实践注意点
- 状态定义要准确:状态必须包含足够的信息来描述问题,但又不能过于复杂,否则计算量会很大。
- 避免重复计算:动态规划的核心是记忆化,即保存已计算的状态,避免重复计算相同的子问题。
- 边界条件:正确的边界条件是关键,否则可能导致整个解法失效。
- 空间优化:有时可以通过观察状态转移方程,仅保留必要的状态信息,减少内存消耗。
结语
动态规划就像一个智慧的决策者,它通过分析过去的“经验”(子问题的解),来做出更好的“未来决策”(解决大问题)。在实践中,清晰的状态定义、有效的状态转移方程和合理的边界条件是成功应用动态规划的关键。希望这次解释能帮助你更好地理解和掌握动态规划!
相关文章:

动态规划法学习
当然,让我们用更生活化的语言和一个实际的例子来解释动态规划,以及如何在实践中应用它。 动态规划通俗理解 想象一下,你是个水果摊老板,每天要决定订购多少苹果,目标是最大化利润。但苹果的价格每天波动,…...

前端技术回顾系列 10|TS 泛型在类和接口中的应用
在微信中阅读,关注公众号:CodeFit。 创作不易,如果你觉得这篇文章对您有帮助,请不要忘了 点赞、分享 和 关注 我的公众号:CodeFit,为我的持续创作提供动力。 上文回顾:约束泛型(Generic Constraints) 上一篇文章我们回顾了 泛型 在 TypeScript 中的高级用法 —— 泛型…...
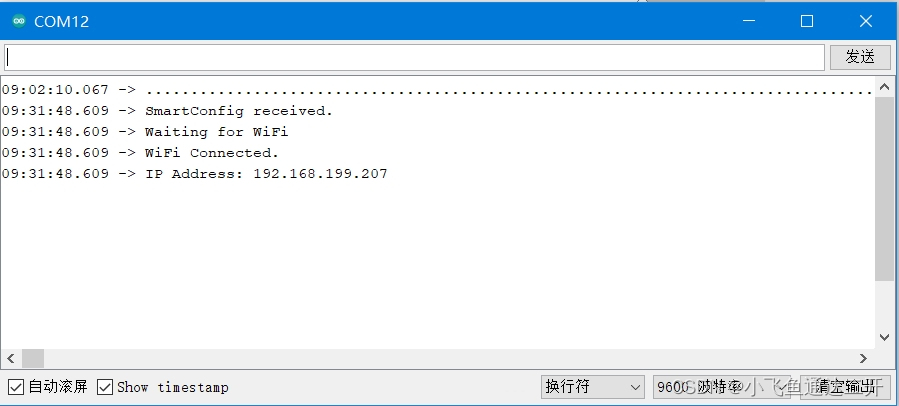
【Ardiuno】实验ESP32单片机自动配置Wifi功能(图文)
这里小飞鱼按照ESP32的示例代码,实验一下wifi的自动配置功能。所谓的自动配置,就是不用提前将wifi的名称和密码写到程序里,这样可以保证程序在烧录上传后,可以通过手机端的软件来进行配置,可以避免反复修改代码&#x…...

xml数据解析
XML Pull Parser(使用Android的XmlPullParser) 原理 Pull Parser允许应用程序代码从XML数据中“拉取”事件,而不是像SAX那样通过事件处理程序被“推送”。应用程序代码可以决定何时拉取下一个事件,如开始元素、结束元素或文本内…...

vite工程化搭建vue项目之自动按需导入
背景 当我们在使用vue3组合式开发的时候,大多数情况下我们的代码可能是这样的 <script setup lang"ts"> import { ref, reactive, toRefs, onMounted, computed } from vue; defineProps({}); </script><template><div></di…...
yolo-inference多后端+多任务+多算法+多精度模型 框架开发记录(python版)
先贴出github地址,欢迎大家批评指正:https://github.com/taifyang/yolo-inference 不知不觉LZ已经快工作两年了,由于之前的工作内容主要和模型部署相关,想着利用闲暇时间写一些推理方面的经验总结,于是有了这个工程。其…...

uniapp使用vue3语法构建自定义导航栏,适配小程序胶囊
具体代码 <template><view class"nav-wrapper-container" :style"height:navBarHeight px"><view class"nav-status-container" :style"height:navstatusBarHeight px;" /><view v-if"isCustom" clas…...

wpf、winform 监听USB拔插时触发
C# USB拔插监听 C#查找设备管理器中所有的 USB 设备 wpf、winform 监听USB拔插时触发 监听Windows USB 拔插时触发 private void MainWindow_Loaded(object sender, RoutedEventArgs e){FleckWebSocketConfig.OpenSocketConfig().GetAwaiter(); //websocket 服务开启用于监听W…...

C语言:指针笔试题
// 输入某一年的第几天,计算并输出它是这一年的第几月第几日。 /* 函数功能: 对给定的某一年的第几天,计算它是这一年的第几月第几日。 函数入口参数: 整形变量year,存储年; 整形变量yearDay,存储某一年的第几天&am…...

搜维尔科技:Movella旗下的Xsens在人形机器人开发中得到广泛应用
人形机器人的发展正在全球范围内受到广泛关注。作为机器人领域的重要分支,人形机器人因其具备高度仿真的外观和动作,以及更贴近人类的行为模式,有望逐渐成为人们日常生活和工业生产中的得力助手。在中国,这一领域的发展尤为引人注…...

k8s学习--kubernetes服务自动伸缩之水平伸缩(pod副本伸缩)HPA详细解释与案例应用
文章目录 前言HPA简介简单理解详细解释HPA 的工作原理监控系统负载模式HPA 的优势使用 HPA 的注意事项应用类型 应用环境1.metircs-server部署2.HPA演示示例(1)部署一个服务(2)创建HPA对象(3)执行压测 前言…...

Mock数据
Mock 数据 引入依赖 <dependency><groupId>com.github.jsonzou</groupId><artifactId>jmockdata</artifactId><version>4.3.0</version></dependency>mock 数据 MockConfig mockConfig new MockConfig().sizeRange(1, 1);A.…...

【MySQL】性能分析
https://www.bilibili.com/video/BV1Kr4y1i7ru/?p78 查看执行频次 查看当前数据库的 INSERT, UPDATE, DELETE, SELECT 访问频次: SHOW GLOBAL STATUS LIKE Com_______; 或者 SHOW SESSION STATUS LIKE Com_______; 慢查询日志 慢查询日志记录了所有执行时间超过指…...
MyBatis插件机制
MyBatis插件机制是该框架提供的一种灵活扩展方式,允许开发者在不修改框架源代码的情况下对MyBatis的功能进行定制和增强。这种机制主要通过拦截器(Interceptor)实现,使得开发者可以拦截和修改MyBatis在执行SQL语句过程中的行为。 …...

NVIDIA Jetson Linux 35.3.1-开发指南-导言
原文地址:Welcome — Jetson Linux Developer Guide documentation (nvidia.com) 欢迎 本开发人员指南适用于 NVIDIA Jetson Linux版本 35.3.1 GA 。 最后更新: 2023年5月19日 NVIDIA Jetson是世界领先的边缘AI平台。其高性能、低功耗计算 深度学习 ,…...

14. fastLED调色板
Color Palettes Functions and class definitions for color palettes.调色板的函数和类定义。 RGB palettes map an 8-bit value (0-255) to an RGB color. You can create any color palette you wish; a couple of starters are provided: ForestColors_p, CloudColors_p…...
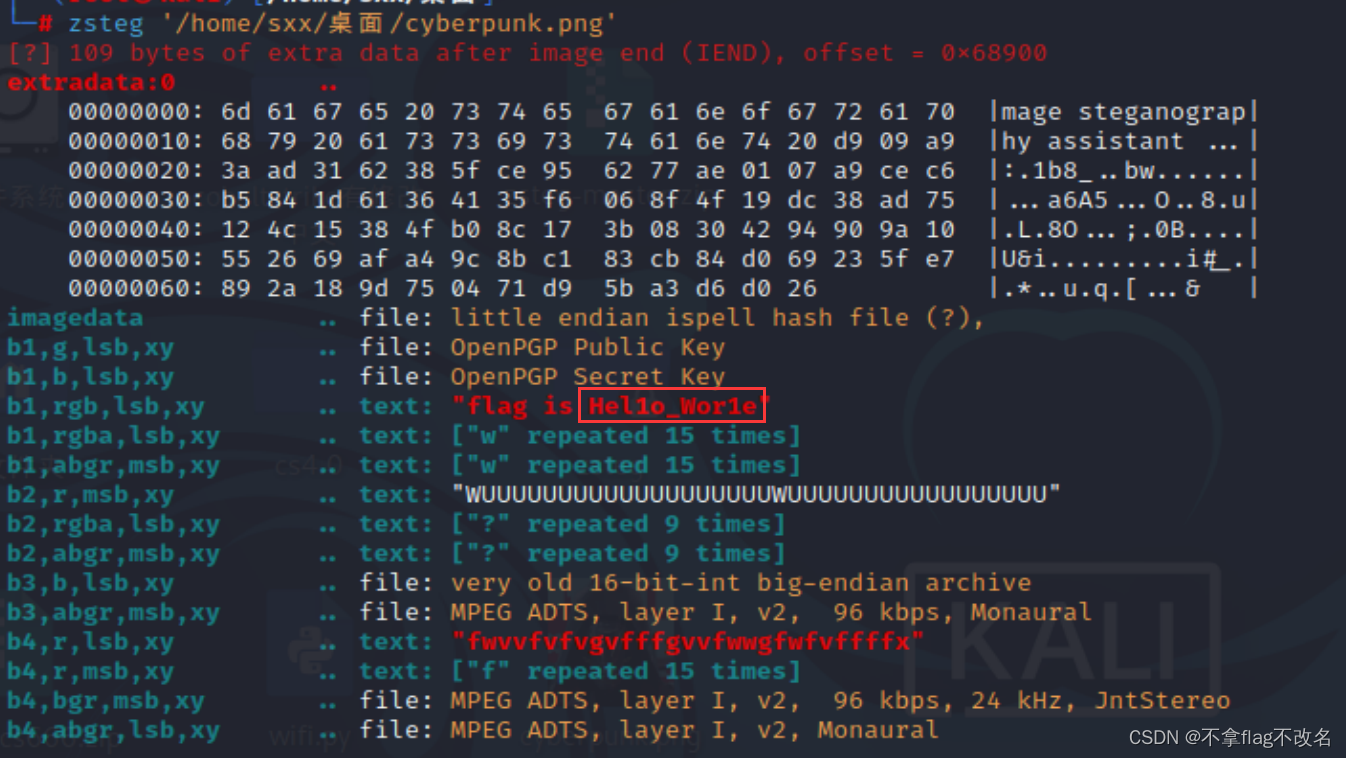
bugku---misc---赛博朋克
1、下载附件解压之后是一个txt文本,查看文本的时候看到头部有NG的字样 2、把txt改为png后缀得到一张图片 3、binwalk没发现奇怪的地方,分离出来还是图片 4、stegslove分析,切换图片没有发现奇怪地方 5、将通道rgb置为0。出现了flag但是flag不…...
vue+elementplus模拟“山野愚人居”简单实现个人博客
目录 一、项目介绍 二、项目截图 1.项目结构图 2.项目首页 3.文章详情 4.留言 5.读者 三、源码实现 1.项目依赖package.json 2.项目启动 3.读者页面源码 四、总结 一、项目介绍 模仿原博客:山野愚人居 - 记录我的生活、所见、所闻、所想…… 本项目参考以…...

ComfyUI 完全入门:Refiner精炼器
在 SDXL基础模型1.0版本发布时,Stability AI 公司同时发布了一个名为SDXL Refiner的模型。这个Refiner模型是专门设计用来对基础模型生成的图像进行进一步优化和细化的,所以大家也经常称之为精炼器或者精修器。 Refiner模型的主要目的是提升图像的质量&…...
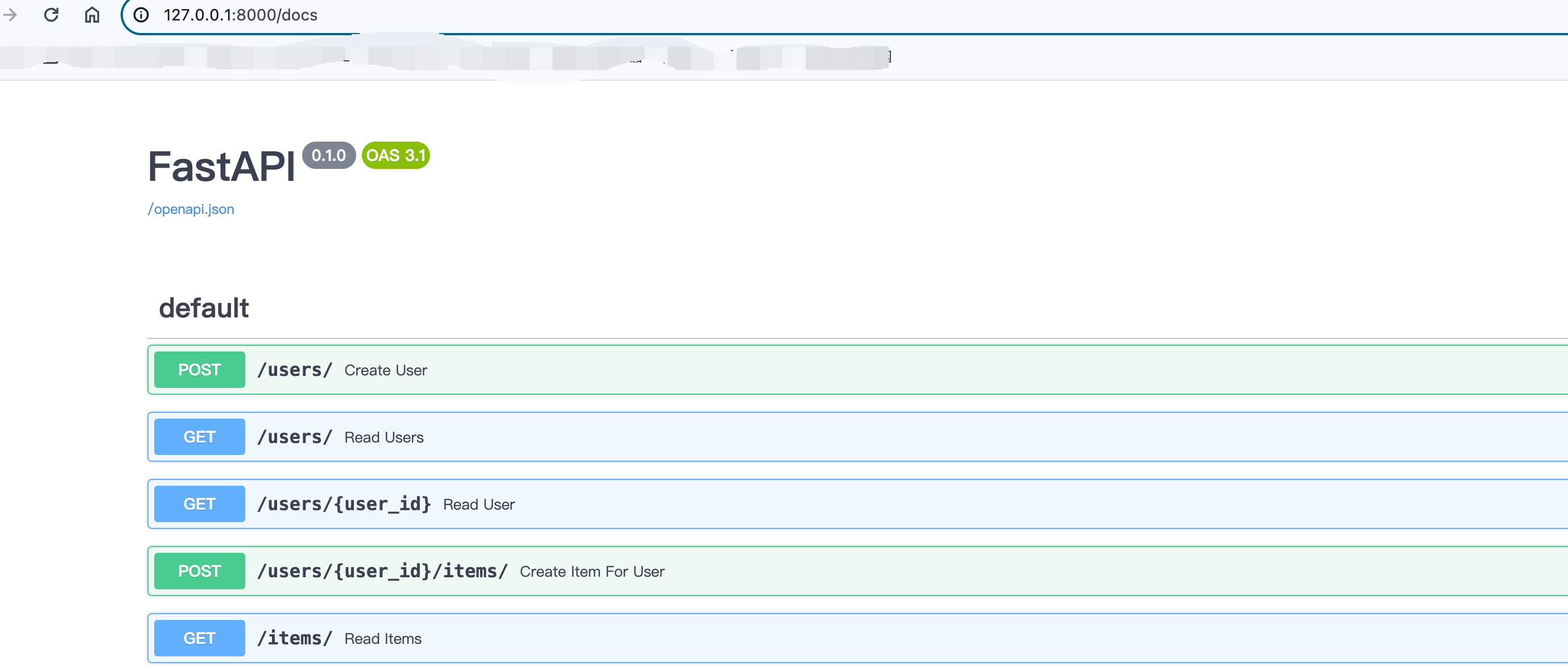
FastAPI操作关系型数据库
FastAPI可以和任何数据库和任意样式的库配合使用,这里看一下使用SQLAlchemy的示例。下面的示例很容易的调整为PostgreSQL,MySQL,SQLite,Oracle等。当前示例中我们使用SQLite ORM对象关系映射 FastAPI可以与任何数据库在任何样式…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
