LeetCode-416. 分割等和子集
目录
- 题目分析
- 回溯法
- 动态规划
- 动态规划(压缩)
题目来源
416. 分割等和子集
题目分析
这道题目是要找是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
那么只要找到集合里能够出现 sum / 2 的子集总和,就算是可以分割成两个相同元素和子集了。
回溯法
这道题和39. 组合总和非常类似(可以去做一下)
LeetCode-39. 组合总和
class Solution {boolean res;public boolean canPartition(int[] nums) {int sum = 0;for(int i = 0;i<nums.length;i++){sum += nums[i];}//如果为奇数,肯定就没有两个相等的子集了if(sum % 2 == 1){return false;}//查找目标target的子集和int target = sum / 2;backTracking(nums,0,0,target);return res;}//startIndex为了数组不选取重复元素,sum为加起来的总和,target目标数private void backTracking(int[] nums,int startIndex,int sum,int target){//如果sum>target就没必要进行计算了if(sum > target){return;}//如果等于,直接将res设置为为true,相当于是相同子集了if(sum == target){res = true;return;}for(int i = startIndex;i<nums.length;i++){sum+=nums[i];backTracking(nums,i+1,sum,target);sum-=nums[i]; //回溯}}
}
这道题使用回溯算法不行(超时),那么就要用动态规划了
动态规划
背包问题,大家都知道,有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
背包问题有多种背包方式,常见的有:01背包、完全背包、多重背包、分组背包和混合背包等等。
要注意题目描述中商品是不是可以重复放入。
即一个商品如果可以重复多次放入是完全背包,而只能放入一次是01背包,写法还是不一样的。
要明确本题中我们要使用的是01背包,因为元素我们只能用一次。
回归主题:首先,本题要求集合里能否出现总和为 sum / 2 的子集。
那么来一一对应一下本题,看看背包问题如何来解决。
只有确定了如下四点,才能把01背包问题套到本题上来。
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
理解了0-1背包问题,直接搬照着公式就可以写出
https://donglin.blog.csdn.net/article/details/129412502
class Solution {public boolean canPartition(int[] nums) {if(nums == null){return false;}int sum = 0;for(int num : nums){sum += num;}if(sum % 2 == 1){return false;}int target = sum / 2;int[][] dp = new int[nums.length][target+1];for(int j=target;j>=nums[0];j--){dp[0][j] = nums[0];}for(int i = 1;i<nums.length;i++){for(int j = 1;j<=target;j++){if(j<nums[i]){dp[i][j] = dp[i-1][j];}else{dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-nums[i]]+nums[i]);}}}return dp[nums.length-1][target]==target;}
}

动态规划(压缩)
动规五部曲分析如下:
- 1.确定dp数组以及下标的含义
01背包中,dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]。
本题中每一个元素的数值既是重量,也是价值。
套到本题,dp[j]表示 背包总容量(所能装的总重量)是j,放进物品后,背的最大重量为dp[j]。
那么如果背包容量为target, dp[target]就是装满 背包之后的重量,所以 当 dp[target] == target 的时候,背包就装满了。
- 2.确定递推公式
如果不清楚0-1背包问题的一维数组,可以看这篇
https://donglin.blog.csdn.net/article/details/129437136
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
相当于背包里放入数值,那么物品i的重量是nums[i],其价值也是nums[i]。
所以递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
- 3.dp数组如何初始化
在01背包,一维dp如何初始化,已经讲过,
从dp[j]的定义来看,首先dp[0]一定是0。
- 4.确定遍历顺序
如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
for(int i = 0;i<nums.length;i++){for(int j = target;j>=nums[i];j--){dp[j] = Math.max(dp[j],dp[j-nums[i]]+nums[i]);}}
- 5.举例推导dp数组
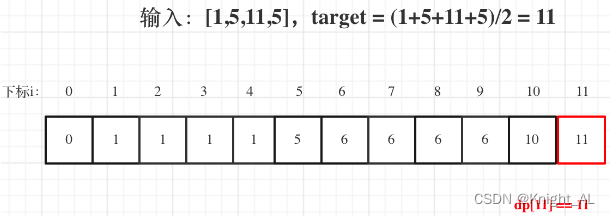
完整代码
class Solution {public boolean canPartition(int[] nums) {if(nums == null){return false;}int sum = 0;for(int num : nums){sum += num;}if(sum % 2 == 1){return false;}int target = sum / 2;int[] dp = new int[target+1];for(int i = 0;i<nums.length;i++){for(int j = target;j>=nums[i];j--){//物品 i 的重量是 nums[i],其价值也是 nums[i]dp[j] = Math.max(dp[j],dp[j-nums[i]]+nums[i]);}}return dp[target] == target;}
}

相关文章:

LeetCode-416. 分割等和子集
目录题目分析回溯法动态规划动态规划(压缩)题目来源 416. 分割等和子集 题目分析 这道题目是要找是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。 那么只要找到集合里能够出现 sum / 2 的子集总和,就算是可以分割成两个相同元素和子集了…...
2021年 第12届 蓝桥杯 Java B组 省赛真题详解及小结【第2场省赛 2021.05.09】
一、试题A:求余(本题总分:5 分) 得:5分 本题总分:5 分 【问题描述】 在 C/C/Java/Python 等语言中,使用 % 表示求余,请问 2021%20 的值是多少? 【答案提交】 这是一道结果…...

elasticSearch写入原理
elasticSearch写入原理 最近学习完了es相关的课程整理除了es的核心内容,学习这东西知其然知其所以然,自己按照自己的理解整理了es相关的面试题。先热个身,整理一下es的写入原理,有不对的地方请大家指正。 这些原理的东西我觉得还是…...
Python)
第十四届蓝桥杯模拟赛(第三期)Python
1 进制转换 问题描述 请找到一个大于 2022 的最小数,这个数转换成十六进制之后,所有的数位(不含前导 0)都为字母(A 到 F)。 请将这个数的十进制形式作为答案提交。 答案:2730 def ch…...

Pytorch模型参数的保存和加载
目录 一、前言 二、参数保存 三、参数的加载 四、保存和加载整个模型 五、总结 一、前言 在模型训练完成后,我们需要保存模型参数值用于后续的测试过程。由于保存整个模型将耗费大量的存储,故推荐的做法是只保存参数,使用时只需在建好模…...
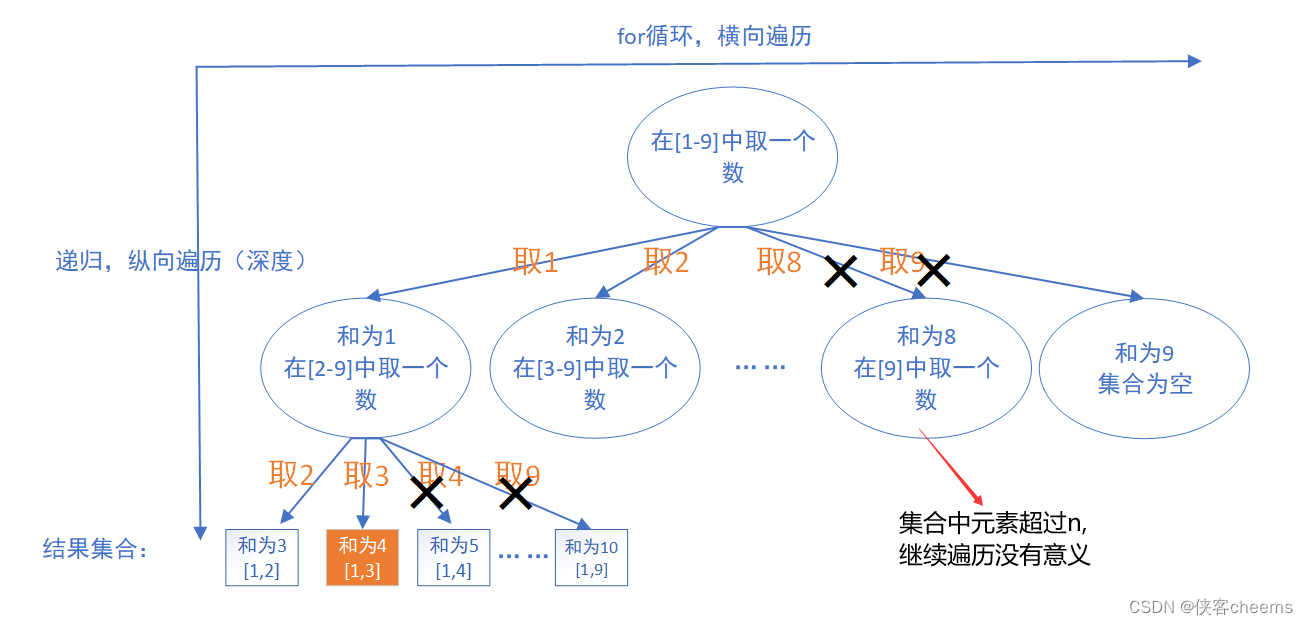
面试热点题:回溯算法之组合 组合与组合总和 III
什么是回溯算法? 回溯算法也可以叫回溯搜索算法,回溯是递归的"副产品",回溯的本质是穷举,然后选出我们需要的数据,回溯本身不是特别高效的算法,但我们可以通过"剪枝"来优化它。 理解回溯算法 回溯…...
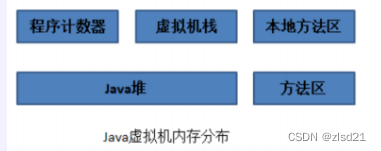
java面试-jvm
JVM JVM 是 java 虚拟机,简单来说就是能执行标准 java 字节码的虚拟计算机 JVM 是如何工作的 首先程序在执行之前先要把 Java 代码(.java)转换成字节码(.class),JVM 通过类加载器(ClassLoade…...
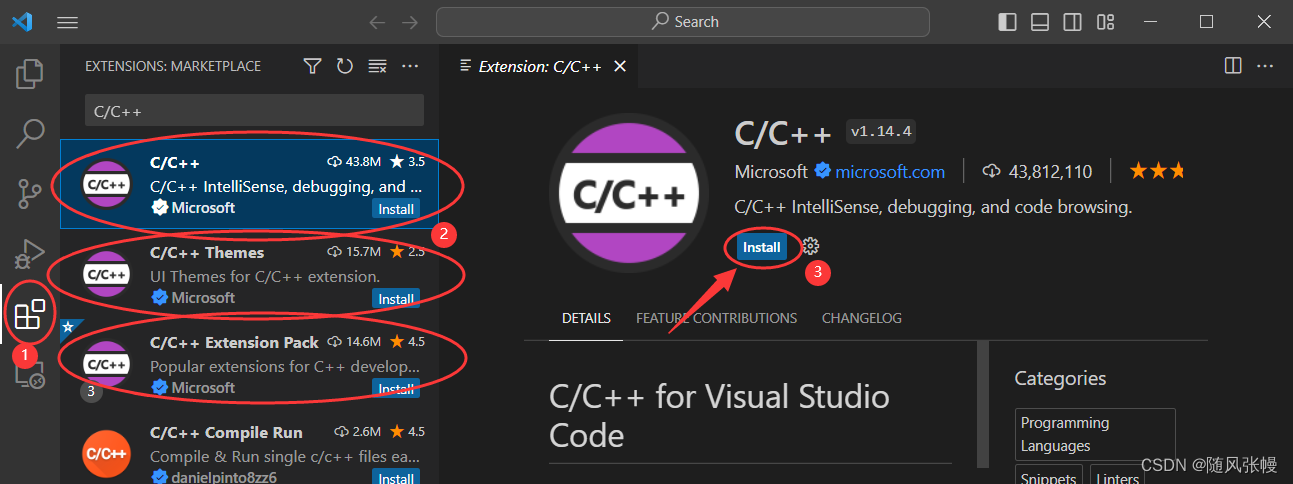
vscode下载与使用
1.vscode下载 官网下载地址:Download Visual Studio Code - Mac, Linux, Windows下载太慢,推荐文章:解决VsCode下载慢问题_vscode下载太慢_迷小圈的博客-CSDN博客下载太慢,推荐下载链接:https://vscode.cdn.azure.cn/s…...

人员摔倒识别预警算法 opencv
人员摔倒识别预警算法通过opencv网络模型技术,人员摔倒识别预警算法能够智能检测现场画面中人员有没有摔倒,无需人为干预可以立刻抓拍告警。OpenCV的全称是Open Source Computer Vision Library,是一个跨平台的计算机视觉处理开源软件库&…...
| 机考必刷)
华为OD机试题 - 火星文计算(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解:火星文计算题目输入输出示例一输入输出说明Code解题思路版权说明…...

AI人工智能 - 初探
1.应用场景 主要用于了解和系统学习AI,从而可以在工作生活中利用AI做一些事。 2.学习/操作 1.文档阅读 下面的内容来自于与chatGPT的对话 2.整理输出 介绍AI 人工智能(Artificial Intelligence,简称AI)是计算机科学中的一个分支&…...

Spring-AOP工作流程
Spring-AOP工作流程 3,AOP工作流程 3.1 AOP工作流程 由于AOP是基于Spring容器管理的bean做的增强,所以整个工作过程需要从Spring加载bean说起: 流程1:Spring容器启动 容器启动就需要去加载bean,哪些类需要被加载呢?需要被增强的类,如:B…...

C51---串口发送指令,控制LED灯亮灭
1.Code: #include "reg52.h" #include "intrins.h" sfr AUXR 0x8E; sbit D5 P3^7; void UartInit(void) //9600bps11.0592MHz { //PCON & 0x7F; //波特率不倍速 AUXR 0x01; SCON 0x50; //8位数据,可变波…...

【Wiki】XWiki数据备份
XWiki为主题使用java开发的开源wiki,官网地址如下: https://www.xwiki.org/xwiki/bin/view/Main/ 目录1、 XWiki升级数据备份1.1、 获取XWiki配置的数据库与持久化目录信息1.2 备份数据库信息1.3 备份持久化目录2、XWiki数据迁移如果一个知识库不能确保数…...

ctk框架开发Qt插件应用示例工程
目录 前言 约定 插件工程pluginApp: 主启动工程StartApp: 效果演示 结语...
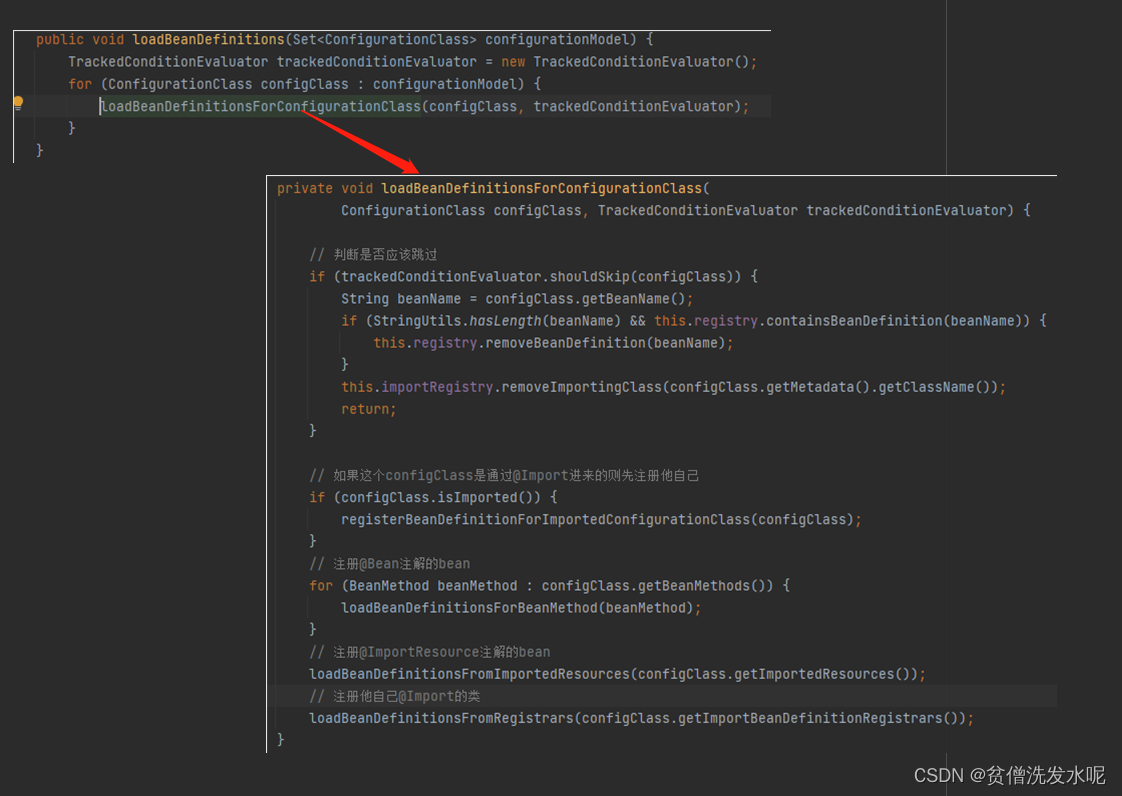
spring5源码篇(4)——beanFactoryPostProcessor执行/注解bean的装配
spring-framework 版本:v5.3.19 前面研究了beanDefinition的注册,但也仅仅是注册这一动作。那么在spring容器启动的过程中,是何时/如何装配的?以及装配的bean是如何注入的? (考虑到xml方式基本不用了以及篇…...

masstransit的message几个高级用法
1)问题,Class MessageA 基类,Class MessageB继承自MessageA; 用bus.Publish方法本想把有些消息只发给B队列,结果由于其继承关系A队列也获得了消息; 解决方法用send, Uri uri new Uri(RabbitM…...

漏洞分析丨cve-2012-0003
作者:黑蛋一、漏洞简介这次漏洞属于堆溢出漏洞,他是MIDI文件中存在的堆溢出漏洞。在IE6,IE7,IE8中都存在这个漏洞。而这个漏洞是Winmm.dll中产生的。二、漏洞环境虚拟机调试工具目标软件辅助工具XP-SP3、KaliOD、IDAIE6Windbg组件gflags.exe三…...

rm命令——删除文件或目录
rm命令是英文单词remove的缩写,主要功能是删除文件或目录。 因为删除文件是一个破坏性动作,因此,在使用时需要格外小心,在执行之前一定要再三确认删除的是哪个目录中的什么文件。 rm命令的语法格式如下: rm [选项] …...

【零基础入门学习Python---Python的基本语法使用】
一.Python基本语法使用 Python是一种易学且功能强大的编程语言,具有简洁的语法和广泛的应用领域。在本文中,我们将介绍Python的基本语法使用,以帮助初学者快速入门Python编程。 1.1 注释 Python 支持两种类型的注释:单行注释和多行注释。 单行注释:以 # 符号开头,从 # …...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...
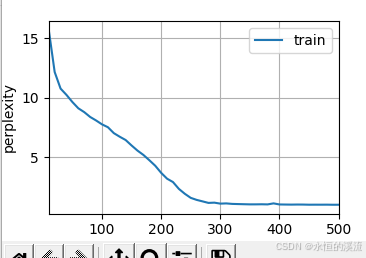
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...

虚幻基础:角色旋转
能帮到你的话,就给个赞吧 😘 文章目录 移动组件使用控制器所需旋转:组件 使用 控制器旋转将旋转朝向运动:组件 使用 移动方向旋转 控制器旋转和移动旋转 缺点移动旋转:必须移动才能旋转,不移动不旋转控制器…...
