当前位置： 首页 > news >正文

汽车行驶中是怎么保障轴瓦安全的？

news 2026/2/8 18:40:19

汽车轴瓦是一种用于减少摩擦和支撑转动部件的关键零部件，通常用于发动机的曲轴、凸轮轴等转动部件上。主要作用是减少转动部件之间的摩擦，支撑和保护曲轴、凸轮轴等旋转部件，确保它们在高速旋转时的稳定性和耐用性。

未标题-3 拷贝-恢复的-恢复的-恢复的-恢复的-恢复的 拷贝.jpg

在汽车轴瓦加工过程中，人工检测员必须敏锐感知，并立即对产品质量作出判断，确保不会将瑕疵品送到消费者手中。然而，生产线速度越快，产品越复杂，缺陷越模糊，人工检测员很难满足生产效率需求。随着技术的发展，在线视觉检测设备被应用到汽车生产制造的各个环节，外观缺陷检测也不例外。

2-2404231004404S 拷贝.jpg

检测案例

检测需求：混料、少料。

检测效果

混料

image.png

定位唇有无

image.png

油槽有无

image.png

五金视觉检测设备及应用技术探讨五金视觉检测设备的最新技术应用,提供各地区设备报价,助力五金行业生产质量提升。icon-default.png?t=N7T8https://www.sipotekccd.com/jinshuwujin/ 

相关文章：

汽车行驶中是怎么保障轴瓦安全的？

汽车轴瓦是一种用于减少摩擦和支撑转动部件的关键零部件，通常用于发动机的曲轴、凸轮轴等转动部件上。主要作用是减少转动部件之间的摩擦，支撑和保护曲轴、凸轮轴等旋转部件，确保它们在高速旋转时的稳定性和耐用性。 在汽车轴瓦加工过程中&am…...

编程日记 2024/6/16 0:51:25

洗地机哪款好？洗地机十大名牌排行榜

随着科技的发展，各种家居清洁工具层出不穷，为我们的生活带来了诸多便利。在众多清洁工具中，洗地机的清洁效果更受大家喜爱，它能够完美解决了扫地机无法做到的干湿垃圾“一遍清洁”效果，而且几乎能解决日常生活中所有的…...

编程日记 2024/6/16 0:50:24

spark mllib 特征学习笔记 （二）

当然，请继续介绍其他特征处理方法的公式、适用场景和案例： 10. StringIndexer 公式： 将字符串类型的标签转换为数值索引： StringIndexer ( x ) { 0 , 1 , 2 , … , N − 1 } \text{StringIndexer}(x) \{0, 1, 2, \ldots, N-1…...

编程日记 2024/6/16 0:47:20

湘潭大学软件工程数据库2（题型，复习资源和计划）

文章目录 选择题关系范式事务分析E-R 图sql作业题答案链接（仅限有官方答案的版本）结语 现在实验全部做完了，实验和作业占比是百分之 40 ，通过上图可以看出来，重点是 sql 语言 所以接下来主要就是学习 sql 语句怎么书写…...

编程日记 2024/6/16 0:45:18

第二十三节:带你梳理Vue2:Vue插槽的认识和基本使用

前言: 通过上一节的学习,我们知道了如何将数据从父组件中传递到子组件中, 除了除了将数据作为props传入到组件中,Vue还允许传入HTML, Vue 实现了一套内容分发的 API&#xff0c;这套 API 的设计灵感源自 Web Components 规范草案&#xff0c;将 <slot> 元素作为承载分发…...

编程日记 2024/6/16 0:44:17

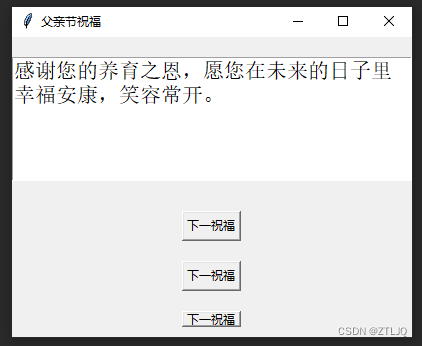
父亲节马上到了-和我一起用Python写父亲节的祝福吧

前言 让我们一起用Python写一段父亲节的祝福吧 &#x1f4dd;个人主页→数据挖掘博主ZTLJQ的主页 个人推荐python学习系列&#xff1a; ☄️爬虫JS逆向系列专栏 - 爬虫逆向教学 ☄️python系列专栏 - 从零开始学python 话不多说先上代码 import tkinter as tk from doctest imp…...

编程日记 2024/6/16 0:43:16

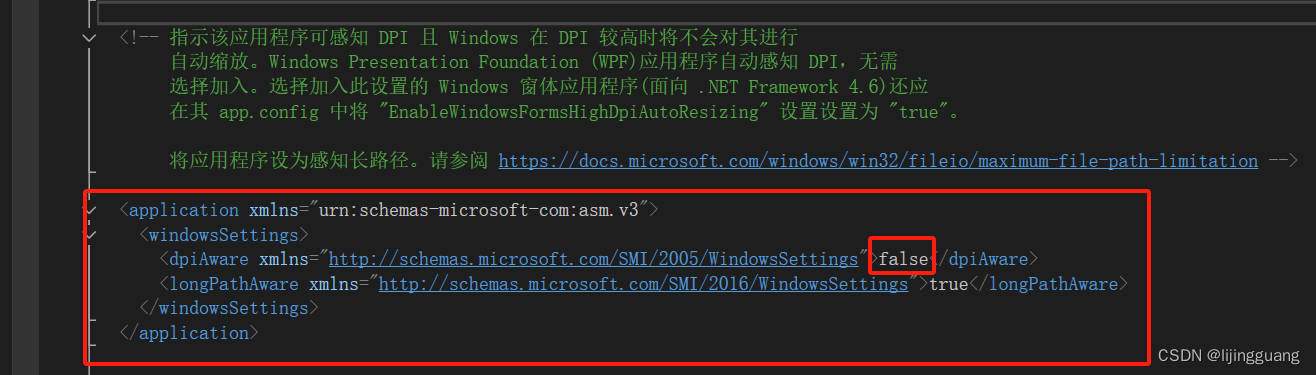
winform 应用程序 添加 wpf控件后影响窗体DPI改变

第一步&#xff1a;添加 应用程序清单文件 app.manifest 第二步&#xff1a;把这段配置 注释放开&#xff0c;第一个配置true 改成false...

编程日记 2024/6/16 0:42:15

Web前端开发素材：探索、选择与应用的艺术

Web前端开发素材&#xff1a;探索、选择与应用的艺术 在Web前端开发的广袤领域中&#xff0c;素材的选择与应用无疑是一项至关重要的技能。它们如同构建网页的砖石&#xff0c;既承载着设计的美感&#xff0c;又影响着用户体验的深度。本文将从四个方面、五个方面、六个方面和…...

编程日记 2024/6/16 0:41:14

LeetCode | 20.有效的括号

这道题就是栈这种数据结构的应用&#xff0c;当我们遇到左括号的时候&#xff0c;比如{,(,[&#xff0c;就压栈&#xff0c;当遇到右括号的时候&#xff0c;比如},),]&#xff0c;就把栈顶元素弹出&#xff0c;如果不匹配&#xff0c;则返回False&#xff0c;当遍历完所有元素后…...

编程日记 2024/6/16 0:40:13

ceph scrub 错误记录

目的 记录 ceph scrub 错误问题解决 ceph scrub 故障故障信息 cluster:id: xxx-xxx-xxxhealth: HEALTH_ERR2 scrub errorsPossible data damage: 2 pg inconsistentmessage 日志信息 # egrep -i medium|i\/o error|sector|Prefailure /var/log/messages Jun 15 00:23:37 m…...

编程日记 2024/6/16 0:39:11

cs与msf权限传递，以及mimikatz抓取明文密码

cs与msf权限传递&#xff0c;以及mimikatz抓取win10明文密码 1、环境准备2、Cobalt Strike ------> MSF2.1 Cobalt Strike拿权限2.2 将CS权限传递给msf 3、MSF ------> Cobalt Strike3.1 msf拿权限3.2 将msf权限传递给CS 4、使用mimikatz抓取明文密码 1、环境准备 攻击&…...

编程日记 2024/6/16 0:38:11

Windows下的zip压缩包版Mysql8.3.0数据迁移到Mysql8.4.0可以用拷贝data文件夹的方式

Windows下的zip压缩包版Mysql8.3.0数据迁移到Mysql8.4.0可以用拷贝data文件夹的方式 拷贝后, 所有账户和数据都是一样的 步骤 停止MySQL服务 net stop mysql 或 sc.exe stop mysql net stop mysqlsc.exe stop mysql卸载 Mysql8.3.0 的服务 mysqld remove 或 mysqld remove m…...

编程日记 2024/6/16 0:37:09

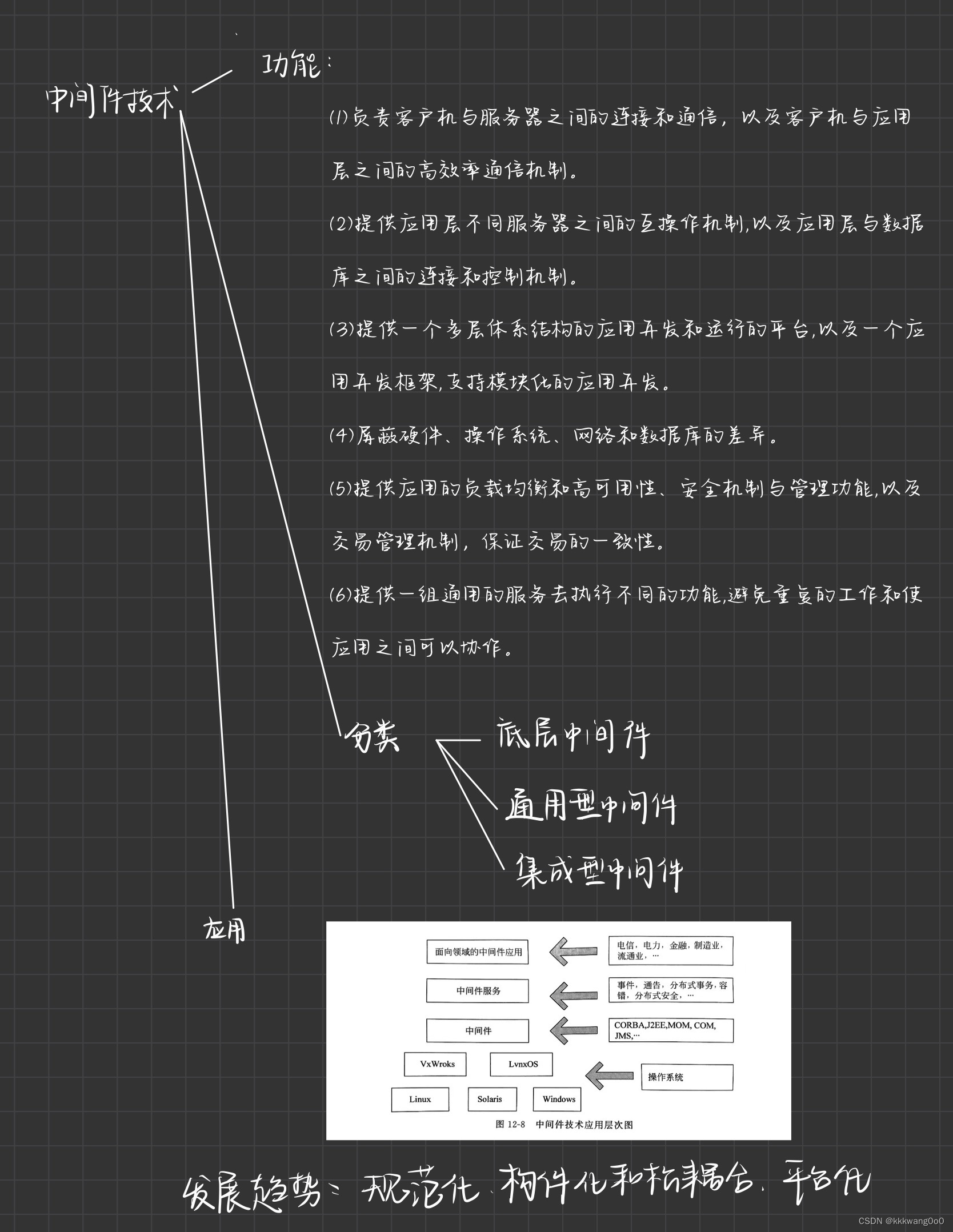
软件体系结构笔记（自用）

来自《软件体系结构原理、方法与实践&#xff08;第三版&#xff09;》清华大学出版社 张友生编著 1-8章12章 复习笔记 如有错误&#xff0c;欢迎指正&#xff01;&#xff01;&#xff01;...

编程日记 2024/6/16 0:35:07

java安装并配置环境

安装前请确保本机没有java的残留&#xff0c;否则将会安装报错 1.安装java jdk&#xff1a;安装路径Java Downloads | Oracle 中国 百度网盘链接&#xff1a;https://pan.baidu.com/s/11-3f2QEquIG3JYw4syklmQ 提取码&#xff1a;518e 2.双击 按照流程直接点击下一步&#x…...

编程日记 2024/6/16 0:34:06

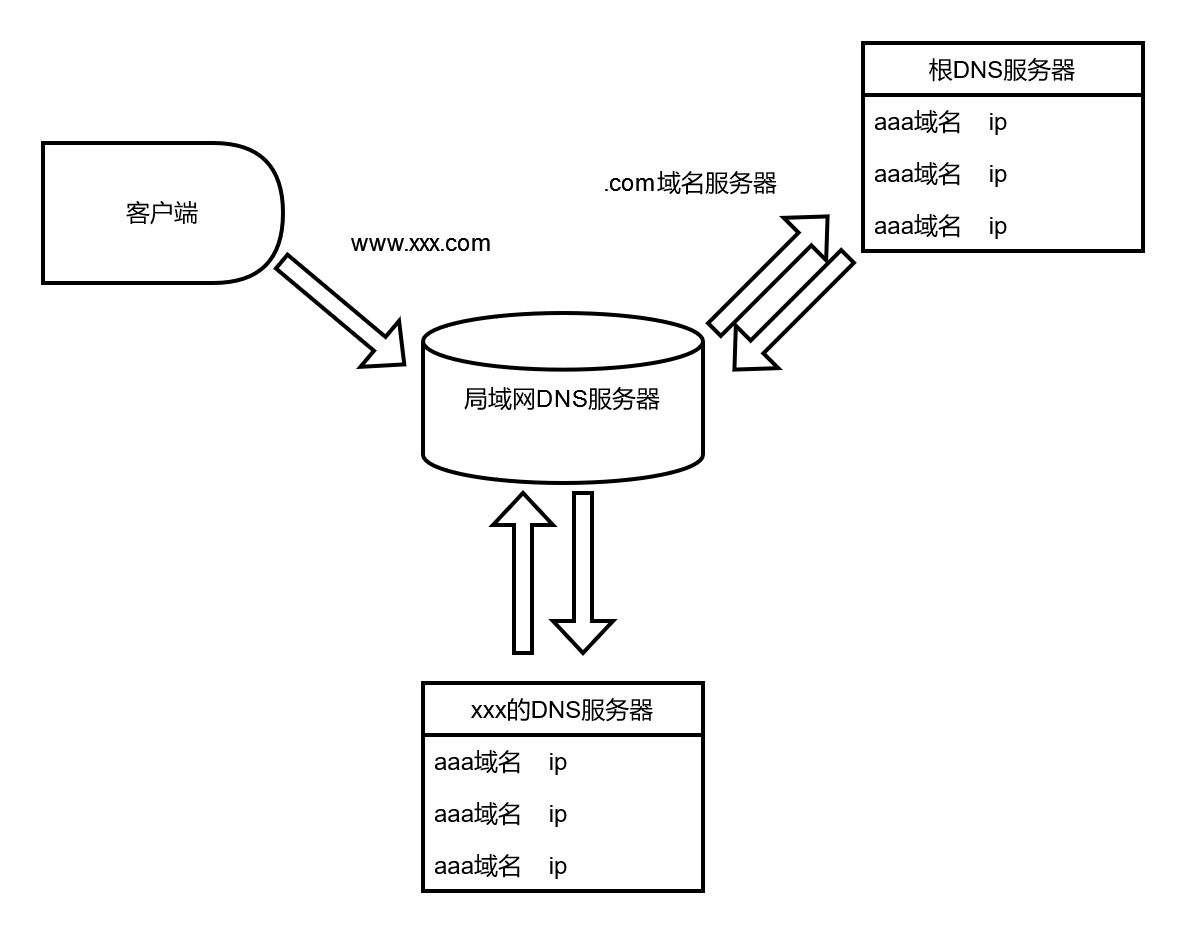
探索互联网寻址机制 | 揭秘互联网技术的核心，解析网络寻址

揭秘互联网技术的核心&#xff0c;解析网络寻址题 前提介绍局域网地址IP地址的分配方式动态IP分配机制内部网&#xff08;intranet&#xff09;ICANN负责IP分配DHCP协议获取IP地址 域名系统域名是什么域名工作方式hosts文件存储域名映射关系DNS分布式数据库DNS域名解析 Java进行…...

编程日记 2024/6/16 0:33:05

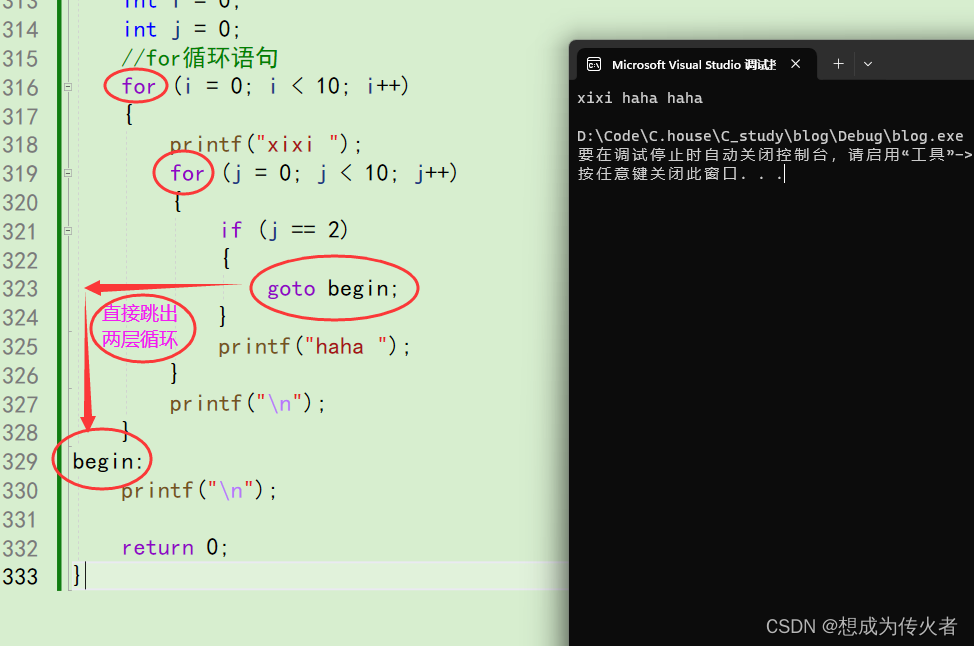
C语言学习笔记之结构篇

C语言是一门结构化程序设计语言。在C语言看来&#xff0c;现实生活中的任何事情都可看作是三大结构或者三大结构的组合的抽象&#xff0c;即顺序&#xff0c;分支&#xff08;选择&#xff09;&#xff0c;循环。 所谓顺序就是一条路走到黑&#xff1b;生活中在很多事情上我们都…...

编程日记 2024/6/16 0:31:02

C++笔记之一个函数多个返回值的方法、std::pair、std::tuple、std::tie的用法

C++笔记之一个函数多个返回值的方法、std::pair、std::tuple、std::tie的用法 —— 2024-06-08 杭州 code review! 文章目录 C++笔记之一个函数多个返回值的方法、std::pair、std::tuple、std::tie的用法一.从一个函数中获取多个返回值的方法1. 使用结构体或类2. 使用`std::t…...

编程日记 2024/6/16 0:30:01

GDB：从零开始入门GDB

目录 1.前言 2.开启项目报错 3.GDB的进入和退出 4.GDB调试中查看代码和切换文件 5.GDB调试中程序的启动和main函数传参 6.GDB中断点相关的操作 7.GDB中的调试输出指令 8.GDB中自动输出值指令 9.GDB中的调试指令 前言 在日常开发中&#xff0c;调试是我们必不可少的技能。在专业…...

编程日记 2024/6/16 0:29:00

服务器权限管理

我们linux服务器上有严格的权限等级&#xff0c;如果权限过高导致误操作会增加服务器的风险。所以对于了解linux系统中的各种权限及要给用户&#xff0c;服务等分配合理的权限十分重要。&#xff08;权限越大&#xff0c;责任越大&#xff09; 1.基本权限 U--user用户,G-group…...

编程日记 2024/6/16 0:27:59

08 SpringBoot 自定定义配置

SpringBoot自定义配置有三种方式&#xff1a; 使用PropertySource进行自定义配置 使用ImportResource进行自定义配置 使用Configuration进行自定义配置 PropertySource ​ 如果将所有的配置都集中到 application.properties 或 application.yml 中&#xff0c;那么这个配置文…...

编程日记 2024/6/16 0:26:58

React 第五十五节 Router 中 useAsyncError的使用详解

前言 useAsyncError 是 React Router v6.4 引入的一个钩子&#xff0c;用于处理异步操作&#xff08;如数据加载&#xff09;中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误&#xff1a;捕获在 loader 或 action 中发生的异步错误替…...

编程新知 2025/11/25 10:36:53

＜6＞-MySQL表的增删查改

目录 一&#xff0c;create&#xff08;创建表&#xff09; 二&#xff0c;retrieve&#xff08;查询表&#xff09; 1&#xff0c;select列 2&#xff0c;where条件 三&#xff0c;update&#xff08;更新表&#xff09; 四&#xff0c;delete&#xff08;删除表&#xf…...

编程新知 2025/12/11 18:28:17

遍历 Map 类型集合的方法汇总

1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

编程新知 2026/1/24 15:08:45

C++ 求圆面积的程序（Program to find area of a circle）

给定半径r&#xff0c;求圆的面积。圆的面积应精确到小数点后5位。 例子&#xff1a; 输入&#xff1a;r 5 输出&#xff1a;78.53982 解释&#xff1a;由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982&#xff0c;因为我们只保留小数点后 5 位数字。 输…...

编程新知 2026/1/31 12:52:15

IT供电系统绝缘监测及故障定位解决方案

随着新能源的快速发展&#xff0c;光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域&#xff0c;IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选&#xff0c;但在长期运行中&#xff0c;例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

编程新知 2026/2/1 6:36:36

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用

1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

编程新知 2025/10/3 17:30:30

网络编程（UDP编程）

思维导图 UDP基础编程&#xff08;单播&#xff09; 1.流程图 服务器&#xff1a;短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

编程新知 2026/2/4 17:31:44

Spring AI与Spring Modulith核心技术解析

Spring AI核心架构解析 Spring AI&#xff08;https://spring.io/projects/spring-ai&#xff09;作为Spring生态中的AI集成框架&#xff0c;其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似&#xff0c;但特别为多语…...

编程新知 2025/12/14 17:38:21

springboot整合VUE之在线教育管理系统简介

可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生&#xff0c;小白用户&#xff0c;想学习知识的 有点基础&#xff0c;想要通过项…...

编程新知 2026/1/26 9:30:45

Go 语言并发编程基础：无缓冲与有缓冲通道

在上一章节中&#xff0c;我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道&#xff0c;它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好&#xff0…...

编程新知 2026/1/29 3:25:02