支持向量机(SVM)中核函数的本质意义
本质上在做什么?
内积是距离度量,核函数相当于将低维空间的距离映射到高维空间的距离,并非对特征直接映射。
为什么要求核函数是对称且Gram矩阵是半正定?
核函数对应某一特征空间的内积,要求①核函数对称;②Gram矩阵半正定。
证明内积对应的Gram矩阵半正定:
α T K α = [ α 1 , α 2 , ⋯ , α n ] [ κ ( x 1 , x 1 ) κ ( x 1 , x 2 ) ⋯ κ ( x 1 , x n ) κ ( x 2 , x 1 ) κ ( x 2 , x 2 ) ⋯ κ ( x 1 , x n ) ⋮ ⋮ ⋱ ⋮ κ ( x n , x 1 ) κ ( x n , x 2 ) ⋯ κ ( x n , x n ) ] [ α 1 α 2 ⋮ α n ] = ∑ i = 1 n ∑ j = 1 n α i κ ( x i , x j ) α j = ∑ i = 1 n ∑ j = 1 n α i α j ⟨ ϕ ( x i ) , ϕ ( x j ) ⟩ = ⟨ ∑ i = 1 n α i ϕ ( x i ) , ∑ j = 1 n α j ϕ ( x j ) ⟩ = ∥ ∑ i = 1 n α i ϕ ( x i ) ∥ 2 2 ⩾ 0 \begin{aligned} {{ \bm \alpha}^{\rm T} {\bm K} { \bm \alpha}} &=\begin{bmatrix} {\alpha}_1, {\alpha}_2, \cdots, {\alpha}_n \end{bmatrix} \begin{bmatrix} \kappa \left( {\bm x}_1, {\bm x}_1 \right) &\kappa \left( {\bm x}_1, {\bm x}_2 \right) &\cdots &\kappa \left( {\bm x}_1, {\bm x}_n \right) \\ \kappa \left( {\bm x}_2, {\bm x}_1 \right) &\kappa \left( {\bm x}_2, {\bm x}_2 \right) &\cdots &\kappa \left( {\bm x}_1, {\bm x}_n \right) \\ \vdots &\vdots &\ddots &\vdots \\ \kappa \left( {\bm x}_n, {\bm x}_1 \right) &\kappa \left( {\bm x}_n, {\bm x}_2 \right) &\cdots &\kappa \left( {\bm x}_n, {\bm x}_n \right) \\ \end{bmatrix} \begin{bmatrix} {\alpha}_1 \\ {\alpha}_2 \\ \vdots \\ {\alpha}_n \\ \end{bmatrix} \\ &= \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} {\alpha}_i \kappa \left( {\bm x}_i, {\bm x}_j \right) {\alpha}_j \\ &= \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} {\alpha}_i {\alpha}_j \langle \phi \left( {\bm x}_i \right), \phi \left( {\bm x}_j \right) \rangle\\ &= \langle \sum\limits_{i=1}^{n} {\alpha}_i \phi \left( {\bm x}_i \right), \sum\limits_{j=1}^{n} {\alpha}_j \phi \left( {\bm x}_j \right) \rangle \\ &= \lVert \sum\limits_{i=1}^{n} {\alpha}_i \phi \left( {\bm x}_i \right) \rVert^2_2 \\ &\geqslant 0 \end{aligned} αTKα=[α1,α2,⋯,αn] κ(x1,x1)κ(x2,x1)⋮κ(xn,x1)κ(x1,x2)κ(x2,x2)⋮κ(xn,x2)⋯⋯⋱⋯κ(x1,xn)κ(x1,xn)⋮κ(xn,xn) α1α2⋮αn =i=1∑nj=1∑nαiκ(xi,xj)αj=i=1∑nj=1∑nαiαj⟨ϕ(xi),ϕ(xj)⟩=⟨i=1∑nαiϕ(xi),j=1∑nαjϕ(xj)⟩=∥i=1∑nαiϕ(xi)∥22⩾0
相关文章:
中核函数的本质意义)
支持向量机(SVM)中核函数的本质意义
本质上在做什么? 内积是距离度量,核函数相当于将低维空间的距离映射到高维空间的距离,并非对特征直接映射。 为什么要求核函数是对称且Gram矩阵是半正定? 核函数对应某一特征空间的内积,要求①核函数对称;②…...
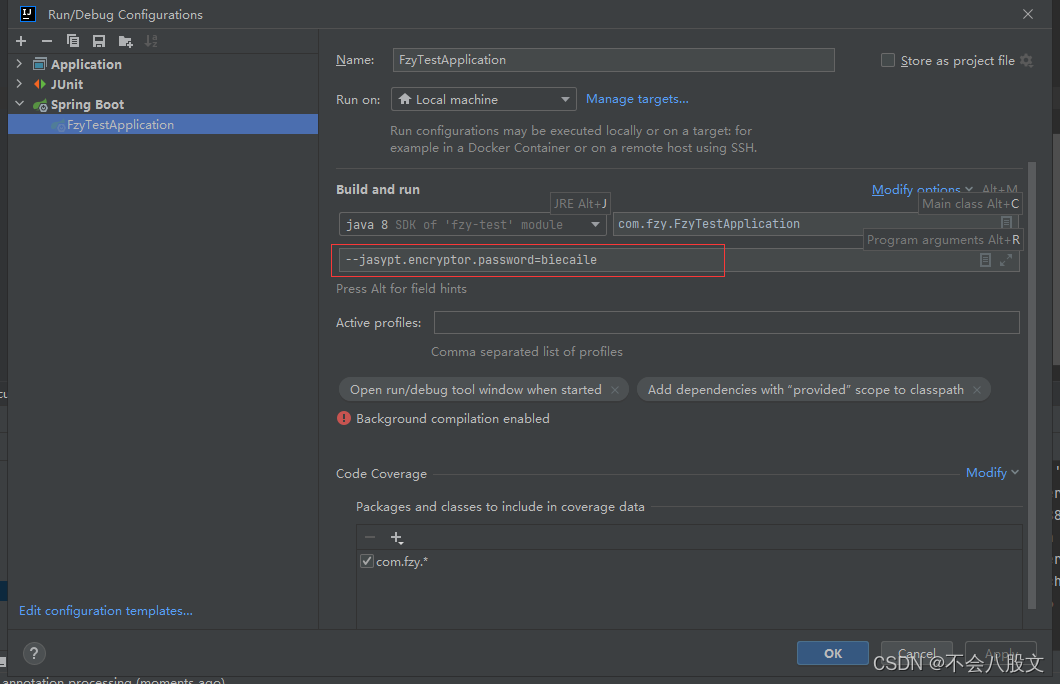
SpringBoot使用jasypt实现数据库信息的脱敏,以此来保护数据库的用户名username和密码password(容易上手,详细)
1.为什么要有这个需求? 一般当我们自己练习的时候,username和password直接是爆露出来的 假如别人路过你旁边时看到了你的数据库账号密码,他跑到他的电脑打开navicat直接就是一顿连接,直接疯狂删除你的数据库,那可就废…...

Python日志配置策略
1 三种情况下都能实现日志打印: 被库 A 调用,使用库 A 的日志配置。被库 B 调用,使用库 B 的日志配置。独立运行,使用自己的日志配置。 需要实现一个灵活的日志配置策略,使得日志记录器可以根据调用者或运行环境自动…...
想学编程,什么语言最好上手?
Python是许多初学者的首选,因为它的语法简洁易懂,而且有丰富的资源和社区支持。我这里有一套编程入门教程,不仅包含了详细的视频 讲解,项目实战。如果你渴望学习编程,不妨点个关注,给个评论222,…...

binlog和redolog有什么区别
在数据库管理系统中,binlog(binary log)和 redolog(redo log)是两种重要的日志机制,它们在数据持久性和故障恢复方面扮演着关键角色。虽然它们都用于记录数据库的变化,但它们的目的和使用方式有…...
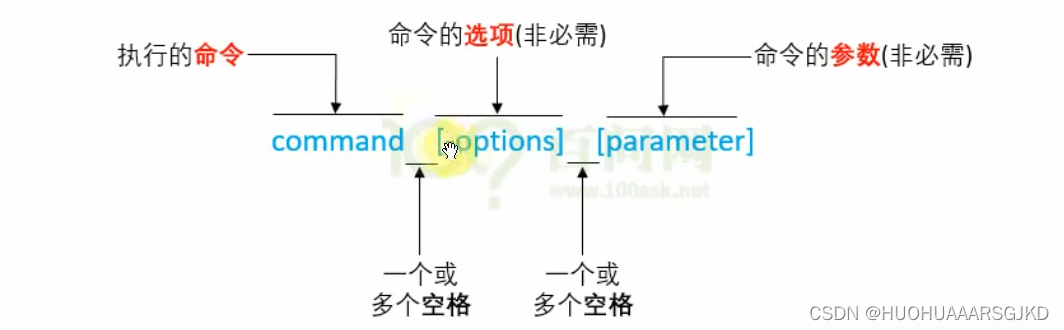
Linux笔记--ubuntu文件目录+命令行介绍
文件目录 命令行介绍 当我们在ubuntu中命令行处理位置输入ls后会显示出其所有目录,那么处理这些命令的程序就是shell,它负责接收用户的输入,并根据输入找到其他程序并运行 命令行格式 linux的命令一般由三部分组成:command命令、…...

71、最长上升子序列II
最长上升子序列II 题目描述 给定一个长度为N的数列,求数值严格单调递增的子序列的长度最长是多少。 输入格式 第一行包含整数N。 第二行包含N个整数,表示完整序列。 输出格式 输出一个整数,表示最大长度。 数据范围 1 ≤ N ≤ 100000…...
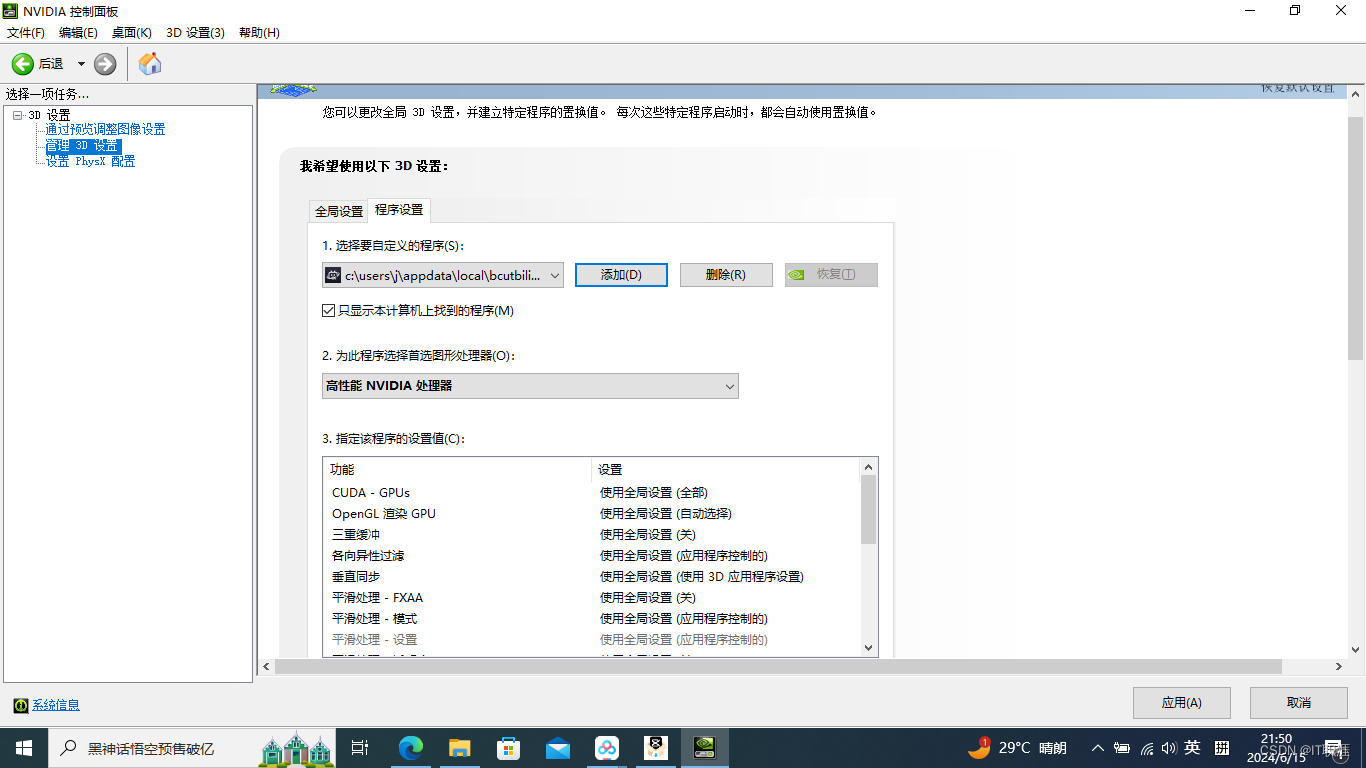
解决必剪电脑版导出视频缺斤少两的办法
背景 前几天将电脑重置了,今天想要剪辑一下视频,于是下载了必剪,将视频、音频都调整好,导出,结果15分钟的视频只能导出很短的时长,调整参数最多也只能导出10分钟,My God! 解决 首…...
)
新人学习笔记之(常量)
一、什么是常量 1.常量:在程序的执行过程中,其值不能发生改变的数据 二、常量的分类 常量类型说明举例整型常量整数、负数、0123 456实型常量所有带小数点的数字1.93 18.2字符常量单引号引起来的字母、数字、英文符号S B字符串常量双引号引起来的&…...

Lua解释器裁剪
本文目录 1、引言2、文件功能3、选择需要初始化的库4、结论 文章对应视频教程: 已更新。见下方 点击图片或链接访问我的B站主页~~~ Lua解释器裁剪,很简单~ 1、引言 在嵌入式中使用lua解释器,很多时候会面临资源紧张的情况。 同时,…...

web前端设计nav:深入探索导航栏设计的艺术与技术
web前端设计nav:深入探索导航栏设计的艺术与技术 在web前端设计中,导航栏(nav)扮演着至关重要的角色,它不仅是用户浏览网站的指引,更是网站整体设计的点睛之笔。本文将从四个方面、五个方面、六个方面和七…...

分析解读NCCL_SHM_Disable与NCCL_P2P_Disable
在NVIDIA的NCCL(NVIDIA Collective Communications Library)库中,NCCL_SHM_Disable 和 NCCL_P2P_Disable 是两个重要的环境变量,它们控制着NCCL在多GPU通信中的行为和使用的通信机制。下面是对这两个环境变量的详细解读࿱…...

使用 Python 进行测试(6)Fake it...
总结 如果我有: # my_life_work.py def transform(param):return param * 2def check(param):return "bad" not in paramdef calculate(param):return len(param)def main(param, option):if option:param transform(param)if not check(param):raise ValueError(…...

Flink Watermark详解
Flink Watermark详解 一、概述 Flink Watermark是Apache Flink框架中为了处理乱序和延迟事件时间数据而引入的一种机制。在流处理中,由于数据可能不是按照事件产生的时间顺序到达的,Watermark被用来告知系统在该时间戳之前的数据已经全部到达ÿ…...

LeetCode538.把二叉搜索树转换为累加树
class Solution { public:int sum 0; TreeNode* convertBST(TreeNode* root) { if (root){convertBST(root->right);sum root->val;root->val sum;convertBST(root->left);}return root;}};...

关于编程思想
面向过程思想 面向过程就是分析出解决问题所需要的步骤,然后用函数把这些步骤一步一步实现,使用的时候再一个一个的依次调用就可以了 JS就是典型的面向过程的编程语言 优点: 性能比面向对象编程高,适合跟硬件联系很紧密的东西…...
521. 最长特殊序列 Ⅰ(Rust单百解法-脑筋急转弯)
题目 给你两个字符串 a 和 b,请返回 这两个字符串中 最长的特殊序列 的长度。如果不存在,则返回 -1 。 「最长特殊序列」 定义如下:该序列为 某字符串独有的最长 子序列 (即不能是其他字符串的子序列) 。 字符串 s …...
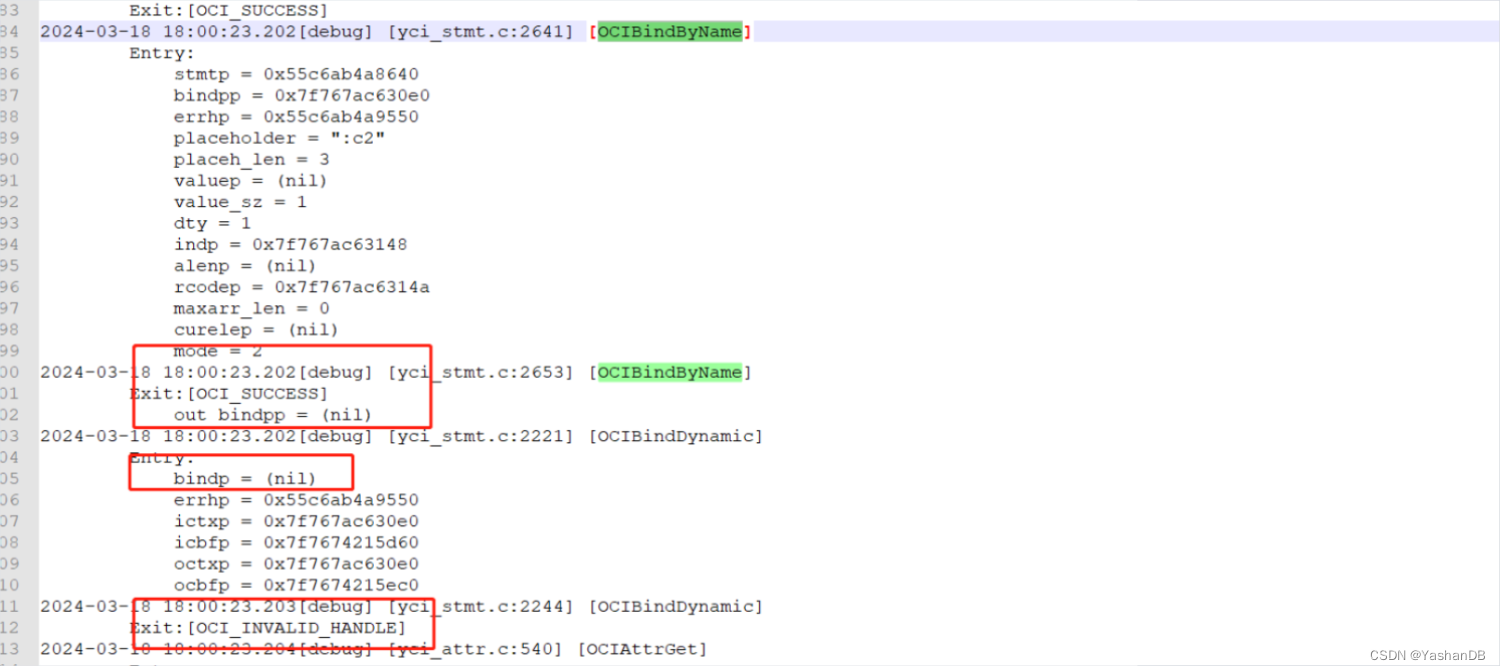
【YashanDB知识库】PHP使用OCI接口使用数据库绑定参数功能异常
【问题分类】驱动使用 【关键字】OCI、驱动使用、PHP 【问题描述】 PHP使用OCI8连接yashan数据库,使用绑定参数获取数据时,出现报错 如果使用PDO_OCI接口连接数据库,未弹出异常,但是无法正确获取数据 【问题原因分析】 开启O…...

深入分析 Android BroadcastReceiver (三)
文章目录 深入分析 Android BroadcastReceiver (三)1. 广播消息的优缺点及使用场景1.1 优点1.2 缺点 2. 广播的使用场景及代码示例2.1. 系统广播示例:监听网络状态变化 2.2. 自定义广播示例:发送自定义广播 2.3. 有序广播示例:有序广播 2.4. …...

在java中使用Reactor 项目中的一个类Mono,用于表示异步单值操作
Mono 是 Reactor 项目中的一个类,用于表示异步单值操作。Reactor 是一个响应式编程库,广泛应用于 Java 中的异步编程和非阻塞 I/O 操作。Mono 可以类比为一个可能(或将来)包含零个或一个值的异步计算结果。与 Flux(另一…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
