第5章:模型预测控制(MPC)的代码实现
1. 建立 QP 模型:
1.1 车辆模型:
注:使用车辆横向动力学模型 + 纵向动力学模型(误差模型)

1.2 QP 问题模型:
注:详细推导见 笔记100:使用 OSQP-Eigen 对 MPC 进行求解的方法与代码-CSDN博客 中对【线性系统 + 线性约束】问题的 QP 问题的构建过程;
- 构建代价函数:

- 构建约束:

注1:其中
注2:其中 ,因为本身车辆模型提供的状态空间方程的状态量 x 就是误差量,对于误差量而言他的目标值就是0;
a
a
a
a
a
2. 代码实现
- 头文件 common.h :定义各种结构体
#include <fstream>
#include <iostream>
#include <string>
#include <lgsvl_msgs/VehicleControlData.h>
#include <nav_msgs/Odometry.h>
#include <std_msgs/Header.h>
#include <sensor_msgs/Imu.h>
#include "map.h"
#include "reference_line.h"
#include "ros/ros.h"
#include "tf/tf.h"// 车辆状态信息
struct VehicleState {double x; // 车辆在【全局坐标系】中的 -- x值double y; // 车辆在【全局坐标系】中的 -- y值double heading; // 车辆在【全局坐标系】中的 -- 车辆朝向(车辆横摆角/航向角,也即车辆欧拉角中的偏航角 yaw)double kappa; // 车辆在【全局坐标系】中的 -- 曲率(转弯半径的倒数)double velocity; // 车辆在【全局坐标系】中的 -- 线速度double angular_velocity; // 车辆在【全局坐标系】中的 -- 角速度(横摆角变化率)double acceleration; // 车辆在【全局坐标系】中的 -- 加速度double vx; // 速度在【车身坐标系的x轴】上的分量double vy; // 速度在【车身坐标系的y轴】上的分量double vz; // 速度在【车身坐标系的z轴】上的分量double pitch; // 欧拉角 -- 在【车身坐标系】绕x轴转角 -- 俯仰角double yaw; // 欧拉角 -- 在【车身坐标系】绕y轴转角 -- 偏航角double roll; // 欧拉角 -- 在【车身坐标系】绕z轴转角 -- 横滚角double target_curv; // 期望点的曲率// 起点处车辆的信息double planning_init_x; // 车辆起点在【全局坐标系】中的 -- x值double planning_init_y; // 车辆起点在【全局坐标系】中的 -- y值// addeddouble start_point_x;double start_point_y;double relative_x = 0;double relative_y = 0;double relative_distance = 0;double last_velocity = 0; // 上一个时间步的 -- 车辆线速度double last_v_err = 0; // 上一个时间步的 -- 车辆线速度误差double last_v_time = 0; // 上一个时间步的 -- 速度时间戳double last_acc = 0; // 上一个时间步的 -- 加速度double cur_v_err = 0; // 当前时间步的 -- 速度误差double cur_v_time = 0; // 当前时间步的 -- 速度时间戳double cur_acc = 0; // 当前时间步的 -- 加速度
};// 轨迹(目标)点
struct TrajectoryPoint {double x; // 目标点在【全局坐标系】中的 -- x值double y; // 目标点在【全局坐标系】中的 -- y值double heading; // 目标点在【全局坐标系】中的 -- 目标点处的切线与全局坐标系的x轴之间的夹角(目标航向角)double kappa; // 目标点在【全局坐标系】中的 -- 目标点处的曲率double v; // 目标点在【全局坐标系】中变化的 -- 速度double a; // 目标点在【全局坐标系】中变化的 -- 加速度
};// 目标轨迹(vector容器中装有所有的路径点)
struct TrajectoryData {std::vector<TrajectoryPoint> trajectory_points;
};// 车辆横向动力学模型(误差型)中状态量x包含的4个分量
struct LateralControlError {double lateral_error; // 横向误差double heading_error; // 航向误差double lateral_error_rate; // 横向误差变化率double heading_error_rate; // 航向误差变化率
};// 控制命令
struct ControlCmd {double steer_target; //横向控制命令:方向盘转角double acc; //总想控制命令:油门开度
};typedef std::shared_ptr<LateralControlError> LateralControlErrorPtr;- 头文件 mpc_controller.h :定义车辆模型涉及到的所有矩阵和信息
#pragma once
#include <math.h>
#include <fstream>
#include <iomanip>
#include <memory>
#include <string>
#include "Eigen/Core"
#include "common.h"
#include "mpc_osqp.h"
namespace shenlan {
namespace control {
using Matrix = Eigen::MatrixXd;class MPCController {
public:MPCController();~MPCController();void LoadControlConf();void Init();bool ComputeControlCommand(const VehicleState &localization, const TrajectoryData &planning_published_trajectory, ControlCmd &cmd);protected:double Wheel2SteerPct(const double wheel_angle);void UpdateState(const VehicleState &vehicle_state);void UpdateMatrix(const VehicleState &vehicle_state);// 计算横向误差(未定义)void ComputeLateralErrors(const double x, const double y, const double theta, const double linear_v, const double angular_v, const double linear_a, LateralControlErrorPtr &lat_con_err);// 计算纵向误差(未定义)void ComputeLongitudinalErrors(const VehicleState &vehicle_state);void ComputeErrors(const double x, const double y, const double theta, const double linear_v, const double angular_v, const double linear_a, LateralControlErrorPtr &lat_con_err);void ToTrajectoryFrame(const double x, const double y, const double theta, const double v, const TrajectoryPoint &ref_point, double *ptr_s, double *ptr_s_dot, double *ptr_d, double *ptr_d_dot);TrajectoryPoint QueryNearestPointByPosition(const double x, const double y);// 全局规划路径中的所有点:std::vector<TrajectoryPoint> trajectory_points_;// 车辆的物理参数汇总:double ts_ = 0.0; // 两个控制命令之间的时间间隔double cf_ = 0.0; // 前轮侧偏刚度double cr_ = 0.0; // 后轮侧偏刚度double wheelbase_ = 0.0; // 车辆纵轴长度double mass_ = 0.0; // 车辆总质量double lf_ = 0.0; // 车辆纵轴中的lfdouble lr_ = 0.0; // 车辆纵轴中的lrdouble iz_ = 0.0; // 汽车的转动惯量double steer_ratio_ = 0.0; // 方向盘的转角到轮胎转动角度之间的比值系数Eigen::MatrixXd matrix_a_;Eigen::MatrixXd matrix_a_coeff_;Eigen::MatrixXd matrix_ad_;Eigen::MatrixXd matrix_b_;Eigen::MatrixXd matrix_bd_;Eigen::MatrixXd matrix_state_;Eigen::MatrixXd matrix_r_;Eigen::MatrixXd matrix_q_;Eigen::MatrixXd matrix_q_updated_;const int basic_state_size_ = 6; // 状态量x的大小(横向误差 / 横向误差变化率 / 航向误差 / 航向误差变化率 / 纵向位置误差 / 纵向速度误差)const int controls_ = 2; // 控制量u的大小(方向盘转角 / 汽车加速度)double station_error_ = 0.0; // 纵向位置误差double speed_error_ = 0.0; // 纵向速度误差int mpc_max_iteration_ = 0; // MPC求解器的参数 -- QP求解器最大迭代次数double mpc_eps_ = 0.0; // MPC求解器的参数 -- 计算阈值const int horizon_ = 10; // MPC有限时域长度double max_acceleration_ = 0.0; // 车辆最大加速度double max_deceleration_ = 0.0; // 车辆最小加速度double max_lat_acc_ = 0.0; // 转向时的最大横向加速度double minimum_speed_protection_ = 0.1; // 车辆最小速度double steer_single_direction_max_degree_ = 0.0; // 方向盘的最大转角double wheel_single_direction_max_degree_ = 0.0; // 车轮的最大转角
};} // namespace control
} // namespace shenlan- 源文件 mpc_controller.cpp :
#include "mpc_controller.h"
#include <algorithm>
#include <iomanip>
#include <utility>
#include <vector>
#include "Eigen/LU"
#include "math.h"
using namespace std;
namespace shenlan {
namespace control {// 函数作用:构造函数
MPCController::MPCController() {}
// 函数作用:析构函数
MPCController::~MPCController() {}// 函数作用:初始化车辆物理参数
void MPCController::LoadControlConf() {ts_ = 0.01; // 两个控制命令之间的时间间隔cf_ = 155493.663; // 前轮侧偏刚度cr_ = 155493.663; // 后轮侧偏刚度wheelbase_ = 1.0; // 车辆纵轴长度max_acceleration_ = 0.8; // 车辆最大加速度 (总加速度)max_deceleration_ = -0.8; // 车辆最小加速度 (总加速度)max_lat_acc_ = 5.0; // 转向时的最大横向加速度 (横向加速度)steer_ratio_ = 1.0; // 传动比steer_single_direction_max_degree_ = 40.0; // 方向盘的最大转角(角度)wheel_single_direction_max_degree_ = steer_single_direction_max_degree_ / steer_ratio_ / 180 * M_PI; // 车轮最大转角(弧度)const double mass_fl = 55.0; // 左前悬的质量const double mass_fr = 55.0; // 右前悬的质量const double mass_rl = 65.0; // 左后悬的质量const double mass_rr = 65.0; // 右后悬的质量const double mass_front = mass_fl + mass_fr; // 前悬质量const double mass_rear = mass_rl + mass_rr; // 后悬质量mass_ = mass_front + mass_rear; // 总车质量lf_ = wheelbase_ * (1.0 - mass_front / mass_); // 汽车前轮到中心点的距离lr_ = wheelbase_ * (1.0 - mass_rear / mass_); // 汽车后轮到中心点的距离iz_ = lf_ * lf_ * mass_front + lr_ * lr_ * mass_rear; // 汽车的转动惯量mpc_eps_ = 0.01; // MPC求解器的参数 -- 计算阈值mpc_max_iteration_ = 1500; // MPC求解器的参数 -- 最大迭代次数return;
}// 函数作用:初始化 -- 横向动力学模型中的矩阵 + 代价函数J中的矩阵
void MPCController::Init() {LoadControlConf();// 初始化(连续型)车辆横向动力学模型 -- 矩阵Amatrix_a_ = Matrix::Zero(basic_state_size_, basic_state_size_);matrix_a_(0, 1) = 1.0;matrix_a_(1, 2) = (cf_ + cr_) / mass_;matrix_a_(2, 3) = 1.0;matrix_a_(3, 2) = (lf_ * cf_ - lr_ * cr_) / iz_;matrix_a_(4, 5) = 1;matrix_a_(5, 5) = 0.0;matrix_a_coeff_ = Matrix::Zero(basic_state_size_, basic_state_size_);matrix_a_coeff_(1, 1) = -(cf_ + cr_) / mass_;matrix_a_coeff_(1, 3) = (lr_ * cr_ - lf_ * cf_) / mass_;matrix_a_coeff_(2, 3) = 1.0;matrix_a_coeff_(3, 1) = (lr_ * cr_ - lf_ * cf_) / iz_;matrix_a_coeff_(3, 3) = -1.0 * (lf_ * lf_ * cf_ + lr_ * lr_ * cr_) / iz_;// 初始化(连续型)车辆横向动力学模型 -- 矩阵Bmatrix_b_ = Matrix::Zero(basic_state_size_, controls_);matrix_b_(1, 0) = cf_ / mass_;matrix_b_(3, 0) = lf_ * cf_ / iz_;matrix_b_(4, 1) = 0.0;matrix_b_(5, 1) = -1.0;// 初始化(离散型)车辆横向动力学模型 -- 矩阵Admatrix_ad_ = Matrix::Zero(basic_state_size_, basic_state_size_);// 初始化(离散型)车辆横向动力学模型 -- 矩阵Bdmatrix_bd_ = Matrix::Zero(basic_state_size_, controls_);matrix_bd_ = matrix_b_ * ts_;// 初始化(离散型)车辆横向动力学方程 -- 状态量xmatrix_state_ = Matrix::Zero(basic_state_size_, 1);// 初始化代价函数J -- 矩阵Rmatrix_r_ = Matrix::Identity(controls_, controls_);matrix_r_(0, 0) = 3.25; // 方向盘转角matrix_r_(1, 1) = 1.0; // 车辆加速度(总价速度)// 初始化代价函数J -- 矩阵Qmatrix_q_ = Matrix::Zero(basic_state_size_, basic_state_size_);matrix_q_(0, 0) = 3.0; // 横向误差matrix_q_(1, 1) = 0.0; // 横向误差变化率matrix_q_(2, 2) = 15.0; // 朝向误差matrix_q_(3, 3) = 0.0; // 朝向误差变化率matrix_q_(4, 4) = 0.0; // 纵向位置误差matrix_q_(5, 5) = 10; // 纵向速度误差return;
}// 函数作用:计算目标点和车辆当前位置之间距离的平方
double PointDistanceSquare(const TrajectoryPoint &point, const double x, const double y) {const double dx = point.x - x;const double dy = point.y - y;return dx * dx + dy * dy;
}// 函数作用:将弧度值归化到 [-M_PI, M_PI] 之间,防止弧度值超过量纲
double NormalizeAngle(const double angle) {double a = std::fmod(angle + M_PI, 2.0 * M_PI);if (a < 0.0) a += (2.0 * M_PI);return a - M_PI;
}// 函数作用:
double MPCController::Wheel2SteerPct(const double wheel_angle) {return wheel_angle / wheel_single_direction_max_degree_ * 100;
}// 函数作用:计算控制命令
bool MPCController::ComputeControlCommand(const VehicleState &localization, const TrajectoryData &planning_published_trajectory, ControlCmd &cmd) {// 所有轨迹点(全局规划器提供的全局路径)trajectory_points_ = planning_published_trajectory.trajectory_points;// 更新当前时间步的状态空间变量 x_0(均为误差量)UpdateState(localization);// 更新状态矩阵 Ad// 解释:因为矩阵Ad的计算涉及到车速vx,所以每往后走一个时间步,都要同步更新一下系统横向动力学模型中的Ad矩阵UpdateMatrix(localization);// 初始化控制量u的矩阵Matrix control_matrix = Matrix::Zero(controls_, 1);// 车辆当前的目标状态量 x_ref(也都是误差量,恒定为 0 向量)Matrix reference_state = Matrix::Zero(basic_state_size_, 1);// 初始化控制量u中每个分量的上下限值// 方向盘转角,车辆加速度Matrix lower_bound(controls_, 1);Matrix upper_bound(controls_, 1);lower_bound << -M_PI/6, max_deceleration_;upper_bound << M_PI/6, max_acceleration_;// 初始化状态量x中每个分量的上下限值// 横向误差,横向误差变化率,航向误差,航向误差变化率,纵向位置误差,纵向速度误差Matrix lower_state_bound(basic_state_size_, 1);Matrix upper_state_bound(basic_state_size_, 1);const double max = std::numeric_limits<double>::max();lower_state_bound << -1.0 * max, -1.0 * max, -1.0 * M_PI, -1.0 * max, -1.0 * max, -1.0 * max;upper_state_bound << max, max, M_PI, max, max, max;// 初始化需要发送给carla模拟器的控制命令// 方向盘转角,车辆加速度std::vector<double> control_cmd(controls_, 0);// 初始化QP求解器MpcOsqp mpc_osqp(matrix_ad_, // Admatrix_bd_, // Bdmatrix_q_, // Qmatrix_r_, // Rmatrix_state_, // x0lower_bound, // 不等式约束upper_bound, // 不等式约束lower_state_bound, // 不等式约束upper_state_bound, // 不等式约束reference_state, // 车辆当前位置匹配的目标点的 -- 目标状态量 xrefmpc_max_iteration_, // QP求解器最大迭代次数horizon_, // 有限时域长度mpc_eps_); // 计算阈值// 调用QP求解器开始计算具体的控制命令if (!mpc_osqp.Solve(&control_cmd)) {std::cout << "MPC OSQP solver failed" << std::endl;}else {std::cout << "MPC OSQP problem solved" << std::endl;control_matrix(0, 0) = control_cmd.at(0);control_matrix(1, 0) = control_cmd.at(1);}// 发布控制命令double steer_angle_feedback = control_matrix(0, 0);double acc_feedback = control_matrix(1, 0);cmd.steer_target = steer_angle_feedback;cmd.acc = acc_feedback;return true;
}// 函数作用:更新状态空间变量x
void MPCController::UpdateState(const VehicleState &vehicle_state) {// 智能指针std::shared_ptr<LateralControlError> lat_con_err = std::make_shared<LateralControlError>();// 计算状态量x中的每个分量(存储在变量 lat_con_err 中)ComputeErrors(vehicle_state.x, vehicle_state.y, vehicle_state.heading, vehicle_state.velocity, vehicle_state.angular_velocity, vehicle_state.acceleration, lat_con_err);// 更新状态量x中的每个分量matrix_state_(0, 0) = lat_con_err->lateral_error; // 横向误差matrix_state_(1, 0) = lat_con_err->lateral_error_rate; // 横向误差变化率matrix_state_(2, 0) = lat_con_err->heading_error; // 朝向误差matrix_state_(3, 0) = lat_con_err->heading_error_rate; // 朝向误差变化率matrix_state_(4, 0) = station_error_; // 纵向位置误差matrix_state_(5, 0) = speed_error_; // 纵向速度误差
}// 函数作用:更新矩阵 A_d (计算车辆横向动力学模型 -- 矩阵A + 矩阵Ad)
void MPCController::UpdateMatrix(const VehicleState &vehicle_state) {// 防止车辆速度为0double v;v = std::max(vehicle_state.velocity, minimum_speed_protection_);// 计算(连续型)车辆横向动力学模型 -- 矩阵Amatrix_a_(1, 1) = matrix_a_coeff_(1, 1) / v;matrix_a_(1, 3) = matrix_a_coeff_(1, 3) / v;matrix_a_(3, 1) = matrix_a_coeff_(3, 1) / v;matrix_a_(3, 3) = matrix_a_coeff_(3, 3) / v;// 计算(离散型)车辆横向动力学模型 -- 矩阵AdMatrix matrix_i = Matrix::Identity(matrix_a_.cols(), matrix_a_.cols());matrix_ad_ = (matrix_i - ts_ * 0.5 * matrix_a_).inverse() * (matrix_i + ts_ * 0.5 * matrix_a_);
}// 函数作用:计算状态空间变量x的每个分量
void MPCController::ComputeErrors(const double x, const double y, const double theta, const double linear_v, const double angular_v, const double linear_a, LateralControlErrorPtr& lat_con_err) {// 查询距离车辆当前位置最近的路径点作为目标点TrajectoryPoint target_point;target_point = QueryNearestPointByPosition(x, y);const double dx = x - target_point.x;const double dy = y - target_point.y;const double cos_target_heading = std::cos(target_point.heading);const double sin_target_heading = std::sin(target_point.heading);double lateral_error = cos_target_heading * dy - sin_target_heading * dx; // 横向误差(使用的是车身坐标系和全局坐标系的变换公式计算的)double heading_error = NormalizeAngle(theta - target_point.heading); // 航向误差auto lateral_error_dot = linear_v * std::sin(heading_error); // 横向误差变化率double ref_heading_rate = target_point.kappa * target_point.v; // 航向误差变化率station_error_ = -(dx * cos_target_heading + dy * sin_target_heading); // 纵向位置误差speed_error_ = target_point.v - linear_v * std::cos(abs(heading_error)) / (1 - target_point.kappa * lateral_error); // 纵向速度误差lat_con_err->lateral_error = lateral_error;lat_con_err->heading_error = heading_error;lat_con_err->lateral_error_rate = lateral_error_dot;lat_con_err->heading_error_rate = angular_v - ref_heading_rate;
}// 函数作用:返回全局规划路径上,距离车辆当前位置最近的点
TrajectoryPoint MPCController::QueryNearestPointByPosition(const double x, const double y) {double d_min = PointDistanceSquare(trajectory_points_.front(), x, y);size_t index_min = 0;for (size_t i = 1; i < trajectory_points_.size(); ++i) {double d_temp = PointDistanceSquare(trajectory_points_[i], x, y);if (d_temp < d_min) {d_min = d_temp;index_min = i;}}return trajectory_points_[index_min];
}} // namespace control
} // namespace shenlan- 头文件 mpc_osqp.h :定义 QP 问题所涉及的所有矩阵和信息
#pragma once
#include <algorithm>
#include <limits>
#include <memory>
#include <utility>
#include <vector>
#include "Eigen/Eigen"
#include "osqp/osqp.h"
namespace shenlan {
namespace control {class MpcOsqp {
public:/*** @brief Solver for discrete-time model predictive control problem.* @param matrix_a The system dynamic matrix* @param matrix_b The control matrix* @param matrix_q The cost matrix for control state costfunction* @param matrix_lower The lower bound control constrain matrix* @param matrix_upper The upper bound control constrain matrix * @param matrix_initial_state The initial state matrix* @param max_iter The maximum iterations*/MpcOsqp(const Eigen::MatrixXd &matrix_a, const Eigen::MatrixXd &matrix_b, // Ad, Bdconst Eigen::MatrixXd &matrix_q, const Eigen::MatrixXd &matrix_r, // Q , Rconst Eigen::MatrixXd &matrix_initial_x, // 初始状态空间const Eigen::MatrixXd &matrix_u_lower, // 控制变量下界const Eigen::MatrixXd &matrix_u_upper, // 控制变量上界const Eigen::MatrixXd &matrix_x_lower, // 状态变量下界const Eigen::MatrixXd &matrix_x_upper, // 状态变量上界const Eigen::MatrixXd &matrix_x_ref, // 车辆当前位置匹配的目标点的 -- 目标状态量xconst int max_iter, // QP 求解器的最大迭代次数const int horizon, // MPC 的有限时域长度const double eps_abs); // QP 求解器的计算阈值bool Solve(std::vector<double> *control_cmd);private:void CalculateKernel(std::vector<c_float> *P_data, std::vector<c_int> *P_indices, std::vector<c_int> *P_indptr); // 求 Pvoid CalculateEqualityConstraint(std::vector<c_float> *A_data, std::vector<c_int> *A_indices, std::vector<c_int> *A_indptr); // 求 A_cvoid CalculateGradient(); // 求 qvoid CalculateConstraintVectors(); // 求 l 和 uOSQPSettings* Settings();OSQPData* Data();void FreeData(OSQPData *data);template <typename T>T *CopyData(const std::vector<T> &vec) {T* data = new T[vec.size()];memcpy(data, vec.data(), sizeof(T) * vec.size());return data;}private:Eigen::MatrixXd matrix_a_; // AdEigen::MatrixXd matrix_b_; // BdEigen::MatrixXd matrix_q_; // QEigen::MatrixXd matrix_r_; // REigen::MatrixXd matrix_initial_x_; // x_0const Eigen::MatrixXd matrix_u_lower_; //const Eigen::MatrixXd matrix_u_upper_; //const Eigen::MatrixXd matrix_x_lower_; //const Eigen::MatrixXd matrix_x_upper_; //const Eigen::MatrixXd matrix_x_ref_; // x_refsize_t state_dim_;size_t control_dim_;size_t num_param_;int num_constraint_;int max_iteration_;size_t horizon_;double eps_abs_;Eigen::VectorXd gradient_; // q 矩阵Eigen::VectorXd lowerBound_; // l 向量Eigen::VectorXd upperBound_; // u 向量// 注:没有定义矩阵 P 和 A_c ,因为这俩都是稀疏矩阵,而且很大,如果直接存储太消耗资源,所以使用列压缩的方式转化为了3个特征数组
};} // namespace control
} // namespace shenlan- 源文件 mpc_osqp.cpp :
#include "mpc_osqp.h"
namespace shenlan {
namespace control {// 函数作用:有参构造函数
MpcOsqp::MpcOsqp(const Eigen::MatrixXd &matrix_a, // Adconst Eigen::MatrixXd &matrix_b, // Bdconst Eigen::MatrixXd &matrix_q, // Qconst Eigen::MatrixXd &matrix_r, // Rconst Eigen::MatrixXd &matrix_initial_x, // x_0(当前时间步系统初始状态量)const Eigen::MatrixXd &matrix_u_lower, // 控制量u的下界(维数:2 -- 横向1个 + 纵向1个)const Eigen::MatrixXd &matrix_u_upper, // 控制量u的上界const Eigen::MatrixXd &matrix_x_lower, // 状态量x的下界(维数:6 -- 横向4个 + 纵向2个)const Eigen::MatrixXd &matrix_x_upper, // 状态量x的上界const Eigen::MatrixXd &matrix_x_ref, // x_ref(当前时间步目标状态量,恒定为 0)const int max_iter, // QP 求解器的最大迭代次数const int horizon, // MPC 的有限时域长度const double eps_abs) // QP 求解器的计算阈值: matrix_a_(matrix_a), // 6 * 6 非定值matrix_b_(matrix_b), // 6 * 2 定值matrix_q_(matrix_q), // 6 * 6 定值matrix_r_(matrix_r), // 2 * 2 定值matrix_initial_x_(matrix_initial_x), // 6 * 1 非定值matrix_u_lower_(matrix_u_lower), // 2 * 1 定值matrix_u_upper_(matrix_u_upper), // 2 * 1 定值matrix_x_lower_(matrix_x_lower), // 6 * 1 定值matrix_x_upper_(matrix_x_upper), // 6 * 1 定值matrix_x_ref_(matrix_x_ref), // 6 * 1 定值(恒定为0)max_iteration_(max_iter), horizon_(horizon),eps_abs_(eps_abs) {state_dim_ = matrix_b.rows(); // 状态量数目:6control_dim_ = matrix_b.cols(); // 控制量数目:2num_param_ = state_dim_ * (horizon_ + 1) + control_dim_ * horizon_; // 代价函数涉及参数数目:6 * (10 + 1) + 2 * 10
}// 函数作用:计算 P 矩阵,并将稀疏矩阵 P 表示为 csc_matrix(压缩列存储)格式
void MpcOsqp::CalculateKernel(std::vector<c_float> *P_data, std::vector<c_int> *P_indices, std::vector<c_int> *P_indptr) {// P_data 稀疏矩阵 P 内的所有非零数值// P_indices 稀疏矩阵 P 内每一列上的非零数字的行索引值// P_indptr 稀疏矩阵 P 内截止到到当前列(不含当前列)所有非零数字的数量// 注意:这三个数组是将稀疏矩阵 P 的内容提炼了出来,将这三个数组传入,就知道他们原本代表的稀疏矩阵 P 的样子了// 注意:这三个数组均为函数 csc_matrix() 的参数,函数的作用是通过传入的三个数组,恢复稀疏矩阵 P 原有的样子// 初始化数组 columns// 这个数组没什么特别的含义,只是一个中间量,是为了后面求解数组 P_data / P_indices / P_indptr 更方便// 这个数组用来按列存放稀疏矩阵 P 中每个非零元素,从左到右按顺序遍历稀疏矩阵 P 的每一列,一次寻找一列内的所有非零元素,存放内容为 pair(非零元素所在行索引 , 非零元素值)std::vector<std::vector<std::pair<c_int, c_float>>> columns;// 外侧数组 -- 外壳// 内侧数组 -- 代表按列columns.resize(num_param_);// 临时变量// 作用:用来计数到目前为止遍历到的稀疏矩阵 P 中非零元素的个数int value_index = 0;// 数组 columns 中 -- 稀疏矩阵 P 的左上角对角阵 diag(Q , Q , ... , Q) 对应的部分(N + 1个Q)(N = horizon_)for (size_t i = 0; i <= horizon_; ++i) { // 按 Q 块for (size_t j = 0; j < state_dim_; ++j) { // 按列// 使用函数 emplace_back() 在数组 columns 的尾部添加新元素 -- pair(行索引 , 非零数值)columns[i * state_dim_ + j].emplace_back(i * state_dim_ + j, matrix_q_(j, j));++value_index;}}// 数组 columns 中 -- 稀疏矩阵 P 的右下角对角阵 diag(R , R , ... , R) 对应的部分(N个R)const size_t state_total_dim = state_dim_ * (horizon_ + 1);for (size_t i = 0; i < horizon_; ++i) { // 按 R 块for (size_t j = 0; j < control_dim_; ++j) { // 按列columns[i * control_dim_ + j + state_total_dim].emplace_back(i * control_dim_ + j + state_total_dim, matrix_r_(j, j));++value_index;}}// 到此为止得到完整的数组 columns ;// 临时变量// 作用:用来计数遍历到当前列(不包含该列)时,累计的非零元素的数量int ind_p = 0;// 使用数组 columns 得到数组 P_data / P_indices / P_indptr// 对于 P 矩阵,相当于按列遍历for (size_t i = 0; i < num_param_; ++i) { // 按列P_indptr->emplace_back(ind_p);for (const auto &row_data_pair : columns[i]) { // columns[i] 里的内容为第 i 列中所有非零元素的 pair 对P_data->emplace_back(row_data_pair.second);P_indices->emplace_back(row_data_pair.first);++ind_p;}}P_indptr->emplace_back(ind_p);
}// 函数作用:计算 q 矩阵
// 注意:车辆在每个时间步的目标状态量 x_ref 都是 0 向量,因为状态量本社就是误差量,我们的目的就是让误差量全为 0
void MpcOsqp::CalculateGradient() {gradient_ = Eigen::VectorXd::Zero(state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);for (size_t i = 0; i < horizon_ + 1; i++) {gradient_.block(i * state_dim_, 0, state_dim_, 1) = -1.0 * matrix_q_ * matrix_x_ref_;}
}// 函数作用:计算 A_c 矩阵,并将稀疏矩阵 A_c 表示为 csc_matrix(压缩列存储)格式
void MpcOsqp::CalculateEqualityConstraint(std::vector<c_float> *A_data, std::vector<c_int> *A_indices, std::vector<c_int> *A_indptr) {static constexpr double kEpsilon = 1e-6;Eigen::MatrixXd control_identity_mat = Eigen::MatrixXd::Identity(control_dim_, control_dim_);// 初始化矩阵 A_cEigen::MatrixXd matrix_constraint = Eigen::MatrixXd::Zero(state_dim_ * (horizon_ + 1) + state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, state_dim_ * (horizon_ + 1) + control_dim_ * horizon_);// 填充矩阵 A_cEigen::MatrixXd state_identity_mat = Eigen::MatrixXd::Identity(state_dim_ * (horizon_ + 1), state_dim_ * (horizon_ + 1));matrix_constraint.block(0, 0, state_dim_ * (horizon_ + 1), state_dim_ * (horizon_ + 1)) = -1 * state_identity_mat;for (size_t i = 0; i < horizon_; i++) {matrix_constraint.block((i + 1) * state_dim_, i * state_dim_, state_dim_, state_dim_) = matrix_a_;}for (size_t i = 0; i < horizon_; i++) {matrix_constraint.block((i + 1) * state_dim_, i * control_dim_ + (horizon_ + 1) * state_dim_, state_dim_, control_dim_) = matrix_b_;}Eigen::MatrixXd all_identity_mat = Eigen::MatrixXd::Identity(num_param_, num_param_);matrix_constraint.block(state_dim_ * (horizon_ + 1), 0, num_param_, num_param_) = all_identity_mat;// 将矩阵 A_c 表示为按列压缩格式std::vector<std::vector<std::pair<c_int, c_float>>> columns;columns.resize(num_param_ + 1);int value_index = 0;// 得到 columns 数组,用来后续辅助生成 3 个特征数组for (size_t i = 0; i < num_param_; ++i) { // colfor (size_t j = 0; j < num_param_ + state_dim_ * (horizon_ + 1); ++j) { // rowif (std::fabs(matrix_constraint(j, i)) > kEpsilon) {// (row, val)columns[i].emplace_back(j, matrix_constraint(j, i));++value_index;}}}// 求出按列压缩 A_c 的 3 个特征数组int ind_A = 0;for (size_t i = 0; i < num_param_; ++i) {A_indptr->emplace_back(ind_A);for (const auto &row_data_pair : columns[i]) {A_data->emplace_back(row_data_pair.second);A_indices->emplace_back(row_data_pair.first);++ind_A;}}A_indptr->emplace_back(ind_A);
}// 函数作用:计算约束向量 l 和 u
void MpcOsqp::CalculateConstraintVectors() {// 不等式约束形成的上下界:[xmin , xmin , ... , xmin | umin , umin , ... umin ]Eigen::VectorXd lowerInequality = Eigen::MatrixXd::Zero(state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);Eigen::VectorXd upperInequality = Eigen::MatrixXd::Zero(state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);// 控制量 u 的上下界for (size_t i = 0; i < horizon_; i++) {lowerInequality.block(control_dim_ * i + state_dim_ * (horizon_ + 1), 0, control_dim_, 1) = matrix_u_lower_;upperInequality.block(control_dim_ * i + state_dim_ * (horizon_ + 1), 0, control_dim_, 1) = matrix_u_upper_;}// 状态量 x 的上下界for (size_t i = 0; i < horizon_ + 1; i++) {lowerInequality.block(state_dim_ * i, 0, state_dim_, 1) = matrix_x_lower_;upperInequality.block(state_dim_ * i, 0, state_dim_, 1) = matrix_x_upper_;}// 等式约束形成的上下界:[ -x0 , 0 , 0 , ... , 0 ]Eigen::VectorXd lowerEquality = Eigen::MatrixXd::Zero(state_dim_ * (horizon_ + 1), 1);Eigen::VectorXd upperEquality;lowerEquality.block(0, 0, state_dim_, 1) = -1 * matrix_initial_x_;upperEquality = lowerEquality;lowerEquality = lowerEquality;// 合并等式约束和不等式约束lowerBound_ = Eigen::MatrixXd::Zero(2 * state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);lowerBound_ << lowerEquality, lowerInequality;upperBound_ = Eigen::MatrixXd::Zero(2 * state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);upperBound_ << upperEquality, upperInequality;
}// 函数作用:配置 QP 问题的参数
// 注1:返回值是一个 OSQPSettings 结构体的指针
// 注2:OSQPSettings 是 OSQP 库中的一个结构体,用于配置 OSQP 求解器的参数,该结构体中的所有属性都是 QP 问题的参数
// 注3:osqp_set_default_settings 是 OSQP 中的一个函数,作用为将指针指向的 OSQPSettings 结构体初始化为默认的设置值,用户可以根据具体需求进行调整
OSQPSettings* MpcOsqp::Settings() {// 分配内存:// 解释:c_malloc 函数作用是分配内存并返回一个 void* 类型的指针,并使用 reinterpret_cast 函数将指针类型强制转化为 OSQPSettings* 类型OSQPSettings* settings = reinterpret_cast<OSQPSettings *>(c_malloc(sizeof(OSQPSettings)));// 指针为空代表分配内存失败if (settings == nullptr) {return nullptr;}else {osqp_set_default_settings(settings);settings->polish = true;settings->scaled_termination = true;settings->verbose = false;settings->max_iter = max_iteration_; // QP 最大迭代次数settings->eps_abs = eps_abs_; // QP 计算精度return settings;}
}// 函数作用:配置 QP 问题的矩阵和向量
// 注1:返回值是一个 OSQPData 结构体的指针
// 注2:OSQPData 是 OSQP 库中的一个结构体,用于存储二次规划(QP)问题的输入数据,OSQPData 包含了定义 QP 问题所需的所有矩阵和向量
OSQPData* MpcOsqp::Data() {// 分配内存:OSQPData* data = reinterpret_cast<OSQPData *>(c_malloc(sizeof(OSQPData)));size_t kernel_dim = state_dim_ * (horizon_ + 1) + control_dim_ * horizon_; // QP 问题需要求解的变量的数量【( x_0 ~ x_N ) + ( u_0 ~ u_N-1 )】size_t num_affine_constraint = 2 * state_dim_ * (horizon_ + 1) + control_dim_ * horizon_; // QP 问题约束的数量if (data == nullptr) {return nullptr;}else {data->n = kernel_dim; // 需要求解的变量的数量data->m = num_affine_constraint; // 约束的数量 = 等式约束的数量 + 不等式约束的数量// 初始化稀疏矩阵 P 的 3 个特征数组std::vector<c_float> P_data;std::vector<c_int> P_indices;std::vector<c_int> P_indptr;// 计算稀疏矩阵 P 的 3 个特征数组CalculateKernel(&P_data, &P_indices, &P_indptr);// 通过 3 个特征数组计算出 P 阵,并将 P 阵传入data->P = csc_matrix(kernel_dim, kernel_dim, P_data.size(), CopyData(P_data), CopyData(P_indices), CopyData(P_indptr));// 将数组 q 传入data->q = gradient_.data();// 初始化稀疏矩阵 A_c 的 3 个特征数组std::vector<c_float> A_data;std::vector<c_int> A_indices;std::vector<c_int> A_indptr;// 计算稀疏矩阵 A_c 的 3 个特征数组CalculateEqualityConstraint(&A_data, &A_indices, &A_indptr);// 通过 3 个特征数组计算出 A_c 阵,并将 A_c 阵传入data->A = csc_matrix(state_dim_ * (horizon_ + 1) + state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, kernel_dim, A_data.size(), CopyData(A_data), CopyData(A_indices), CopyData(A_indptr));// 将上下界约束 l 和 u 传入data->l = lowerBound_.data();data->u = upperBound_.data();return data;}
}// 函数作用:释放 data 指针指向位置的内存
// 注:使用 c_malloc 函数分配内存,使用 c_free 函数释放内存,这两个函数是配套使用的
void MpcOsqp::FreeData(OSQPData* data) {c_free(data->A);c_free(data->P);c_free(data);
}// 函数作用:求解 QP 问题
// 返回值:当前时刻的控制命令
bool MpcOsqp::Solve(std::vector<double>* control_cmd) {CalculateGradient();CalculateConstraintVectors();OSQPData* data = Data();OSQPSettings* settings = Settings();// 注:OSQPWorkspace 是 OSQP 库中的一个类,用于管理和操作 OSQP 求解器的工作空间,包括定义问题、设置参数、执行求解等功能;这里创建了一个名为 osqp_workspace 的指针指向了这个工作空间OSQPWorkspace* osqp_workspace = nullptr;// 注:osqp_setup 函数是用来初始化 OSQP 求解器的工作空间的函数;这个函数的作用是根据传入的数据(data)和设置(settings)来设置和配置 OSQP 求解器的工作环境,以便后续能够使用 OSQP 求解器来解决具体的凸二次规划问题osqp_workspace = osqp_setup(data, settings);// 注:osqp_solve 函数的作用是调用 OSQP 求解器来解决已经设置好的凸二次规划问题;osqp_solve(osqp_workspace) 表示你正在使用 osqp_workspace 所指向的 OSQP 求解器工作空间来执行求解操作osqp_solve(osqp_workspace);// 完成求解后,求解过程中涉及的所有信息都会存储在 workspace 的 info 中,获得的结果都会存储在在 workspace 的 solution 中;// 这里取出了求解器的状态信息:// 1. 求解器状态小于 0:表示求解过程中出现了错误或者未能达到收敛状态// 2. 求解器状态为 1:表示求解器已经收敛并找到了最优解// 3. 求解器状态为 2:表示求解器达到了最大迭代次数而停止auto status = osqp_workspace->info->status_val;if (status < 0 || (status != 1 && status != 2)) {osqp_cleanup(osqp_workspace);FreeData(data);c_free(settings);return false;}else if (osqp_workspace->solution == nullptr) {// 注:如果 solution 为 nullptr,表示求解器没有成功生成解osqp_cleanup(osqp_workspace);FreeData(data);c_free(settings);return false;}size_t first_control = state_dim_ * (horizon_ + 1); // 第一个控制量所在位置的索引值// 因为 QP 问题的变量是 [ x_0 , x_1 , ... , x_N-1 ,x_N | u_0 , u_1 , ... , u_N-1 ]// 而我们需要的只是当前时刻的控制量 u_0 ,而 u_0 在变量中的位置的索引是 6*(N+1)// 给控制命令赋值为 u_0for (size_t i = 0; i < control_dim_; ++i) {control_cmd->at(i) = osqp_workspace->solution->x[i + first_control];}// 清理内存osqp_cleanup(osqp_workspace);FreeData(data);c_free(settings);return true;
}} // namespace control
} // namespace shenlan- 头文件 reference_line.h :补全参考线信息
#include <vector>
#include <iostream>
#include <math.h>
namespace shenlan {
namespace control {class ReferenceLine {
public:ReferenceLine(const std::vector<std::pair<double, double>>& xy_points);~ReferenceLine() = default;// 函数作用:计算参考线。参考线的每个点需要包含以下信息// 1) xy_pionts_ 路径点坐标// 2) headings 路径点朝向角// 3) accumulated_s 路径点累计路程// 4) kappas 路径点曲率// 5) dkappas 路径点曲率的变化率bool ComputePathProfile(std::vector<double>* headings, std::vector<double>* accumulated_s, std::vector<double>* kappas, std::vector<double>* dkappas);private:std::vector<std::pair<double, double>> xy_points_; // 用vector装载规划的全局路径上所有点的坐标
};} // namespace control
} // namespace shenlan- 源文件 reference_line.cpp :
#include "reference_line.h"
namespace shenlan {
namespace control {// 函数作用:拷贝构造函数
ReferenceLine::ReferenceLine(const std::vector<std::pair<double, double>>& xy_points) { xy_points_ = xy_points; }// 函数作用:由于全局路径规划期仅仅给出了全局路径信息(即所有点的xy坐标),而没有任何关于这条全局路径的其他几何信息(如每个路径点的 朝向角/距离/曲率/曲率变化率);
// 而我们在局部规划中使用的参考线其实是和全局路径重合的,也就是说参考线上的所有路径点就是全局路径的所有路径点;
// 但是要注意,我们需要的参考线不能仅仅只有每个路径点的坐标,还需要有每个路径点的各个几何信息(如 朝向角/距离/曲率/曲率变化率);
// 因此我们直接计算全局路径中每个路径点的几何信息,然后汇总到一起,就是我们需要的参考线信息;
bool ReferenceLine::ComputePathProfile(std::vector<double>* headings, std::vector<double>* accumulated_s, std::vector<double>* kappas, std::vector<double>* dkappas) {headings->clear(); // 装载每个路径点的 -- 朝向角accumulated_s->clear(); // 装载每个路径点的 -- 到达该点时所累积的路径长度(起点到该点的几何路径长度)kappas->clear(); // 装载每个路径点的 -- 曲率dkappas->clear(); // 装载每个路径点的 -- 曲率变化率if (xy_points_.size() < 2) return false;std::vector<double> dxs; // 路径点处的 -- dxstd::vector<double> dys; // 路径点处的 -- dystd::vector<double> y_over_s_first_derivatives; // 路径点处的 -- 一阶偏x导数std::vector<double> x_over_s_first_derivatives; // 路径点处的 -- 一阶偏y导数std::vector<double> y_over_s_second_derivatives; // 路径点处的 -- 二阶偏x导数std::vector<double> x_over_s_second_derivatives; // 路径点处的 -- 二阶偏y导数// 计算每个路径点的x,y差值(即dx,dy)std::size_t points_size = xy_points_.size();for (std::size_t i = 0; i < points_size; ++i) {double x_delta = 0.0;double y_delta = 0.0;if (i == 0) {x_delta = (xy_points_[i + 1].first - xy_points_[i].first);y_delta = (xy_points_[i + 1].second - xy_points_[i].second);} else if (i == points_size - 1) {x_delta = (xy_points_[i].first - xy_points_[i - 1].first);y_delta = (xy_points_[i].second - xy_points_[i - 1].second);} else {x_delta = 0.5 * (xy_points_[i + 1].first - xy_points_[i - 1].first);y_delta = 0.5 * (xy_points_[i + 1].second - xy_points_[i - 1].second);}dxs.push_back(x_delta);dys.push_back(y_delta);}// 计算每个路径点的朝向角for (std::size_t i = 0; i < points_size; ++i) {headings->push_back(std::atan2(dys[i], dxs[i]));}// 计算每个路径点处的累计路径长度double distance = 0.0;accumulated_s->push_back(distance); // 第一个路径点(起点)的 index = 0 ,且在该点处的累计路径长度为 0double fx = xy_points_[0].first; // 起点横坐标double fy = xy_points_[0].second; // 起点纵坐标double nx = 0.0;double ny = 0.0;for (std::size_t i = 1; i < points_size; ++i) {nx = xy_points_[i].first;ny = xy_points_[i].second;double end_segment_s = std::sqrt((fx - nx) * (fx - nx) + (fy - ny) * (fy - ny));accumulated_s->push_back(end_segment_s + distance);distance += end_segment_s;fx = nx;fy = ny;}// 计算每个路径点相对于路径长度ds的x和y的一阶导数for (std::size_t i = 0; i < points_size; ++i) {double xds = 0.0;double yds = 0.0;if (i == 0) {xds = (xy_points_[i + 1].first - xy_points_[i].first) / (accumulated_s->at(i + 1) - accumulated_s->at(i));yds = (xy_points_[i + 1].second - xy_points_[i].second) / (accumulated_s->at(i + 1) - accumulated_s->at(i));} else if (i == points_size - 1) {xds = (xy_points_[i].first - xy_points_[i - 1].first) / (accumulated_s->at(i) - accumulated_s->at(i - 1));yds = (xy_points_[i].second - xy_points_[i - 1].second) / (accumulated_s->at(i) - accumulated_s->at(i - 1));} else {xds = (xy_points_[i + 1].first - xy_points_[i - 1].first) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));yds = (xy_points_[i + 1].second - xy_points_[i - 1].second) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));}x_over_s_first_derivatives.push_back(xds);y_over_s_first_derivatives.push_back(yds);}// 计算每个路径点相对于路径长度ds的x和y的二阶导数for (std::size_t i = 0; i < points_size; ++i) {double xdds = 0.0;double ydds = 0.0;if (i == 0) {xdds = (x_over_s_first_derivatives[i + 1] - x_over_s_first_derivatives[i]) / (accumulated_s->at(i + 1) - accumulated_s->at(i));ydds = (y_over_s_first_derivatives[i + 1] - y_over_s_first_derivatives[i]) / (accumulated_s->at(i + 1) - accumulated_s->at(i));} else if (i == points_size - 1) {xdds = (x_over_s_first_derivatives[i] - x_over_s_first_derivatives[i - 1]) / (accumulated_s->at(i) - accumulated_s->at(i - 1));ydds = (y_over_s_first_derivatives[i] - y_over_s_first_derivatives[i - 1]) / (accumulated_s->at(i) - accumulated_s->at(i - 1));} else {xdds = (x_over_s_first_derivatives[i + 1] - x_over_s_first_derivatives[i - 1]) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));ydds = (y_over_s_first_derivatives[i + 1] - y_over_s_first_derivatives[i - 1]) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));}x_over_s_second_derivatives.push_back(xdds);y_over_s_second_derivatives.push_back(ydds);}// 计算每个路径点处的曲率for (std::size_t i = 0; i < points_size; ++i) {double xds = x_over_s_first_derivatives[i];double yds = y_over_s_first_derivatives[i];double xdds = x_over_s_second_derivatives[i];double ydds = y_over_s_second_derivatives[i];double kappa = (xds * ydds - yds * xdds) / (std::sqrt(xds * xds + yds * yds) * (xds * xds + yds * yds) + 1e-6);// 注1:曲率计算公式的分母上加上一个很小的数,防止除法失效// 注2:这里对曲率的计算使用的是精确公式,而代码中我们在进行动力学建模,计算连续误差型状态空间方程的状态量x时(如:航向误差变化率),则是将曲率视为了半径的倒数,这是一种对曲率的估算方式;kappas->push_back(kappa);}// 计算每个路径点处的曲率变化率for (std::size_t i = 0; i < points_size; ++i) {double dkappa = 0.0;if (i == 0) {dkappa = (kappas->at(i + 1) - kappas->at(i)) / (accumulated_s->at(i + 1) - accumulated_s->at(i));} else if (i == points_size - 1) {dkappa = (kappas->at(i) - kappas->at(i - 1)) / (accumulated_s->at(i) - accumulated_s->at(i - 1));} else {dkappa = (kappas->at(i + 1) - kappas->at(i - 1)) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));}dkappas->push_back(dkappa);}return true;
}} // namespace control
} // namespace shenlan- 主函数:
#include "mpc_controller.h"
using namespace std;bool first_record_ = true; // 起点标志
VehicleState vehicle_state_; // 车辆状态
ControlCmd cmd_pub; // 控制命令
ros::Publisher acc_pub; // 声明了一个 ROS 发布者对象【将信息发布到一个或多个主题(Topic)上,使得其他 ROS 节点可以订阅(Subscribe)并接收这些消息】// 函数作用:通过读取 IMU 传感器的数据,得到车辆当前的姿态信息
void IMUCallback(const sensor_msgs::Imu::ConstPtr& msg) {// 角速度(绕z轴转动的角速度)vehicle_state_.angular_velocity = msg->angular_velocity.z;// 加速度(线性加速度)vehicle_state_.acceleration = sqrt(msg->linear_acceleration.x * msg->linear_acceleration.x + msg->linear_acceleration.y * msg->linear_acceleration.y);
}// 函数作用:通过读取 ODOM 传感器的数据,得到车辆当前的位置信息
void odomCallback(const nav_msgs::Odometry::ConstPtr& msg) {if(first_record_) {vehicle_state_.planning_init_x = msg->pose.pose.position.x;vehicle_state_.planning_init_y = msg->pose.pose.position.y;first_record_ = false;}vehicle_state_.x = msg->pose.pose.position.x;vehicle_state_.y = msg->pose.pose.position.y;vehicle_state_.last_velocity = vehicle_state_.velocity;vehicle_state_.last_v_time = vehicle_state_.cur_v_time;vehicle_state_.last_v_err = vehicle_state_.last_velocity - 5;// 将 ROS 消息中的姿态信息(四元数表示的 orientation)转换为欧拉角(roll, pitch, yaw)形式,并存储到 vehicle_state_ 结构体的对应成员变量中// 1. 声明了一个名为 q 的 tf::Quaternion 类型的变量,用于存储姿态信息的四元数表示;tf::Quaternion q;// 2. 将 ROS 消息中的姿态信息(msg->pose.pose.orientation)转换为 tf::Quaternion 类型并放在 q 变量内;// quaternionMsgToTF() 是一个 ROS 中的函数,用于将 ROS 消息中的四元数表示转换为 TF 库中的四元数表示;tf::quaternionMsgToTF(msg->pose.pose.orientation, q);// 3. 将 q 转换为一个 3x3 的旋转矩阵,然后调用 getRPY 方法,将该旋转矩阵转换为欧拉角(Roll, Pitch, Yaw),并存储到 vehicle_state_ 的对应成员变量中;tf::Matrix3x3(q).getRPY(vehicle_state_.roll, vehicle_state_.pitch, vehicle_state_.yaw);vehicle_state_.heading = vehicle_state_.yaw;vehicle_state_.velocity = std::sqrt(msg->twist.twist.linear.x * msg->twist.twist.linear.x + msg->twist.twist.linear.y * msg->twist.twist.linear.y);vehicle_state_.cur_v_err = vehicle_state_.velocity - 5;vehicle_state_.cur_v_time = ros::Time::now().toSec(); // 利用 ROS 提供的时间函数获取当前系统时间,并将其转换为秒数
}// 主函数
int main(int argc, char** argv) {// 声明文件流对象,用于打开和读取文件:std::ifstream infile;infile.open("src/mpc_control/data/reference_line.txt"); // 将文件流对象与文件连接起来assert(infile.is_open()); // 若失败,则输出错误消息,并终止程序运行std::vector<std::pair<double, double>> xy_points; // 存放所有参考点的坐标std::string x; // 临时变量std::string y; // 临时变量std::string s; // 使用该变量逐行读取文件内容while (getline(infile, s)) {std::stringstream word(s);word >> x;word >> y;double pt_x = std::atof(x.c_str());double pt_y = std::atof(y.c_str());xy_points.push_back(std::make_pair(pt_x, pt_y));}// 关闭文件流:infile.close();// 补全每个参考点的信息:(当前只有每个参考点的位置坐标)std::vector<double> headings;std::vector<double> accumulated_s;std::vector<double> kappas;std::vector<double> dkappas;std::unique_ptr<shenlan::control::ReferenceLine> reference_line = std::make_unique<shenlan::control::ReferenceLine>(xy_points);reference_line->ComputePathProfile(&headings, &accumulated_s, &kappas, &dkappas);// 通过参考线信息构建目标轨迹:TrajectoryData planning_published_trajectory;for (size_t i = 0; i < headings.size(); i++) {TrajectoryPoint trajectory_pt;trajectory_pt.x = xy_points[i].first;trajectory_pt.y = xy_points[i].second;trajectory_pt.v = 5.0; // 目标速度trajectory_pt.a = 0.0; // 目标加速度trajectory_pt.heading = headings[i];trajectory_pt.kappa = kappas[i];planning_published_trajectory.trajectory_points.push_back(trajectory_pt);}// 使用 ROS 的 API 进行初始化和设置 ROS 节点的基本步骤// 1. ros::init 是 ROS 提供的初始化函数,用于初始化 ROS 系统;它需要传入命令行参数 argc 和 argv 以及一个节点名称 control_pub ;ros::init(argc, argv, "control_pub");// 2. ros::NodeHandle 是 ROS 中的一个类,用于与 ROS 系统进行通信;这里创建了一个名为 nh 的 NodeHandle 对象,用于管理 ROS 节点的通信和资源;ros::NodeHandle nh;// 3. ROS_INFO 是 ROS 提供的一个宏,用于打印消息到ROS的日志系统中,这里表示节点初始化完成;ROS_INFO("init !");// 4. subscribe 是 NodeHandle 对象的方法,用于订阅ROS主题;// 这行代码创建了一个名为 sub 的订阅者对象,订阅了主题 "/odom" ,缓冲区大小为 10 ,回调函数为 odomCallback;当节点收到来自 "/odom" 主题的消息时,将调用 odomCallback 函数进行处理;ros::Subscriber sub = nh.subscribe("/odom", 10, odomCallback);// 5. 创建了一个名为 sub_imu 的订阅者对象,订阅了主题 "/imu_raw" ,缓冲区大小为 10 ,回调函数为 IMUCallback;当节点收到来自 "/imu_raw" 主题的消息时,将调用 IMUCallback 函数进行处理;ros::Subscriber sub_imu = nh.subscribe("/imu_raw", 10, IMUCallback);// 6. advertise 是 NodeHandle 对象的方法,用于发布ROS主题;// 这行代码创建了一个名为 control_pub 的发布者对象,发布类型为 lgsvl_msgs::VehicleControlData 的消息到主题 "/vehicle_cmd",并指定了发布队列的大小为1000 ;// 这意味着节点可以同时缓存 1000 条待发布的消息,超过这个数量后新的消息将被丢弃;ros::Publisher control_pub = nh.advertise<lgsvl_msgs::VehicleControlData>("/vehicle_cmd", 1000);// 7. 在 ROS 中创建了一个新的发布者对象 acc_pub ,用于向主题 "/acc_pub_cmd" 发布消息类型为 lgsvl_msgs::VehicleControlData 的数据;acc_pub = nh.advertise<lgsvl_msgs::VehicleControlData>("/acc_pub_cmd", 1000);// MPC 控制部分:ControlCmd cmd;std::unique_ptr<shenlan::control::MPCController> mpc_controller = std::make_unique<shenlan::control::MPCController>();mpc_controller->Init();lgsvl_msgs::VehicleControlData control_cmd;lgsvl_msgs::VehicleControlData control_cmd_pub; ros::Rate loop_rate(100);while (ros::ok()) {mpc_controller->ComputeControlCommand(vehicle_state_, planning_published_trajectory, cmd);control_cmd.header.stamp = ros::Time::now();cout << "vehical_state_.last_v_err: " << vehicle_state_.last_v_err << endl;cout << "vehical_state_.cur_v_err: " << vehicle_state_.cur_v_err << endl;cout << "cur_acc: " << (vehicle_state_.cur_v_err - vehicle_state_.last_v_err) / (vehicle_state_.cur_v_time - vehicle_state_.last_v_time) << endl;cout << "cmd.acc: " << cmd.acc << endl;control_cmd.acceleration_pct = cmd.acc;control_cmd.target_gear = lgsvl_msgs::VehicleControlData::GEAR_DRIVE;control_cmd.target_wheel_angle = -cmd.steer_target;control_pub.publish(control_cmd);control_cmd_pub.acceleration_pct = vehicle_state_.acceleration;acc_pub.publish(control_cmd_pub);ros::spinOnce();loop_rate.sleep();}return 0;
}
相关文章:
第5章:模型预测控制(MPC)的代码实现
1. 建立 QP 模型: 1.1 车辆模型: 注:使用车辆横向动力学模型 纵向动力学模型(误差模型) 1.2 QP 问题模型: 注:详细推导见 笔记100:使用 OSQP-Eigen 对 MPC 进行求解的方法与代码-…...
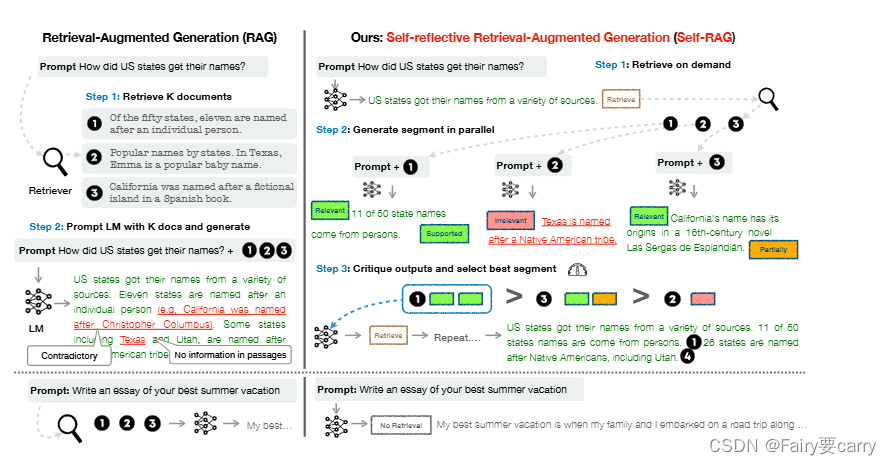
论文学习day01
1.自我反思的检索增强生成(SELF-RAG) 1.文章出处: Chan, C., Xu, C., Yuan, R., Luo, H., Xue, W., Guo, Y., & Fu, J. (2024). RQ-RAG: Learning to Refine Queries for Retrieval Augmented Generation. ArXiv, abs/2404.00610. 2.摘…...

Github入门教程,适合新手学习(非常详细)
前言:本篇博客为手把手教学的 Github 代码管理教程,属于新手入门级别的难度。教程简单易操作,能够基本满足读者朋友日常项目寄托于 Github 平台上进行代码管理的需求。Git 与 Github 是一名合格程序员 coder 必定会接触到的工具与平台&#x…...

C# OpenCvSharp 代数运算-add、scaleAdd、addWeighted、subtract、absdiff、multiply、divide
在C#中使用OpenCvSharp进行图像处理时,理解和合理使用各种图像操作函数可以帮助我们实现许多实际应用中的需求。下面,我将详细介绍每个函数的使用,并给出与实际应用项目相关的示例,包括运算过程和运算结果。 1. add 函数 作用 将两幅图像进行相加,可以达到图像融合的目的…...

为什么说Python 是胶水语言?
"Python 是胶水语言"这一说法是指它很擅长将不同的程序或代码库连接在一起,能够让来自不同编程语言或框架的组件无缝协作。Python 具有丰富的库和简单的语法,使得它可以轻松调用其他语言编写的程序或使用不同技术栈的模块。 以下是几个…...

GitLab教程(二):快速上手Git
文章目录 1.将远端代码克隆到本地2.修改本地代码并提交到远程仓库3.Git命令总结git clonegit statusgit addgit commitgit pushgit log 首先,我在Gitlab上创建了一个远程仓库,用于演示使用Gitlab进行版本管理的完整流程: 1.将远端代码克隆到本…...

结构体知识点
基本概念 结构体是一种自定义变量类型,类似于枚举需要自己定义。 它是数据和函数的集合。 在结构体中,可以声明各种变量和方法。 基本语法 1.结构体一般写在namespace语句块中。 2.结构体关键字struct struct 自定义结构体名 {//第一部分//变量//…...

C# —— 显示转换
显示转换: 通过一些方法可以将其他数据类型转换为我们想要的数据类型 1.括号强转 作用: 一般情况下 将高精度的类型转换为低精度 // 语法: 变量类型 变量名 (转换的变量类型名称) 变量; // 注意: 精度问题 范围问题 sbyte sb 1; short s 1; int …...
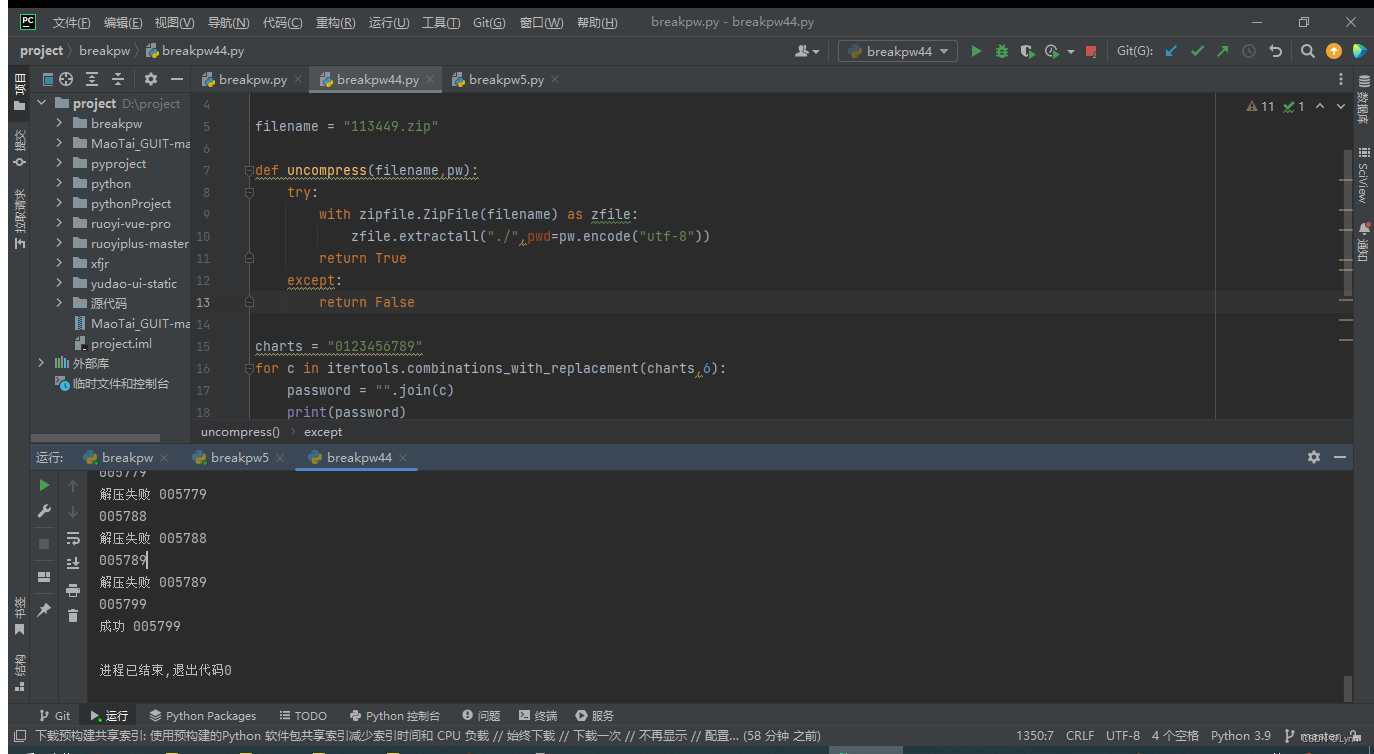
zip加密txt文件后,暴力破解时会有多个解密密码可以打开的疑问??
最近在做一个关于zip压缩文件解密的测试,发现通过暴力解密时,会有多个解密密码可以打开,非常疑惑,这里做个问题,希望能有大佬解惑。 1、首先在本地创建一个113449.txt的文件,然后右键txt文件选择压缩&…...

css入门宝典
3.1.4 通配符选择器 语法 : *{} 作用 : 让页面中所有的标签执行该样式,通常用来清除间距 例子 : *{ margin: 0; //外间距 padding: 0; //内间距 } 一 CSS基本语法 1基础知识 1.1概述 Css (层叠样式表)是种格式化网页的标准方式, 用于控制设置网页的样式ÿ…...

【AI原理解析】— 星火大模型
目录 1. 模型基础架构 神经网络结构 编码器 解码器 多层神经网络结构 其他自然语言处理技术 2. 训练数据 来源 规模 3. 自监督学习 Masked Language Model (MLM) 4. 参数量与计算能力 大规模参数量 深度学习算法 5. 技术特点 多模态输入 自我学习与迭代 6. 应…...

StarNet实战:使用StarNet实现图像分类任务(一)
文章目录 摘要安装包安装timm 数据增强Cutout和MixupEMA项目结构计算mean和std生成数据集 摘要 https://arxiv.org/pdf/2403.19967 论文主要集中在介绍和分析一种新兴的学习范式——星操作(Star Operation),这是一种通过元素级乘法融合不同子…...

单链表——AcWing.826单链表
单链表 定义 单链表是一种常见的数据结构,它由一系列节点组成,每个节点包含一个数据元素和一个指向下一个节点的指针。 运用情况 用于实现动态的数据存储和管理,例如实现栈、队列等其他数据结构。在需要频繁进行插入和删除操作时非常有用…...

10:Hello, World!的大小
OpenJudge - 10:Hello, World!的大小 描述 还记得在上一章里,我们曾经输出过的“Hello, World!”吗? 它虽然不是本章所涉及的基本数据类型的数据,但我们同样可以用sizeof函数获得它所占用的空间大小。 请编程求出它的大小,看看跟你…...

【Pandas驯化-03】Pandas中常用统计函数mean、count、std、info使用
【Pandas驯化-03】Pandas中常用统计函数mean、count、std、info使用 本次修炼方法请往下查看 🌈 欢迎莅临我的个人主页 👈这里是我工作、学习、实践 IT领域、真诚分享 踩坑集合,智慧小天地! 🎇 相关内容文档获取 微…...
WordPress——Argon主题美化
文章目录 Argon主题美化插件类类别标签页面更新管理器文章头图URL查询监视器WordPress提供Markdown语法评论区头像设置发信设置隐藏登陆备份设置缓存插件 主题文件编辑器页脚显示在线人数备案信息(包含备案信息网站运行时间)banner下方小箭头滚动效果站点功能概览下方Links功能…...
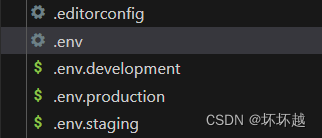
Vue部分文件说明
1.eslintignore文件 Eslint会忽略的文件 # Eslint 会忽略的文件.DS_Store node_modules dist dist-ssr *.local .npmrc 2.gitignore # Git 会忽略的文件.DS_Store node_modules dist dist-ssr .eslintcache# Local env files *.local# Logs logs *.log npm-debug.log* yarn-de…...
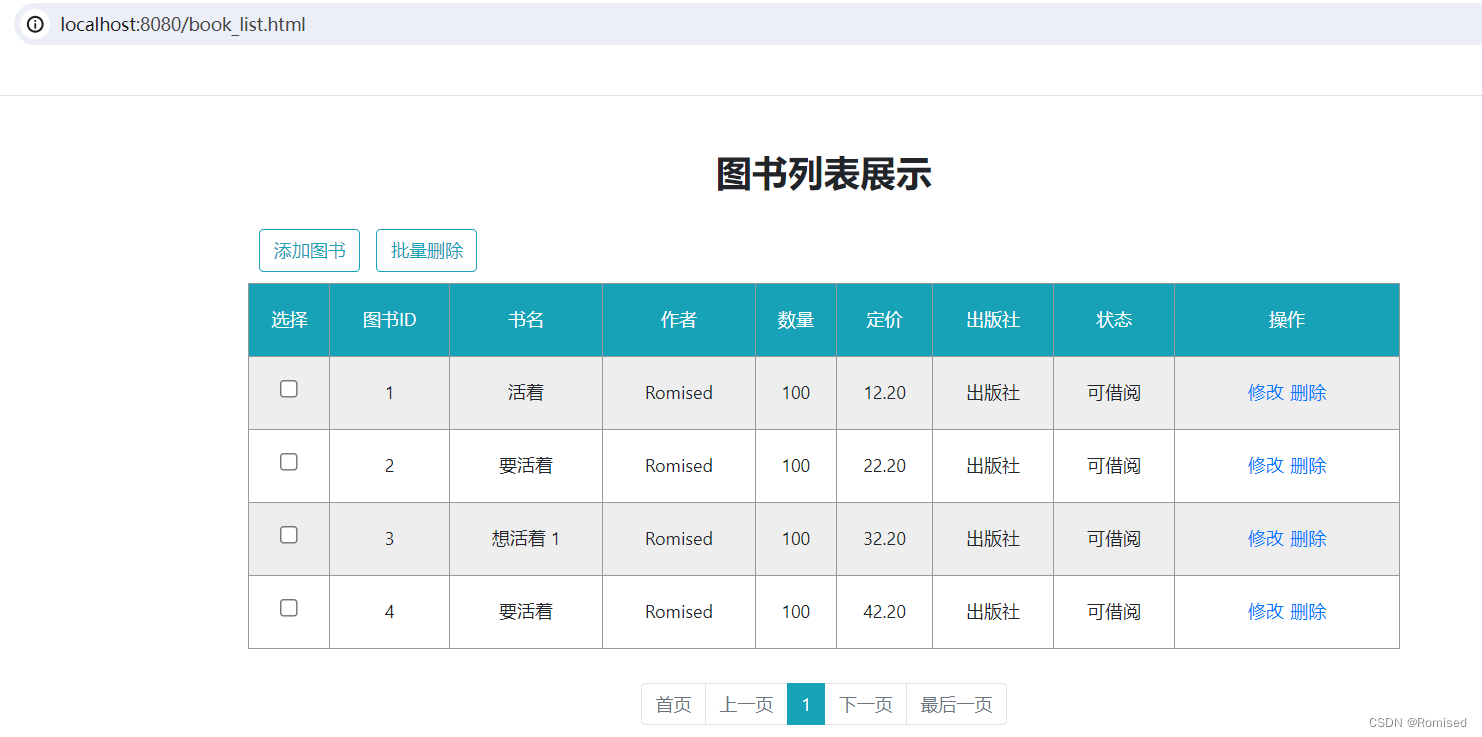
图书管理系统(SpringBoot+SpringMVC+MyBatis)
目录 1.数据库表设计 2.引入MyBatis和MySQL驱动依赖 3.配置数据库&日志 4.Model创建 5.用户登录功能实现 6.实现添加图书功能 7.实现翻页功能 1.数据库表设计 数据库表是应⽤程序开发中的⼀个重要环节, 数据库表的设计往往会决定我们的应⽤需求是否能顺利实现, 甚至决…...

11.泛型、trait和生命周期(上)
标题 一、泛型数据的引入二、改写为泛型函数三、结构体/枚举中的泛型定义四、方法定义中的泛型 一、泛型数据的引入 下面是两个函数,分别用来取得整型和符号型vector中的最大值 use std::fs::File;fn get_max_float_value_from_vector(src: &[f64]) -> f64…...
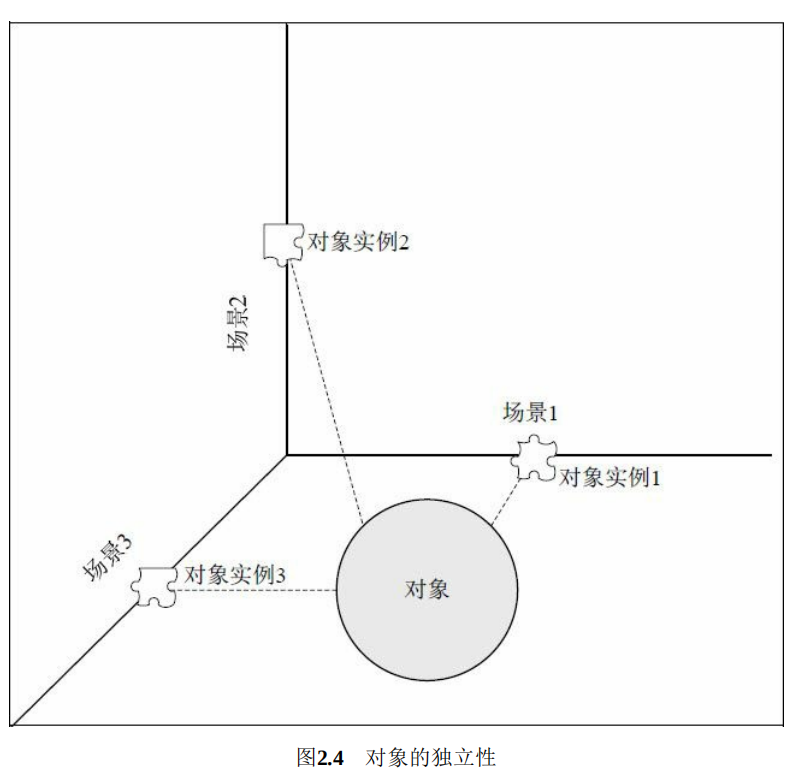
UML与设计模式
1、关联关系 关联关系用于描述不同类的对象之间的结构关系,它在一段时间内将多个类的实例连接在一起。关联关系是一种静态关系,通常与运行状态无关,而是由“常识”、“规则”、“法律”等因素决定的,因此关联关系是一种强关联的关…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
