Bio-Info每日一题:Rosalind-07-Mendel‘s First Law(孟德尔第一定律 python实现)
🎉 进入生物信息学的世界,与Rosalind一起探索吧!🧬
Rosalind是一个在线平台,专为学习和实践生物信息学而设计。该平台提供了一系列循序渐进的编程挑战,帮助用户从基础到高级掌握生物信息学知识。无论你是初学者还是专业人士,Rosalind都能为你提供适合的学习资源和实践机会。网址:https://rosalind.info
你是否想像专业人士一样分析DNA序列?这里有一个简单的任务来帮助你入门。
📝 任务说明:

这个题目是要你计算在一群具有不同基因型的个体中,两两随机交配后,后代中表现显性性状的概率。题目给出了三种基因型的个体数量:
- k: 纯合显性个体的数量(homozygous dominant, AA)
- m: 杂合个体的数量(heterozygous, Aa)
- n: 纯合隐性个体的数量(homozygous recessive, aa)
需要计算两两随机选取个体交配后,后代表现显性性状(具有显性等位基因)的概率。
解答
可能的配对及其概率:
-
AA×AA:总是产生 AA(100% 显性)
-
AA×Aa(或 Aa×AA):产生 50% AA 和 50% Aa(100% 显性)
-
AA×aa(或 aa×AA):总是产生 Aa(100% 显性)
-
Aa×Aa:产生 25% AA、50% Aa 和 25% aa(75% 显性)
-
Aa×aa(或 aa×Aa):产生 50% Aa 和 50% aa(50% 显性)
-
aa×aa:总是产生 aa(0% 显性)
每种配对的概率计算

-
计算最终的概率:
- 最终的概率是上述每种配对概率与其产生显性表型概率的乘积之和。
def dominant_phenotype_probability(k, m, n):# 总个体数total = k + m + n# 各种配对产生显性表型的概率prob_AA_AA = (k / total) * ((k - 1) / (total - 1))prob_AA_Aa = 2 * (k / total) * (m / (total - 1))prob_AA_aa = 2 * (k / total) * (n / (total - 1))prob_Aa_Aa = (m / total) * ((m - 1) / (total - 1))prob_Aa_aa = 2 * (m / total) * (n / (total - 1))prob_aa_aa = (n / total) * ((n - 1) / (total - 1))# 显性表型的总概率probability = (prob_AA_AA * 1 +prob_AA_Aa * 1 +prob_AA_aa * 1 +prob_Aa_Aa * 0.75 +prob_Aa_aa * 0.5 +prob_aa_aa * 0)return probabilitydef main():# 从输入读取数据k = int(input("请输入显性纯合体(AA)的个体数: "))m = int(input("请输入杂合体(Aa)的个体数: "))n = int(input("请输入隐性纯合体(aa)的个体数: "))# 计算并打印概率result = dominant_phenotype_probability(k, m, n)print(f"产生显性表型后代的概率: {result:.5f}")if __name__ == "__main__":main()补充
孟德尔第一定律,也称为分离律(Law of Segregation),是孟德尔在研究豌豆遗传实验时发现的基本遗传定律之一。该定律描述了在生殖细胞形成过程中,等位基因如何分离并在后代中重新组合的现象。具体内容如下:
-
等位基因分离:每个个体有一对等位基因控制某一特定性状(例如豌豆的颜色),这些等位基因在生殖细胞(配子)形成时会分离。每个配子只会携带其中一个等位基因。
-
随机组合:受精时,来自父本和母本的配子随机结合,从而形成新的基因型。这意味着后代的基因型是随机组合的,具有不同的等位基因组合。
孟德尔通过研究豌豆的性状,如花的颜色和种子的形状,发现了这种分离现象。具体来说,他注意到当他交配纯合显性个体和纯合隐性个体时,第一代子代(F1代)全部表现出显性性状,而第二代子代(F2代)则按3:1的比例分离出显性和隐性性状。
以下是对孟德尔第一定律的简要总结:
- 每个性状由一对等位基因控制。
- 在形成配子时,等位基因分离,每个配子只包含一个等位基因。
- 受精时,来自父母双方的等位基因随机结合,决定后代的基因型和表现型。
相关文章:

Bio-Info每日一题:Rosalind-07-Mendel‘s First Law(孟德尔第一定律 python实现)
🎉 进入生物信息学的世界,与Rosalind一起探索吧!🧬 Rosalind是一个在线平台,专为学习和实践生物信息学而设计。该平台提供了一系列循序渐进的编程挑战,帮助用户从基础到高级掌握生物信息学知识。无论你是初…...

C++ 47 之 函数调用运算符重载
#include <iostream> #include <string> using namespace std;class MyPrint{ public:// 重载小括号() 重载谁operator后就紧跟谁的符号void operator()(string txt){cout << txt << endl;} };class MyAdd{ public:int operator()(int a, int b){retur…...
[Qt的学习日常]--常用控件1
前言 作者:小蜗牛向前冲 名言:我可以接受失败,但我不能接受放弃 如果觉的博主的文章还不错的话,还请点赞,收藏,关注👀支持博主。如果发现有问题的地方欢迎❀大家在评论区指正 目录 一、什么是控…...
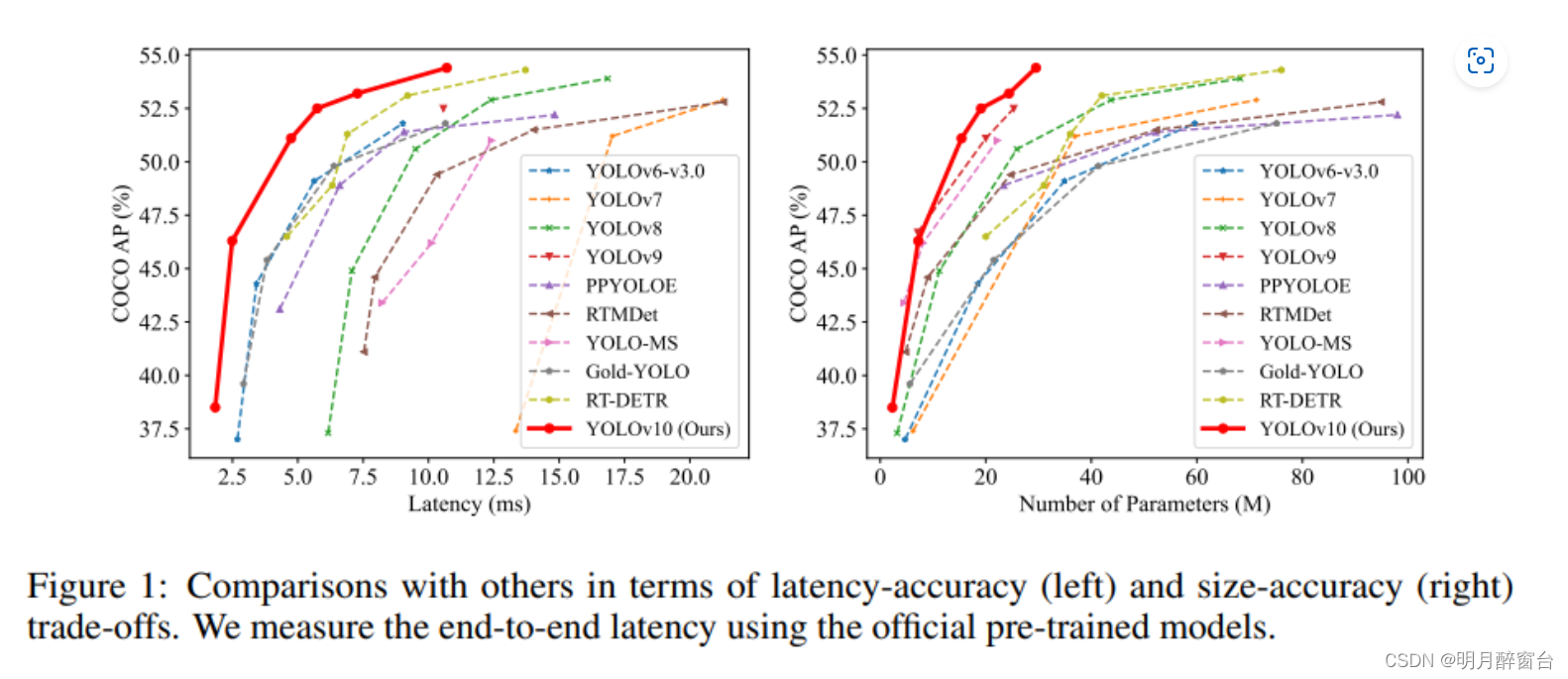
模型实战(23)之 yolov10 使用总结及训练自己的数据集
yolov10 使用总结及训练自己的数据集 0. yolov10 原理分析 此处参考:https://blog.csdn.net/CVHub/article/details/139204248论文:https://arxiv.org/pdf/2405.14458源码:https://github.com/THU-MIG/yolov10 论文原理分析: 创新: 双标签分配策略 众所周知,标签分配策略…...
AIRNet模型使用与代码分析(All-In-One Image Restoration Network)
AIRNet提出了一种较为简易的pipeline,以单一网络结构应对多种任务需求(不同类型,不同程度)。但在效果上看,ALL-In-One是不如One-By-One的,且本文方法的亮点是batch内选择patch进行对比学习。在与sota对比上…...

欧洲杯“球迷狂欢趴”开启,容声带来“健康养鲜”新理念
6月15日,容声冰箱在深圳举行了异彩纷呈的“欧洲杯养鲜补给站 球迷狂欢趴”系列活动。 容声国内营销总经理韩栋现场发布“以品质领先 为健康养鲜”的主题内容,强调容声将以健康养鲜技术产品的升级迭代,满足用户品质生活需求。 作为有着41年发…...

人工智能对零售业的影响
机器人、人工智能相关领域 news/events (专栏目录) 本文目录 一、人工智能如何改变零售格局二、利用人工智能实现购物体验自动化三、利用人工智能改善库存管理四、通过人工智能解决方案增强客户服务五、利用人工智能分析消费者行为六、利用 AI 打造个性化…...
Spring Boot + EasyExcel + SqlServer 进行批量处理数据
前言 在日常开发和工作中,我们可能要根据用户上传的文件做一系列的处理,本篇文章就以Excel表格文件为例,模拟用户上传Excel文件,讲述后端如何高效的进行数据的处理。 一.引入 EasyExcel 依赖 <!-- https://mvnrepository.com/…...
深入理解指针(四)
目录 1. 回调函数是什么? 2. qsort使用举例 2.1冒泡排序 2.2使用qsort函数排序整型数据 2.3 使用qsort排序结构数据(名字) 2.4 使用qsort排序结构数据(年龄) 3. qsort函数的模拟实现 1. 回调函数是什么? 回调函数就是⼀个通过函数指针调⽤的函数。 如果你把函数…...

k-means聚类模型的优缺点
一、k-means聚类模型的优点 1. 简单高效:k-means算法思想简单直观,易于实现。它通过迭代计算样本点与聚类中心之间的距离,并不断调整聚类中心的位置,直至满足终止条件。由于其计算过程相对直接,所以具有较高的执行效率…...
我的创作纪念日(1825天)
Ⅰ、机缘 1. 记得是大一、大二的时候就听学校的大牛说,可以通过写 CSDN 博客,来提升自己的代码和逻辑能力,虽然即将到了写作的第六个年头,但感觉这句话依旧受用; 2、今年一整年的创作都没有停止,本年度几乎是每周都来…...
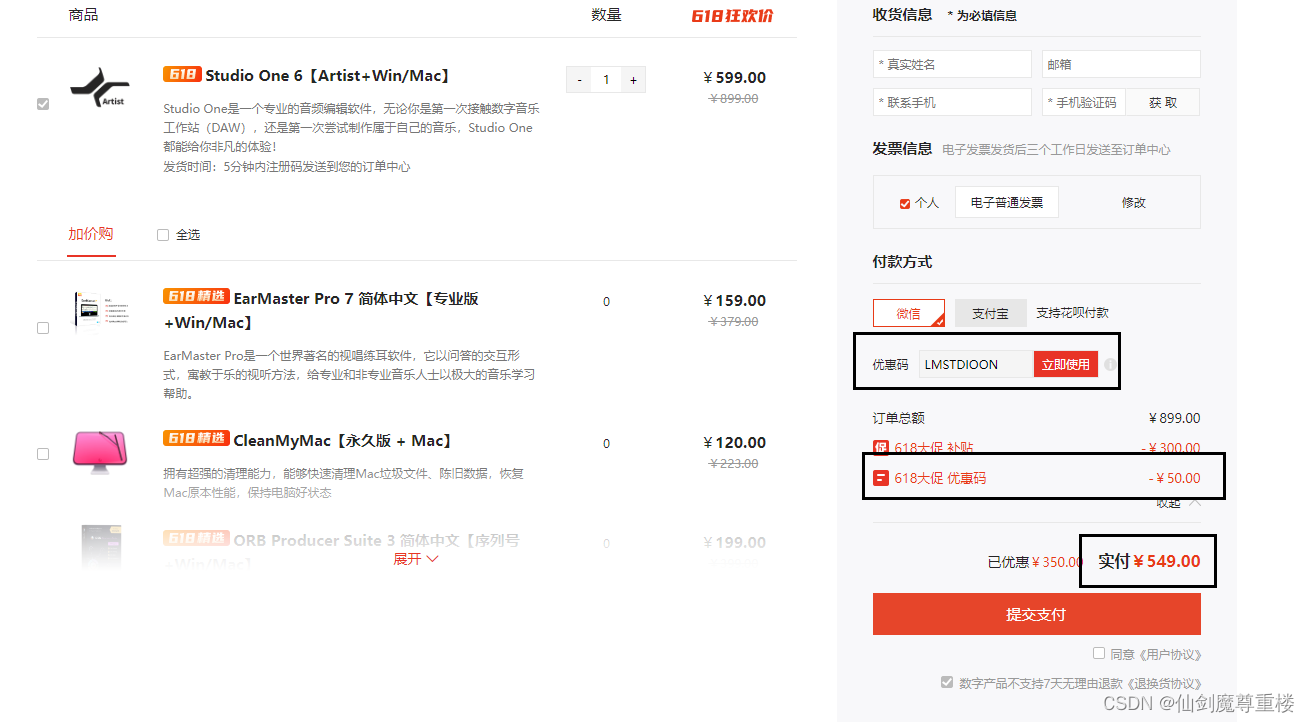
Studio One 6.6.2 for Mac怎么激活,有Studio One 6激活码吗?
如果您是一名音乐制作人,您是否曾经为了寻找一个合适的音频工作站而苦恼过?Studio One 6 for Mac是一款非常适合您的MacBook的音频工作站。它可以帮助您轻松地录制、编辑、混音和发布您的音乐作品。 Studio One 6.6.2 for Mac具有直观的界面和强大的功能…...
Windows搭建nacos集群
Nacos是阿里巴巴的产品,现在是SpringCloud中的一个组件。相比Eureka功能更加丰富,在国内受欢迎程度较高。 下载地址:Tags alibaba/nacos GitHub 链接:百度网盘 请输入提取码 提取码:8888 解压文件夹 目录说明&am…...

kotlin 中的字符
一、字符类型 1、kotlin中,字符用Char类型表示,值使用单引号 括起来。 fun main() {val a: Char 1println(a) // 1println("a类型为:${a.javaClass.simpleName}") // a类型为:char } 2、特殊字符的表示。 \t——制…...

yocto根文件系统如何配置静态IP地址
在Yocto根文件系统中配置静态IP地址,你可以参考以下步骤。请注意,这些步骤可能会因Yocto版本和具体硬件平台的不同而略有差异。 1. 获取网络配置信息 首先,你需要从网络运维方获取分配的IP地址、子网掩码、默认网关和DNS信息。 2. 确定配置文…...

【博客720】时序数据库基石:LSM Tree的辅助优化
时序数据库基石:LSM Tree的辅助优化 场景: LSM Tree其实本质是一种思想,而具体是否需要WAL,内存表用什么有序数据结构来组织,磁盘上的SSTable用什么结构来存放,是否需要布隆过滤器来加快不存在数据的判断等…...
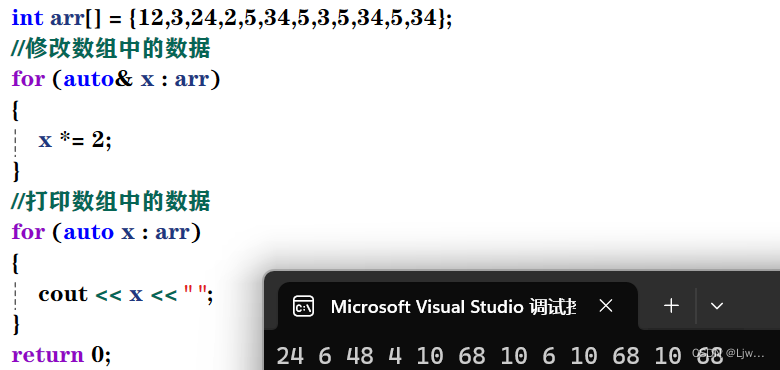
C++前期概念(重)
目录 命名空间 命名空间定义 1. 正常的命名空间定义 2. 命名空间可以嵌套 3.头文件中的合并 命名空间使用 命名空间的使用有三种方式: 1:加命名空间名称及作用域限定符(::) 2:用using将命名空间中某个成员引入 3:使用using namespa…...

Java字符串加密HMAC-SHA1密钥,转换成Base64编码
新建一个maven测试项目,直接把代码复制过去就行,把data和secretKey的值替换成想加密的值。 package test;import javax.crypto.Mac; import javax.crypto.spec.SecretKeySpec; import java.security.InvalidKeyException; import java.security.NoSuchA…...
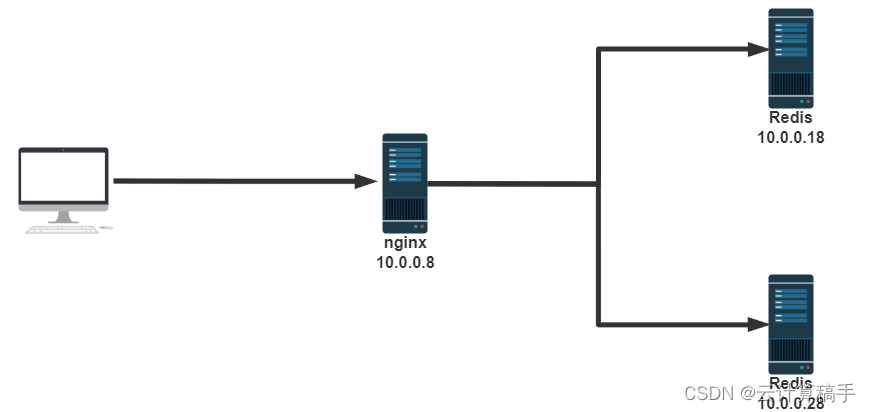
【网络架构】Nginx
目录 一、I/O模型 1.1 Linux 的 I/O 1.2 零拷贝技术 1.3 网络IO模型 1.3.1 阻塞型 I/O 模型(blocking IO)编辑 1.3.2非阻塞型 I/O 模型 (nonblocking IO)编辑 1.3.3 多路复用 I/O 型 ( I/O multiplexing )编辑 1.3.4 信号驱动式 I/O 模型 …...

C# OpenCvSharp 逻辑运算-bitwise_and、bitwise_or、bitwise_not、bitwise_xor
bitwise_and 函数 🤝 作用或原理: 将两幅图像进行与运算,通过逻辑与运算可以单独提取图像中的某些感兴趣区域。如果有掩码参数,则只计算掩码覆盖的图像区域。 示例: 在实际应用中,可以用 bitwise_and 来提取图像中的某些部分。例如,我们可以从图像中提取出一个特定的颜…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
