红黑树(C++)
文章目录
- 写在前面
- 1. 红黑树的概念及性质
- 1. 1 红黑树的概念
- 1. 2 红黑树的性质
- 2. 红黑树节点的定义
- 3. 红黑树的插入
- 3.1 按照二叉搜索的树规则插入新节点
- 3.2 检测新节点插入后,红黑树的性质是否造到破坏
- 4.红黑树的删除
- 5.红黑树的验证
- 6.源码
写在前面
在上篇文章中,我们实现了AVL树,AVL树是一种高度平衡的二叉搜索树。通过确保任何节点的左右子树的高度差不超过1,AVL树能够维持严格的平衡状态。然而,严格平衡的代价是某些插入和删除操作可能需要多次旋转。
本篇文章将实现红黑树,它是一种近似平衡的二叉搜索树。红黑树通过维持某些性质来保持树的平衡。通过这些性质,红黑树确保从根到叶子的所有路径中,最长路径不超过最短路径的两倍,从而实现近似平衡。这种近似平衡比AVL树的严格平衡稍松一些,使得它在某些插入和删除操作中的效率更高,因为它需要的旋转次数较少。
在接下来的内容中,我们将详细介绍红黑树的实现过程,以及它是如何通过旋转和重新着色来维护红黑树的平衡性。
1. 红黑树的概念及性质
1. 1 红黑树的概念
红黑树,是一种二叉搜索树,其每个节点存储一个额外的颜色位,用于确保树的平衡性。在红黑树中,节点的颜色可以是红色或黑色。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。

1. 2 红黑树的性质
红黑树通过以下性质来保持树的平衡:
-
每个节点是红色或黑色。
-
根节点是黑色。
-
每个叶子节点(NIL节点)是黑色。
ps:NIL节点不是传统意义上的叶子节点,而是指空节点,是用来方便我们来数路径的。

-
如果一个节点是红色,则它的两个子节点都是黑色(不能出现连续的红色节点)。
-
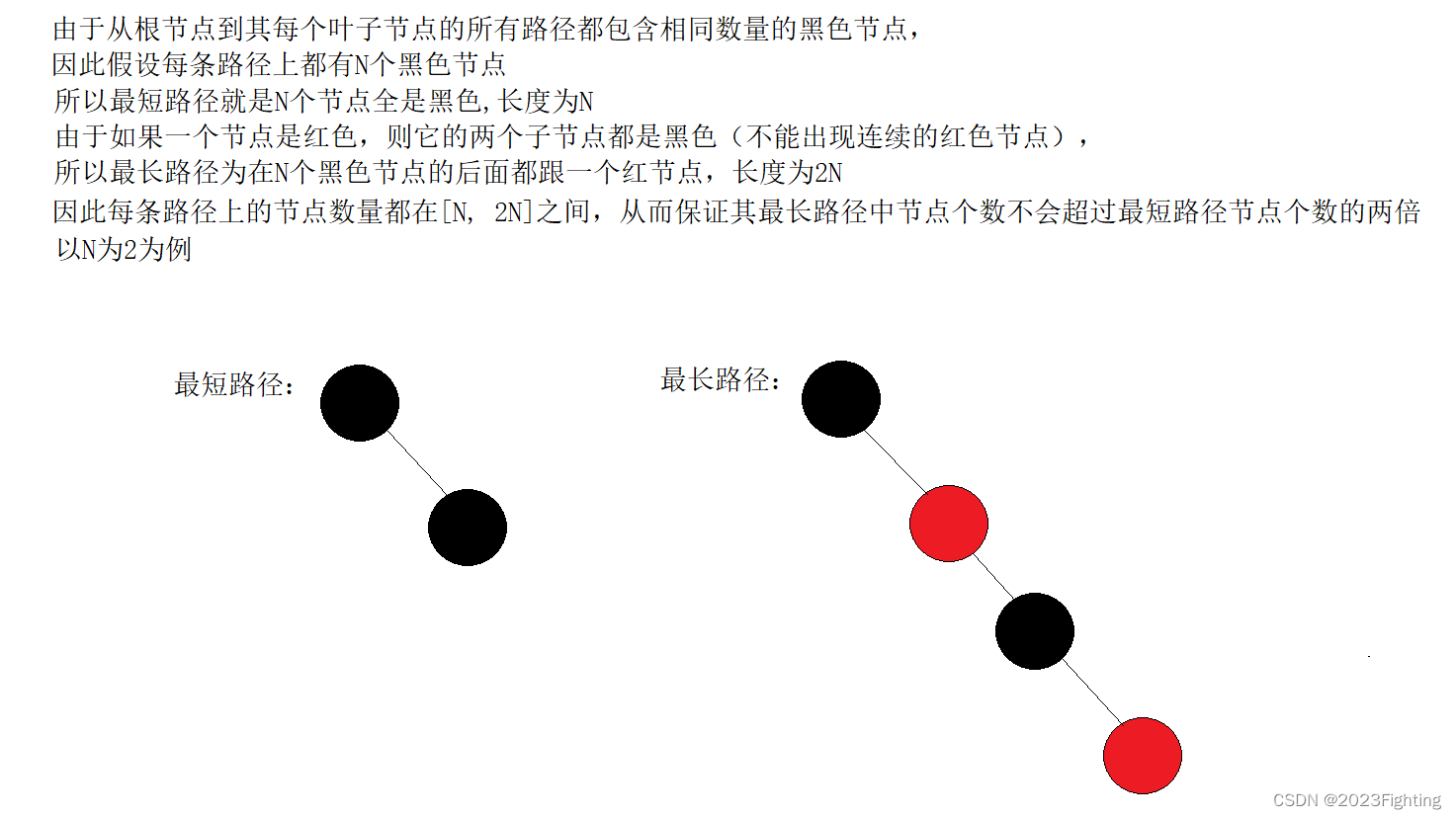
从根节点到其每个叶子节点的所有路径都包含相同数量的黑色节点。
为什么满足上面的性质,红黑树就能保证其最长路径中节点个数不会超过最短路径节点个数的两倍?
分析如下:
2. 红黑树节点的定义
TreeNode成员的几点解释:
- 枚举类型 Color 用于表示红黑树节点的颜色。红黑树节点只能是红色或黑色。
- TreeNode 是一个模板结构体,用于存储红黑树节点的信息。
_left 指向左孩子节点,_right 指向右孩子节点,_parent 指向父节点。
_kv 存储节点的键值对,类型为 pair<K, V>,其中 K 是键的类型,V 是值的类型。
_col 存储节点的颜色,类型为 Color。
构造函数初始化节点的左孩子、右孩子和父节点为空指针,键值对通过参数传递进来,并将节点颜色初始化为红色(新插入的节点默认是红色)。
enum Color
{RED,BLACK
};
template<class K, class V>
struct TreeNode
{TreeNode* _left; // 左孩子节点TreeNode* _right;// 右孩子节点TreeNode* _parent;// 父节点pair<K, V> _kv;// 存储键值对Color _col; // 节点颜色// 构造函数TreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED)// 新插入的节点初始为红色{}
};
3. 红黑树的插入
红黑树就是在二叉搜索树的基础上增加了节点的颜色来控制平衡,因此红黑树也可以看成是二叉搜索树。那么红黑树的插入过程可以分为两步:
- 按照二叉搜索树的方式插入新节点。
- 检测新节点插入后,红黑树的性质是否造到破坏。
具体操作步骤如下:
3.1 按照二叉搜索的树规则插入新节点
具体操作过程参考之前写的文章,这里就不在赘述,详情参考之前写的这篇文章:搜索二叉树,这里直接给出插入新节点的具体代码。
bool insert(const pair<K, V>& kv)
{//空树if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//找插入位置Node* cur = _root;Node* parent = nullptr;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}//插入cur = new Node(kv);if (kv.first > parent->_kv.first){parent->_right = cur;cur->_parent = parent;}else{cur->_parent = parent;parent->_left = cur;}
}
3.2 检测新节点插入后,红黑树的性质是否造到破坏
这里涉及的旋转操作参考之前写的文章AVL树(C++),里面详细介绍了旋转操作,这里就不在赘述。
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;
注意:下面图片中的树有可能是一颗完整的树,也有可能是一颗局部的子树。

但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树分情况来讨论:
ps:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点。
- 情况一: cur为红,p为红,g为黑,u存在且为红。

ps:cur可能是新插入的节点,也有可能是在下面插入节点,不断往上调整,使得cur的颜色变红。
解决方式:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。

ps:如果g是根节点,调整完成后,需要将g改为黑色;
如果g是子树,g一定有双亲,且g的双亲如果是红色,需要继续向上调整。

- 情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑
解决方式:
cur是p的左孩子,以g为旋转点右单旋,g变红,p变黑,调整结束,无需向上调整;
cur是p的右孩子,先以p为旋转点左单旋,再以g为旋转点右单旋,g变红,p变黑,调整结束,无需向上调整。

1. 如果u节点不存在,则cur一定是新插入节点,因为如果cur不是新插入节点则cur和p一定有一个节点的颜色是黑色,就不满足性质4:每条路径黑色节点个数相同。

2. 如果u节点存在,则其一定是黑色的,那么cur节点原来的颜色一定是黑色的现在看到其是红色的原因是因为cur的子树在调整的过程中将cur节点的颜色由黑色改成红色。

p有可能是g的右孩子,这种情况下旋转操作与上面的情况相反,变色操作还是一样的,这里就不在赘述了。
如下图:

检测新节点插入后,红黑树的性质是否造到破坏的具体代码如下:
//插入以后判断是否满足红黑树的规则
//不满足则调整
while (parent && parent->_col == RED)
{Node* grandfather = parent->_parent;//p是g的左孩子if (parent == grandfather->_left){Node* uncle = grandfather->_right;//u存在且为红if (uncle && uncle->_col == RED){//变色+向上调整parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = grandfather->_parent;}else{//不存在或者存在且为黑//旋转+变色//cur 是p的左 以g为旋转点右单旋if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//cur 是p的右 先以p为旋转点左单旋,再以g为旋转点右单旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else//p是g的右孩子{Node* uncle = grandfather->_left;//u存在且为红if (uncle && uncle->_col == RED){//变色+向上调整parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = grandfather->_parent;}else{//不存在或者存在且为黑//旋转+变色//cur 是p的右 以g为旋转点左单旋if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//cur 是p的左 先以p为旋转点右单旋,再以g为旋转点左单旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}
}
_root->_col = BLACK;
4.红黑树的删除
红黑树的删除和AVL树一样不做深入研究,实现红黑树的插入已经足够帮助我们来了解其是如何控制平衡的,关于红黑树的删除有兴趣的可参考:《算法导论》或者《STL源码剖析》。
5.红黑树的验证
红黑树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证红黑树,可以分两步:
- 检测其是否满足二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树。
代码如下:
void _InOrder(Node* root)
{if (root == nullptr) return;_InOrder(root->_left);cout << root->_kv.first << ' ';_InOrder(root->_right);
}
void InOrder()
{_InOrder(_root);cout << endl;
}
- 检测其是否满足红黑树的性质
不能出现连续的红色节点;每条路径上的黑色节点数量相同。
bool _IsRbTree(Node* root, int blacknum, int num)
{if (root == nullptr){//判断当前路径和最左路径上的黑色节点数量是否相同if (blacknum != num)return false;return true;}//当前节点为黑色,当前路径上的黑色节点数量加1if (root->_col == BLACK) num++;Node* parent = root->_parent;//判断是否出现连续的红色节点if (root->_col == RED && parent->_col == RED){cout << "出现连续的红色节点";return false;}//递归去判断其左右子树是否满足性质return _IsRbTree(root->_left, blacknum, num)&& _IsRbTree(root->_right, blacknum, num);
}
bool IsRbTree()
{//空树是红黑树if (_root == nullptr) return true;if (_root->_col == RED) return false;//检查根节点的颜色//统计最左路径黑色节点的数量,以其为参考值,去判断每条路径上的黑色节点数量是否相同int blacknum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){blacknum++;}cur = cur->_left;}return _IsRbTree(_root, blacknum, 0);
}
验证用例:
常规场景1 :{16, 3, 7, 11, 9, 26, 18, 14, 15}。

特殊场景2:{4, 2, 6, 1, 3, 5, 15, 7, 16, 14}。

场景三:随机生成N个数字插入验证,这里给出代码,有兴趣的可以自己去测试一下。
int main()
{const int N = 1000;srand((unsigned int)time(nullptr));RBTree<int, int> rbTree;for (int i = 0; i < N; ++i){int num = rand() + i;rbTree.insert(make_pair(num, num));}//rbTree.InOrder();cout << rbTree.IsRbTree();return 0;
}
6.源码
#include <iostream>
using namespace std;
enum Color
{RED,BLACK
};
template<class K, class V>
struct TreeNode
{TreeNode* _left;TreeNode* _right;TreeNode* _parent;pair<K, V> _kv;Color _col;TreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED){}
};template<class K, class V>
class RBTree
{typedef TreeNode<K, V> Node;
public:bool insert(const pair<K, V>& kv){//空树if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//找插入位置Node* cur = _root;Node* parent = nullptr;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}//插入cur = new Node(kv);if (kv.first > parent->_kv.first){parent->_right = cur;cur->_parent = parent;}else{cur->_parent = parent;parent->_left = cur;}//插入以后判断是否满足红黑树的规则//不满足则调整while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = grandfather->_parent;}else{if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = grandfather->_parent;}else{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}void InOrder(){_InOrder(_root);cout << endl;}bool IsRbTree(){if (_root == nullptr) return true;if (_root->_col == RED) return false;int blacknum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){blacknum++;}cur = cur->_left;}return _IsRbTree(_root, blacknum, 0);}
private:bool _IsRbTree(Node* root, int blacknum, int num){if (root == nullptr){if (blacknum != num)return false;return true;}if (root->_col == BLACK) num++;Node* parent = root->_parent;if (root->_col == RED && parent->_col == RED){cout << "出现连续的红色节点";return false;}return _IsRbTree(root->_left, blacknum, num)&& _IsRbTree(root->_right, blacknum, num);}void _InOrder(Node* root){if (root == nullptr) return;_InOrder(root->_left);cout << root->_kv.first << ' ';_InOrder(root->_right);}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;//旋转,sub的右子树做parent的左子树//parent做subL的右子树parent->_right = subRL;if (subRL){subRL->_parent = parent;}Node* pParent = parent->_parent;subR->_left = parent;parent->_parent = subR;//parent为根节点,需要将根节点更新为subR if (parent == _root){_root = subR;subR->_parent = nullptr;}else{//更新subR的父节点指针if (subR->_kv.first > pParent->_kv.first){pParent->_right = subR;}else{pParent->_left = subR;}subR->_parent = pParent;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* pParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (subL->_kv.first > pParent->_kv.first){pParent->_right = subL;}else{pParent->_left = subL;}subL->_parent = pParent;}}
private:Node* _root = nullptr;
};#include "RBTree.h"
int main()
{RBTree<int, int> rbTree;int nums[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto e : nums){rbTree.insert(make_pair(e, e));}rbTree.InOrder();cout << rbTree.IsRbTree() << endl;return 0;
}
至此,本片文章就结束了,若本篇内容对您有所帮助,请三连点赞,关注,收藏支持下。
创作不易,白嫖不好,各位的支持和认可,就是我创作的最大动力,我们下篇文章见!
如果本篇博客有任何错误,请批评指教,不胜感激 !!!

相关文章:

红黑树(C++)
文章目录 写在前面1. 红黑树的概念及性质1. 1 红黑树的概念1. 2 红黑树的性质 2. 红黑树节点的定义3. 红黑树的插入3.1 按照二叉搜索的树规则插入新节点3.2 检测新节点插入后,红黑树的性质是否造到破坏 4.红黑树的删除5.红黑树的验证6.源码 写在前面 在上篇文章中&…...
PyCharm设置不默认打开上次的项目
第一步 第二步 第三步 测试...
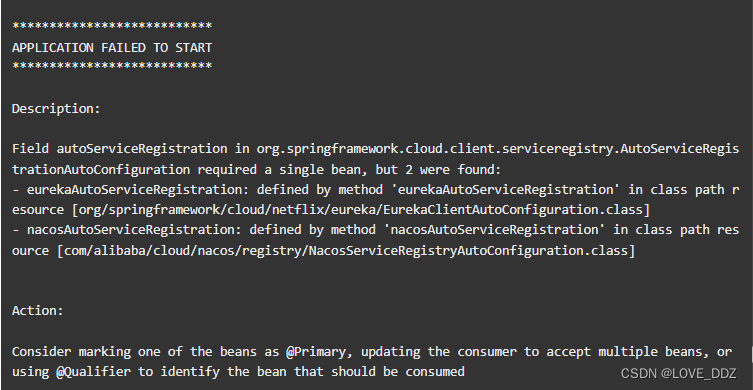
Eureka到Nacos迁移实战:解决配置冲突与启动异常
问题:Eureka到Nacos迁移实战:解决配置冲突与启动异常 在进行微服务架构升级,特别是注册中心从Eureka转向Nacos的过程中,我遇到了一个典型的技术挑战。目标是为了减少因配置变更导致的服务重启频率,我决定拥抱Nacos以其…...

k8s 小技巧: 查看 Pod 上运行的容器
目录 1. 示例 Pod 的定义文件2. kubectl describe pod(推荐)3. kubectl get pod3.1 json 格式3.2 yaml 格式 4. 其他操作 1. 示例 Pod 的定义文件 # 文章中所用 pod 的 yaml 定义文件, multi-container.yaml apiVersion: v1 kind: Pod metad…...

【Git】基础操作
初识Git 版本控制的方式: 集中式版本控制工具:版本库是集中存放在中央服务器的,team里每个人work时从中央服务器下载代码,是必须联网才能工作,局域网或者互联网。个人修改之后要提交到中央版本库 例如:SVM和…...
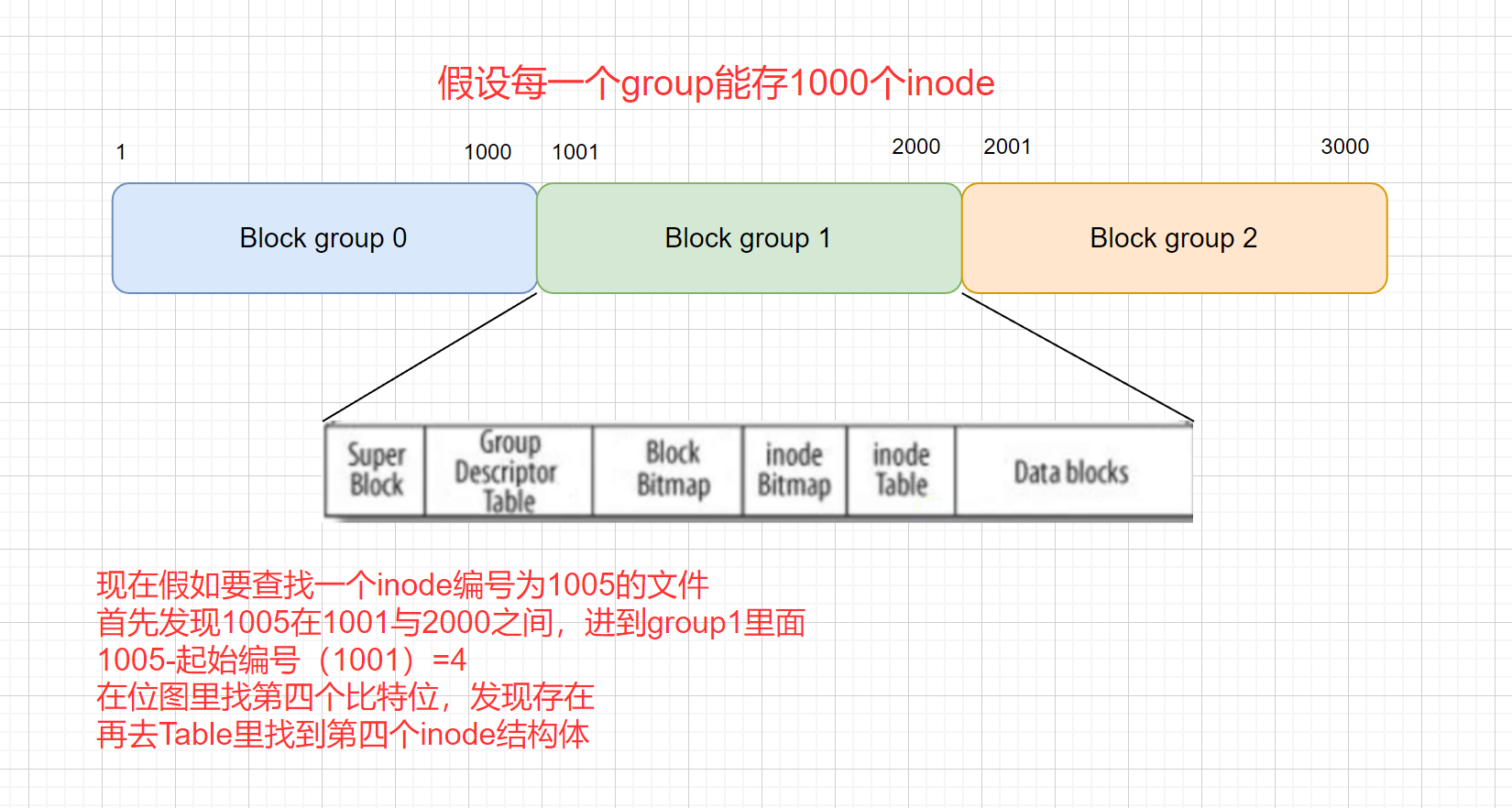
Linux:基础IO(二.缓冲区、模拟一下缓冲区、详细讲解文件系统)
上次介绍了:Linux:基础IO(一.C语言文件接口与系统调用、默认打开的文件流、详解文件描述符与dup2系统调用) 文章目录 1.缓冲区1.1概念1.2作用与意义 2.语言级别的缓冲区2.1刷新策略2.2具体在哪里2.3支持格式化 3.自己来模拟一下缓…...

事件传播机制 与 责任链模式
1、基本概念 责任链模式(Chain of Responsibility Pattern)是一种行为型设计模式,将请求沿着处理链传递,直到有一个对象能够处理为止。 2、实现的模块有: Handler(处理者):定义一个…...
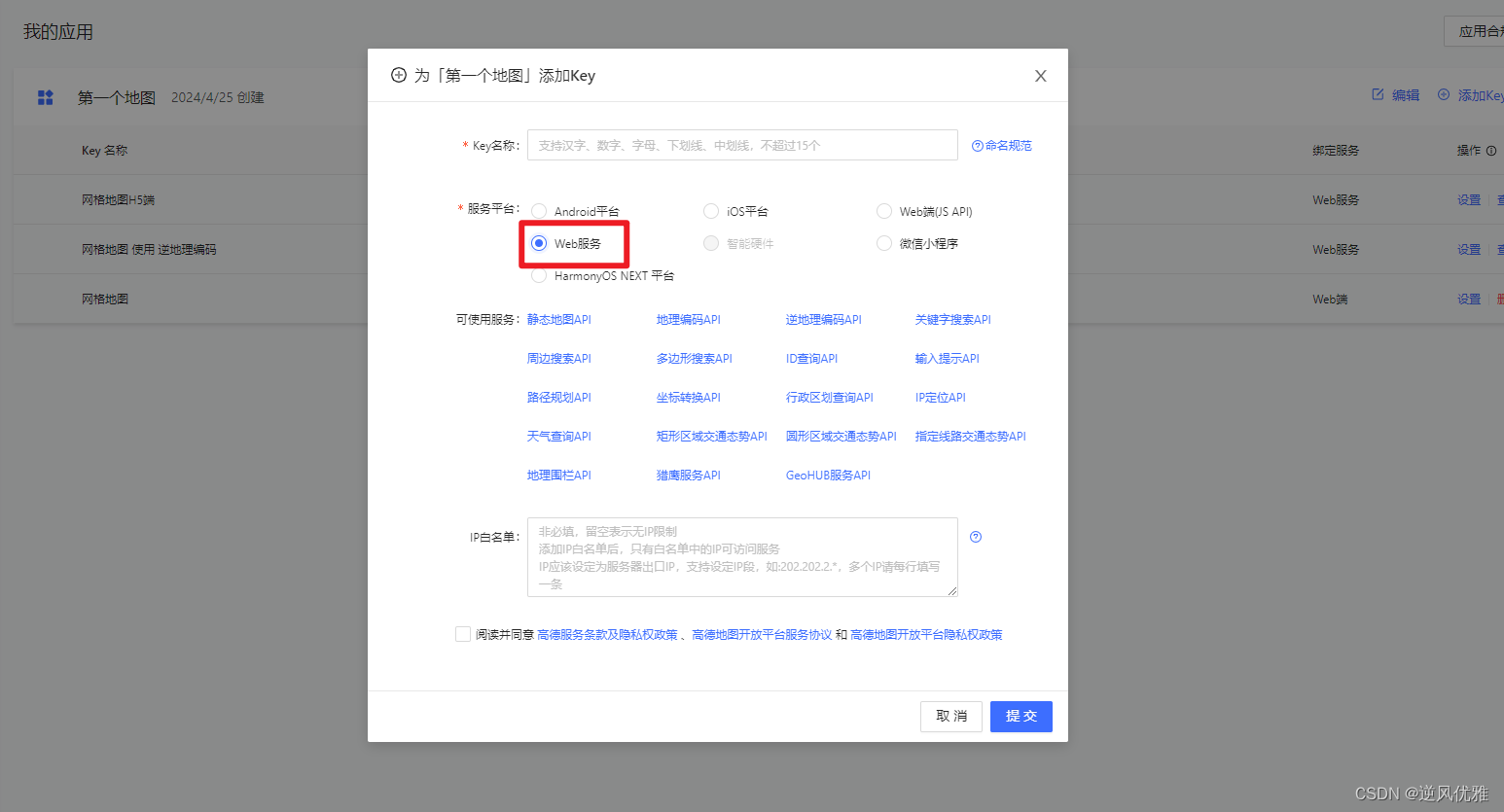
uniapp 展示地图,并获取当前位置信息(精确位置)
使用uniapp 提供的map标签 <map :keymapIndex class"container" :latitude"latitude" :longitude"longitude" ></map> 页面初始化的时候,获取当前的位置信息 created() {let that thisuni.getLocation({type: gcj02…...
)
Autosar实践——诊断配置(DaVinci Configuration)
文章目录 一、制作诊断数据库文件(cdd文件)二、导入诊断数据库文件并修复模块生成的问题三、创建SWC CS接口Service Ports四、创建Service Runnable五、关联SWC和DCM/DEM模块六、RTE代码编写22服务2E服务31服务DTC Set/Get关联文章列表: Autosar-软件架构 Autosar诊断-简介和…...
植物大战僵尸杂交版全新版v2.1解决全屏问题
文章目录 🚋一、植物大战僵尸杂交版❤️1. 游戏介绍💥2. 如何下载《植物大战僵尸杂交版》 🚀二、解决最新2.1版的全屏问题🌈三、画质增强以及减少闪退 🚋一、植物大战僵尸杂交版 《植物大战僵尸杂交版》是一款在原版《…...

【code-server】Code-Server 安装部署
Code-Server 安装部署 1.环境准备 可以参考 https://coder.com/docs/code-server/install code-server的安装流程进行安装,主机环境是 Centos7 建议使用 docker 方式进行安装,可能会出现如下报错,需要升级 GNC 的版本,由于影响较…...

博客摘录「 YOLOv5模型剪枝压缩」2024年5月11日
添加L1正则来约束BN层系数 语义边缘检测和语义分割的关系调研结果为,语义信息可以用来增强语义分割的效果,也有一定的优点和采用理由,但此类论文的数量并不是很多,语义分割的多数方法还是使用深度学习直接做像素分类。在对比两者…...

HttpSecurity
这是Spring Security提供的配置类, 用户保护基于HTTP的请求 ,通过HttpSecurity可以设置各种安全设置{认证,授权,CSRF保护,会话管理,异常处理} 主要功能和配置: 1.认证配置: 配置登录和登出功能,指定登录页面、登录处理 URL、成功和失败处理器等。配置认证方式,如表单登录、…...

Mysql union语句
开源项目SDK:https://github.com/mingyang66/spring-parent 个人文档:https://mingyang66.github.io/raccoon-docs/#/ mysql union操作符用于连接两个以上的select语句的结果组合到一个结果集,并去除重复的行,每个select语句的雷叔…...

MySQL之高级特性(四)
高级特性 查询缓存 什么情况下查询缓存能发挥作用 并不是什么情况下查询缓存都会提高系统性能的。缓存和失效都会带来额外的消耗,所以只有当缓存带来的资源节约大于本身的资源消耗时才会给系统带来性能提升。这跟具体的服务器压力模型有关。理论上,可…...

roles安装wordpress
debug模块 1.如何查看ansible-playbook执行过程中产生的具体信息 vim test3.yaml --- - hosts: allremote_user: roottasks:- name: lsshell: ls /rootregister: var_stdout # register:将var_stdout注册为变量- name: debugdebug:var: var_stdout # 查看所有的输出信息#var…...

【Python高级编程】饼状图中autopct和startangle用来做什么的
autopct 设置饼状图中每个扇区的百分比标签。接受一个格式字符串,用于指定如何格式化标签。默认值为 %.1f%%,表示保留一位小数的百分比格式。可以设置为 None 以禁用百分比标签。 startangle 设置饼状图中第一个扇区的起始角度。角度以顺时针方向从 3…...

【ARM Coresight Debug 系列 -- ARMv8/v9 Watchpoint 软件实现地址监控详细介绍】
请阅读【嵌入式开发学习必备专栏 】 文章目录 ARMv8/v9 Watchpoint exceptionsWatchpoint 配置信息读取Execution conditionsWatchpoint data address comparisonsSize of the data accessWatchpoint 软件配置流程Watchpoint Type 使用介绍WT, Bit [20]: Watchpoint TypeLBN, B…...

jvm工具-jps、jstat、jmap、jstack
一、jps jps -v 【输出进程启动参数】 [rootVM-8-2-centos ~]# jps -v 12401 Jps -Dapplication.home/usr/local/jdk1.8.0_241 -Xms8m 16964 jar 其他参考 Java八股文必看,入门到深入理解jvm虚拟机之基础故障指令【jps,jstate...】-CSDN博客 二、j…...
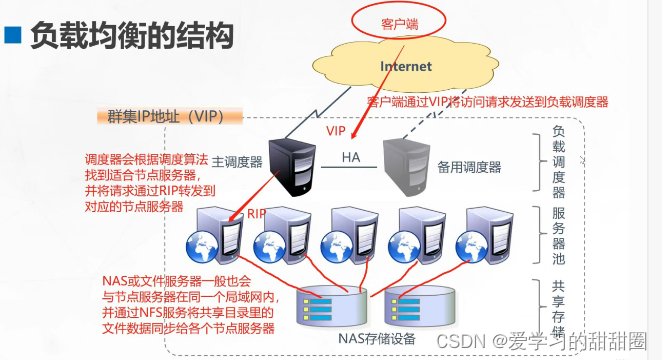
LVS负载均衡群集+NAT部署
目录 一、企业群集应用概述 1.1 群集的含义 1.2 企业群集分类 二、负载均衡群集架构和工作模式 2.1负载均衡的结构 2.2负载均衡群集工作模式分析 三、LVS虚拟服务器 3.1Linux Virtual Server 3.2LVS必要的工具 3.3LVS的负载调度算法 一、企业群集应用概述 1.1 群集的…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

算法刷题-回溯
今天给大家分享的还是一道关于dfs回溯的问题,对于这类问题大家还是要多刷和总结,总体难度还是偏大。 对于回溯问题有几个关键点: 1.首先对于这类回溯可以节点可以随机选择的问题,要做mian函数中循环调用dfs(i&#x…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...

基于Java项目的Karate API测试
Karate 实现了可以只编写Feature 文件进行测试,但是对于熟悉Java语言的开发或是测试人员,可以通过编程方式集成 Karate 丰富的自动化和数据断言功能。 本篇快速介绍在Java Maven项目中编写和运行测试的示例。 创建Maven项目 最简单的创建项目的方式就是创建一个目录,里面…...
