【动态规划】| 路径问题之最小路径和 力扣64
🎗️ 主页:小夜时雨
🎗️专栏:动态规划
🎗️如何活着,是我找寻的方向
目录
- 1. 题目解析
- 2. 代码
1. 题目解析
题目链接: https://leetcode.cn/problems/minimum-path-sum/description/

这道题目和之前一道题 不同路径1力扣62: https://leetcode.cn/problems/unique-paths/description/ 有相似的地方, 建议先去看看那道题整理一下思路, 会简单一些.
通常动态规划的题目有五个大步骤进行解析, 接下来一一来进行分析.
1. 状态表示
动态规划的重点是状态表示, 我们通过状态表示才可以写出正确的状态转移方程, 状态表示我们通常都是根据 经验+题目 要求来进行定义的.
比如本道题又是一个二维的矩阵, 那么依旧可以定义我们的状态表示为
dp[i][j]: 表示到达 (i, j) 这个位置时, 路径上的数字总和为最小
2. 状态转移方程
- 根据题目要求, 假如我们走到了 (i,j) 位置时, 我们可以从上面往下走或者是从左面往右走, 即是从 (i-1, j) 或者 (i, j-1) 往 (i, j) 的位置走。
- 根据状态表示, dp[i][j] 的大小可以由两部分组成, 问的是路径总和为最小, 那么共有两条不同的路径: 从左往右走或者从上往下走,求的应该是这二者中的最小值。
- 从 (0, 0) 走到 (i-1, j) 的最小路径总和假设为 X , 那么从 (0, 0) 走到 (i, j) 的最小路径总和就是 X + nums[i][j], 注意要加上 (i,j)位置的数字。
- 正好所对应的就是 dp[i - 1][j] 所表示的含义. 同理 dp[i][j - 1] 也是. 那么状态转移方程应如下表示:
dp[i][j] = Math.min(dp[i - 1][j],dp[i][j - 1]) + nums[i][j]
- 但是有一个细节问题, 这里和不同路径1 不同的是, 这里需要用到原数组,我们通常也是采取多加一行一列的方式来避免出现 dp 表越界的情况, 所以要注意映射关系。
- 即是遍历 dp 表填表的过程中的 (i, j)对应原数组的值是 nums[i- 1][j - 1] 要注意,后面还会再强调一遍。
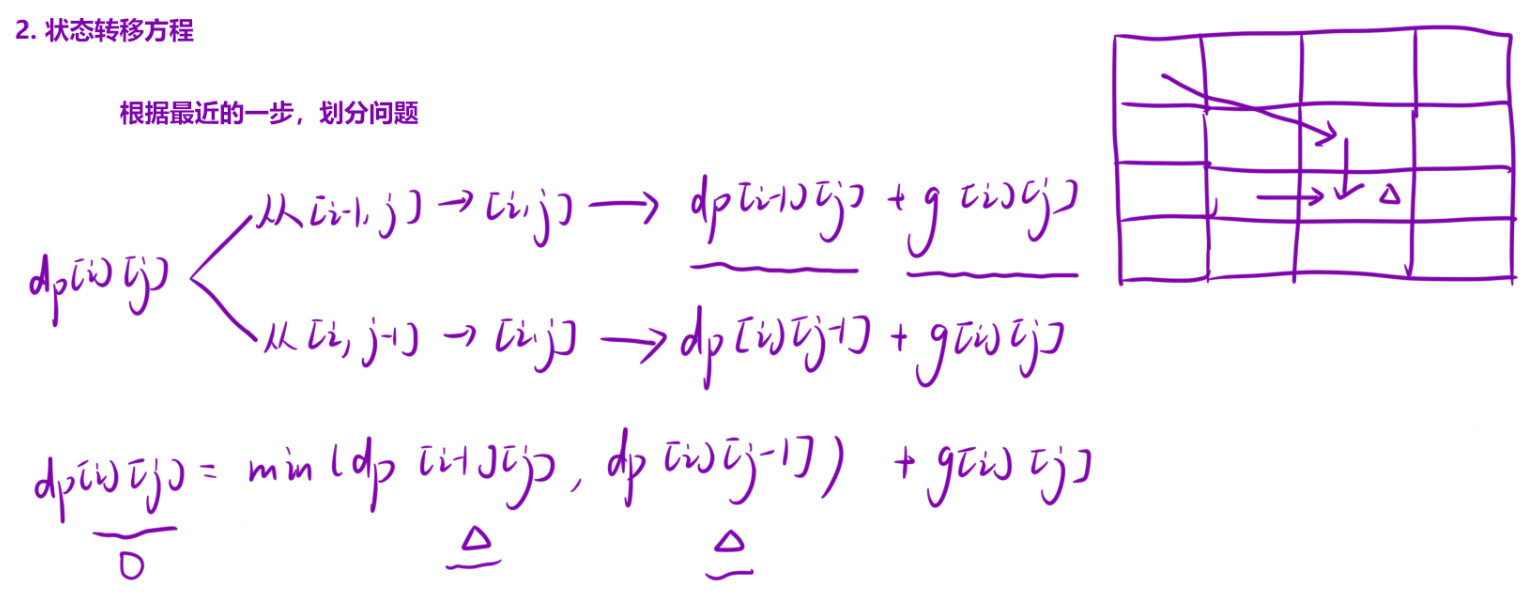
3. 初始化
细节问题: 观察状态转移方程可知, 有可能会有越界的风险, 此处我们依旧采取一种多加一行一列的方式来进行初始化.多加一行一列要保证两点:
- 虚拟节点的值要保证后面的dp 表里的值是正确的
- 要注意下标的映射关系. 因为我们是多加了一行一列, 所以对应到原始数组就应该行列要减一. (此处用到了原数组, 所以要有这个映射关系)
注意 :
这道题的初始化和前两道题有些许不同
- 原本的dp[0][0] 最小的路径和就是本身自己, 也就是 dp[0][0] = nums[0][0]. 因为我们多加了一行一列, 所以变成了 dp[1][1] = nums[0][0].
- 观察下图我们发现,填写 dp[1][1] 的时候需要用到左边和上边值, 因为求的是二者中的最小值, 为了不干扰结果, 设置为0即可。
- 看下图,但是填写 dp[1][2] 的时候,需要用到上面的值 dp[0][2] 和 dp[1][1] 作比较求最小值,倘如是dp[1][2] 还是默认初始化为 0 的话, 就会影响结果,使dp[1][2] = dp[0][2] + nums[0][1], 导致错误了.
- dp[1][2] 本该是只有一条路径, 那就是用到 (1,1)走到(1,2),就应该是 dp[1][2] = dp[1][1] + nums[0][1]. 观察结果,让 dp[0][2] 是一个非常大的数字,不影响结果即可。此处通常我们设置为整数最大值或者 0x3f3f3f3f.
看图更容易理解
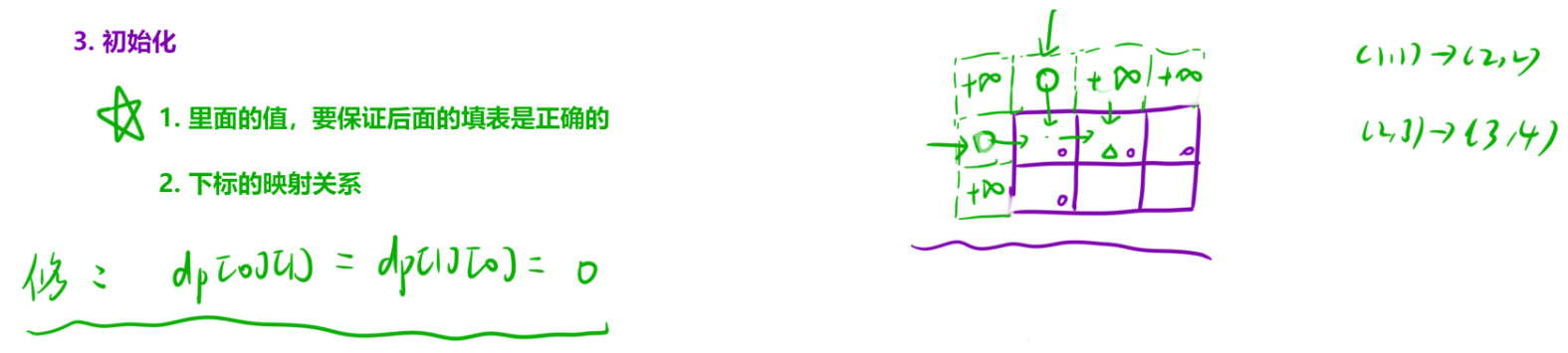
4. 填表顺序
观察可知, 填 (i, j) 的值的时候需要用到上一行和左边的值. 所以填表顺序是 从上往下, 从左往右.
5. 返回值
根据题目的要求, 要到达(m, n) 最小路径和是多少, 正好对应 dp[m][n] 的表示. 所以返回 dp[m][n] 即可.
2. 代码
动态规划的代码编写一般都是分为 4 个步骤进行:
- 创建 dp 表
- 初始化
- 填表
- 返回值
// 动态规划// 是不同路径1 的小幅改动版版: https://leetcode.cn/problems/unique-paths/public int uniquePathsWithObstacles(int[][] ob) {// 1.创建 dp表// 2.初始化// 3.填表// 4.返回值// 动态规划 这里的是二维, 所以时空都是O(M*N)int m = ob.length, n = ob[0].length;int[][] dp = new int[m + 1][n + 1];// dp[1][1] = 1;dp[0][1] = 1;// 做好映射关系, 原数组的(0,0) 对应dp表中的(1,1)// 这里填的是 dp 表, 所以建议从(1,1) 开始, 也就是dp表多加了一行一列// 如果是障碍的话, 就直接忽略, 默认就是 0, 也就是表示到不了for(int i = 1; i <= m; i++) { // 从上往下每一行for(int j = 1; j <= n; j++) { // 从左往右每一列if(ob[i - 1][j - 1] == 0) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}}return dp[m][n];}
🎗️🎗️🎗️ 好啦,到这里有关本题的分享就没了,如果感觉做的还不错的话可以点个赞,关注一下,你的支持就是我继续下去的动力,我们下期再见,拜了个拜~ ☆*: .。. o(≧▽≦)o .。.:*☆
相关文章:
【动态规划】| 路径问题之最小路径和 力扣64
🎗️ 主页:小夜时雨 🎗️专栏:动态规划 🎗️如何活着,是我找寻的方向 目录 1. 题目解析2. 代码 1. 题目解析 题目链接: https://leetcode.cn/problems/minimum-path-sum/description/ 这道题目和之前一道…...

如何在vector中插入和删除元素?
在C的std::vector中插入和删除元素通常使用其成员函数来完成。以下是如何在std::vector中插入和删除元素的示例: 插入元素 在末尾插入元素:使用push_back函数。 cpp复制代码 #include <vector> int main() { std::vector<int> v; v.push_…...
独具韵味的移动端 UI 风格
独具韵味的移动端 UI 风格...

【SpringBoot】SpringBoot:构建实时聊天应用
文章目录 引言项目初始化添加依赖 配置WebSocket创建WebSocket配置类创建WebSocket处理器 创建前端页面创建聊天页面 测试与部署示例:编写单元测试 部署扩展功能用户身份验证消息持久化群组聊天 结论 引言 随着实时通信技术的快速发展,聊天应用在现代We…...

基于Matlab的车牌识别停车场出入库计时计费管理系统(含GUI界面)【W6】
简介: 在当今城市化进程加快的环境下,停车管理成为了一个日益重要和复杂的问题。城市中的停车资源有限,如何高效利用和管理这些资源,不仅关乎市民出行便利性,也涉及到城市交通拥堵、环境污染等诸多问题的解决。 传统的…...

大众点评js逆向过程(未完)
相关链接 1、控制流平坦化进行AST 解析 AST网址 2、JS进制转换(Function.prototype.call) 1、断点调试mtgsig参数 这里mtgsig已经被拼到url中 2、进入后mtgsig已经计算完, ir he(this[b(4326)], !1), 就是加密函数 
web前端如何设置单元格:深入解析与实用技巧
web前端如何设置单元格:深入解析与实用技巧 在web前端开发中,设置单元格是一个常见且重要的任务。无论是构建数据表格、表单还是其他界面元素,都需要对单元格进行精确的设置和样式调整。那么,web前端究竟如何设置单元格呢&#x…...

龙迅LT9611UXC 2 PORT MIPIDSI/CSI转HDMI 2.1,支持音频IIS/SPDIF输入,支持标准4K60HZ输出
龙迅LT9611UXC描述: LT9611UXC是一个高性能的MIPI DSI/CSI到HDMI2.0转换器。MIPI DSI/CSI输入具有可配置的单端口或双端口,1高速时钟通道和1~4高速数据通道,最大2Gbps/通道,可支持高达16Gbps的总带宽。LT9611UXC支持突发模式DSI视…...

红黑树(C++)
文章目录 写在前面1. 红黑树的概念及性质1. 1 红黑树的概念1. 2 红黑树的性质 2. 红黑树节点的定义3. 红黑树的插入3.1 按照二叉搜索的树规则插入新节点3.2 检测新节点插入后,红黑树的性质是否造到破坏 4.红黑树的删除5.红黑树的验证6.源码 写在前面 在上篇文章中&…...
PyCharm设置不默认打开上次的项目
第一步 第二步 第三步 测试...
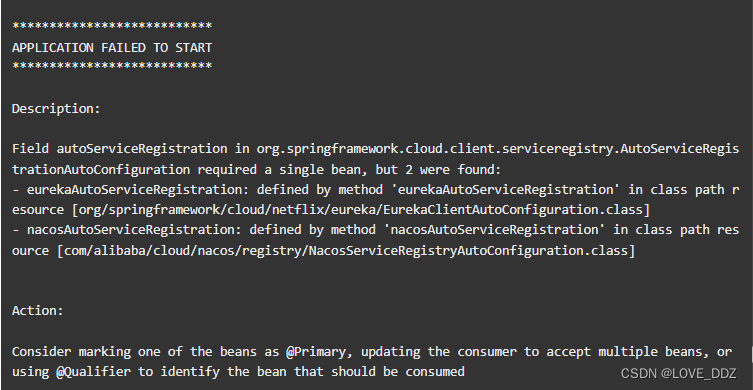
Eureka到Nacos迁移实战:解决配置冲突与启动异常
问题:Eureka到Nacos迁移实战:解决配置冲突与启动异常 在进行微服务架构升级,特别是注册中心从Eureka转向Nacos的过程中,我遇到了一个典型的技术挑战。目标是为了减少因配置变更导致的服务重启频率,我决定拥抱Nacos以其…...

k8s 小技巧: 查看 Pod 上运行的容器
目录 1. 示例 Pod 的定义文件2. kubectl describe pod(推荐)3. kubectl get pod3.1 json 格式3.2 yaml 格式 4. 其他操作 1. 示例 Pod 的定义文件 # 文章中所用 pod 的 yaml 定义文件, multi-container.yaml apiVersion: v1 kind: Pod metad…...

【Git】基础操作
初识Git 版本控制的方式: 集中式版本控制工具:版本库是集中存放在中央服务器的,team里每个人work时从中央服务器下载代码,是必须联网才能工作,局域网或者互联网。个人修改之后要提交到中央版本库 例如:SVM和…...
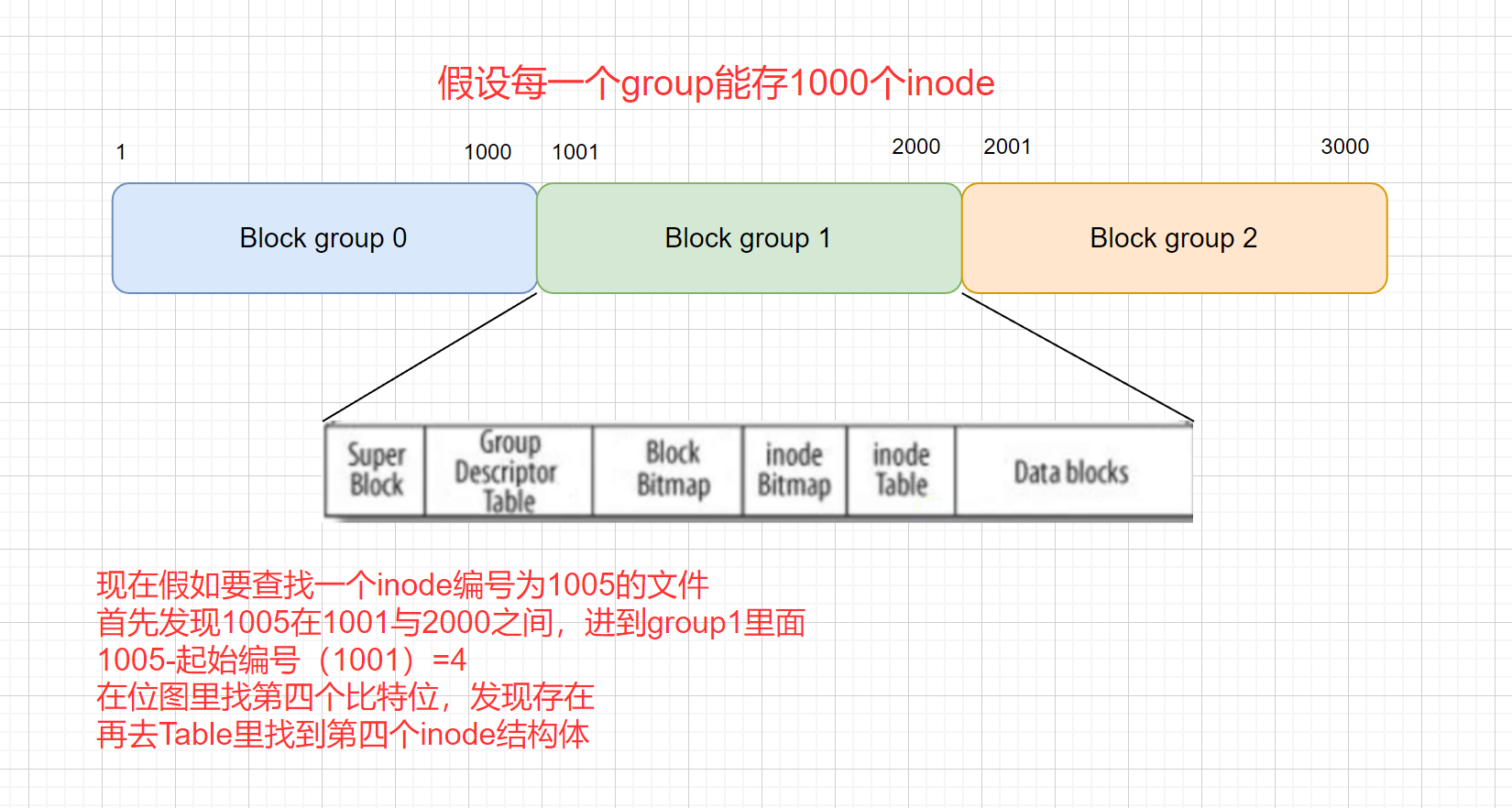
Linux:基础IO(二.缓冲区、模拟一下缓冲区、详细讲解文件系统)
上次介绍了:Linux:基础IO(一.C语言文件接口与系统调用、默认打开的文件流、详解文件描述符与dup2系统调用) 文章目录 1.缓冲区1.1概念1.2作用与意义 2.语言级别的缓冲区2.1刷新策略2.2具体在哪里2.3支持格式化 3.自己来模拟一下缓…...

事件传播机制 与 责任链模式
1、基本概念 责任链模式(Chain of Responsibility Pattern)是一种行为型设计模式,将请求沿着处理链传递,直到有一个对象能够处理为止。 2、实现的模块有: Handler(处理者):定义一个…...
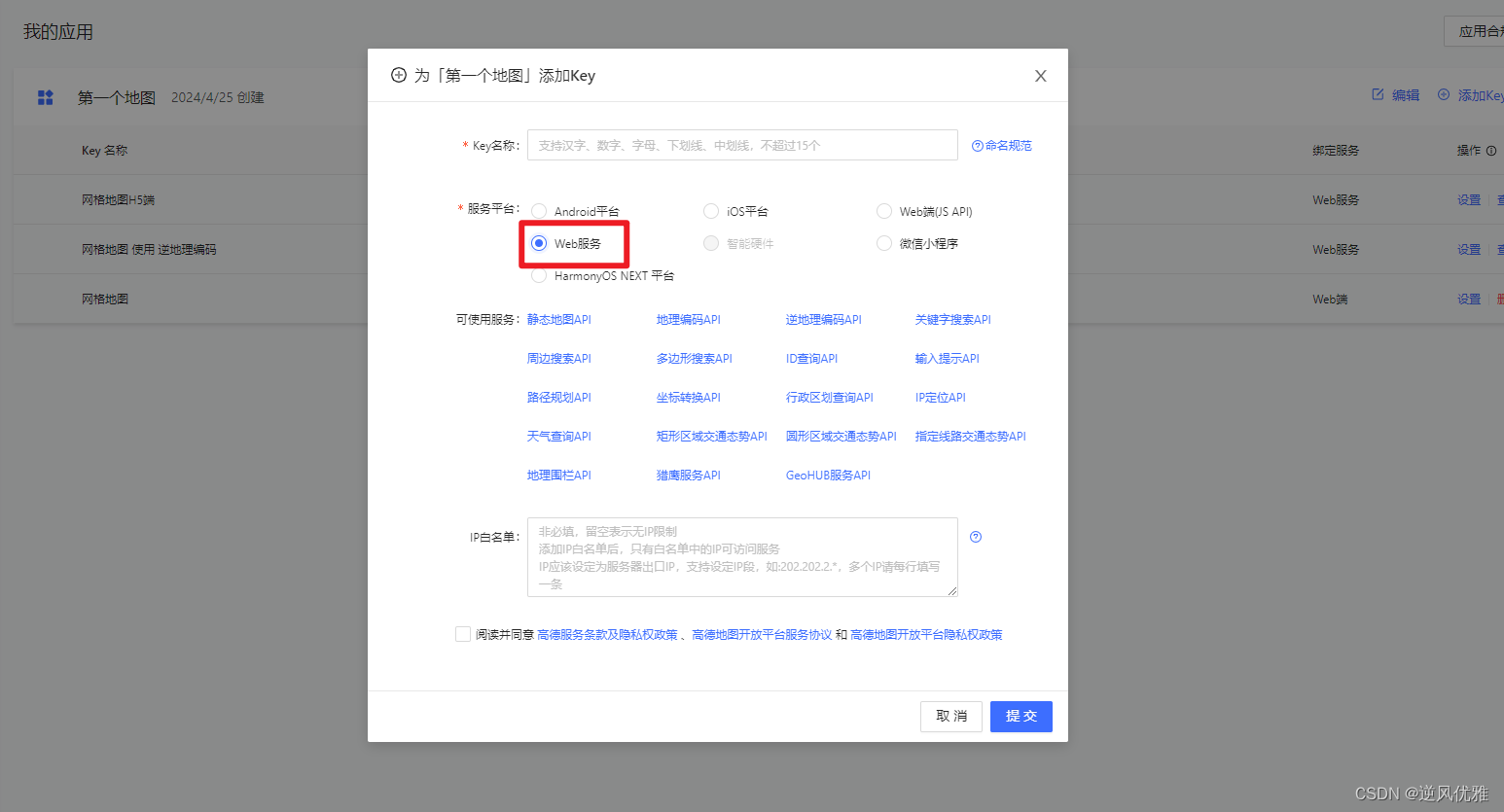
uniapp 展示地图,并获取当前位置信息(精确位置)
使用uniapp 提供的map标签 <map :keymapIndex class"container" :latitude"latitude" :longitude"longitude" ></map> 页面初始化的时候,获取当前的位置信息 created() {let that thisuni.getLocation({type: gcj02…...
)
Autosar实践——诊断配置(DaVinci Configuration)
文章目录 一、制作诊断数据库文件(cdd文件)二、导入诊断数据库文件并修复模块生成的问题三、创建SWC CS接口Service Ports四、创建Service Runnable五、关联SWC和DCM/DEM模块六、RTE代码编写22服务2E服务31服务DTC Set/Get关联文章列表: Autosar-软件架构 Autosar诊断-简介和…...
植物大战僵尸杂交版全新版v2.1解决全屏问题
文章目录 🚋一、植物大战僵尸杂交版❤️1. 游戏介绍💥2. 如何下载《植物大战僵尸杂交版》 🚀二、解决最新2.1版的全屏问题🌈三、画质增强以及减少闪退 🚋一、植物大战僵尸杂交版 《植物大战僵尸杂交版》是一款在原版《…...

【code-server】Code-Server 安装部署
Code-Server 安装部署 1.环境准备 可以参考 https://coder.com/docs/code-server/install code-server的安装流程进行安装,主机环境是 Centos7 建议使用 docker 方式进行安装,可能会出现如下报错,需要升级 GNC 的版本,由于影响较…...

博客摘录「 YOLOv5模型剪枝压缩」2024年5月11日
添加L1正则来约束BN层系数 语义边缘检测和语义分割的关系调研结果为,语义信息可以用来增强语义分割的效果,也有一定的优点和采用理由,但此类论文的数量并不是很多,语义分割的多数方法还是使用深度学习直接做像素分类。在对比两者…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

