轨迹优化 | 图解欧氏距离场与梯度场算法(附ROS C++/Python实现)
目录
- 0 专栏介绍
- 1 什么是距离场?
- 2 欧氏距离场计算原理
- 3 双线性插值与欧式梯度场
- 4 仿真实现
- 4.1 ROS C++实现
- 4.2 Python实现
0 专栏介绍
🔥课程设计、毕业设计、创新竞赛、学术研究必备!本专栏涉及更高阶的运动规划算法实战:曲线生成与轨迹优化、碰撞模型与检测、多智能体群控、深度强化学习运动规划、社会性导航、全覆盖路径规划等内容,每个模型都包含代码实现加深理解。
🚀详情:运动规划实战进阶
1 什么是距离场?
距离场(Distance Field)也称为距离变换(Distance Transform),在图像处理和模式识别中是一种重要工具,其核心思想是将图像中每个像素点的值表示为到最近的目标像素的距离度量,更高维的情况依次类推。在计算机视觉领域,距离场是图像分割和配准的基础,在运动规划中则常用于地图建模(广义Voronoi图计算)和轨迹梯度优化。

给定点集 G \mathcal{G} G和其上的目标点集 Q ⊆ G Q\subseteq \mathcal{G} Q⊆G,可以定义函数
D I ( p ) = min q ∈ G ( d ( p , q ) + I ( q ) ) \mathcal{D} _I\left( p \right) =\min _{q\in \mathcal{G}}\left( d\left( p,q \right) +I\left( q \right) \right) DI(p)=q∈Gmin(d(p,q)+I(q))
计算任意一点 p p p到 Q Q Q的最近距离,其中距离度量 d ( ⋅ , ⋅ ) d\left( \cdot ,\cdot \right) d(⋅,⋅)定义了距离场的属性,指示函数
I Q ( q ) = { 0 , i f q ∈ Q ∞ , o t h e r w i s e I_Q\left( q \right) =\begin{cases} 0, \mathrm{if} q\in Q\\ \infty , \mathrm{otherwise}\\\end{cases} IQ(q)={0,ifq∈Q∞,otherwise
常用的 d ( ⋅ , ⋅ ) d\left( \cdot ,\cdot \right) d(⋅,⋅)为
- 欧氏距离,此时称为欧氏距离变换(Euclidean Distance Transform, EDT)
- 曼哈顿距离,此时称为曼哈顿距离变换(Manhattan Distance Transform, MDT)
- 切比雪夫距离,此时称为切比雪夫距离变换(Chebyshev Distance Transform, CDT)
- …
2 欧氏距离场计算原理
n n n维距离场可以通过一维距离场迭代计算得到,因此只需要讨论一维EDT的计算即可。如下图左侧所示为初始计算轴的EDT计算,右侧所示为更一般的情况,此时障碍物处的采样函数叠加了前轴计算信息。

注意到 O \mathcal{O} O定义了一系列以障碍物 q ∈ O q\in \mathcal{O} q∈O为顶点的抛物线,而 ∀ p ∈ G \forall p\in \mathcal{G} ∀p∈G在系列抛物线形成的下包络的投影组成了距离场 D f ( p ) \mathcal{D} _f\left( p \right) Df(p),而下包络的计算与抛物线交点有关。联立两条抛物线 ( s − q ) 2 + f ( q ) = ( s − r ) 2 + f ( r ) \left( s-q \right) ^2+f\left( q \right) =\left( s-r \right) ^2+f\left( r \right) (s−q)2+f(q)=(s−r)2+f(r)可得
s = ( f ( r ) + r 2 ) − ( f ( q ) + q 2 ) 2 r − 2 q s=\frac{\left( f\left( r \right) +r^2 \right) -\left( f\left( q \right) +q^2 \right)}{2r-2q} s=2r−2q(f(r)+r2)−(f(q)+q2)
即任意两条抛物线有且仅有一个交点 s s s。设 K \mathcal{K} K为实际组成下包络的抛物线集合, v ( k ) v\left( k \right) v(k)表示其中第 k k k条抛物线的顶点, z ( k ) z\left( k \right) z(k)表示第 k k k条和第 k − 1 k-1 k−1条抛物线的交点,区间 [ z ( k ) , z ( k + 1 ) ) \left[ z\left( k \right) ,z\left( k+1 \right) \right) [z(k),z(k+1))表示第 k k k条抛物线的下包络范围。在遍历求解下包络过程中,对于新的抛物线 e e e,其与 K \mathcal{K} K中最新的一条抛物线 k k k的交点 s s s有两种情况:
- 若 s > z ( k ) s>z\left( k \right) s>z(k),则将 e e e添加到 K \mathcal{K} K中并更新 v ( k ) v\left( k \right) v(k)、 z ( k ) z\left( k \right) z(k);
- 若 s ⩽ z ( k ) s\leqslant z\left( k \right) s⩽z(k),则第 k k k条抛物线不参与构成下包络,应从 K \mathcal{K} K中删除并重新计算 e e e与新的第 k k k条抛物线的交点直至 s s s在 z ( k ) z(k) z(k)右侧;
算法流程如表所示

3 双线性插值与欧式梯度场
在求解梯度过程中,需要计算离散距离场的线性插值函数。以二维环境的双线性插值为例,设已知离散空间有四点坐标为 A ( x 1 , y 1 ) A\left( x_1,y_1 \right) A(x1,y1)、 B ( x 2 , y 1 ) B\left( x_2,y_1 \right) B(x2,y1) 、 C ( x 1 , y 2 ) C\left( x_1,y_2 \right) C(x1,y2)与 D ( x 2 , y 2 ) D\left( x_2,y_2 \right) D(x2,y2),对其中任意一点 P P P,首先在 x x x方向上插值
{ f ( R 1 ) = f ( x , y 1 ) = x 2 − x x 2 − x 1 f ( A ) + x − x 1 x 2 − x 1 f ( B ) f ( R 2 ) = f ( x , y 2 ) = x 2 − x x 2 − x 1 f ( C ) + x − x 1 x 2 − x 1 f ( D ) \begin{cases} f\left( R_1 \right) =f\left( x,y_1 \right) =\frac{x_2-x}{x_2-x_1}f\left( A \right) +\frac{x-x_1}{x_2-x_1}f\left( B \right)\\ f\left( R_2 \right) =f\left( x,y_2 \right) =\frac{x_2-x}{x_2-x_1}f\left( C \right) +\frac{x-x_1}{x_2-x_1}f\left( D \right)\\\end{cases} {f(R1)=f(x,y1)=x2−x1x2−xf(A)+x2−x1x−x1f(B)f(R2)=f(x,y2)=x2−x1x2−xf(C)+x2−x1x−x1f(D)
再基于插值点 R 1 R_1 R1、 R 2 R_2 R2进行 y y y方向的插值
f ( P ) = f ( x , y ) = y 2 − y y 2 − y 1 f ( R 1 ) + y − y 1 y 2 − y 1 f ( R 2 ) f\left( P \right) =f\left( x,y \right) =\frac{y_2-y}{y_2-y_1}f\left( R_1 \right) +\frac{y-y_1}{y_2-y_1}f\left( R_2 \right) f(P)=f(x,y)=y2−y1y2−yf(R1)+y2−y1y−y1f(R2)
展开可得矩阵形式
f ( x , y ) = 1 ( x 2 − x 1 ) ( y 2 − y 1 ) [ x 2 − x x − x 1 ] T [ f ( A ) f ( C ) f ( B ) f ( D ) ] [ y 2 − y y − y 1 ] f\left( x,y \right) =\frac{1}{\left( x_2-x_1 \right) \left( y_2-y_1 \right)}\left[ \begin{array}{c} x_2-x\\ x-x_1\\\end{array} \right] ^T\left[ \begin{matrix} f\left( A \right)& f\left( C \right)\\ f\left( B \right)& f\left( D \right)\\\end{matrix} \right] \left[ \begin{array}{c} y_2-y\\ y-y_1\\\end{array} \right] f(x,y)=(x2−x1)(y2−y1)1[x2−xx−x1]T[f(A)f(B)f(C)f(D)][y2−yy−y1]

对于离散栅格坐标而言, x 2 − x 1 = y 2 − y 1 = 1 x_2-x_1=y_2-y_1=1 x2−x1=y2−y1=1,设 Δ x = x − x 1 \varDelta x=x-x_1 Δx=x−x1与 Δ y = y − y 1 \varDelta y=y-y_1 Δy=y−y1,则插值函数简化为
f ( Δ x , Δ y ) = [ 1 − Δ x Δ x ] T [ f ( A ) f ( C ) f ( B ) f ( D ) ] [ 1 − Δ y Δ y ] f\left( \varDelta x,\varDelta y \right) =\left[ \begin{array}{c} 1-\varDelta x\\ \varDelta x\\\end{array} \right] ^T\left[ \begin{matrix} f\left( A \right)& f\left( C \right)\\ f\left( B \right)& f\left( D \right)\\\end{matrix} \right] \left[ \begin{array}{c} 1-\varDelta y\\ \varDelta y\\\end{array} \right] f(Δx,Δy)=[1−ΔxΔx]T[f(A)f(B)f(C)f(D)][1−ΔyΔy]
则函数 f f f在任意一点的梯度为
∇ f ( Δ x , Δ y ) = [ ∂ f ( Δ x , Δ y ) ∂ Δ x ∂ f ( Δ x , Δ y ) ∂ Δ y ] = [ [ − 1 1 ] T [ f ( A ) f ( C ) f ( B ) f ( D ) ] [ 1 − Δ y Δ y ] [ 1 − Δ x Δ x ] T [ f ( A ) f ( C ) f ( B ) f ( D ) ] [ − 1 1 ] ] \nabla f\left( \varDelta x,\varDelta y \right) =\left[ \begin{array}{c} \frac{\partial f\left( \varDelta x,\varDelta y \right)}{\partial \varDelta x}\\ \frac{\partial f\left( \varDelta x,\varDelta y \right)}{\partial \varDelta y}\\\end{array} \right] =\left[ \begin{array}{c} \left[ \begin{array}{c} -1\\ 1\\\end{array} \right] ^T\left[ \begin{matrix} f\left( A \right)& f\left( C \right)\\ f\left( B \right)& f\left( D \right)\\\end{matrix} \right] \left[ \begin{array}{c} 1-\varDelta y\\ \varDelta y\\\end{array} \right]\\ \left[ \begin{array}{c} 1-\varDelta x\\ \varDelta x\\\end{array} \right] ^T\left[ \begin{matrix} f\left( A \right)& f\left( C \right)\\ f\left( B \right)& f\left( D \right)\\\end{matrix} \right] \left[ \begin{array}{c} -1\\ 1\\\end{array} \right]\\\end{array} \right] ∇f(Δx,Δy)=[∂Δx∂f(Δx,Δy)∂Δy∂f(Δx,Δy)]=⎣⎢⎢⎡[−11]T[f(A)f(B)f(C)f(D)][1−ΔyΔy][1−ΔxΔx]T[f(A)f(B)f(C)f(D)][−11]⎦⎥⎥⎤
4 仿真实现
4.1 ROS C++实现
核心代码如下所示
GradientLayer::updateCosts(nav2_costmap_2d::Costmap2D & master_grid, int min_i, int min_j,int max_i,int max_j)
{if (!enabled_) {return;}unsigned char * master_array = master_grid.getCharMap();unsigned int size_x = master_grid.getSizeInCellsX(), size_y = master_grid.getSizeInCellsY();// Fixing window coordinates with map size if necessary.min_i = std::max(0, min_i);min_j = std::max(0, min_j);max_i = std::min(static_cast<int>(size_x), max_i);max_j = std::min(static_cast<int>(size_y), max_j);// Simply computing one-by-one cost per each cellint gradient_index;for (int j = min_j; j < max_j; j++) {// Reset gradient_index each time when reaching the end of re-calculated window// by OY axis.gradient_index = 0;for (int i = min_i; i < max_i; i++) {int index = master_grid.getIndex(i, j);// setting the gradient costunsigned char cost = (LETHAL_OBSTACLE - gradient_index*GRADIENT_FACTOR)%255;if (gradient_index <= GRADIENT_SIZE) {gradient_index++;} else {gradient_index = 0;}master_array[index] = cost;}}
}
4.2 Python实现
欧氏距离场核心代码
def compute(self, f_get, mat: np.ndarray, dim: int) -> np.array:"""Compute distance field along one-dimension baseon sample funciton f_get.Parameters:f_get (function): sample functionmat (np.ndarray): the matrix to transformdim (int): the dimension to transformReturns:df (np.array): the distance field along dim-dimension"""# initialzationk = 0n = mat.shape[dim]v, z = [0 for _ in range(n)], [0 for _ in range(n + 1)]z[0], z[1] = -self.INF, self.INF# envelopefor q in range(1, n):s = ((f_get(v[k]) + v[k] ** 2) - (f_get(q) + q ** 2)) / (2 * (v[k] - q))while s <= z[k]:k -= 1s = ((f_get(v[k]) + v[k] ** 2) - (f_get(q) + q ** 2)) / (2 * (v[k] - q))k += 1v[k] = qz[k], z[k + 1] = s, self.INF# distance calculationk = 0edf = np.zeros((n, ))for q in range(n):while z[k + 1] < q:k += 1edf[q] = (q - v[k]) ** 2 + f_get(v[k])return edf
欧氏梯度场核心代码:
def gradient(self, df: np.ndarray, x: float, y: float) -> np.array:"""To obtain the gradient at (x, y) in the distance field through bilinear interpolation.Parameters:df (np.ndarray): the distance fieldx/y (float): the query coordinateReturns:g(x, y): the gradient at (x, y)"""m, n = df.shapex, y = max(min(n - 1, x), 0), max(min(m - 1, y), 0)xi, yi = int(x), int(y)dx, dy = x - xi, y - yixi, yi = max(min(n - 1, xi), 0), max(min(m - 1, yi), 0)xp, yp = max(min(n - 1, xi + 1), 0), max(min(m - 1, yi - 1), 0)bl, br = df[yi, xi], df[yi, xp]tl, tr = df[yp, xi], df[yp, xp]return np.array([(1 - dy) * (br - bl) + dy * (tr + tl),-((1 - dx) * (tl - bl) + dx * (tr - br))])
效果如下所示

一个实际地图的案例如下

完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

轨迹优化 | 图解欧氏距离场与梯度场算法(附ROS C++/Python实现)
目录 0 专栏介绍1 什么是距离场?2 欧氏距离场计算原理3 双线性插值与欧式梯度场4 仿真实现4.1 ROS C实现4.2 Python实现 0 专栏介绍 🔥课程设计、毕业设计、创新竞赛、学术研究必备!本专栏涉及更高阶的运动规划算法实战:曲线生成…...

【二维差分】2132. 用邮票贴满网格图
本文涉及知识点 二维差分 LeetCode2132. 用邮票贴满网格图 给你一个 m x n 的二进制矩阵 grid ,每个格子要么为 0 (空)要么为 1 (被占据)。 给你邮票的尺寸为 stampHeight x stampWidth 。我们想将邮票贴进二进制矩…...
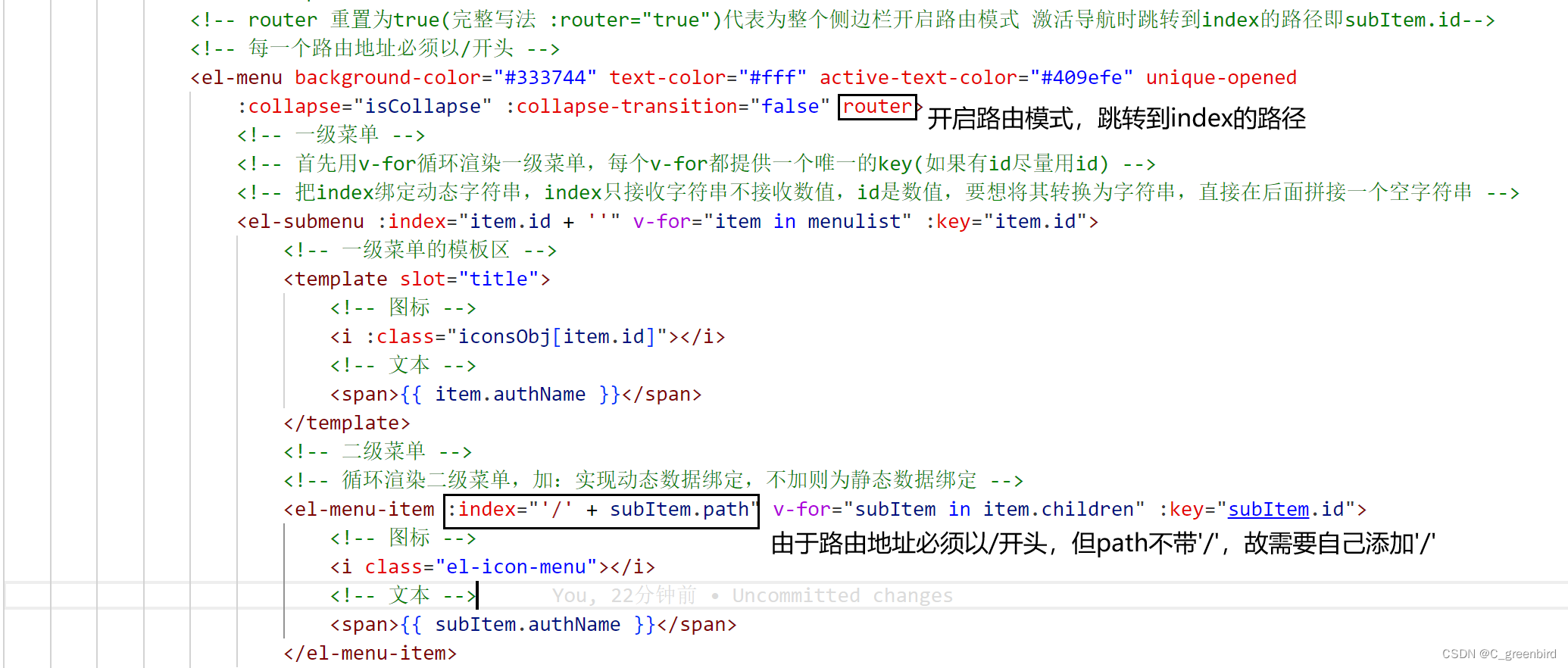
【前端项目笔记】2 主页布局
主页布局 element-ui提供的组件名称就是它的类名 ☆☆ CSS选择器: (1)基本选择器 类型选择器 p/span/div…… 类选择器 (.classname) ID选择器 (#idname) 通配选择器 ( * ) (2)属性选择器 选择具有特定属性或属性值的…...

t265 jetpack 6 px4 ros2
Ubuntu22.04 realsenseSDK2和ROS2Wrapper安装方法,包含T265版本踩坑问题_ros2 realsense-CSDN博客 210 git clone https://github.com/IntelRealSense/librealsense.git 212 git branch 215 git tag 218 git checkout v2.51.1 219 git branch 265 git clone https://…...
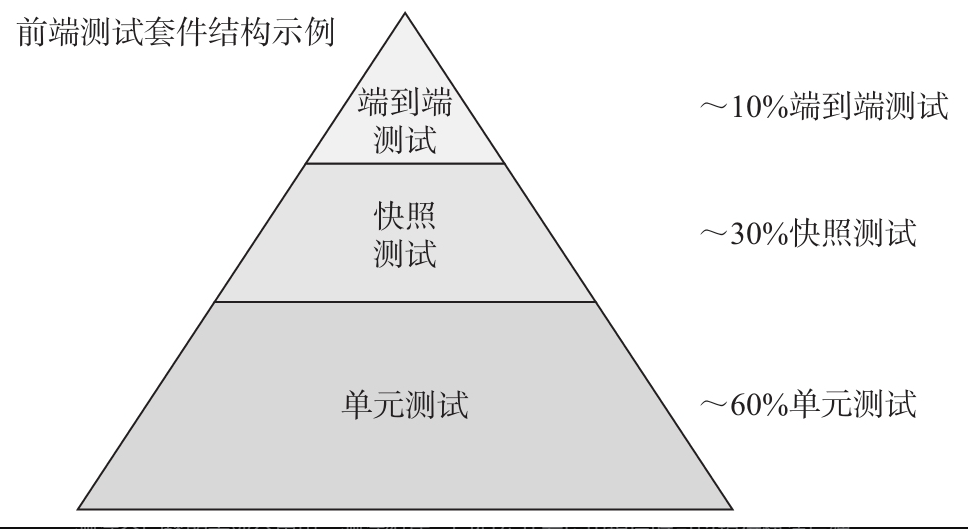
vue 应用测试(一) --- 介绍
vue 应用测试(一) ---介绍 前端测试简介组件测试Jest 测试框架简介其他测试框架 第一个测试避免误报如何组织测试代码 组件挂载Vue2 组件挂载的方式Vue3 的挂载方式vue-test-utils挂载选项 如何调试测试用例参考小结 前端测试简介 软件测试:…...

Perl 语言入门学习
一、介绍 Perl 是一种高级的、动态的、解释型的通用编程语言,由Larry Wall于1987年开发。它是一种非常灵活和强大的语言,广泛用于文本处理、系统管理、网络编程、图形编程等领域。 Perl 语言的设计理念是“用一种简单的语法,去解决复杂的编…...

HarmongOS打包[保姆级]
创建应用 首先进入 华为开发者联盟-HarmonyOS开发者官网 然后进行登录。 登录成功后,鼠标悬停在在登录右上角那个位置后再点击管理中心,进入下面这个界面。 再点击:应用服务–>应用发布–>新建–>完善信息 构建和生成私钥和证书请求…...

SpringBoot怎么实现自定义接口全局异常捕获?详细教程
自定义异常 package com.single.bean;import org.springframework.core.NestedRuntimeException;public class FDWException extends NestedRuntimeException {private static final long serialVersionUID = 6046035491210083235L;public FDWException(String msg) {super(msg…...

Ms08067安全实验室成功实施多家业务系统渗透测试项目
点击星标,即时接收最新推文 近日,Ms08067安全实验室针对多家公司重要系统实施渗透测试项目。公司网络信息系统的业务应用和存储的重要信息资产均较多,存在网络系统结构的复杂性和庞杂等特点,使得公司网络信息系统面临一定风险。项…...

小熊家政帮day22-day23 订单系统优化(订单状态机、练习分库分表、索引、订单缓存)
目录 1 状态机1.1 状态机介绍1.1.1 当前存在的问题1.1.2 使用状态机解决问题 1.2 实现订单状态机1.2.1 编写订单状态机1.2.1.1 依赖引入1.2.1.2 订单状态枚举类1.2.1.3 状态变更事件枚举类1.2.1.4 定义订单快照类1.2.1.5 定义事件变更动作类1.2.1.5 定义订单状态机类1.2.1.6 状…...

LeetCode 1731, 151, 148
目录 1731. 每位经理的下属员工数量题目链接表要求知识点思路代码 151. 反转字符串中的单词题目链接标签思路代码 148. 排序链表题目链接标签Collections.sort()思路代码 归并排序思路代码 1731. 每位经理的下属员工数量 题目链接 1731. 每位经理的下属员工数量 表 表Emplo…...

Codeforces Round 953 (Div. 2)(A~D题解)
这次比赛是我最顺利的一次比赛,也是成功在中途打进前1500,写完第三道题的时候也是保持在1600左右,但是后面就啥都不会了,还吃了点罚时,虽说如此也算是看到进步了,D题学长说很简单,但是我当时分析…...

晶圆切割机(晶圆划片机)为晶圆加工重要设备 我国市场国产化进程不断加快
晶圆切割机(晶圆划片机)为晶圆加工重要设备 我国市场国产化进程不断加快 晶圆切割机又称晶圆划片机,指能将晶圆切割成芯片的机器设备。晶圆切割机需具备切割精度高、切割速度快、操作便捷、稳定性好等特点,在半导体制造领域应用广…...
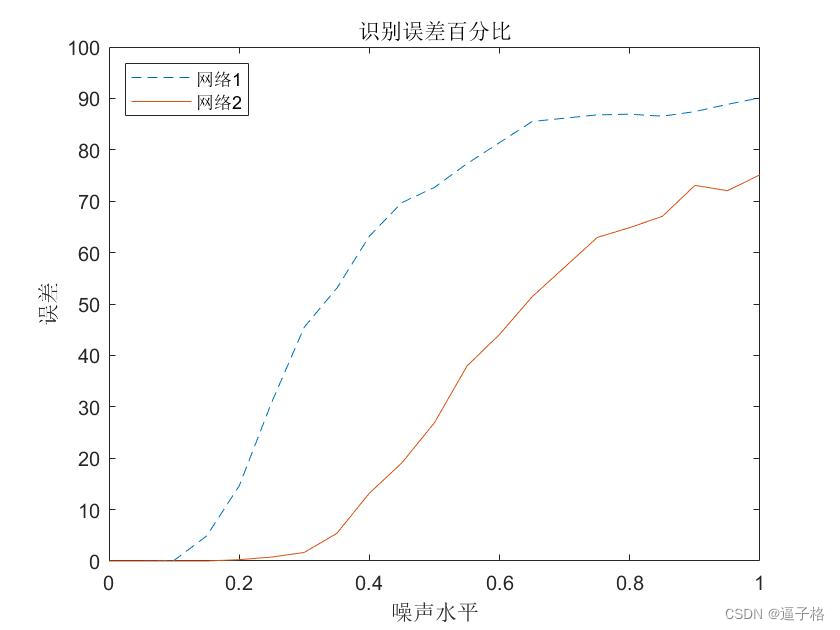
39、基于深度学习的(拼音)字符识别(matlab)
1、原理及流程 深度学习中常用的字符识别方法包括卷积神经网络(CNN)和循环神经网络(RNN)。 数据准备:首先需要准备包含字符的数据集,通常是手写字符、印刷字符或者印刷字体数据集。 数据预处理࿱…...

CCF 矩阵重塑
第一题:矩阵重塑(一) 本题有两种思路 第一种 (不确定是否正确 但是100分) #include<iostream> using namespace std; int main(){int n,m,p,q,i,j;cin>>n>>m>>p>>q;int a[n][m];for(i…...

Aigtek高压放大器在柔性爬行机器人驱动性能研究中的应用
实验名称:柔性爬行机器人的材料测试 研究方向:介电弹性体的最小能量结构是一种利用DE材料的电致变形与柔性框架形变相结合设计的新型柔性驱动器,所谓最小能量是指驱动器在平衡状态时整个系统的能量最小,当系统在外界的电压刺激下就…...

Postman下发流表至Opendaylight
目录 任务目的 任务内容 实验原理 实验环境 实验过程 1、打开ODL控制器 2、网页端打开ODL控制页面 3、创建拓扑 4、Postman中查看交换机的信息 5、L2层流表下发 6、L3层流表下发 7、L4层流表下发 任务目的 1、掌握OpenFlow流表相关知识,理解SDN网络中L…...

C语言王国——数组的旋转(轮转数组)三种解法
目录 一、题目 二、分析 2.1 暴力求解法 2.2 找规律 2.3 追求时间效率,以空间换时间 三、结论 一、题目 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出…...

MySQL中CAST和CONVERT函数都用于数据类型转换
在 MySQL 中,CAST() 和 CONVERT() 函数都用于数据类型转换。虽然这两个函数在大多数情况下可以互换使用,但它们之间还是有一些细微的差别。 官方文档地址 https://dev.mysql.com/doc/refman/8.4/en/cast-functions.html#function_cast CAST() 函数 C…...

速盾:cdn影响seo吗?
CDN (Content Delivery Network) 是一个分布式网络架构,用于在全球范围内加速网站内容的传输和分发。它通过将网站的静态资源(例如图片、CSS、JavaScript 文件等)存储在多个服务器上,使用户可以从最接近他们位置的服务器上获取这些…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...
