论文阅读(一种新的稀疏PCA求解方式)Sparse PCA: A Geometric Approach
这是一篇来自JMLR的论文,论文主要关注稀疏主成分分析(Sparse PCA)的问题,提出了一种新颖的几何解法(GeoSPCA)。
该方法相比传统稀疏PCA的解法的优点:1)更容易找到全局最优;2)计算效率更高;3)因为不再需要计算存储整个协方差矩阵,所以对存储资源需求更少;4)GeoSPCA能够一次性构建所有主成分,而不是通过迭代的方式逐步添加,这有助于避免因迭代过程中的数据秩减而导致的信息损失。
这个笔记不会记录原文中过于数学的证明和推理部分,仅整理原理、结论和算法流程等。对数学推理感兴趣的,可自行到以下地址查看原文:
https://www.jmlr.org/papers/volume24/22-0088/22-0088.pdf
1,什么是稀疏PCA
首先给不了解的读者补充一下稀疏PCA概念:
普通PCA得到的主成分有大量非0的原始变量,所以主成分其实是不太清晰的。稀疏PCA通过减少构建主成分的变量数量,可以提高模型的可解释性、预测能力或降低操作成本。相比较而言,稀疏PCA更适用于需要模型解释性的场景。
稀疏PCA 在普通PCA的基础上,引入了一个惩罚函数。这样做的目的是使得大部分系数变为零,从而凸现出主成分的主要部分。
稀疏PCA的实现通常涉及到在标准的PCA优化问题中加入一个正则化项,以促使某些系数变为零。
2,现有稀疏PCA计算方式的缺陷
大多数现有方法通过迭代方式构建主成分(PCs),这些方法通常无法保证整体最优解,且计算成本较高。
3,本文提出的GeoSPCA方法
这种方法通过将问题转化为一个二元线性优化问题(BLO)来近似原始问题,从而绕开了非凸优化的问题。
GeoSPCA算法一次性构建所有主成分,而不是通过迭代的方式。这种方法通过引入一个参数η来近似原始问题,并通过一系列切割平面算法(cut generation algorithm)来逐步改进解。
切割平面算法的核心思想是逐步添加约束条件(即切割平面),以逼近问题的最优解。
3.1 整体流程思路:
-
初始化:算法开始时,首先解决一个没有额外约束的基本二元线性优化问题(BLO),以获得初始解。
-
计算当前解的正交投影:对于当前解,计算数据矩阵在由当前解定义的子空间上的正交投影。
-
检查投影误差:计算当前解的正交投影与原始数据矩阵之间的差异(即误差)。如果这个误差小于预设的阈值η,当前解就是可接受的。
-
生成切割平面:如果投影误差超过阈值η,算法会生成一个新的线性约束(切割平面),该约束会排除当前解,迫使算法在下一次迭代中寻找更好的解。
-
迭代过程:将新生成的切割平面添加到优化问题中,并重新解决BLO问题以获得新的解。这个过程会不断重复,直到找到满足误差阈值的解或达到预设的迭代次数。
-
终止条件:算法在以下情况下终止:1)找到一个满足误差阈值η的解。2)达到预设的最大迭代次数。3)无法进一步改进当前解。
注:其中,线性约束(也称为切割平面或切割约束)是一种限制变量取值范围的表达式,它以线性方程或不等式的形式出现。
3.2 具体落实的算法
在具体落实层面,原文提出了2个算法。
算法1在给定参数η的情况下,找到一组最优支持(Optimal support),这些支持用于构建稀疏主成分。
算法2是从较大的η值开始,逐步细化η的值,以逼近最优的η值,同时也获得稀疏PCA的最优解。
算法1:
算法步骤如下:
-
初始化:开始时,使用一个二元线性优化(BLO)问题,目标是最大化数据矩阵列的范数加权和,约束条件是支持的大小不超过k。
-
求解BLO问题:使用BLO求解器找到当前问题的最优解 s∗。
-
计算正交投影:对找到的解 s∗,计算数据矩阵在由解 s∗ 定义的子空间上的正交投影,并求解PCA以得到对应的主成分。
-
检查投影误差:计算正交投影与原始数据矩阵之间的Frobenius范数误差 η(s∗)。(注:两个矩阵之间的Frobenius范数一般指的是两个矩阵差的Frobenius范数,也就是同位置元素相减后的平方和的平方根)
-
生成切割平面:如果误差 η(s∗)超过给定的阈值η,则生成一个新的线性约束(切割平面),将其添加到BLO问题中,以排除当前解。
-
迭代:重复求解BLO问题,并根据需要生成和添加新的切割平面,直到找到满足误差阈值的解。
-
返回结果:算法返回找到的支持集,这些支持集定义了稀疏主成分。
算法2:
算法步骤如下:
-
初始化:设置初始η值 η0和最优解的η值 η∗ 为较大的值。
-
迭代过程:进行多次迭代,每次迭代使用算法1来求解当前η值下的BLO问题。
-
更新η值:如果当前解的η值 ηt小于 η∗,并且当前解的函数值 f(ηt) 高于 η∗,则更新 η∗为 ηt,并减小η值以进行下一步迭代。
-
检查停止条件:如果经过λ次迭代后没有改进,或者达到预设的迭代次数,则停止迭代。
-
返回结果:算法返回找到的近似最优解的支持集 s∗,以及对应的η值 η∗和函数值 f(η*)。
相关文章:
Sparse PCA: A Geometric Approach)
论文阅读(一种新的稀疏PCA求解方式)Sparse PCA: A Geometric Approach
这是一篇来自JMLR的论文,论文主要关注稀疏主成分分析(Sparse PCA)的问题,提出了一种新颖的几何解法(GeoSPCA)。 该方法相比传统稀疏PCA的解法的优点:1)更容易找到全局最优ÿ…...
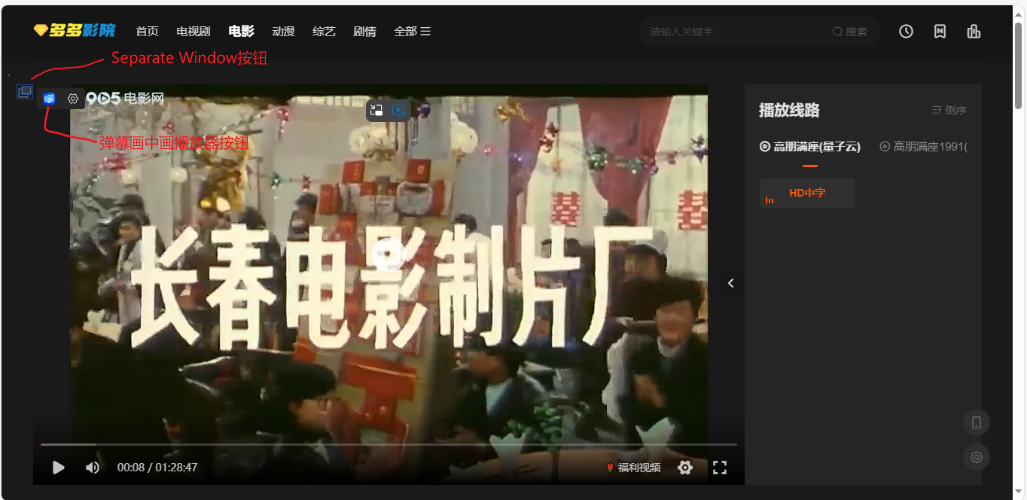
Chrome/Edge浏览器视频画中画可拉动进度条插件
目录 前言 一、Separate Window 忽略插件安装,直接使用 注意事项 插件缺点 1 .无置顶功能 2.保留原网页,但会刷新原网页 3.窗口不够美观 二、弹幕画中画播放器 三、失败的尝试 三、Potplayer播放器 总结 前言 平时看一些视频的时候ÿ…...

pg修炼之道学习笔记
一、数据库逻辑结构介绍 1、一个pg数据库服务下有多个db(多个数据库),当应用连接到一个数据库时,一般只能访问这个数据库中的数据,而不能访问其他数据库的内容(限制) 2、表索引:一…...

使用宝塔面板部署Django应用(不成功Kill Me!)
使用宝塔面板部署Django应用 文章目录 使用宝塔面板部署Django应用 本地操作宝塔面板部署可能部署失败的情况 本地操作 备份数据库 # 备份数据库 mysqldump -u root -p blog > blog.sql创建requirements # 创建requirements.txt pip freeze > requirements.txt将本项目…...

c++深拷贝、浅拷贝
在 C 中,深拷贝和浅拷贝是两个重要的概念,尤其在涉及动态内存分配和指针成员时。这两个概念描述了对象复制时的行为。 浅拷贝 浅拷贝是指复制对象时,仅复制对象的基本数据成员,对于指针成员,只复制指针地址ÿ…...

k8s核心组件
Master组件: kube-apiserver:用于暴露Kubernetes API,任何资源请求或调用操作都是通过kube-apiserver提供的接口进行。它是Kubernetes集群架构的大脑,负责接收所有请求,并根据用户的具体请求通知其他组件工作。etcd&am…...

反编译腾讯vmp
反编译腾讯vmp 继续学习的过程 多翻译几个vmp 学习 看看他们的是怎么编译的 写一个自己的vmp function __TENCENT_CHAOS_VM(U, T, g, D, j, E, K, w) {// U指令起点// T是指令list// g是函数this 或window对象// D是内部变量和栈}for (0; ;)try {for (var B !1; !B;) {let no…...

Ollama:本地部署大模型 + LobeChat:聊天界面 = 自己的ChatGPT
本地部署大模型 在本地部署大模型有多种方式,其中Ollama方式是最简单的,但是其也有一定的局限性,比如大模型没有其支持的GGUF二进制格式,就无法使用Ollama方式部署。 GGUF旨在实现快速加载和保存大语言模型,并易于阅读…...

JS中splice怎么使用
在JavaScript中,splice() 是一个数组方法,用于添加/删除项目,并返回被删除的项目。这个方法会改变原始数组。 splice() 方法的基本语法如下: array.splice(start[, deleteCount[, item1[, item2[, ...]]]]) start(必…...
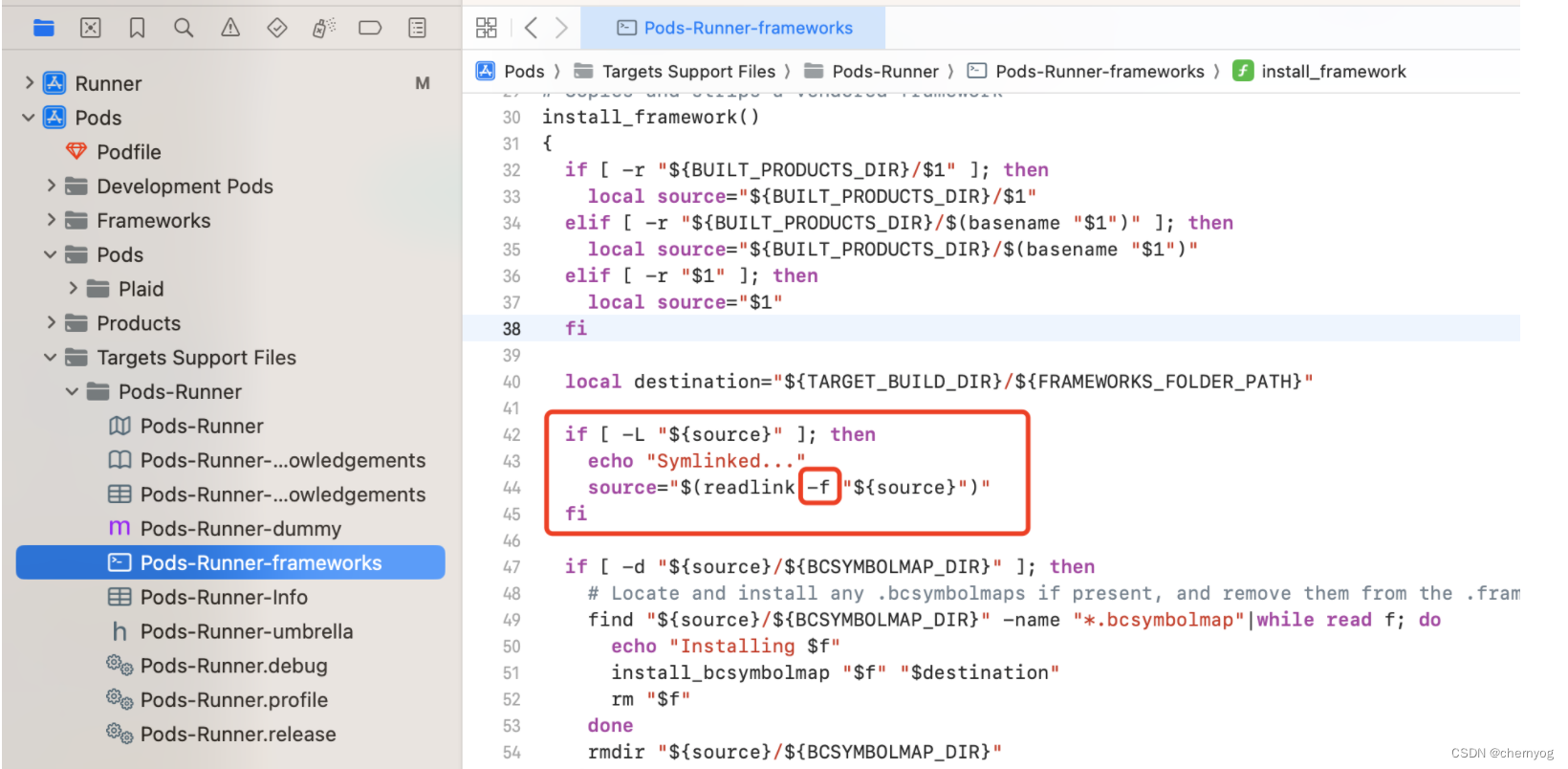
Flutter项目,Xcode15, 编译正常,但archive报错
错误提示 PhaseScriptExecution [CP]\ Embed\ Pods\ Frameworks /Users/目录/Developer/Xcode/DerivedData/Runner-brgnkruocugbipaswyuwsjsnqkzm/Build/Intermediates.noindex/ArchiveIntermediates/Runner/IntermediateBuildFilesPath/Runner.build/Release-iphoneos/Runner…...

云动态摘要 2024-06-17
给您带来云厂商的最新动态,最新产品资讯和最新优惠更新。 最新优惠与活动 [低至1折]腾讯混元大模型产品特惠 腾讯云 2024-06-06 腾讯混元大模型产品特惠,新用户1折起! 云服务器ECS试用产品续用 阿里云 2024-04-14 云服务器ECS试用产品续用…...

【JavaScript脚本宇宙】图像处理新纪元:探索六大JavaScript图像处理库
揭开图像处理的奥秘:六款顶级JavaScript库详解 前言 在现代Web开发中,图像处理变得越来越重要。从图像比较到图像编辑,每个步骤都需要高效、强大的工具来完成。JavaScript生态系统为开发者提供了丰富的图像处理库,这些库不仅功能…...

使用python调ffmpeg命令将wav文件转为320kbps的mp3
320kbps竟然是mp3的最高采样率,有点低了吧。 import os import subprocessif __name__ __main__:work_dir "D:\\BaiduNetdiskDownload\\周杰伦黑胶\\魔杰座" fileNames os.listdir(work_dir)for filename in fileNames:pure_name, _ os.path.spli…...

程序启动 报错 no main manifest attribute
1、报错问题 未找到启动类 2、可能的原因 启动没加注解maven打包插件没有设置...

java-内部类 2
### 8. 内部类的访问规则和限制 #### 8.1 访问外部类的成员 内部类可以直接访问外部类的成员变量和方法,包括私有成员。例如: java class OuterClass { private String outerField "Outer field"; class InnerClass { void di…...
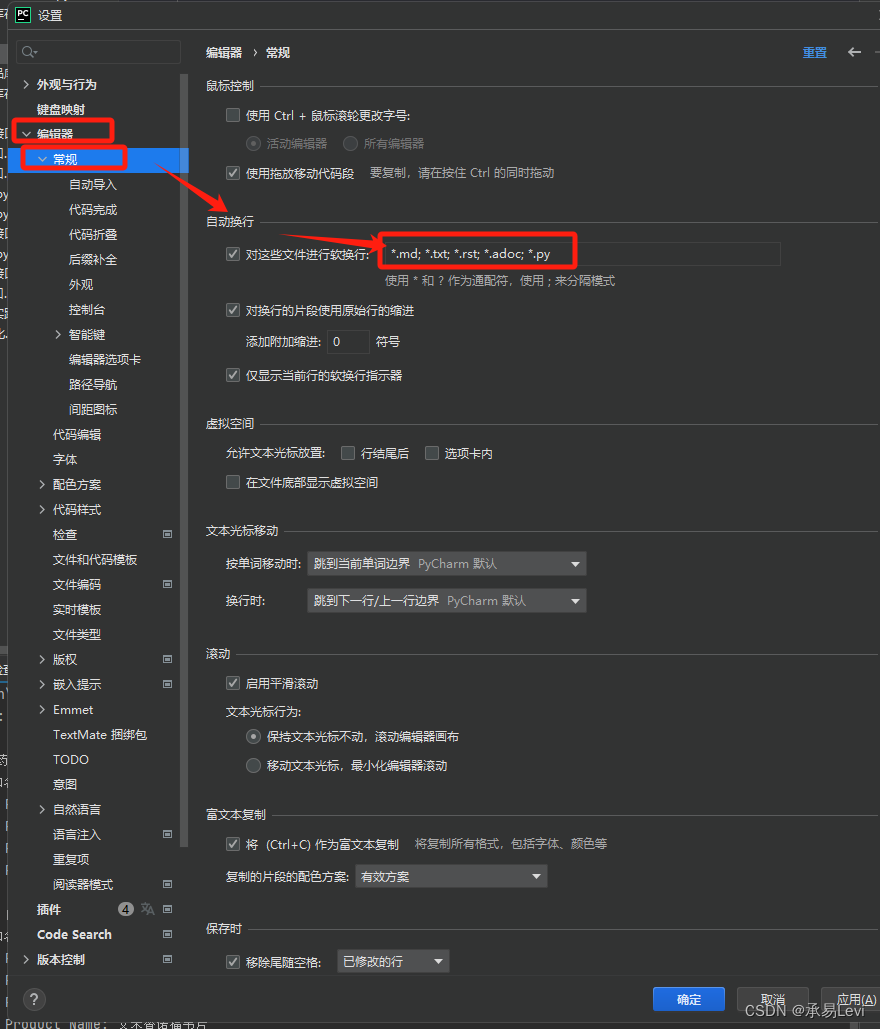
【小技巧】pycharm中自动换行的实现
pycharm如何自动换行 pycharm在setting里面设置自动化换行 具体步骤如下: (我这边用的版本为PyCharm 2023.3版本) 1、打开pycharm,选择“file”(文件) 2、选择“Setting“(设置)…...
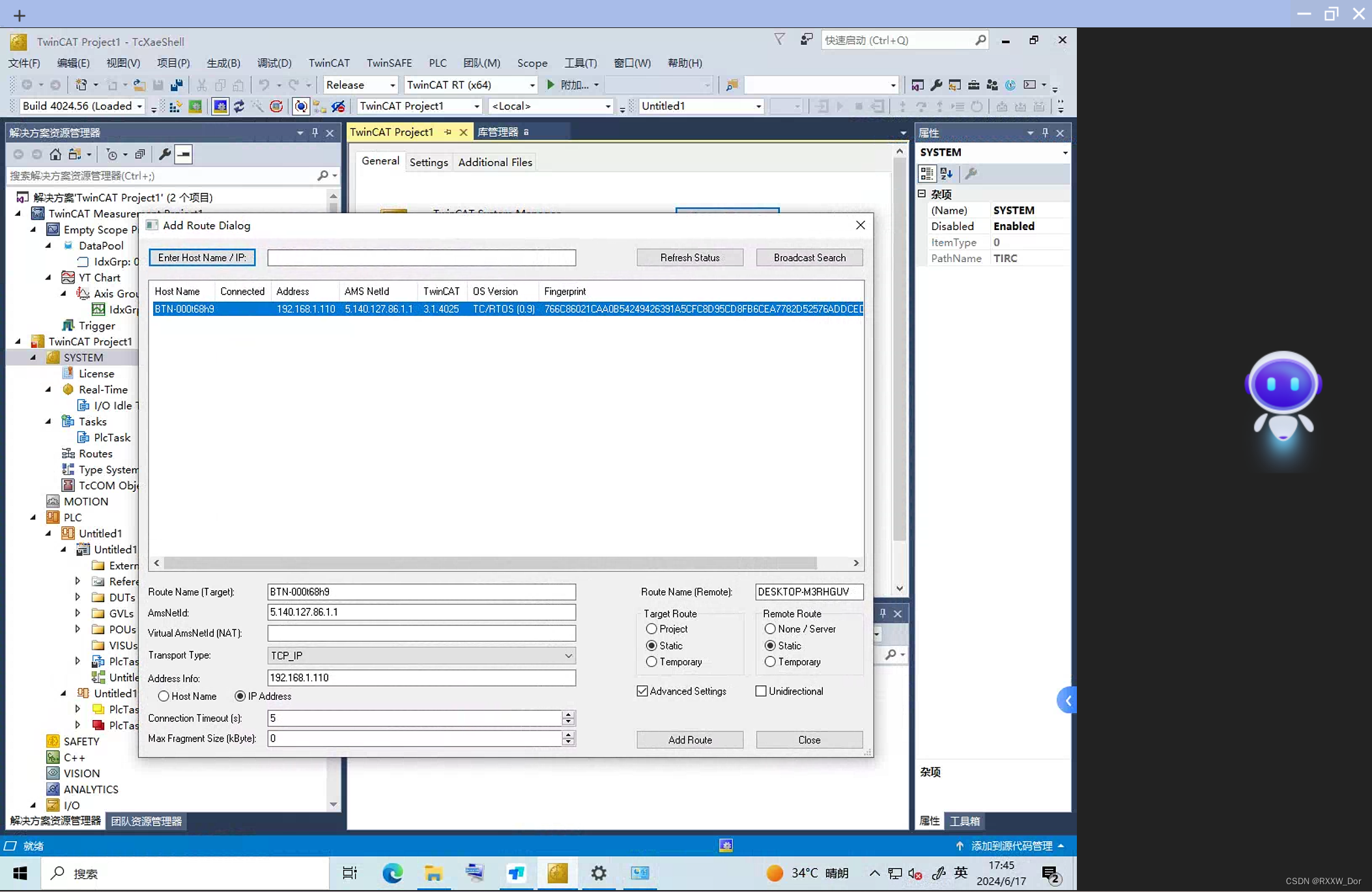
如何修改倍福CX7000PLC IP地址
我们可以通过登录网页修改PLC的IP地址,这个需要我们知道PLC的初始IP地址 1、浏览器直接输入PLC 的IP地址 2、点击修改按钮(就是那个旋转) 修改IP地址前DHCP要先disable关闭 。 3、DHCP关闭 4、点击保存 5、在CAT3里搜索 在SYSTEM双击,之后点击搜索,具体过程可以参考下…...

python安装flask,flask框架,使用静态文件、模板、get和post请求
flask框架安装 pip install flask1.创建app.py文件 启动运行 # 导入Flask类 from flask import Flask#Flask类接收一个参数__name__ app Flask(__name__)# 装饰器的作用是将路由映射到视图函数index app.route(/) def index():return Hello World# Flask应用程序实例的run方…...
Docker:Harbor
目录 一、Harbor介绍 二、安装 Harbor 2.1 环境准备 2.2下载 Harbor 3.3 修改配置(可选) 3.4 启动 Harbor 3.5访问 Harbor 三、使用 Harbor 3.1 管理Harbor 一、Harbor介绍 Docker Harbor 是由 VMware 公司开源的一款企业级的 Docker Registry …...

2024 6.10~6.16 周报
一、上周工作 完成毕设 二、本周计划 吴恩达的机器学习、实验-回顾之前密集连接部分,调整损失函数 三、完成情况 3.1 机器学习的两种主要类型: 监督学习(supervised learning)(实际中使用最多的)&…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
