matlab线性多部法求常微分方程数值解
用Adamas内差二步方法,内差三步方法,外差二步方法,外差三步方法这四种方法计算。


中k为1和2.

k为2和3
代码
function chap1_adams_methodu0 = 1;
T = 2;
h = 0.1;
N= T/h;
t = 0:h:T;
solu = exact1(t);f = @f1;
u_inter_2s = adams_inter_2steps(f,u0,t,h,N);
u_extra_2s = adams_extra_2steps(f,u0,t,h,N);
figure(1)
plot(t,u_inter_2s,'*',t,u_extra_2s, 'o',t, solu,'r')
legend('Adams-inter-2s', 'Adams-extra-2s','Exact-soln')u_inter_3s = adams_inter_3steps(f,u0,t,h,N);
u_extra_3s = adams_extra_3steps(f,u0,t,h,N);
figure(2)
plot(t, u_inter_3s,'*', t, u_extra_3s, 'o', t, solu, 'r')
legend('Adams-inter-3s', 'Adams-extra-3s', 'Exact-soln')endfunction u = adams_inter_2steps(f, u0,t,h,N)
u = zeros(N+1,1);
u(1) = u0;
% u(2) = u(1) + h*f(t(1), u(1)) ;
u(2) = exact1(1*h);
eps_in = 1e-6;
K_in = 6;
for n = 2:Nf_nm1 = f(t(n-1),u(n-1));f_n = f(t(n), u(n));s1 = u(n);du = 1;k = 1;
while abs(du)>eps_in & k<K_ins2 = u(n) + h*( 5*f(t(n+1), s1)+ 8*f_n - f_nm1 )/12;du = s2- s1;s1 = s2;k = k + 1;
end
u(n+1) = s2;
end
endfunction u = adams_inter_3steps(f, u0,t,h,N)
u = zeros(N+1,1);
u(1) = u0;
% u(2) = u(1) + h*f(t(1), u(1)) ;
% u(3) = u(2) + h*f(t(2), u(2)) ;
u(2) = exact1(1*h);
u(3) = exact1(2*h);
eps_in = 1e-6;
K_in = 6;
for n = 3:Nf_nm2 = f(t(n-2), u(n-2));f_nm1 = f(t(n-1), u(n-1));f_n = f(t(n), u(n)); s1 = u(n);du = 1;k = 1;
while abs(du)>eps_in & k<K_ins2 = u(n)+ h*(9*f(t(n+1),s1) + 19*f_n - 5*f_nm1 + f_nm2 ) /24;du = s2 - s1;s1 = s2;
k = k + 1;end
u(n+1) = s2;
end
endfunction u = adams_extra_2steps(f,u0,t,h,N)
u = zeros(N+1,1);
u(1) = u0;
% u(2) = u(1) + h*f(t(1), u(1)) ;
u(2) = exact1(h);
for n = 2:N
f_nm1 = f(t(n-1), u(n-1));
f_n = f(t(n), u(n));
u(n+1) = u(n)+ h*( 3*f_n - f_nm1 )/2;
end
endfunction u = adams_extra_3steps(f, u0,t, h,N)
u = zeros(N+1,1);
u(1) = u0;
% u(2) = u(1) + h*f(t(1), u(1)) ;
% u(3) = u(2) + h*f(t(2), u(2));
u(2) = exact1(1*h);
u(3) = exact1(2*h);
eps_in = 1e-6;
for n = 3:N
f_nm2 = f(t(n-2), u(n-2));
f_nm1 = f(t(n-1), u(n-1));
f_n = f(t(n), u(n));
u(n+1) = u(n)+ h*( 23*f_n - 16*f_nm1 + 5*f_nm2 )/12;
end
endfunction f = f1(t, u)
f = -5*u ;
endfunction f = exact1(t)
f = exp(-5*t);
end
结果:

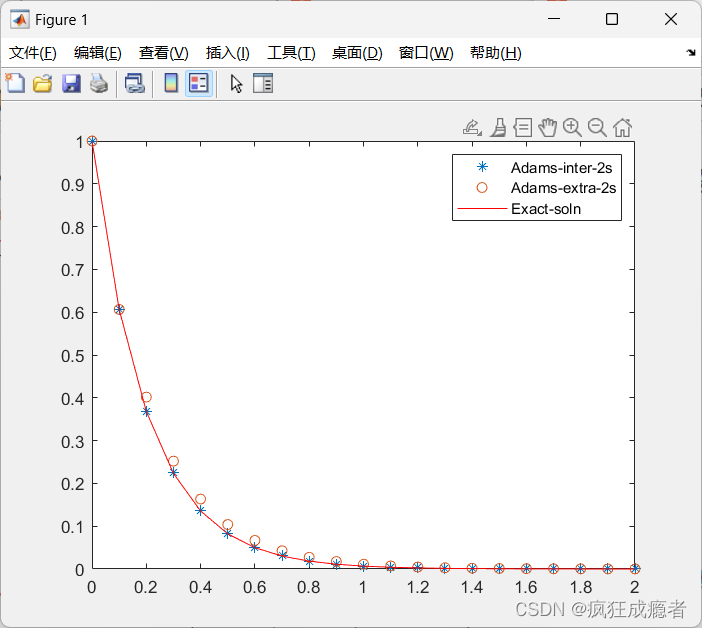
相关文章:

matlab线性多部法求常微分方程数值解
用Adamas内差二步方法,内差三步方法,外差二步方法,外差三步方法这四种方法计算。 中k为1和2. k为2和3 代码 function chap1_adams_methodu0 1; T 2; h 0.1; N T/h; t 0:h:T; solu exact1(t);f f1; u_inter_2s adams_inter_2steps(…...

前端页面实现【矩阵表格与列表】
实现页面: 1.动态表绘制(可用于矩阵构建) <template><div><h4><b>基于层次分析法的权重计算</b></h4><table table-layout"fixed"><thead><tr><th v-for"(_, colI…...

GPT4v和Gemini-Pro调用对比
要调用 GPT-4 Vision (GPT-4V) 和 Gemini-Pro,以下是详细的步骤分析,包括调用流程、API 使用方法和两者之间的区别,以及效果对比和示例。 GPT-4 Vision (GPT-4V) 调用步骤 GPT-4 Vision 主要通过 OpenAI 的 API 进行调用,用于处…...
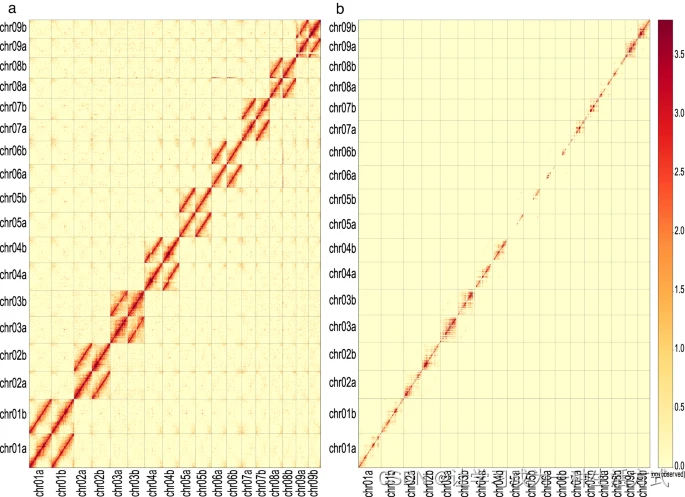
破布叶(Microcos paniculata)单倍型染色体级别基因组-文献精读22
Haplotype-resolved chromosomal-level genome assembly of Buzhaye (Microcos paniculata) 破布叶、布渣叶(Microcos paniculata)单倍型解析染色体级别基因组组装 摘要 布渣叶(Microcos paniculata)是一种传统上用作民间药物和…...
浅谈RC4
一、什么叫RC4?优点和缺点 RC4是对称密码(加密解密使用同一个密钥)算法中的流密码(一个字节一个字节的进行加密)加密算法。 优点:简单、灵活、作用范围广,速度快 缺点:安全性能较差&…...

uniapp微信小程序开发物料
开发工具 HBuilder: HBuilderX-高效极客技巧 vscode 1、在vscode中新建一个项目npx degit dcloudio/uni-preset-vue#vite-ts 项目名称 2、在HBuilder中可以可视化进行新建项目 路由 在app.json文件中配置pages路由路径 路由跳转方法 uni.navigateTo(OBJECT)…...
大数据工程师如何做到数据可视化?
好的数据可视化作品都是通过不断的数据对比分析实战出来的。 今天给大家带来一篇大数据工程师干货,从多角度解析做数据可视化的重要性,并解读一些适用的应用场景。大数据工程师们刷到这篇文章时一定要进来看看,满满的干货。 目录 1. 什么是数…...

Java 序列化与反序列化
Java 序列化是一种将对象的状态转换为字节流的机制,以便可以将该对象的状态保存到文件、数据库或通过网络传输。在反序列化过程中,这些字节流可以被重新转换为对象。序列化主要用于以下几种情况: 持久化存储:将对象的状态保存到文…...

自定义防抖注解
问题场景 在开发中由于可能存在的网络波动问题导致用户重复提交,所以自定义一个防抖注解。设计思路:自定义注解加在接口的方法上,注解中设置了SPEL表达式,可以通过SPEL表达式从接口参数中提取Redis的Key,以这个Key作为…...
【尚庭公寓SpringBoot + Vue 项目实战】登录管理(十八)
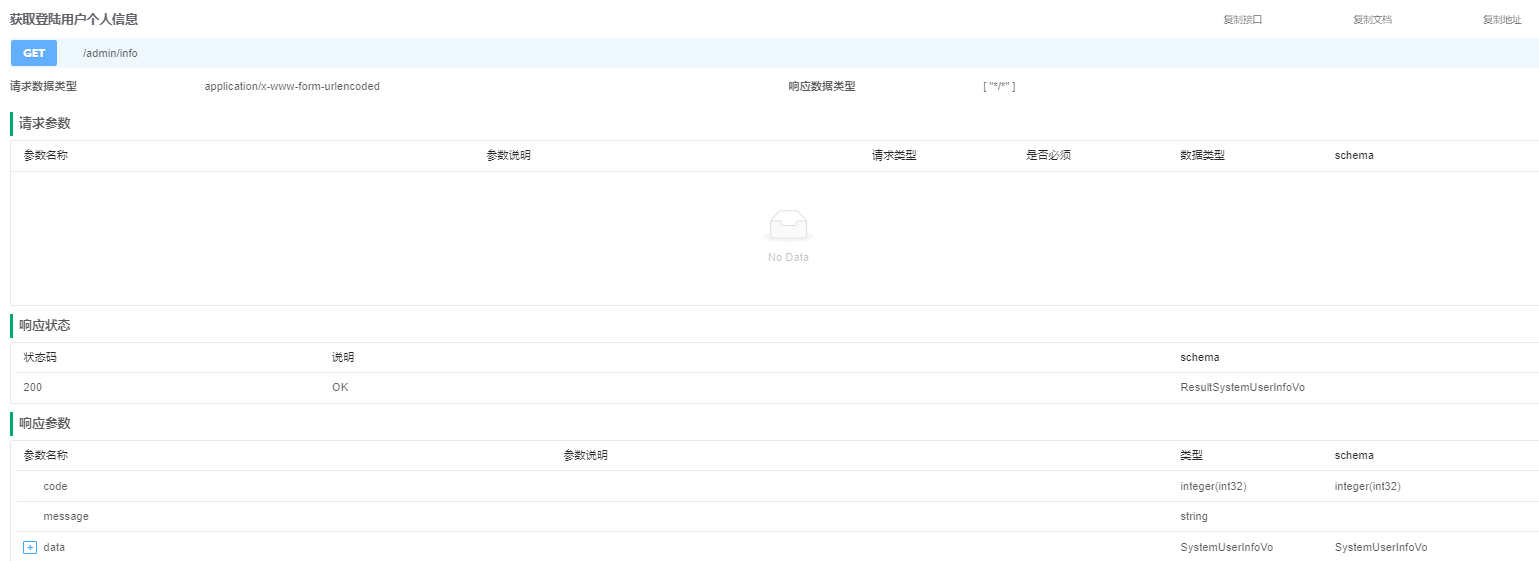
【尚庭公寓SpringBoot Vue 项目实战】登录管理(十八) 文章目录 【尚庭公寓SpringBoot Vue 项目实战】登录管理(十八)1、登录业务介绍2、接口开发2.1、获取图形验证码2.2、登录接口2.3、获取登录用户个人信息 1、登录业务介绍 登…...

【html】用html+css做地表最强王者荣耀辅助工具
源码: <!DOCTYPE html> <html><head><meta charset"utf-8" /><title></title><style>* {margin: 0;padding: 0;}body{background-color: blue;}.con {width: 300px;height: 500px;background-color: rgba(230,…...
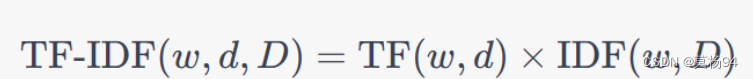
TF-IDF、BM25传统算法总结
1. TF-IDF算法 F-IDF(词频-逆文档频率)是一种用于衡量文本中词语重要性的方法,特别适用于信息检索和文本挖掘任务。下面会拆分为两部分深入讲解TF-IDF的计算过程,以便更好地理解。 TF-IDF的计算过程可以分为两个主要部分…...
项目五 OpenStack镜像管理与制作
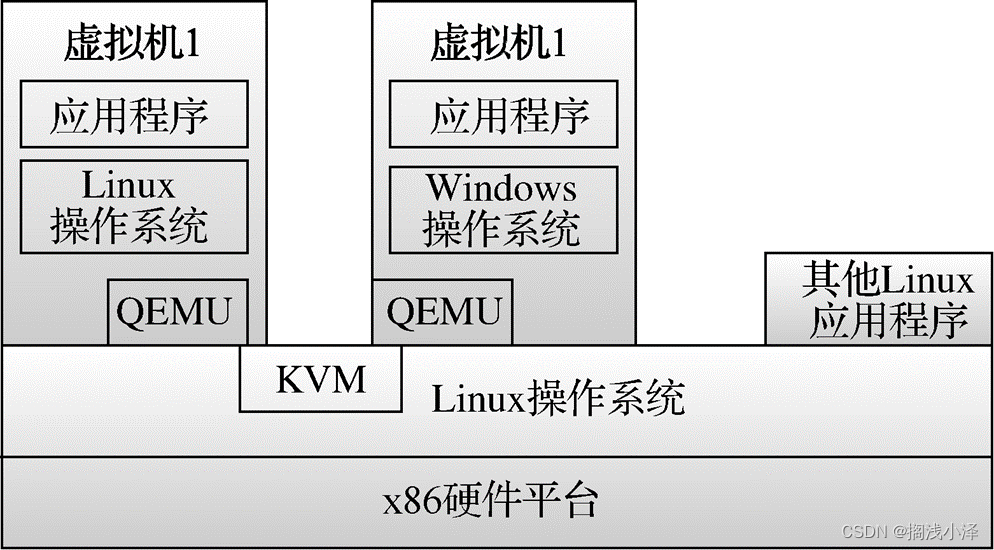
任务一 理解OpenStack镜像服务 1.1 •什么是镜像 • 镜像通常 是指一系列文件或一个磁盘驱动器的精确副本 。 • 虚拟机 所使用的虚拟磁盘, 实际上是 一种特殊格式的镜像文件 。 • 云 环境下尤其需要 镜像。 • 镜像 就是一个模板,类似于 VMware 的虚拟…...

LabVIEW回热系统热经济性分析及故障诊断
开发了一种利用LabVIEW软件的电厂回热系统热经济性分析和故障诊断系统。该系统针对火电厂回热加热器进行优化,通过实时数据监控与分析,有效提高机组的经济性和安全性,同时降低能耗和维护成本。系统的实施大幅提升了火电厂运行的效率和可靠性&…...

设计模式-迭代器模式
目录 一:基本介绍 二:原理说明 三:案例说明 四:优点 五:缺点 一:基本介绍 1)属于行为模式 2)如果我们的集合元素是用不同的方式实现的,有数组,还有java的集合类,或者还有其他方式,当客户 端要遍历这些集合元素的时候就要使用多种遍历方式,而且还会暴露元素的内部结构,可以…...
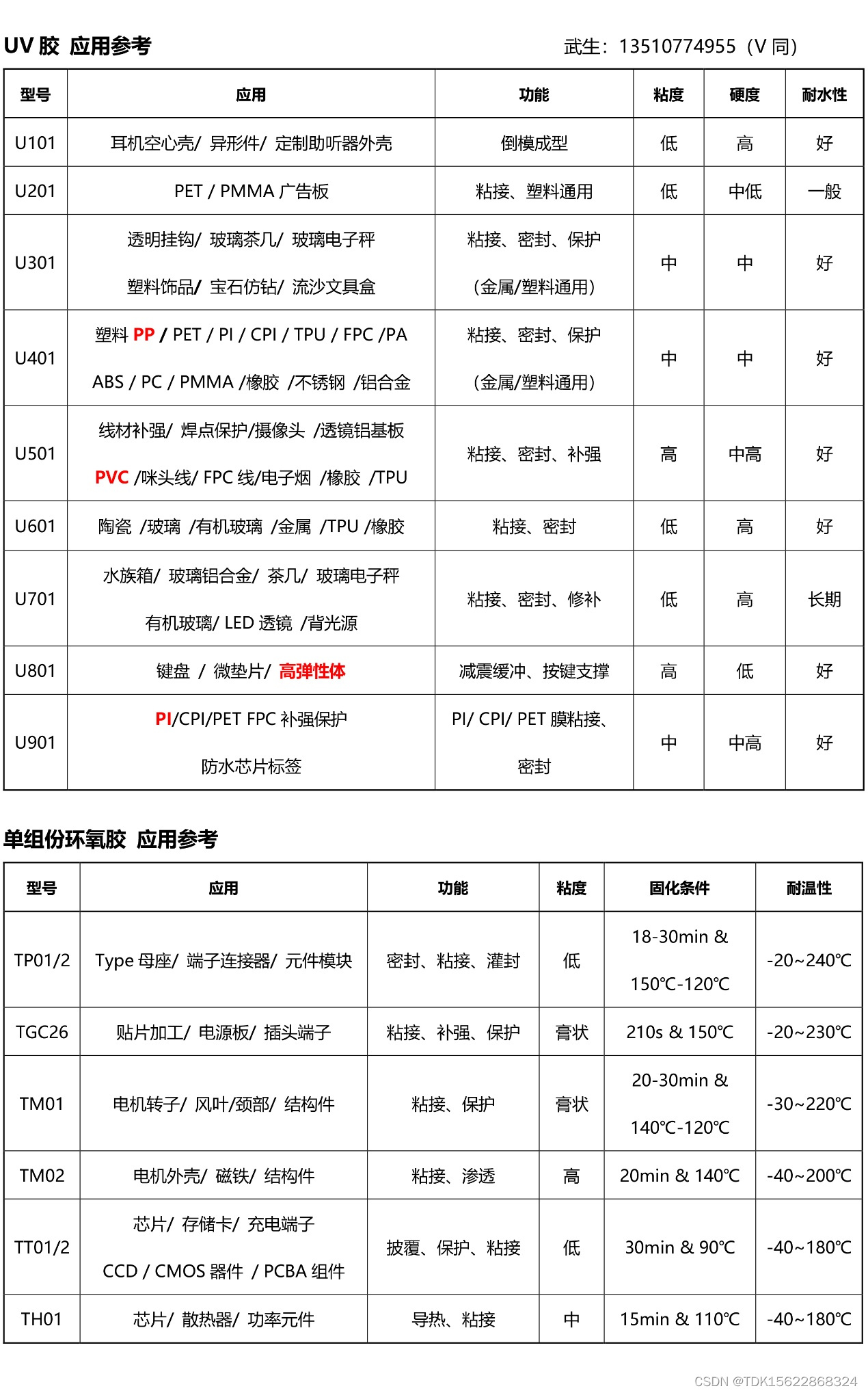
UV胶带和UV胶水的应用场景有哪些不同吗?
UV胶带和UV胶水的应用场景有哪些不同吗? UV胶带和UV胶水的应用场景确实存在不同之处,以下是详细的比较和归纳: 一:按使用场景来看: UV胶带的应用场景: 包装行业:UV胶带在包装行业中常用于食品包装、药…...

监控员工上网软件有哪些|4款好用的员工上网行为管理软件推荐
在当今数字化办公环境中,确保网络安全、提升工作效率、以及规范员工上网行为成为企业管理的重要组成部分。 为此,一套高效的员工上网行为管理软件显得尤为关键。 本文将为您推荐五款市场上广受好评的员工上网行为管理软件,帮助您有效监控与管…...

【IPython的使用技巧】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...
最新AI智能聊天对话问答系统源码(详细图文搭建部署教程)+AI绘画系统(Midjourney),DALL-E3文生图,TTS语音识别输入,文档分析
一、文章前言 随着人工智能技术的持续进步,AI绘画已经发展成为一个日益成熟的领域。越来越多的人开始尝试使用AI绘画软件来创作艺术作品。尽管这些AI绘画软件对绘画领域产生了显著影响,但它们并不会完全取代画师。与传统手绘不同,AI绘画可以…...

项目四 OpenStack身份管理
任务一 理解身份服务 1.1 •Keystone的基本概念 • 认证 ( Authentication ) —— 确认 用户身份的过程,又称身份验证 。 • 凭证 ( Credentials ) —— 又 称凭据,是用于确认用户身份的数据 。 • 令牌 …...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
