【数学】什么是方法矩估计?和最大似然估计是什么关系?
背景
方法矩估计(Method of Moments Estimation)和最大似然估计(Maximum Likelihood Estimation, MLE)是两种常用的参数估计方法。方法矩估计基于样本矩与总体矩的关系,通过样本数据计算样本矩来估计总体参数。最大似然估计基于最大化样本数据的联合概率密度函数,通过寻找参数值使得样本数据出现的概率最大来估计参数。
公式
方法矩估计
方法矩估计基于以下公式:
- 样本矩: M k = 1 n ∑ i = 1 n X i k M_k = \frac{1}{n} \sum_{i=1}^{n} X_i^k Mk=n1∑i=1nXik
- 总体矩: E ( X k ) = μ k E(X^k) = \mu_k E(Xk)=μk
通过设定样本矩等于总体矩,可以解出参数估计值。
最大似然估计
最大似然估计基于以下公式:
- 似然函数: L ( θ ) = ∏ i = 1 n f ( X i ; θ ) L(\theta) = \prod_{i=1}^{n} f(X_i; \theta) L(θ)=∏i=1nf(Xi;θ)
- 对数似然函数: ln L ( θ ) = ∑ i = 1 n ln f ( X i ; θ ) \ln L(\theta) = \sum_{i=1}^{n} \ln f(X_i; \theta) lnL(θ)=∑i=1nlnf(Xi;θ)
通过最大化对数似然函数来求解参数估计值。
示例题目
示例 1:正态分布参数估计
假设样本数据来自一个均值为 μ \mu μ,方差为 σ 2 \sigma^2 σ2的正态分布 N ( μ , σ 2 ) N(\mu, \sigma^2) N(μ,σ2),我们要估计 μ \mu μ和 σ 2 \sigma^2 σ2。
详细讲解
方法矩估计
-
样本矩计算:
- 一阶样本矩: M 1 = 1 n ∑ i = 1 n X i M_1 = \frac{1}{n} \sum_{i=1}^{n} X_i M1=n1∑i=1nXi
- 二阶样本矩: M 2 = 1 n ∑ i = 1 n X i 2 M_2 = \frac{1}{n} \sum_{i=1}^{n} X_i^2 M2=n1∑i=1nXi2
-
总体矩关系:
- 一阶总体矩: E ( X ) = μ E(X) = \mu E(X)=μ
- 二阶总体矩: E ( X 2 ) = μ 2 + σ 2 E(X^2) = \mu^2 + \sigma^2 E(X2)=μ2+σ2
-
通过样本矩等于总体矩,得到:
μ ^ = M 1 = 1 n ∑ i = 1 n X i \hat{\mu} = M_1 = \frac{1}{n} \sum_{i=1}^{n} X_i μ^=M1=n1i=1∑nXi
σ ^ 2 = M 2 − μ ^ 2 \hat{\sigma}^2 = M_2 - \hat{\mu}^2 σ^2=M2−μ^2
最大似然估计
-
似然函数:
L ( μ , σ 2 ) = ∏ i = 1 n 1 2 π σ 2 exp ( − ( X i − μ ) 2 2 σ 2 ) L(\mu, \sigma^2) = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(X_i - \mu)^2}{2\sigma^2} \right) L(μ,σ2)=i=1∏n2πσ21exp(−2σ2(Xi−μ)2) -
对数似然函数:
ln L ( μ , σ 2 ) = − n 2 ln ( 2 π σ 2 ) − 1 2 σ 2 ∑ i = 1 n ( X i − μ ) 2 \ln L(\mu, \sigma^2) = -\frac{n}{2} \ln(2\pi\sigma^2) - \frac{1}{2\sigma^2} \sum_{i=1}^{n} (X_i - \mu)^2 lnL(μ,σ2)=−2nln(2πσ2)−2σ21i=1∑n(Xi−μ)2 -
对 μ \mu μ和 σ 2 \sigma^2 σ2求导并设为0,解得:
μ ^ = 1 n ∑ i = 1 n X i \hat{\mu} = \frac{1}{n} \sum_{i=1}^{n} X_i μ^=n1i=1∑nXi
σ ^ 2 = 1 n ∑ i = 1 n ( X i − μ ^ ) 2 \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^{n} (X_i - \hat{\mu})^2 σ^2=n1i=1∑n(Xi−μ^)2
Python代码求解
import numpy as np# 生成样本数据
np.random.seed(0)
data = np.random.normal(loc=5, scale=2, size=100)# 方法矩估计
mu_mom = np.mean(data)
sigma2_mom = np.mean(data**2) - mu_mom**2# 最大似然估计
mu_mle = np.mean(data)
sigma2_mle = np.var(data, ddof=0)print("方法矩估计:")
print(f"mu = {mu_mom}, sigma^2 = {sigma2_mom}")print("最大似然估计:")
print(f"mu = {mu_mle}, sigma^2 = {sigma2_mle}")
实际生活中的例子
在金融领域中,投资组合的收益通常被假设为正态分布。为了估计未来收益的均值和波动率,金融分析师可以使用历史收益数据来进行参数估计。通过方法矩估计或最大似然估计,可以得出投资组合的均值收益和方差,从而指导投资决策。
方法矩估计与最大似然估计的关系与优缺点
两种方法各有优缺点:
- 方法矩估计通常计算简单,易于理解,但在有限样本量下估计量的效率较低。
- 最大似然估计在大样本量下具有一致性和渐近正态性,估计量更有效,但计算复杂,尤其是对于复杂模型。
选择哪种方法更好取决于具体问题和数据特点。一般情况下,最大似然估计更受欢迎,因为它在大样本下具有良好的统计性质。
相关文章:

【数学】什么是方法矩估计?和最大似然估计是什么关系?
背景 方法矩估计(Method of Moments Estimation)和最大似然估计(Maximum Likelihood Estimation, MLE)是两种常用的参数估计方法。方法矩估计基于样本矩与总体矩的关系,通过样本数据计算样本矩来估计总体参数。最大似…...

C++初学者指南第一步---10.内存(基础)
C初学者指南第一步—10.内存(基础) 文章目录 C初学者指南第一步---10.内存(基础)1.内存模型1.1 纸上谈兵:C的抽象内存模型1.2 实践:内存的实际处理 2. 自动存储3.动态存储:std::vector3.1 动态内…...

扩散模型详细推导过程——编码与解码
符号表 符号含义 x ( i ) z 0 ( i ) \boldsymbol{x}^{(i)}\boldsymbol{z}_0^{(i)} x(i)z0(i)第 i i i个训练数据,其为长度为 d d d的向量 z t ( i ) \boldsymbol{z}_t^{(i)} zt(i)第 i i i个训练数据在第 t t t时刻的加噪版本 ϵ t ( i ) \boldsymbol{\epsilo…...

js如何实现开屏弹窗
开屏弹窗是什么,其实就是第一次登录后进入页面给你的一种公告提示,此后再回到当前这个页面时弹窗是不会再出现的。也就是说这个弹窗只会出现一次。 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>…...

C#——文件读取Directory类详情
文件读取Directory类 Durectory提供了目录以及子目录进行创建移动和列举操作方法 Directory和Directorylnfo类(主要操作文件目录属性列如文件是否隐藏的 或者只读等这些属性) Directory对目录进行复制、移动、重命名、创建和删除等操作DirectoryInfo用于对目录属性执行操作 …...

Ruby on Rails Post项目设置网站初始界面
在构建了Ruby的Web服务器后,第三步就可以去掉框架的官方页面,设置自己的网页初始页了。 Linux系统安装Ruby语言-CSDN博客 、在Ubuntu中创建Ruby on Rails项目并搭建数据库-CSDN博客、 Ruby语言建立Web服务器-CSDN博客 了解Ruby onRails项目中的主要文件…...

03-QTWebEngine中使用qtvirtualkeyboard
qt提供了 virtualKeyboard 虚拟键盘模块,只需要在在main函数中最开始加入这样一句就可以了 qputenv("QT_IM_MODULE", QByteArray("qtvirtualkeyboard")); 但是在使用的时候遇到了一些问题: 1、中文输入的时候没有输入提示 Qvirt…...
)
leetcode3无重复字符的最长字串(重点讲滑动窗口)
本文主要讲解无重复字符的最长字串的要点与细节,根据步骤一步步走更方便理解 c与java代码如下,末尾 具体要点: 1. 区分一下子串和子序列 子串:要求元素在母串中是连续地出现 子序列:不要求连续 2. 题目中有两个核心…...
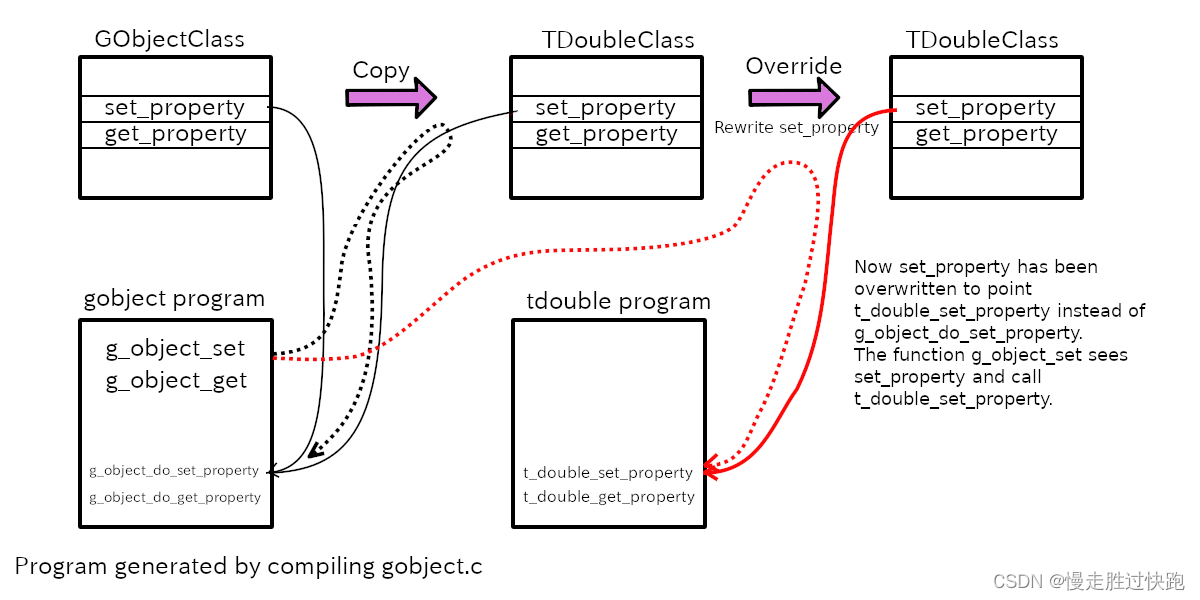
Gobject tutorial 八
The GObject base class Object memory management Gobject的内存管理相关的API很复杂,但其目标是提供一个基于引用计数的灵活的内存管理模式。 下面我们来介绍一下,与管理引用计数相关的函数。 Reference Count 函数g_object_ref和g_object_unref的…...

DDMA信号处理以及数据处理的流程---cfar检测
Hello,大家好,我是Xiaojie,好久不见,欢迎大家能够和Xiaojie一起学习毫米波雷达知识,Xiaojie准备连载一个系列的文章—DDMA信号处理以及数据处理的流程,本系列文章将从目标生成、信号仿真、测距、测速、cfar检测、测角、目标聚类、目标跟踪这几个模块逐步介绍,这个系列的…...
【机器学习】从理论到实践:决策树算法在机器学习中的应用与实现
📝个人主页:哈__ 期待您的关注 目录 📕引言 ⛓决策树的基本原理 1. 决策树的结构 2. 信息增益 熵的计算公式 信息增益的计算公式 3. 基尼指数 4. 决策树的构建 🤖决策树的代码实现 1. 数据准备 2. 决策树模型训练 3.…...

Zookeeper 集群节点故障剔除、切换、恢复原理
Zookeeper 集群节点故障剔除、切换、恢复原理 zookeeper 集群节点故障时,如何剔除节点,如果为领导节点如何处理,如何进行故障恢 复的,实现原理? 在 Zookeeper 集群中,当节点故障时,集群需要自动剔除故障节点并进行故障恢复,确保集群的高 可用性和一致性。具体来说,…...

解决帝国cms栏目管理拼音乱码的问题
帝国CMS7.5版本utf-8版网站后台增加栏目生成乱码的问题怎么解决 1、需要改一个函数,并且增加一个处理文件,方法如下: 修改e/class/connect.php文件,找到ReturnPinyinFun函数,如未修改文件在4533-4547行,将…...

Git快速入门
一 快速使用 1.1 初始化 什么是版本库呢?版本库又名仓库,可以简单理解成一个目录,这个目录里面的所有文件都可以被Git管理起来,每个文件的修改、删除,Git都能跟踪,以便任何时刻都可以追踪历史࿰…...

【18.0】JavaScript---事件案例
【18.0】JavaScript—事件案例 【一】开关灯事件 【介绍】设置一个按钮,按下按钮触发事件,来回切换圆形图片的颜色 【分析】 图片设置:设置成圆形的图片背景颜色:设置红绿两个颜色,来回切换按钮设置:点击…...
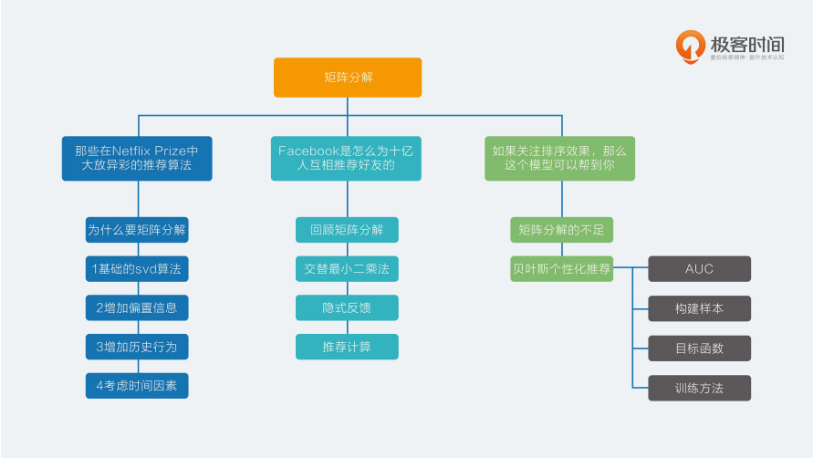
推荐系统三十六式学习笔记:原理篇.矩阵分解12|如果关注排序效果,那么这个模型可以帮到你
目录 矩阵分解的不足贝叶斯个性化排序AUC构造样本目标函数训练方法 总结 矩阵分解在推荐系统中的地位非常崇高。它既有协同过滤的血统,又有机器学习的基因,可以说是非常优秀了;但即便如此,传统的矩阵分解无论是在处理显式反馈&…...

Kafka之ISR机制的理解
文章目录 Kafka的基本概念什么是ISRISR的维护机制ISR的作用ISR相关配置参数同步过程示例代码总结 Kafka中的ISR(In-Sync Replicas同步副本)机制是确保数据高可用性和一致性的核心组件。 Kafka的基本概念 在Kafka中,数据被组织成主题…...
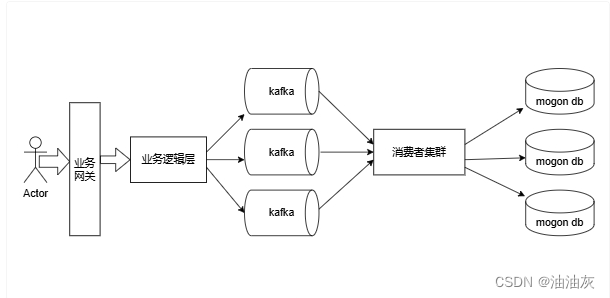
如何设计一个点赞系统
首先我们定义出一个点赞系统需要对外提供哪些接口: 1.用户对特定的消息进行点赞; 2.用户查看自己发布的某条消息点赞数量以及被哪些人赞过; 3.用户查看自己给哪些消息点赞过; 这里假设每条消息都有一个message_id, 每一个用户都…...

对象存储测试工具-s3cmd
一、环境安装 官网:https://s3tools.org/s3cmd 下载安装包:https://s3tools.org/download GitHub:https://github.com/s3tools/s3cmd/releases 本文安装包:https://github.com/s3tools/s3cmd/releases/download/v2.0.2/s3cmd-2.0…...

OpenCV--图像色彩空间及转换
图像色彩空间及转换 python代码和笔记 python代码和笔记 import cv2 色彩空间,基础:RGB或BGR OpenCV中: 一、HSV(HSB):用的最多, Hue:色相-色彩(0-360),红色:0,绿色&…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
