【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 披萨大作战(100分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员
✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解
💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导
👏 感谢大家的订阅➕ 和 喜欢💗
📎在线评测链接
https://app5938.acapp.acwing.com.cn/contest/2/problem/OD1067
🌍 评测功能需要 ⇒ 订阅专栏 ⇐ 后私信联系清隆解锁~
🍓OJ题目截图
文章目录
- 📎在线评测链接
- 🍓OJ题目截图
- 🥧 披萨大作战
- 题目描述
- 输入格式
- 输出格式
- 样例输入
- 样例输出
- 数据范围
- 题解
- 参考代码
🥧 披萨大作战
题目描述
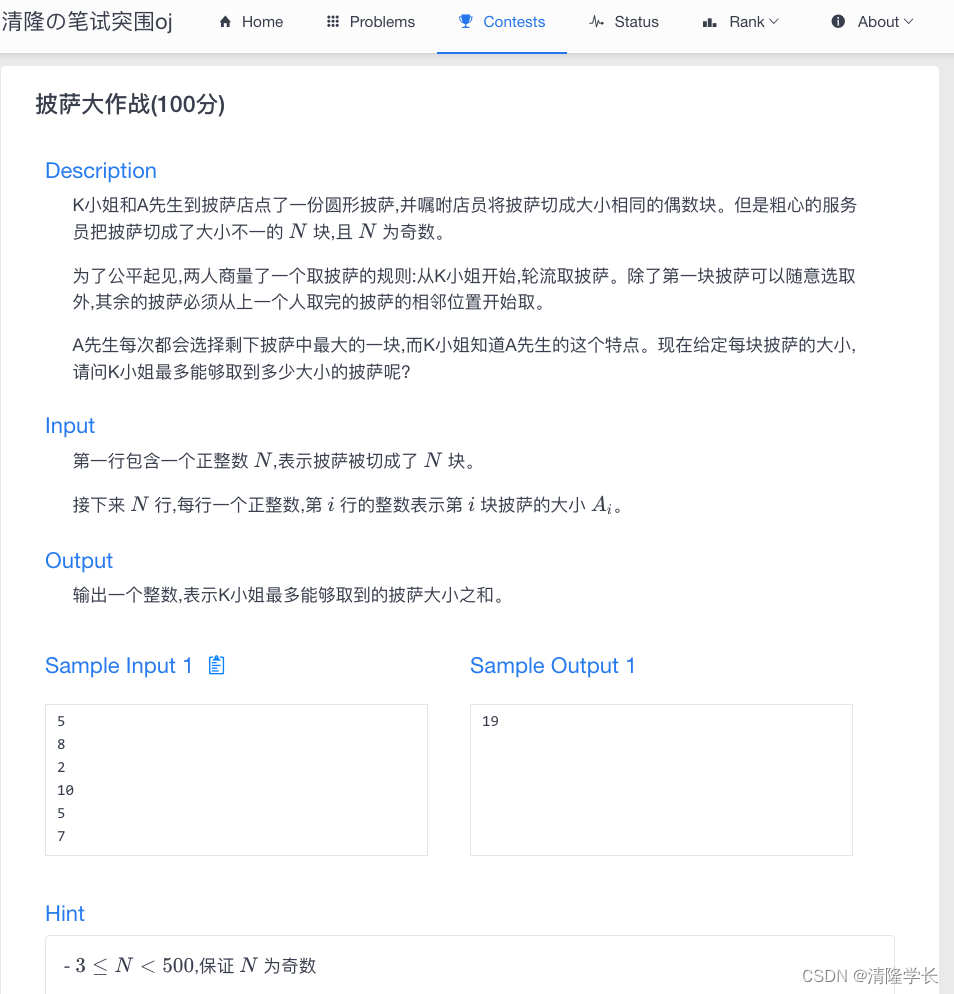
K小姐和A先生到披萨店点了一份圆形披萨,并嘱咐店员将披萨切成大小相同的偶数块。但是粗心的服务员把披萨切成了大小不一的 N N N 块,且 N N N 为奇数。
为了公平起见,两人商量了一个取披萨的规则:从K小姐开始,轮流取披萨。除了第一块披萨可以随意选取外,其余的披萨必须从上一个人取完的披萨的相邻位置开始取。
A先生每次都会选择剩下披萨中最大的一块,而K小姐知道A先生的这个特点。现在给定每块披萨的大小,请问K小姐最多能够取到多少大小的披萨呢?
输入格式
第一行包含一个正整数 N N N,表示披萨被切成了 N N N 块。
接下来 N N N 行,每行一个正整数,第 i i i 行的整数表示第 i i i 块披萨的大小 A i A_i Ai。
输出格式
输出一个整数,表示K小姐最多能够取到的披萨大小之和。
样例输入
5
8
2
10
5
7
样例输出
19
数据范围
- 3 ≤ N < 500 3 \le N < 500 3≤N<500,保证 N N N 为奇数
- 1 ≤ A i ≤ 2147483647 1 \le A_i \le 2147483647 1≤Ai≤2147483647
题解
本题可以使用记忆化搜索来解决。
定义 s o l v e ( L , R ) solve(L,R) solve(L,R) 表示当前还剩下第 L L L 块到第 R R R 块披萨时,K小姐能够取到的最大披萨大小之和。那么答案就是 m a x ( s o l v e ( ( i + 1 ) m o d N , ( i − 1 + N ) m o d N ) + A i ) max(solve((i+1) \bmod N, (i-1+N) \bmod N) + A_i) max(solve((i+1)modN,(i−1+N)modN)+Ai),其中 0 ≤ i < N 0 \le i < N 0≤i<N。
对于函数 s o l v e ( L , R ) solve(L,R) solve(L,R),我们可以分情况讨论:
-
如果 L = R L = R L=R,那么只剩下一块披萨,K小姐直接取走,因此 s o l v e ( L , R ) = A L solve(L,R) = A_L solve(L,R)=AL。
-
如果 L ≠ R L \neq R L=R,那么A先生会取走两端披萨中较大的一块。设 L ′ L' L′ 和 R ′ R' R′ 分别表示取走披萨后的左右端点,那么有:
- 如果 A L > A R A_L > A_R AL>AR,那么 L ′ = ( L + 1 ) m o d N , R ′ = R L' = (L+1) \bmod N, R' = R L′=(L+1)modN,R′=R
- 如果 A L ≤ A R A_L \le A_R AL≤AR,那么 L ′ = L , R ′ = ( R − 1 + N ) m o d N L' = L, R' = (R-1+N) \bmod N L′=L,R′=(R−1+N)modN
因此 s o l v e ( L , R ) = m a x ( A L + s o l v e ( L ′ , R ) , A R + s o l v e ( L , R ′ ) ) solve(L,R) = max(A_L + solve(L', R), A_R + solve(L, R')) solve(L,R)=max(AL+solve(L′,R),AR+solve(L,R′))。
为了避免重复计算,我们可以使用记忆化数组 d p dp dp 来保存已经计算过的状态。其中 d p [ i ] [ j ] dp[i][j] dp[i][j] 表示当前还剩下第 i i i 块到第 j j j 块披萨时,K小姐能够取到的最大披萨大小之和。
时间复杂度 O ( N 2 ) O(N^2) O(N2),空间复杂度 O ( N 2 ) O(N^2) O(N2)。
参考代码
- Python
N = int(input())
A = [int(input()) for _ in range(N)]
dp = [[-1] * N for _ in range(N)]def solve(L, R):if A[L] > A[R]:L = (L + 1) % Nelse:R = (R - 1 + N) % Nif dp[L][R] != -1:return dp[L][R]if L == R:dp[L][R] = A[L]else:dp[L][R] = max(A[L] + solve((L+1)%N, R), A[R] + solve(L, (R-1+N)%N))return dp[L][R]ans = 0
for i in range(N):ans = max(ans, solve((i+1)%N, (i-1+N)%N) + A[i])print(ans)
- Java
import java.util.Scanner;public class Main {static int N;static int[] A;static int[][] dp;public static void main(String[] args) {Scanner sc = new Scanner(System.in);N = sc.nextInt();A = new int[N];for (int i = 0; i < N; i++) {A[i] = sc.nextInt();}dp = new int[N][N];for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {dp[i][j] = -1;}}int ans = 0;for (int i = 0; i < N; i++) {ans = Math.max(ans, solve((i+1)%N, (i-1+N)%N) + A[i]);}System.out.println(ans);}static int solve(int L, int R) {if (A[L] > A[R]) {L = (L + 1) % N;} else {R = (R - 1 + N) % N;}if (dp[L][R] != -1) {return dp[L][R];}if (L == R) {dp[L][R] = A[L];} else {dp[L][R] = Math.max(A[L] + solve((L+1)%N, R), A[R] + solve(L, (R-1+N)%N));}return dp[L][R];}
}
- Cpp
#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;const int N = 500;
int n, a[N], dp[N][N];int solve(int L, int R) {if (a[L] > a[R]) {L = (L + 1) % n;} else {R = (R - 1 + n) % n;}if (dp[L][R] != -1) {return dp[L][R];}if (L == R) {dp[L][R] = a[L];} else {dp[L][R] = max(a[L] + solve((L+1)%n, R), a[R] + solve(L, (R-1+n)%n));}return dp[L][R];
}int main() {cin >> n;for (int i = 0; i < n; i++) {cin >> a[i];}memset(dp, -1, sizeof(dp));int ans = 0;for (int i = 0; i < n; i++) {ans = max(ans, solve((i+1)%n, (i-1+n)%n) + a[i]);}cout << ans << endl;return 0;
}
相关文章:

【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 披萨大作战(100分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 …...

探索Facebook对世界各地文化的影响
随着数字化时代的到来,社交媒体已成为连接世界各地人们的重要平台之一。而在这个领域的巨头之一,Facebook不仅是人们沟通交流的场所,更是一座桥梁,将不同地域、文化的人们联系在一起。本文将探索Facebook对世界各地文化的影响&…...

导出requirements.txt
文章目录 requirements.txt导出环境中所有包导出当前项目的包可能遇到的问题 requirements.txt 在Python项目中,通常使用requirements.txt文件来列出所有需要的第三方库和模块。这个文件通常位于项目的根目录下,并且在安装Python项目时,可以…...
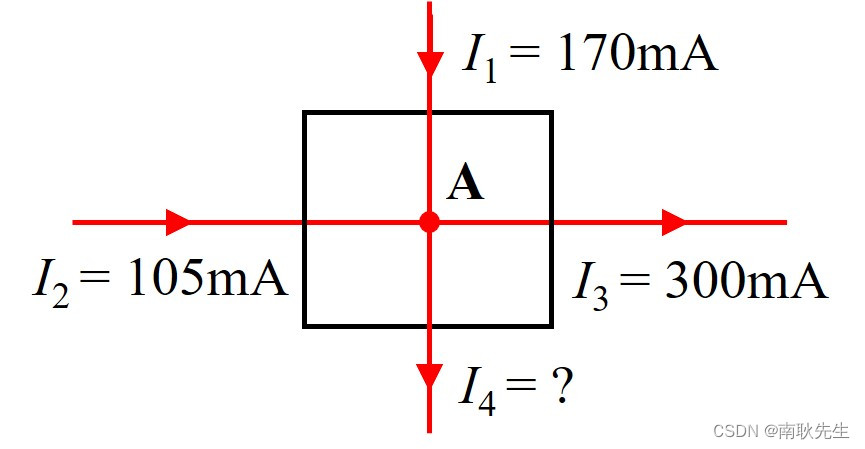
我主编的电子技术实验手册(09)——并联电路
本专栏是笔者主编教材(图0所示)的电子版,依托简易的元器件和仪表安排了30多个实验,主要面向经费不太充足的中高职院校。每个实验都安排了必不可少的【预习知识】,精心设计的【实验步骤】,全面丰富的【思考习…...

数据结构_二叉树
目录 一、树型结构 二、二叉树 2.1 概念 2.2 特殊的二叉树 2.3 二叉树的性质 2.4 二叉树的存储 2.5 遍历二叉树 2.6 操作二叉树 总结 一、树型结构 树是一种非线性的数据结构,它是由 n(n>0) 个有限结点组成一个具有层次关系的集合,一棵 n 个…...

Java线程池七个参数详解
ThreadPoolExecutor 是JDK中的线程池实现,这个类实现了一个线程池需要的各个方法,它提供了任务提交、线程管理、监控等方法 下面是 ThreadPoolExecutor 类的构造方法源码,其他创建线程池的方法最终都会导向这个构造方法,共有7个参…...
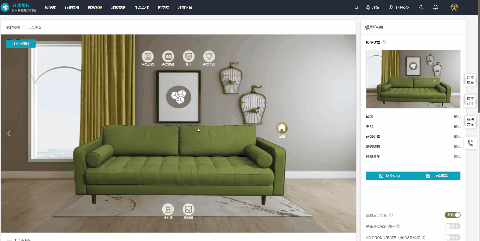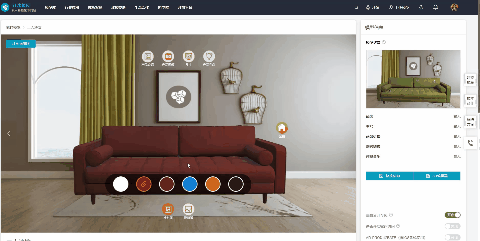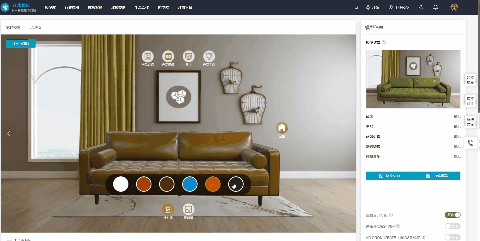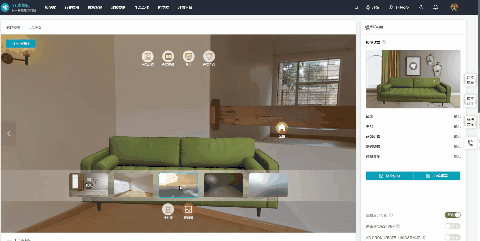
产品Web3D交互展示有什么优势?如何快速制作?
智能互联网时代,传统的图片、文字、视频等产品展示方式,因为缺少互动性,很难引起用户的兴趣,已经逐渐失去了宣传优势。 Web3D交互展示技术的出现,让众多品牌和企业找到了新的方向,线上产品展示不在枯燥无趣…...

Python | Leetcode Python题解之第171题Excel列表序号
题目: 题解: class Solution:def titleToNumber(self, columnTitle: str) -> int:number, multiple 0, 1for i in range(len(columnTitle) - 1, -1, -1):k ord(columnTitle[i]) - ord("A") 1number k * multiplemultiple * 26return n…...
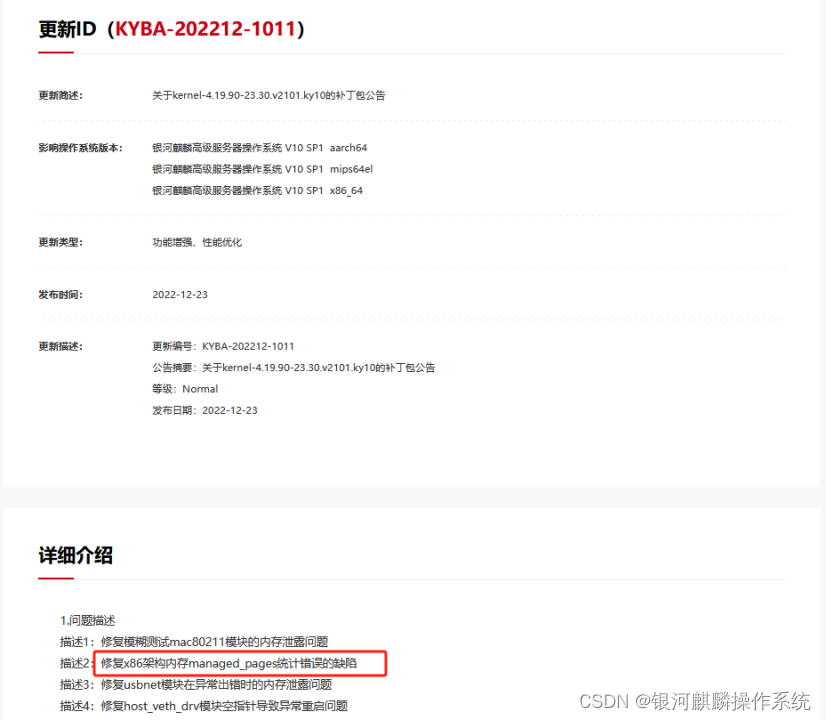
【银河麒麟】高可用触发服务器异常重启,处理机制详解
1.服务器环境以及配置 【机型】物理机 处理器: Intel 内存: 126G 【内核版本】 4.19.90-25.16.v2101.ky10.x86_64 【银河麒麟操作系统镜像版本】 Kylin-Server-10-SP2-Release-Shenzhen-Metro-x86-Build01-20220619 Kylin-HA-10-SP2-Release-S…...
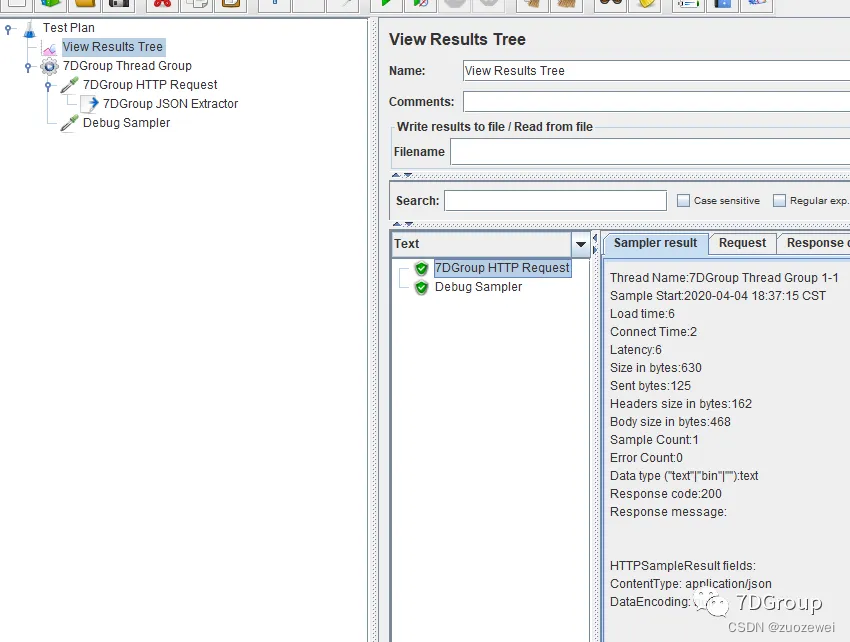
性能工具之 JMeter 常用组件介绍(七)
文章目录 一、后置处理器1、Regular Expression Extractor(正则表达式提取器)2、JSON Extractor(JSON表达式提取器)3、Regular Expression Extractor(正则表达式提取器) 二、小结 本文主要介绍JMeter主流后置处理器的功能 一、后置处理器 从上面可以看出后置处理可以插件挺多&a…...
Python学习笔记15:进阶篇(四)文件的读写。
文件操作 学习编程操作中,我觉得文件操作是必不可少的一部分。不管是读书的时候学习的c,c,工作的前学的java,现在学的Python,没学过的php和go,都有文件操作的模块以及库的支持,重要性毫无疑问。…...

角度调制与解调电路
music! (黄佳庆老师可爱捏) 调角 角度调制有较好的抗噪性能。 调相 相位变化的频率变化的微分,频率变化是相位变化的积分 相位的变化率就是频率 调频 调相与调频的关系 大F是输入信号的频率,大Ω是输入信号的角频率 …...
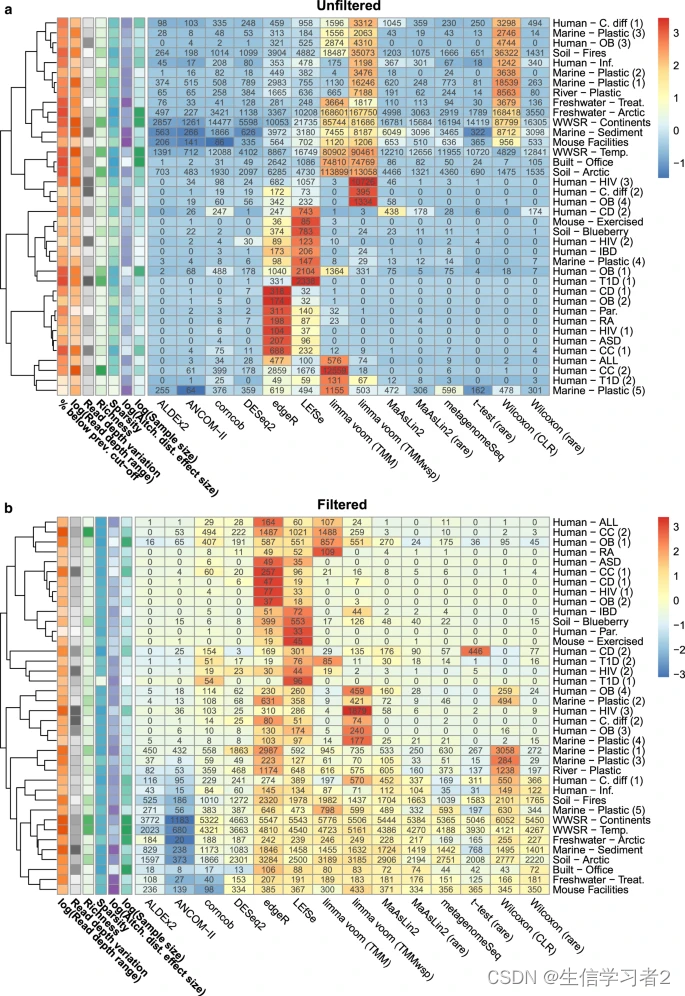
数据分析:微生物组差异丰度方法汇总
欢迎大家关注全网生信学习者系列: WX公zhong号:生信学习者Xiao hong书:生信学习者知hu:生信学习者CDSN:生信学习者2 介绍 微生物数据具有一下的特点,这使得在做差异分析的时候需要考虑到更多的问题&…...

Linux驱动开发(二)--字符设备驱动开发提升 LED驱动开发实验
1、地址映射 在编写驱动之前,需要知道MMU,也就是内存管理单元,在老版本的 Linux 中要求处理器必须有 MMU,但是现在Linux 内核已经支持无 MMU 的处理器了。 MMU的功能如下: 完成虚拟空间到物理空间的映射 内存保护&…...
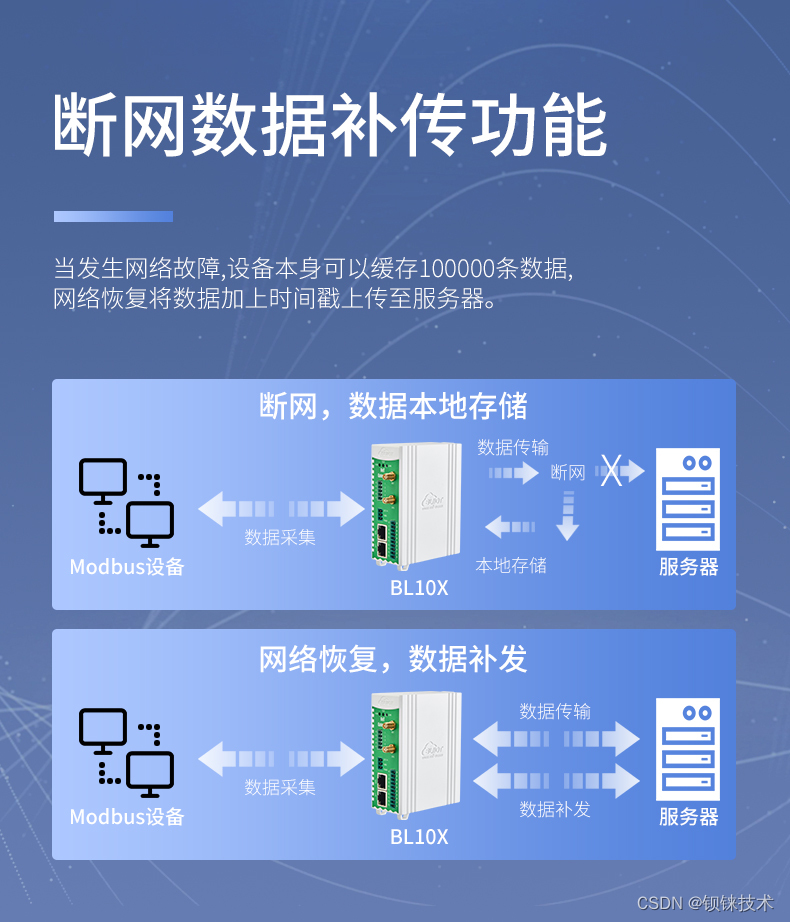
钡铼BL101网关助力智慧城市路灯远程智能管控
在迈向智慧城市的征途中,基础设施的智能化改造是关键一环,而路灯作为城市脉络的照明灯塔,其智能化升级对于节能减排、提升城市管理效率具有重要意义。钡铼BL101网关,作为Modbus转MQTT的专业桥梁,正以其卓越的性能和广泛…...
如何优雅的使用Github Action服务来将Hexo部署到Github Pages
文章目录 参考文章前提条件1. 初始化Hexo2. 初始化仓库3. 创建Token4. 修改_config.yml5. 配置Github Action工作流6. 推送验证7. 配置Github Pages8. 修改Hexo主题样式10. 添加文章遇到了一些问题和方案1. 网站没有样式问题2. 图片不显示 参考文章 Bilibili视频教程-9分钟零成…...

After Effects 2024 mac/win版:创意视效,梦想起航
After Effects 2024是一款引领视效革命的专业软件,汇聚了创意与技术的精华。作为Adobe推出的全新版本,它以其强大的视频处理和动画创作能力,成为从事设计和视频特技的机构,如电视台、动画制作公司、个人后期制作工作室以及多媒体工…...

信息打点web篇----web后端源码专项收集
前言 欢迎来到我的博客 个人主页:北岭敲键盘的荒漠猫-CSDN博客 专栏描述:因为第一遍过信息收集的时候,没怎么把收集做回事 导致后来在实战中,遭遇资产获取少,可渗透点少的痛苦,如今决定 从头来过,全面全方位…...

ArcGIS批量投影转换的妙用(地理坐标系转换为平面坐标系)
点击下方全系列课程学习 点击学习—>ArcGIS全系列实战视频教程——9个单一课程组合系列直播回放 这次文章我们来介绍一下,如何巧妙用要素数据集来实现要素的批量投影。不需要ArcGIS的模型构建器与解决。 例如,有多个要素要将CGCS_2000地理坐标系投…...

YOLOv10训练自己的数据集(图像目标检测)
目录 1、下载代码 2、环境配置 3、准备数据集 4、yolov10训练 可能会出现报错: 1、下载代码 源码地址:https://github.com/THU-MIG/yolov10 2、环境配置 打开源代码,在Terminal中,使用conda 创建虚拟环境配置 命令如下&a…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
