三角形法恢复空间点深度
三角形法恢复空间点深度
如下图,以图 I 1 I_1 I1为参考,图 I 2 I_2 I2的变换矩阵为 T T T。相机光心为 O 1 O_1 O1和 O 2 O_2 O2。在图 I 1 I_1 I1中有特征点 p 1 p_1 p1,对应图 I 2 I_2 I2中有特征点 p 2 p_2 p2。理论上直线 O 1 p 1 O_1p_1 O1p1 与 O 2 p 2 O_2p_2 O2p2 在场景中会相交于一点 P P P,该点即是两个特征点所对应的地图点在三维场景中的位置。(由于噪声的影响,这两条直线往往无法相交)。简言之,在已知两个相机的相对位姿的情况下,得到在两个视图下的对应匹配点,即可求得该对应点在空间中的位置,也就是求得图像点的深度
参考链接1 、参考链接2 、论文链接

1.求解空间点坐标
当我们得到两个视图的一组匹配点,我们希望能恢复出世界点在三维世界的坐标。这里就涉及到使用三角形法来恢复点在3D空间的结构。一般比较常用的方法是线性三角形法(Linear triangulation methods )。线性三角形法使用直接线性变化(DLT)对点的世界坐标进行求解。
已知点对和和两个图像的投影矩阵和 ,根据相机投影模型,对应3D点满足 :
{ x 1 = P 1 X x 2 = P 2 X \begin{cases} \mathbf x_1 = P_1 \mathbf X \\ \mathbf x_2= P_2\mathbf X \end{cases} {x1=P1Xx2=P2X
这里 x 1 x_1 x1、 x 2 x_2 x2是归一化后特征点坐标, X X X为三维空间点在世界坐标系的齐次坐标 X = [ x y z 1 ] T X=\begin{matrix} [x & y &z &1]^T \end{matrix} X=[xyz1]T使用DLT需要把式子改变成的形式。由于是齐次坐标的表示形式,使用叉乘消去齐次因子,有
{ x 1 × ( P 1 X ) = 0 x 2 × ( P 2 X ) = 0 \begin{cases} \mathbf x_1 \times (P_1 \mathbf X) = \mathbf 0 \\ \mathbf x_2 \times (P_2\mathbf X)=\mathbf 0 \end{cases} {x1×(P1X)=0x2×(P2X)=0
把和按照行展开代入,对第一幅图 I 1 I_1 I1有
[ 0 − 1 y 1 1 0 − x 1 − y 1 x 1 0 ] [ P 1 1 T X P 1 2 T X P 1 3 T X ] = 0 \begin{bmatrix} 0 & -1 & y_1\\ 1 & 0 & -x_1\\ -y_1 & x_1 & 0 \end{bmatrix} \begin{bmatrix} P^{1T}_1X\\P^{2T}_1X\\P^{3T}_1X \end{bmatrix} = 0 01−y1−10x1y1−x10 P11TXP12TXP13TX =0
即
x 1 ( P 1 3 T X ) − ( P 1 1 T X ) = 0 y 1 ( P 1 3 T X ) − ( P 1 2 T X ) = 0 x 1 ( P 1 2 T X ) − y 1 ( P 1 1 T X ) = 0 \begin{split} x_1(P^{3T}_1X)-(P^{1T}_1X)=0\\ y_1(P^{3T}_1X)-(P^{2T}_1X)=0\\ x_1(P^{2T}_1X)-y_1(P^{1T}_1X)=0\\ \end{split} x1(P13TX)−(P11TX)=0y1(P13TX)−(P12TX)=0x1(P12TX)−y1(P11TX)=0
由此可以得到三个方程,由于第三个方程可以由前两个方程得到(第三个方程可由前两个方程线性表示),因此只需要考虑前两个方程。每对匹配的特征( x 1 x_1 x1和 x 2 x_2 x2)都会得到四个方程,表示为 A X = 0 AX =0 AX=0 的形式:
A = [ x 1 P 1 3 T − P 1 1 T y 1 P 1 3 T − P 1 2 T x 2 P 2 3 T − P 2 1 T y 2 P 2 3 T − P 2 2 T ] A =\begin{bmatrix} x_1P_1^{3T}-P^{1T}_1\\ y_1P_1^{3T}-P_1^{2T}\\ x_2P_2^{3T}-P_2^{1T}\\ y_2P_2^{3T}-P_2^{2T}\\ \end{bmatrix} A= x1P13T−P11Ty1P13T−P12Tx2P23T−P21Ty2P23T−P22T
由于是自由度为3的齐次方程,所以这是一个冗余的方程,这里相当于解一个线性最小二乘问题。方程的解为的最小奇异值对应的单位奇异矢量,解得,则最后令缩放使得的最后一项为1即可得到我们所求的3D点的坐标。
VINS-Mono 中的三角形法的实现代码如下:
/*** @description: DLT 三角形法恢复空间点深度* @date: 2024/06/20* @param[i]: Pose0: 第1帧 pose* @param[i]: Pose1: 第2帧 pose* @param[i]: point1: 第一帧 uv 坐标* @param[i]: point2: 第二帧 uv 坐标* @param[o]: point_3d: 三角化得到的三维坐标
**/
void GlobalSFM::triangulatePoint(Eigen::Matrix<double, 3, 4> &Pose0, Eigen::Matrix<double, 3, 4> &Pose1,Vector2d &point0, Vector2d &point1, Vector3d &point_3d)
{Matrix4d design_matrix = Matrix4d::Zero();design_matrix.row(0) = point0[0] * Pose0.row(2) - Pose0.row(0);design_matrix.row(1) = point0[1] * Pose0.row(2) - Pose0.row(1);design_matrix.row(2) = point1[0] * Pose1.row(2) - Pose1.row(0);design_matrix.row(3) = point1[1] * Pose1.row(2) - Pose1.row(1);Vector4d triangulated_point;triangulated_point =design_matrix.jacobiSvd(Eigen::ComputeFullV).matrixV().rightCols<1>();point_3d(0) = triangulated_point(0) / triangulated_point(3);point_3d(1) = triangulated_point(1) / triangulated_point(3);point_3d(2) = triangulated_point(2) / triangulated_point(3);
}
ORB-SLAM2中的三角形法的实现代码如下:
void Initializer::Triangulate(const cv::KeyPoint &kp1, const cv::KeyPoint &kp2, const cv::Mat &P1, const cv::Mat &P2, cv::Mat &x3D)
{cv::Mat A(4,4,CV_32F);A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0);A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1);A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0);A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1);cv::Mat u,w,vt;cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);x3D = vt.row(3).t();x3D = x3D.rowRange(0,3)/x3D.at<float>(3);
}
相关文章:

三角形法恢复空间点深度
三角形法恢复空间点深度 如下图,以图 I 1 I_1 I1为参考,图 I 2 I_2 I2的变换矩阵为 T T T。相机光心为 O 1 O_1 O1和 O 2 O_2 O2。在图 I 1 I_1 I1中有特征点 p 1 p_1 p1,对应图 I 2 I_2 I2中有特征点 p 2 p_2 p2。理论上直…...

Linux 阻塞和非阻塞 IO 实验学习
Linux 阻塞和非阻塞 IO 实验学习 IO 指的是 Input/Output,也就是输入/输出,是应用程序对驱动设备的输入/输出操作。当应用程序对设备驱动进行操作的时候,如果不能获取到设备资源,那么阻塞式 IO 就会将应用程序对应的线程挂起&…...

JuiceFS 社区版 v1.2 发布,新增企业级权限管理、平滑升级功能
JuiceFS 社区版 v1.2 今天正式发布,这是自 2021 年开源以来的第三个大版本。v1.2 也是一个长期支持版本(LTS)。我们将持续维护 v1.2 以及 v1.1 这两个版本,v1.0 将停止更新。 JuiceFS 是为云环境设计的分布式文件系统,…...

虚拟3D沉浸式展会编辑平台降低了线上办展的门槛
在数字化浪潮的引领下,VR虚拟网上展会正逐渐成为企业展示品牌实力、吸引潜在客户的首选平台。我们与广交会携手走过三年多的时光,凭借优质的服务和丰富的经验,赢得了客户的广泛赞誉。 面对传统展会活动繁多、企业运营繁忙的挑战,许…...

泛微E9开发 查询页面添加按钮,完成特定功能
查询页面添加按钮,完成特定功能 1、关联知识(查询页面实现新增按钮)2、功能实现2.1. 点击按钮,输出选中的checkbox的值2.2. 点击按钮,打开一个自定义对话框 3、实现方法 1、关联知识(查询页面实现新增按钮&…...
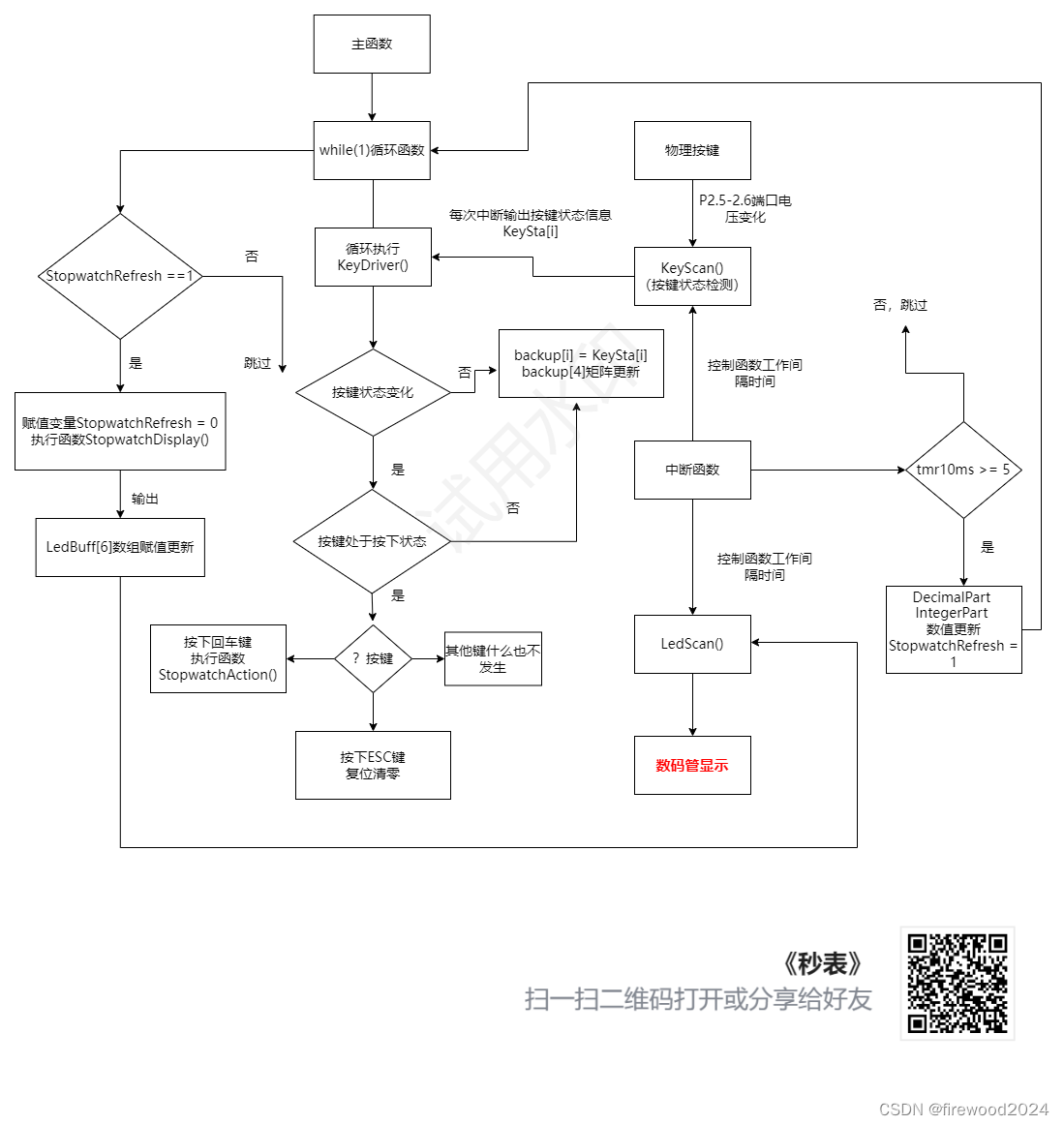
初学51单片机之数字秒表
不同数据类型间的相互转换 在C语言中,不同数据类型之间是可以混合运算的。当表达式中的数据类型不一致时,首先转换为同一类型,然后再进行计算。C语言有两种方式实现类型转换。一是自动类型转换,另外一种是强制类型转换。 转换的主…...
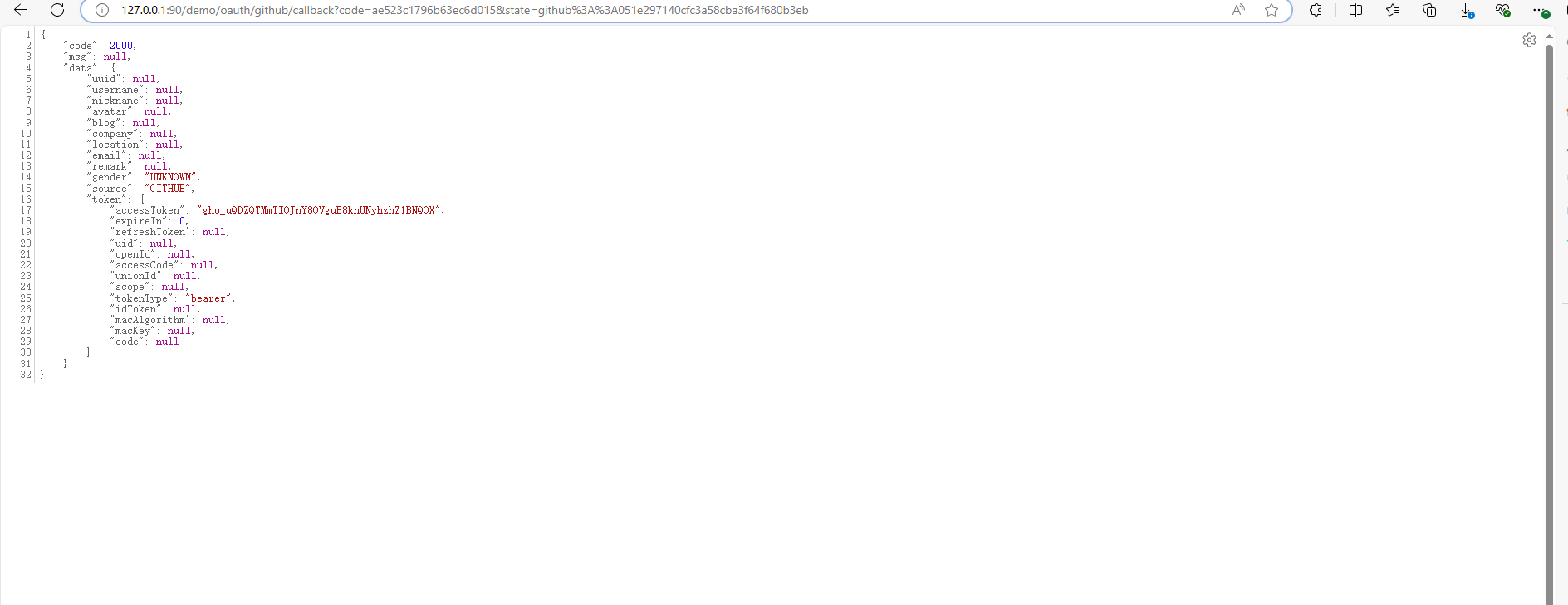
SpringBoot整合justauth实现多种方式的第三方登陆
目录 0.准备工作 1.引入依赖 2.yml文件 3. Controller代码 4.效果 参考 0.准备工作 你需要获取三方登陆的client-id和client-secret 以github为例 申请地址:Sign in to GitHub GitHub 1.引入依赖 <?xml version"1.0" encoding"UTF-8&quo…...

【Java算法】滑动窗口
🔥个人主页: 中草药 🔥专栏:【算法工作坊】算法实战揭秘 👖一. 长度最小的子数组 题目链接:209.长度最小的子数组 算法原理 滑动窗口 滑动窗口算法常用于处理数组/字符串等序列问题,通过定义一…...

C# —— 属性和字段
属性和字段的区别 1.都是定义在一个类中,属于类成员变量 2.字段一般都是私有的private,属性一般是公开的Public 3.字段以小驼峰命名方式 age,属性一般是以大驼峰命名 Age 4.字段可以存储数据,属性不能存储数据,通过属性…...

【计算机视觉】人脸算法之图像处理基础知识(四)
图像的几何变换 图像的几何变换是指在不改变图像内容的前提下对图像的像素进行空间几何变换。主要包括图像的平移变换、镜像变换、缩放和旋转等。 1.插值算法 插值通常用来放缩图像大小,在图像处理中常见的插值算法有最邻近插值法、双线性插值法、二次立方、三次…...

探索 Spring Boot 集成缓存功能的最佳实践
在线工具站 推荐一个程序员在线工具站:程序员常用工具(http://cxytools.com),有时间戳、JSON格式化、文本对比、HASH生成、UUID生成等常用工具,效率加倍嘎嘎好用。 程序员资料站 推荐一个程序员编程资料站:…...

微信小程序使用方法
一.在网页注册小程序账号(在未注册的情况下) 1.如果你还没有微信公众平台的账号,请先进入微信公众平台首页,点击 “立即注册” 按钮进行注册。我们选择 “小程序” 即可。 接着填写账号信息,需要注意的是,…...

前后端分离的后台管理系统源码,快速开发OA、CMS网站后台管理、毕业设计项目
那有没有一款软件解-决这种现状呢?答案是肯定的。引入我们的软件——eladmin。 介绍 ELADMIN,一个简单且易上手的 Spring boot 后台管理框架,已发布 Mybatis-Plus 版本,为开发者提供了一个全-面、高-效的解-决方案。 特点 高-效率:前后端完全分离,项目简单可配,内置代码…...

[深度学习]--分类问题的排查错误的流程
原因复现: 原生的.pt 好使, 转化后的 CoreML不好使, 分类有问题。 yolov8 格式的支持情况 Format Argument Suffix CPU GPU 0 PyTorch - .pt True True 1 Tor…...

微信小程序简易录音机
首先先创建一个项目(想必大家都会啦那就直接开干) 首先上html结构 <view class"wx-container"><view id"title">录音机</view><view id"time">{{hours}}:{{minute}}:{{second}}</view>&l…...

Ollama深度探索:AI大模型本地部署的全面教程
目录 引言一、Ollama概述1、定义与定位2、核心功能3、技术优势4、应用场景 二、安装与配置1、系统要求2、安装方法3、配置指南4、启动Ollama服务 四、快速开始1、启动Ollama2、部署运行模型3、REEST API 五、自定义模型1、定制化的必要性2、使用Modelfile定制模型3、参数调整4、…...

文心一言 VS 讯飞星火 VS chatgpt (285)-- 算法导论21.2 4题
四、请给出图 21-3 所示操作序列的一个运行时间的渐近紧确界,假定使用链表表示和加权合并启发式策略。如果要写代码,请用go语言。 文心一言: 图 21-3 没有直接给出,但通常这种操作序列可能与某种数据结构(如并查集或…...
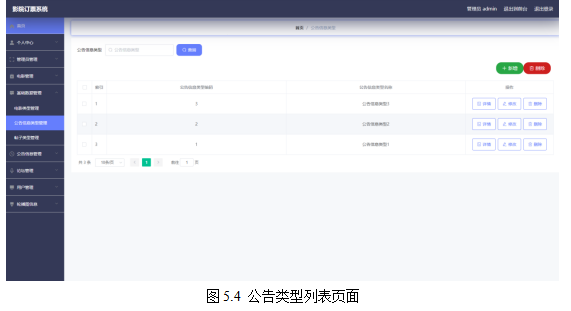
基于springboot实现影院订票系统项目【项目源码+论文说明】计算机毕业设计
基于springboot实现影院订票系统演示 摘要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本影院订票系统就是在这样的大环境下诞生,其可以帮助管理者在…...

Linux 常用命令合集
进入root模式 su -> 回车 -> 输入root用户密码关闭系统 方法1: shutdown -h now 方法2: init 0 方法3: telinit 0按预定时间关闭系统 shutdown -h hours:minutes &取消按预定时间关闭系统 shutdown -c重启 shutdown -r now重启…...
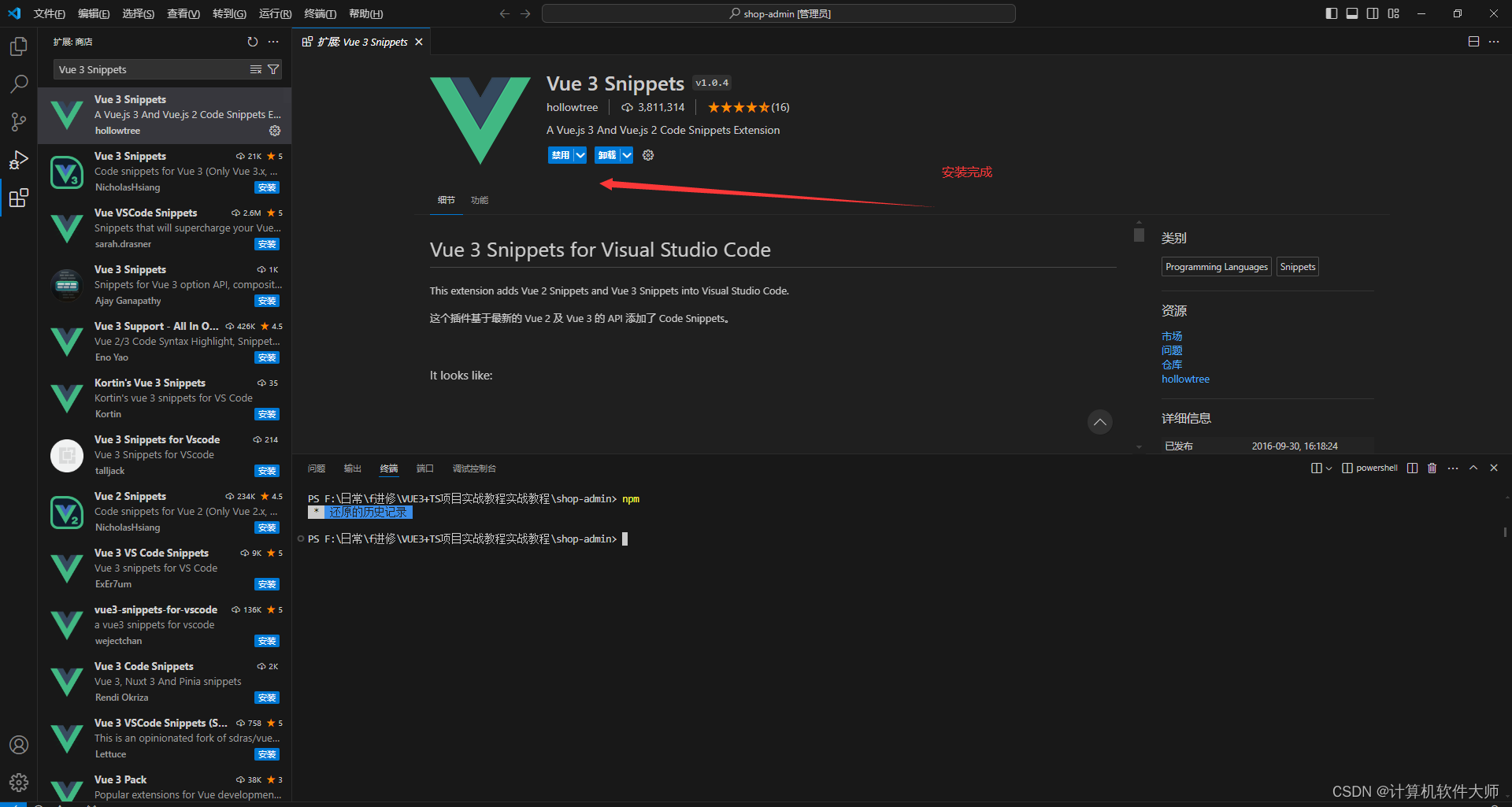
Vue3插件安装
一、volar插件安装 volar:Vue文件的语法提示和高亮提醒。volar已经更名为Vue - Official,其安装步骤如下。 (1)打开vscode,点击扩展面板,在搜索窗口中输入volar,选择Vue - Official进行安装。 (2࿰…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
