Vue57-组件的自定义事件_解绑
- 给谁绑的自定义事件,就找谁去触发;
- 给谁绑的自定义事件,就找谁去解绑;
一、解绑自定义事件
1-1、解绑一个自定义事件
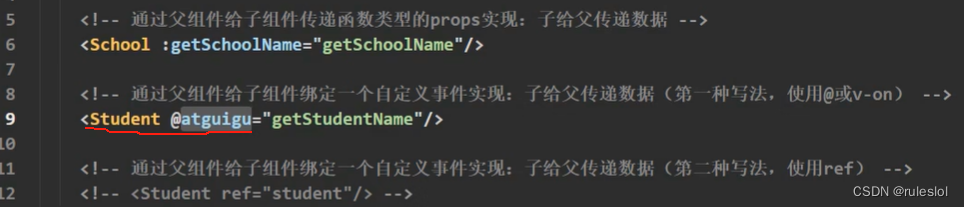
到student.vue组件中去解绑。
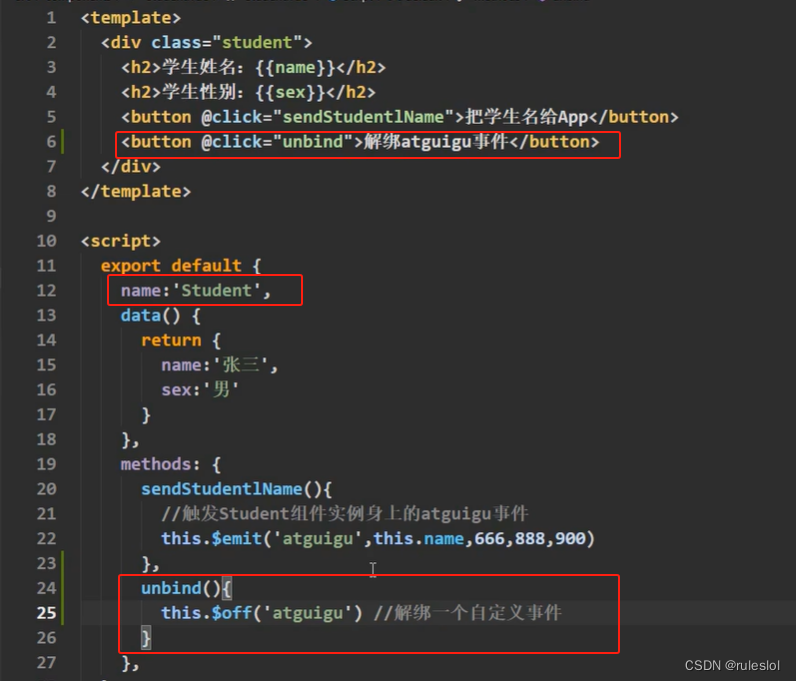
1-2、解绑多个自定义事件

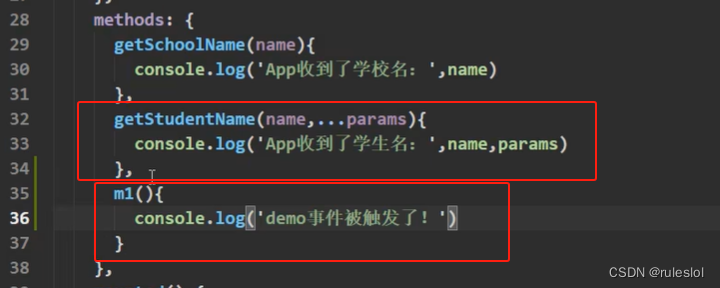
使用数组来解绑多个。

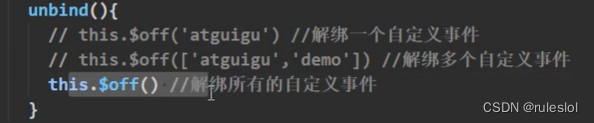
1-3、解绑所有的自定义事件
二、销毁钩子
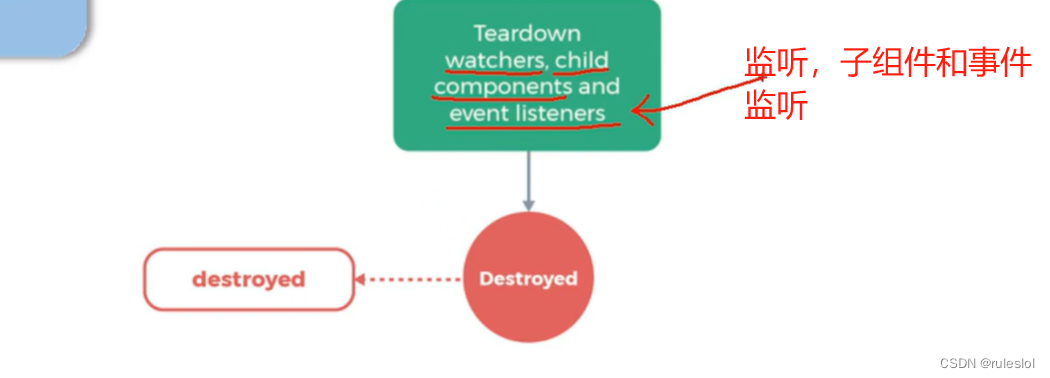
销毁时,移除的事件监听,不是原始的DOM监听,是自定义事件!
2-1、销毁vc

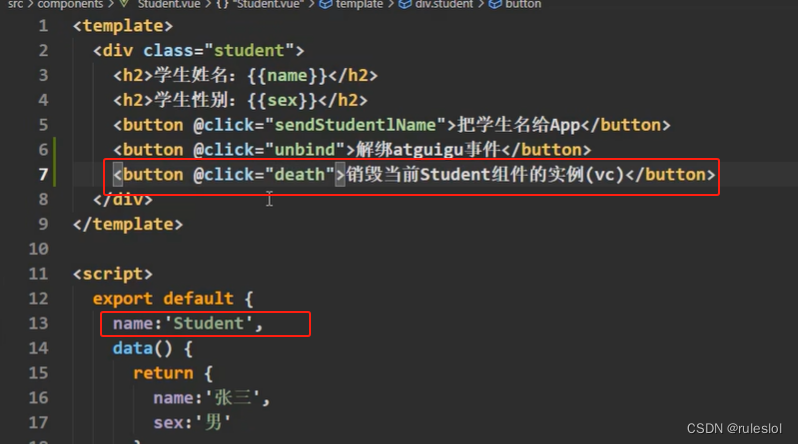
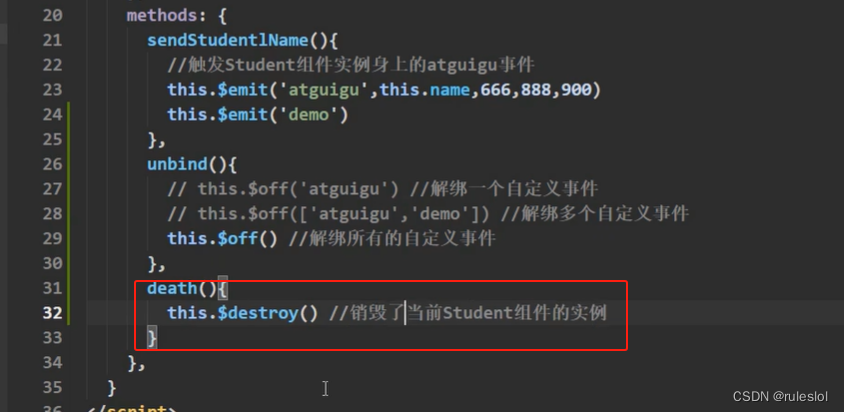
销毁后,所有student实例的自定义事件都不奏效了,但是原生的事件,比如:onclick依然奏效。

因为事件是绑定在VC身上的,VC被销毁了。
2-2、销毁vm

vm都没有了,所有子组件走会被销毁,所有子组件的自定义事件也会被销毁。但是,原生的事件依旧不受影响!
备注:
现在讲的销毁是自杀,亲自去销毁;后面说到路由的时候,就是他杀了,切换页面,组件销毁。
相关文章:

Vue57-组件的自定义事件_解绑
给谁绑的自定义事件,就找谁去触发;给谁绑的自定义事件,就找谁去解绑; 一、解绑自定义事件 1-1、解绑一个自定义事件 到student.vue组件中去解绑。 1-2、解绑多个自定义事件 使用数组来解绑多个。 1-3、解绑所有的自定义事件 二、…...
Java启动jar设置内存分配详解
在微服务架构越来越盛行的情况下,我们通常一个系统都会拆成很多个小的服务,但是最终部署的时候又因为没有那么多服务器只能把多个服务部署在同一台服务器上,这个时候问题就来了,服务器内存不够,这个时候我们就需要对每…...

Feign Client超时时间设置不生效问题
在使用Feign Client时,可以通过两种方式来设置超时时间: 针对整个Feign Client设置超时时间 可以在Feign Client的配置类中通过修改Request.Options对象来设置超时时间。Request.Options对象有两个属性,connectTimeoutMillis用于设置连接超…...

Haproxy部署Web群集
概论 HAProxy是可提供高可用性、负载均衡以及基于TCP和HTTP应用的代理,是免费、快速并且可靠的一种解决方案。HAProxy非常适用于并发大(并发达1w以上)web站点,这些站点通常又需要会话保持或七层处理。HAProxy的运行模式使得它可以…...
C++STL梳理
CSTL标准手册: https://cplusplus.com/reference/stl/ https://cplusplus.com/reference/vector/vector/at/ 1、STL基础 1.1、STL基本组成(6大组件13个头文件) 通常认为,STL 是由容器、算法、迭代器、函数对象、适配器、内存分配器这 6 部分构成&…...

找出1000以内的所有的完数
完数的概念:完数(Perfect Number)是一个正整数,它等于除了它本身以外所有正因子之和。例如,6的因子有1、2、3和6,其中1236,所以6是一个完数。 #include <stdio.h> // 函数用于计算一个数…...

3110. 字符串的分数
给你一个字符串 s 。一个字符串的 分数 定义为相邻字符 ASCII 码差值绝对值的和。 请你返回 s 的 分数 。 示例 1: 输入:s "hello" 输出:13 解释: s 中字符的 ASCII 码分别为:h 104 ,e 1…...

Mybatis MySQL allowMultiQueries 一次性执行多条语句
在JDBC 增加参数allowMultiQueries jdbc:mysql://localhost:3306/abc?&allowMultiQueriestrue <insert id"addRi" parameterType"java.util.List">DELETE FROM sys_ri WHERE sr_id #{roId} AND sr_fion_id #{fod};INSERT into sys_rVALUES&…...

Kubernates容器化JVM调优笔记(内存篇)
Kubernates容器化JVM调优笔记(内存篇) 先说结论背景思路方案 先说结论 1、首先如果是JDK8,需要使用JDK8_191版本以上,才支持容器化环境和以下参数,否则就更新到JDK10以上,选择对应的镜像构建就行了 2、在容…...

Elasticsearch Scroll 报错entity content is too long
2024-06-24 15:22:01:568 ERROR [task-31] (ScrollFetcherProduceAction.java:129) 访问ES出错org.apache.http.ContentTooLongException: entity content is too long [112750110] for the configured buffer limit [104857600]at org.elasticsearch.client.HeapBufferedAsync…...

Vue iview输入框change事件replace正则替换不生效问题的解决。
// 需求:输入座机号只允许输入数字和"-" onChange(e){this.$nextTick(()>{this.phone e.target.value.replace(/[^0-9-]/g, );}) } 解决:添加**this.$nextTick**即可...

Prestashop跨境电商独立站,外贸B2C网站完整教程
Prestashop是一款来自法国专业的开源电商CMS(内容管理系统)平台,和wordpress一样比较轻量,适合中小网站。Prestashop跨境电商独立站在国内并不是很流行,不过国外是非常火的,从各大平台的Prestashop主题数量就可以看得出来。 最有…...

常用算法及参考算法 (1)累加 (2)累乘 (3)素数 (4)最大公约数 (5)最值问题 (6)迭代法
常用算法及参考算法 (1)累加 (2)累乘 (3)素数 (4)最大公约数 (5)最值问题 (6)迭代法 1. 累加 #include <stdio.h>int main() {…...
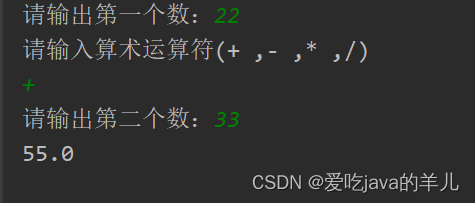
java简易计算器(多种方法)
parseDouble() 方法属于 java.lang.Double 类。它接收一个字符串参数,其中包含要转换的数字表示。如果字符串表示一个有效的 double,它将返回一个 double 值。 应用场景 parseDouble() 方法在以下场景中非常有用: 从用户输入中获取数字&a…...

spring的bean定义和扫描规则
1、bean的基本定义 在Spring框架中,Bean是一个核心概念,它是Spring IoC(Inverse of Control,控制反转)容器管理的一个对象实例。简单来说,Bean就是由Spring容器初始化、配置和管理的对象。这些对象可以是J…...
软件工程体系概念
软件工程 软件工程是应用计算机科学、数学及 管理科学等原理开发软件的工程。它借鉴 传统工程的原则、方法,以提高质量,降 低成本为目的。 一、软件生命周期 二、软件开发模型 1.传统模型 瀑布模型、V模型、W模型、X 模型、H 模型 (1)瀑布模型 瀑布…...
史上最全整合nacos单机模式整合哈哈哈哈哈
Nacos 是阿里巴巴推出的一个新开源项目,它主要是一个更易于构建云原生应用的动态服务发现、配置管理和服务管理平台。 Nacos提供了一组简单易用的特性集,帮助用户快速实现动态服务发现、服务配置、服务元数据及流量管理。 Nacos 的关键特性包括&#x…...

Python xml.dom.minidom 读取XML元素
哈喽,大家好,我是木头左! 什么是 XML? XML(可扩展标记语言)是一种用于描述数据结构和交换数据的标记语言。它被广泛用于 Web 应用程序中,用于存储和传输数据。XML 具有自描述性,因此可以很容易地理解和处理。 Python 中的 xml.dom.minidom Python 提供了一个内置的库…...

【Python/Pytorch 】-- K-means聚类算法
文章目录 文章目录 00 写在前面01 基于Python版本的K-means代码02 X-means方法03 最小二乘法简单理解04 贝叶斯信息准则 00 写在前面 时间演变聚类算法:将时间演变聚类算法用在去噪上,基本思想是,具有相似信号演化的体素具有相似的模型参数…...

【Eureka】介绍与基本使用
Eureka介绍与基本使用 一个简单的Eureka服务器的设置方法:1 在pom.xml中添加Eureka服务器依赖:2 在application.properties或application.yml中添加Eureka服务器配置:3 创建启动类,使用EnableEurekaServer注解启用Eureka服务器&am…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
