【Python/Pytorch 】-- K-means聚类算法

文章目录
文章目录
- 00 写在前面
- 01 基于Python版本的K-means代码
- 02 X-means方法
- 03 最小二乘法简单理解
- 04 贝叶斯信息准则
00 写在前面
时间演变聚类算法:将时间演变聚类算法用在去噪上,基本思想是,具有相似信号演化的体素具有相似的模型参数值,并且由机器学习决定的集群数量远远小于体素的数量。因此,对一个聚类进行平均可以大大提高聚类级逆解的信噪比,这可以用作体素级优化的鲁棒初始猜测。
在该演变算法的基础上,总结了K-means算法、X-means算法、最小二乘法、贝叶斯信息准则
01 基于Python版本的K-means代码
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs# 生成具有三个簇的示例数据
n_samples = 300
n_features = 2
centers = 3
cluster_std = 1.0x, y = make_blobs(n_samples=n_samples, n_features=n_features, centers=centers, cluster_std=cluster_std, random_state=42)# 设置K值(簇的数量)
k = 3# 初始化KMeans算法
kmeans = KMeans(n_clusters=k, random_state=42)# 进行聚类
kmeans.fit(X)# 获取聚类结果
labels = kmeans.labels_
centroids = kmeans.cluster_centers_# 绘制聚类结果
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', marker='o', edgecolor='k', s=50)
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='x', s=200, linewidths=3, zorder=10)
plt.title('K-means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid(True)
plt.show()
02 X-means方法
传统的K-means聚类算法需要预先确定聚类的数量K。在这里,使用了一种称为X-means的方法,该方法能够自动选择K。X-means方法通过两个步骤反复迭代来选择合适的聚类数量K。
- 步骤1:
- 首先执行传统的K-means聚类,给定一个初始的聚类数量。
- 计算贝叶斯信息准则(BIC),BIC是聚类对数似然和对K的惩罚项的和。
- 随着K的增加,拟合的优度(对数似然)增加,但过拟合的可能性也增加。惩罚项用来减少这种可能性。
- 步骤2:
- 每个聚类的质心(质心)被替换为两个子质心,并在该聚类内使用这些子质心作为初始猜测进行局部K-means(K = 2)。
- 计算该聚类的BIC:如果BIC较大,则进行替换,否则保留“父”质心。
- 重复步骤1和步骤2,直到整体BIC不再增加或 K达到预先设定的最大值为止。
- 在这项研究中,初始聚类数为1,最大聚类数为50。
03 最小二乘法简单理解
最小二乘法(Least Squares Method, LSM)是统计学和数据分析中常用的一种方法,用于拟合数据模型。它的本质是一个优化过程,因为它通过最小化目标函数来找到模型参数的最优解。
(1)最小二乘法的基本思想
假设我们有一组观测数据点(x1, y1),(x2, y2),…,(xn, yn),我们希望找到一个函数 f(x)来拟合这些数据点。最简单的情况是线性拟合,即找到一个直线模型 y=ax+b,使得该直线尽可能靠近所有观测数据点。
最小二乘法的目标是最小化以下目标函数(误差的平方和):
S ( a , b ) = ∑ i = 1 n ( y i − ( a x i + b ) ) 2 S(a,b) = {\textstyle \sum_{i=1}^{n}} (y_{i}-(ax_{i}+b) )^{2} S(a,b)=∑i=1n(yi−(axi+b))2
其中,yi是观测值,axi+b是预测值。
(2)最小二乘法的优化过程
- 步骤1:
定义目标函数:目标函数S(a,b) 表示预测值与观测值之间的误差的平方和。 - 步骤2:
求导数:为了找到使目标函数最小的参数 a 和b,我们对 S(a, b) 分别对a 和 b 求偏导数,并将其设为零,得到一组方程:
∂ S ∂ a = − 2 ∑ i = 1 n x i ( y i − a x i − b ) = 0 \frac{\partial S}{\partial a} = -2 {\textstyle \sum_{i=1}^{n}} x_{i}(y_{i}-ax_{i}-b)=0 ∂a∂S=−2∑i=1nxi(yi−axi−b)=0
∂ S ∂ b = − 2 ∑ i = 1 n ( y i − a x i − b ) = 0 \frac{\partial S}{\partial b} = -2 {\textstyle \sum_{i=1}^{n}} (y_{i}-ax_{i}-b)=0 ∂b∂S=−2∑i=1n(yi−axi−b)=0 - 步骤3:
解方程:通过求解上述方程组,可以得到最优参数 a 和 b 的值。具体求解过程可以得到如下结果:
a = n ∑ i = 1 n x i y i − ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n x i 2 − ( ∑ i = 1 n x i ) 2 a = \frac{n {\textstyle \sum_{i=1}^{n}}x_{i}y_{i}-\sum_{i=1}^{n}x_{i}\sum_{i=1}^{n}y_{i} }{n {\textstyle \sum_{i=1}^{n}}x_{i}^{2}-({\textstyle \sum_{i=1}^{n}}x_{i})^{2} } a=n∑i=1nxi2−(∑i=1nxi)2n∑i=1nxiyi−∑i=1nxi∑i=1nyi
b = ∑ i = 1 n y i − a ∑ i = 1 n x i n b = \frac{{\textstyle \sum_{i=1}^{n}}y_{i}-a\sum_{i=1}^{n}x_{i}}{n} b=n∑i=1nyi−a∑i=1nxi - 步骤4:
优化的本质:最小二乘法的过程实际上是通过优化方法来最小化目标函数。优化在这里的意思是找到使目标函数达到最小值的参数组合。在最小二乘法中,这个目标函数是误差的平方和,优化过程就是通过求解导数来找到误差平方和的最小值。
04 贝叶斯信息准则
贝叶斯信息准则(Bayesian Information Criterion, BIC)是一种统计量,用于模型选择,特别是在评估模型复杂性和拟合优度之间的平衡时使用。
BIC 的计算公式如下:
B I C = − 2 l n ( L ) + k l n ( n ) BIC=-2ln(L) +kln(n) BIC=−2ln(L)+kln(n)
其中:
- ln(L)是模型的对数似然(log-likelihood)。对数似然度量了模型对数据的拟合优度。对数似然值越大,说明模型越能解释数据。
- k是模型的参数数量。在聚类模型中,参数数量通常包括聚类数K和每个聚类的参数(如均值和方差)。k越大,模型越复杂。
- n是样本数量。样本数量是指数据中的观测值个数。
- BIC 的公式中,-2ln(L)代表了模型的拟合优度,值越小,拟合越好。kln(n)是对模型复杂性的惩罚项,随着参数数量 k 和样本数量n的增加,惩罚项也增加。这个项用来防止过拟合。BIC 的值越小,模型越好。因此,在选择模型时,希望找到使 BIC 最小的模型。
相关文章:

【Python/Pytorch 】-- K-means聚类算法
文章目录 文章目录 00 写在前面01 基于Python版本的K-means代码02 X-means方法03 最小二乘法简单理解04 贝叶斯信息准则 00 写在前面 时间演变聚类算法:将时间演变聚类算法用在去噪上,基本思想是,具有相似信号演化的体素具有相似的模型参数…...

【Eureka】介绍与基本使用
Eureka介绍与基本使用 一个简单的Eureka服务器的设置方法:1 在pom.xml中添加Eureka服务器依赖:2 在application.properties或application.yml中添加Eureka服务器配置:3 创建启动类,使用EnableEurekaServer注解启用Eureka服务器&am…...
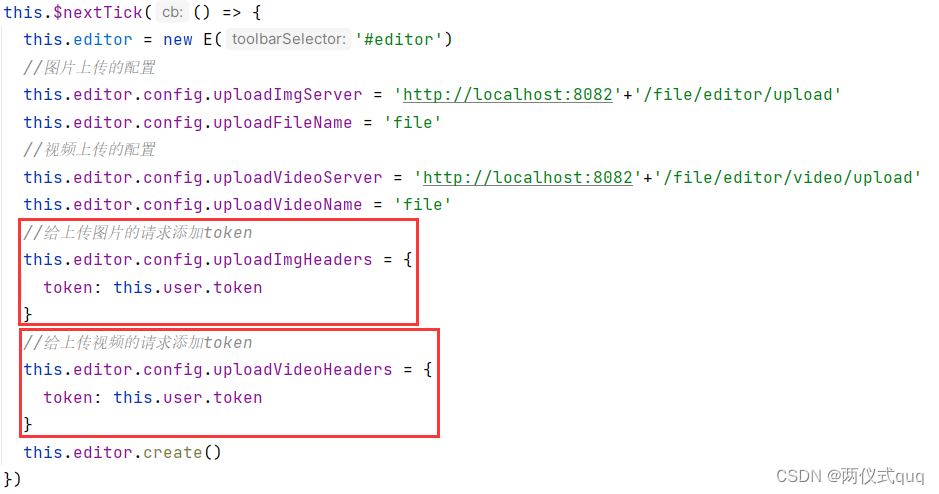
SpringBoot+Vue集成富文本编辑器
1.引入 我们常常在各种网页软件中编写文档的时候,常常会有富文本编辑器,就比如csdn写博客的这个页面,包含了富文本编辑器,那么怎么实现呢?下面来详细的介绍! 2.安装wangeditor插件 在Vue工程中,…...

React@16.x(34)动画(中)
目录 3,SwitchTransition3.1,原理3.1.2,key3.1.2,mode 3.2,举例3.3,结合 animate.css 4,TransitionGroup4.1,其他属性4.1.2,appear4.1.2,component4.1.3&…...

ONLYOFFICE 8.1:全面升级,PDF编辑与本地化加强版
目录 📘 前言 📟 一、什么是 ONLYOFFICE 桌面编辑器? 📟 二、ONLYOFFICE 8.1版本新增了那些特别的实用模块? 2.1. 轻松编辑器 PDF 文件 2.2. 用幻灯片版式快速修改幻灯片 2.3. 无缝切换文档编辑、审阅和查…...

C++ 入门
前言 c的发展史: C的起源可以追溯到1979年,当时Bjarne Stroustrup在贝尔实验室开始开发一种名为“C with Classes”的语言。以下是C发展的几个关键阶段: 1979年:Bjarne Stroustrup在贝尔实验室开始开发“C with Classes”。1983…...

GPT-5发布倒计时:AI智能从高中生到博士生的跨越
嘿,小伙伴们!最近有个大新闻,OpenAI的首席技术官米拉穆拉蒂在一次采访中透露,GPT-5将在一年半后发布。她把这个升级比作从聪明的高中生到博学的博士生的飞跃,听起来是不是很酷? 现在GPT-4o还有不少功能没上…...

Docker 拉取镜像失败处理 配置使用代理拉取
解决方案 1、在 /etc/systemd/system/docker.service.d/http-proxy.conf 配置文件中添加代理信息 2、重启docker服务 具体操作如下: 创建 dockerd 相关的 systemd 目录,这个目录下的配置将覆盖 dockerd 的默认配置 代码语言:javascript 复…...

视频汇聚安防综合管理系统EasyCVR平台GB28181设备注册未上线的原因排查与解决
视频汇聚安防综合管理平台EasyCVR视频监控系统基于云边端架构,可支持海量视频汇聚集中管理,能提供视频监控直播、云端录像、云存储、录像检索与回看、告警(协议告警/智能告警/1400视图库告警)、平台级联、AI智能分析接入等视频能力…...
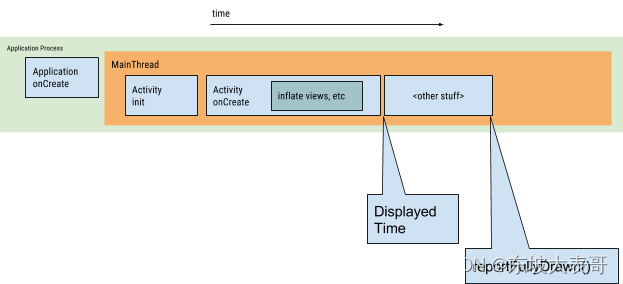
【性能优化】Android冷启动优化
文章目录 常见现象APP的启动流程计算启动时间Displayed Timeadb dump 启动优化具体策略总结参考链接 常见现象 各种第三方工具初始化和大量业务逻辑初始化,影响启动时间,导致应用启动延迟、卡顿等现象 APP的启动流程 加载和启动应用程序; …...

Git拉完整代码缺少某个类
已找到具体问题,对比之后发现应该是拉去的文件名字字符太长导致! 使用 Git LFS Git LFS(Large File Storage)是 Git 的一个扩展,它可以帮助管理大型文件,包括长文件名。如果你的项目包含大量的大型文件或长…...
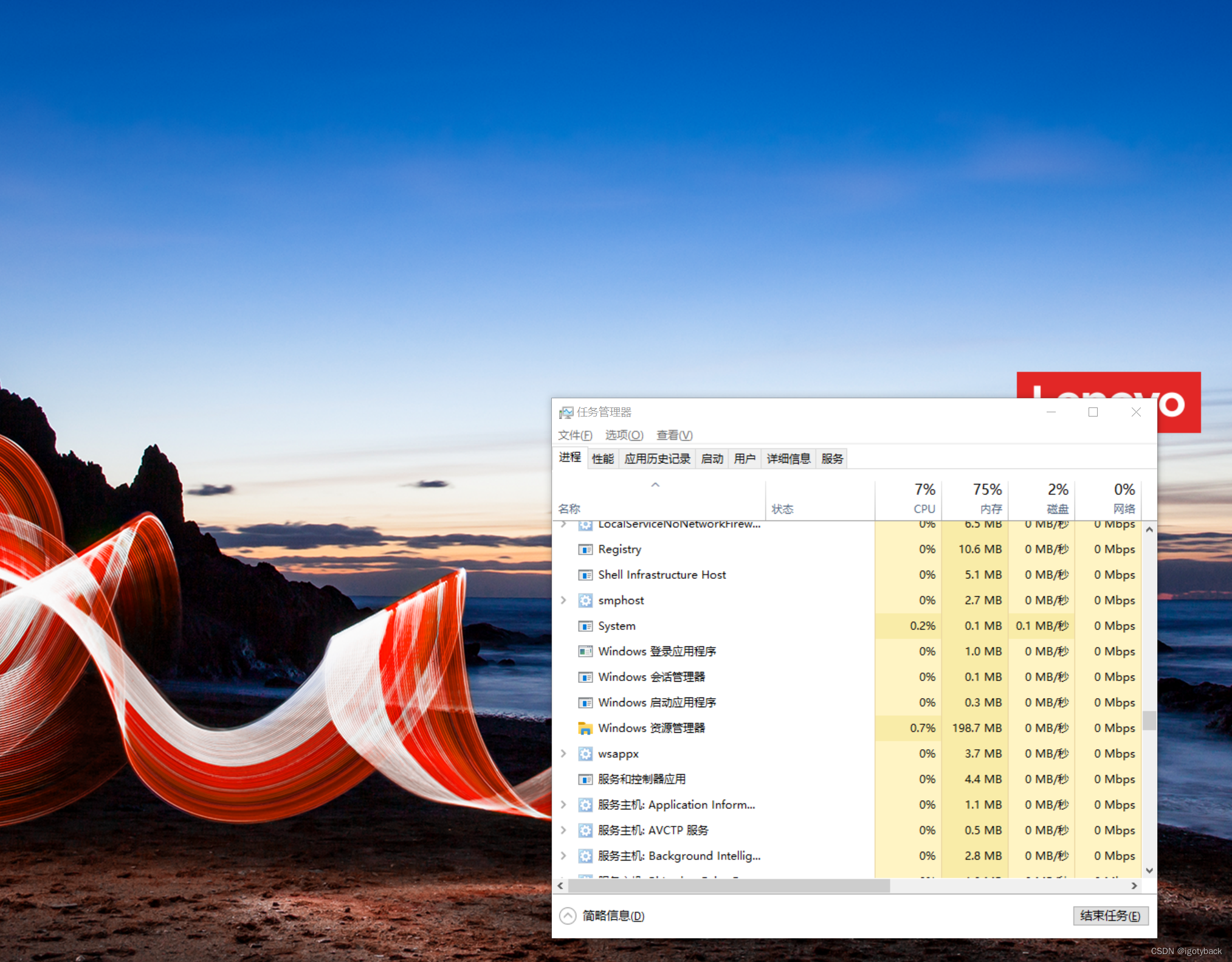
Windows资源管理器down了,怎么解
ctrlshiftesc 打开任务管理器 文件 运行新任务 输入 Explorer.exe 资源管理器重启 问题解决 桌面也回来了...
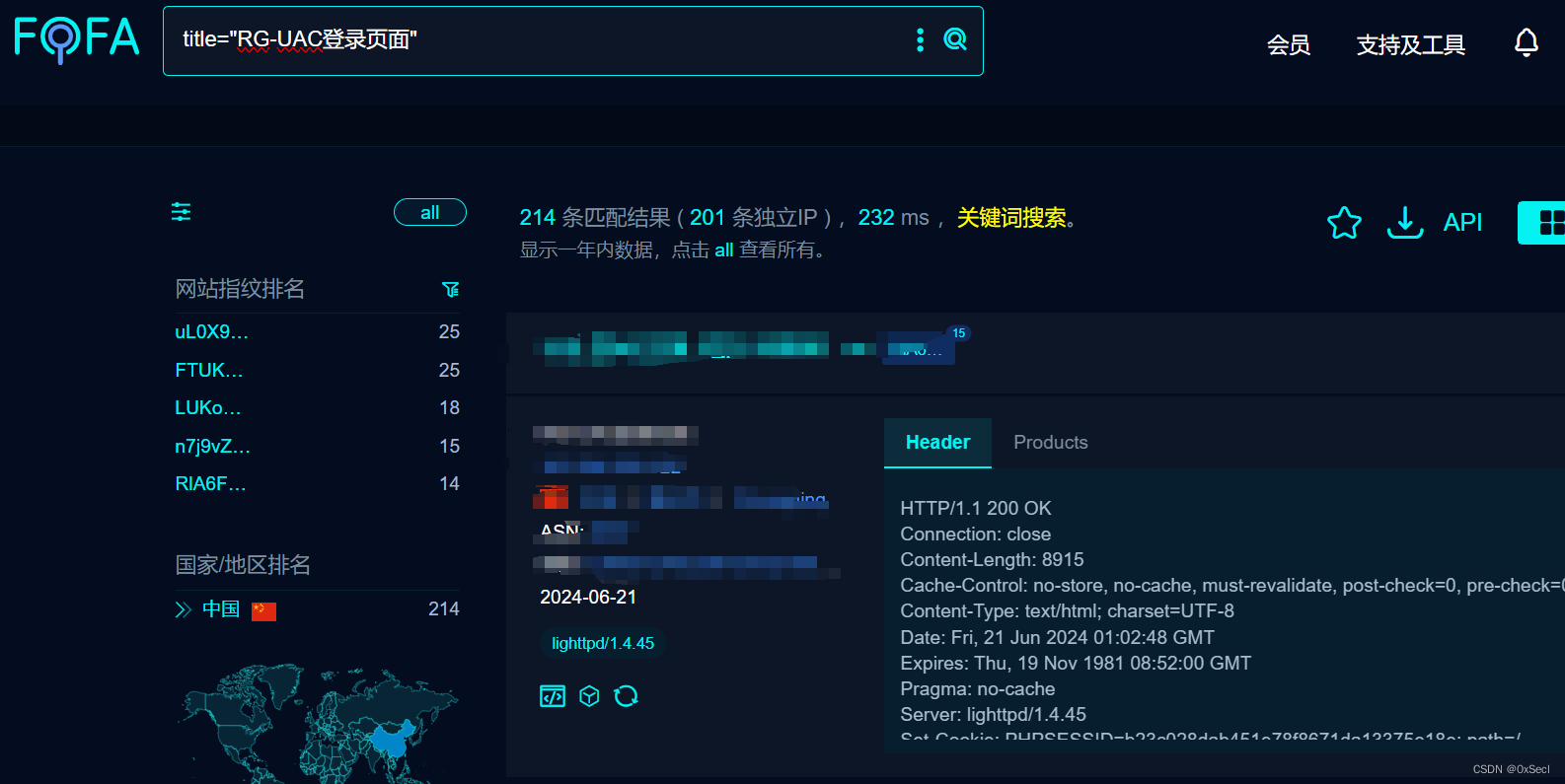
锐捷统一上网行为管理与审计系统 static_convert.php 前台RCE漏洞复现
0x01 产品简介 锐捷统一上网行为管理与审计RG-UAC系列是星网锐捷网络有限公司自主研发的上网行为管理与审计产品,具备的上网行为日志审计功能,能够全面、准确、细致的审计并记录多种上网行为日志,包括网页、搜索、外发文件、邮件、论坛、IM等等,并对日志数据进行统计分析,…...

在Linux/Ubuntu/Debian中使用SSH连接远程服务器VPS
在Linux/Ubuntu/Debian中使用SSH连接远程服务器VPS 在远程管理服务器时,SSH(Secure Shell)协议是我们常用的工具之一。它提供了一种加密的方式来访问和管理远程主机。默认情况下,SSH使用22端口,但有时我们需要通过指定…...

如何安全进行亚马逊、沃尔玛测评?
在亚马逊、沃尔玛、速卖通、阿里国际站等电商平台上,测评已成为一种高效的推广手段,但伴随的风险也不容忽视。这些风险主要源于平台严格的大数据风控机制,它涵盖了多个方面,以确保评价的真实性和合规性。 首先,硬件参数…...

自动化喷涂生产线控制方法概述
喷涂生产线涉及控制机械臂及传送带等,以及触摸屏人机界面,以及各种电机,电磁阀等,本文针对具体控制方法进行讨论。 一套自动化喷涂生产线装配完成后,进入到控制调试阶段,首先要进行工艺参数的设置ÿ…...
【Linux】Centos升级到国产操作系统Openeuler
一、前言 迁移工具采用Openeuler官网提供的x2openEuler工具,是一款将源操作系统迁移到目标操作系统的迁移工具套件,具有批量化原地升级能力,当前支持将源 OS 升级至 openEuler 20.03。 官网链接:openEuler迁移专区 | 迁移专区首页…...

【扫雷游戏】C语言详解
Hi~!这里是奋斗的小羊,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~ 💥💥个人主页:奋斗的小羊 💥💥所属专栏:C语言 🚀本系列文章为个人学习…...

自定义平台后台登录地址前缀的教程
修改平台后台地址默认的 admin 前缀 修改后端 config/admin.php 配置文件,为自定义的后缀修改 平台后台前端源码中 src/settings.js 文件,修改为和上面一样的配置修改后重新打包前端代码,并且覆盖到后端的 public 目录下重启 swoole 服务即可...

kylin v10 离线安装chrome centos离线安装chrome linux离线安装谷歌浏览器
1. 先用自己联网的计算机,下载离线安装包,浏览器输入链接下载安装包: https://dl.google.com/linux/direct/google-chrome-stable_current_x86_64.rpm 1.2. 信创环境不用执行下面,因为没网 1.3. 若为阿里云服务器,或服…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
