【C++】红黑树
文章目录
- 红黑树的概念
- 红黑树的性质特征
- 红黑树结点的定义
- 红黑树的插入操作
- 情况1
- 情况2
- 情况3
- 特殊情况
- 代码实现
- 红黑树的验证
- 红黑树的删除
- 红黑树和AVL树的比较
- 红黑树的应用
红黑树的概念
红黑树,是一种二叉搜索树,但是每一个结点都增加一个存储位表示结点的颜色,可以是red或者black。通过任何一条从根到叶子结点的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出两倍,因而是接近平衡的。
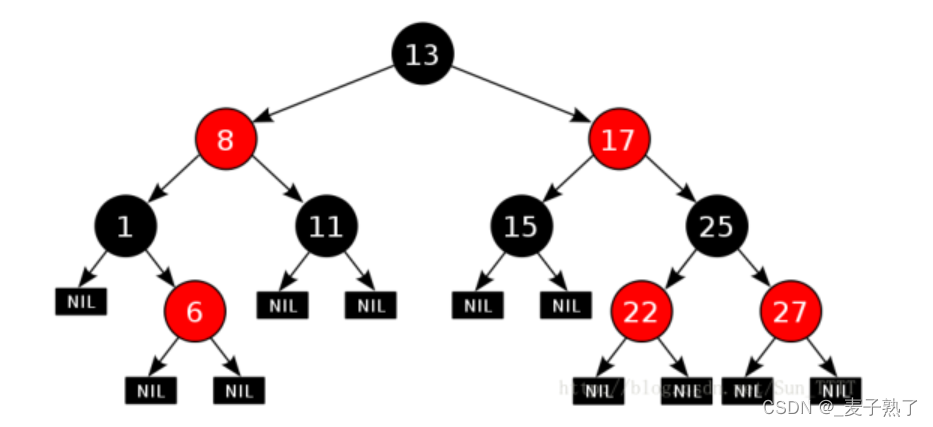
红黑树的性质特征
- 每个结点不是黑色就是红色;
- 根节点_root是黑色;
- 如果一个结点是红色的,则它的两个孩子结点是黑色的(即没有连续的红色结点,注意可以有连续的黑色结点);
- 对于每个结点,从该结点到其所有后代叶子的简单路径上,均包含相同数目的黑色结点(即每条路径上都包含相同数量黑色结点);
- 空节点,即NIL结点可以认为是黑色的,注意:计算有几条路径时,是要看是否走到空节点,即图上的NIL空节点,故如图的红黑树有5条路径;
思考:为什么满足上面的性质,红黑树就能保证其最长路径中结点个数不会超过最短路径结点个数的两倍?
红黑树是近似平衡,不能保证每次都完全平衡。由性质3可知红色结点不能连续,由性质4可得每条路径均包含相同数量的黑色结点。
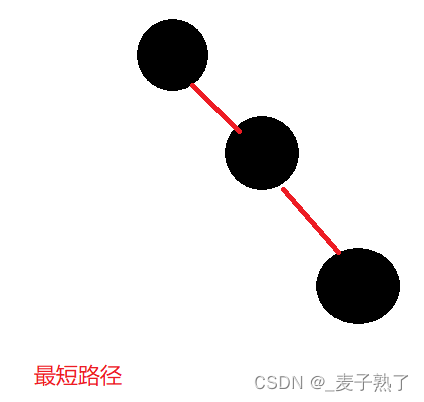
若我们假设从根到叶子结点的路径中包含黑色结点的数量为N。
最短路径:全黑,长度为N,高度logN
最长路径:一黑一红相间,记住要保证每条路径包含的黑色结点个数是相同的,那么长度为2N,高度2logN
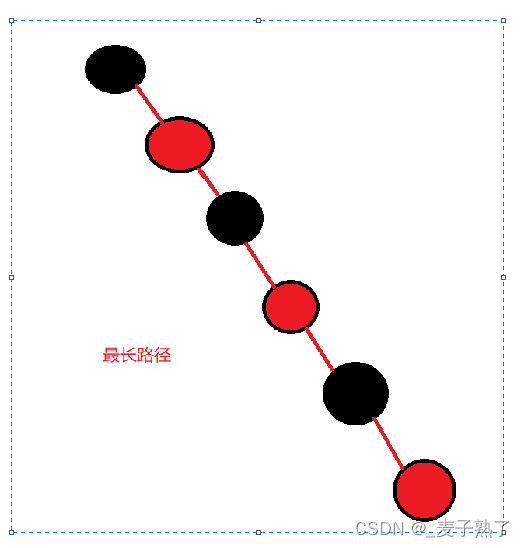
最优情况:
如果需要保证左右平衡,那么有可能是全黑 或者 每条路径都是一黑一红相间的路径(满二叉树)。
最差情况:
左子树全黑,右子树一黑一红
可以发现,最坏情况的时间复杂度和AVL树(严格平衡)一样,都是O(logN),但是红黑树(“非严格平衡”)这种近似平衡的结构减少了大量旋转,综合性能优于AVL树。
红黑树结点的定义
红黑树的实现类似AVL树,我们采用KV模型实现红黑树,并采用三叉链结构,除此之外,我们需要引入一个新的成员变量表示:结点的颜色。这里我们采用枚举的方式定义结点颜色,这样可以增加代码的可读性和可维护性,便于后序操作。
//利用枚举定义颜色
enum colour
{RED,//0BLACK//1
};
//红黑树结点的定义
template <class K,class V>
struct RBTreeNode
{//<key,value>pair<K, V> _kv;//三叉链结构RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;//结点的颜色int _col;//构造函数RBTreeNode<K, V>(const pair<K, V>& kv): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){ }
};
为什么构造结点的时候,结点的颜色默认设置成红色?
我们先来回顾一下红黑树的性质3和性质4:没有连续的红色结点;每条路径上包含相同数量的黑色结点。
当我们向红黑树插入结点时,若插入的是黑色结点,那么所插入的那条路径上就比其他路径多了一个黑色结点,这必然破换了性质4,此时我们就需要对红黑树进行调整。
当我们向红黑树插入的是红色结点时,如果此时插入结点的父节点也是红色结点,那么就出现了连续的红色结点,这就会破坏性质3,此时我们需要对红黑树进行调整。如果父节点是黑色的,我们就不需要对红黑树进行调整。
即插入黑色结点,一定破坏红黑树的性质4,必须对红黑树进行调整。插入红色结点,可能会破坏红黑树的性质3,可能需要对红黑树进行调整。综合看来,插入红色结点更好。
红黑树的插入操作
红黑树一开始的插入操作跟AVL树一样,关键在于第三步。
- 如果根节点为空,先创建一个根节点(注意红黑树根节点是黑色的)
- 找到插入结点插入的位置
- 如果插入结点的父节点是红色的,则需要对红黑树进行调整
红黑树在插入结点后,如何对红黑树进行调整?
如果插入结点的父节点是黑色的,则不需要对红黑树进行调整。(不破坏红黑树的性质)。
如果插入结点的父节点是红色的,则需要对红黑树进行调整,因为我们默认插入的结点颜色是红色的,这样就会出现连续的红色结点。
下面具体将红黑树的调整分成3种情况,重点关注插入结点的父节点,叔叔结点(即父节点的兄弟结点),祖父结点。
情况1
注意以下看到的树,可能是一棵完整的树,也可能是一棵子树,以下是抽象图的展示。
插入结点的父节点是红色,祖父结点是黑色,叔叔存在,且结点是红色。
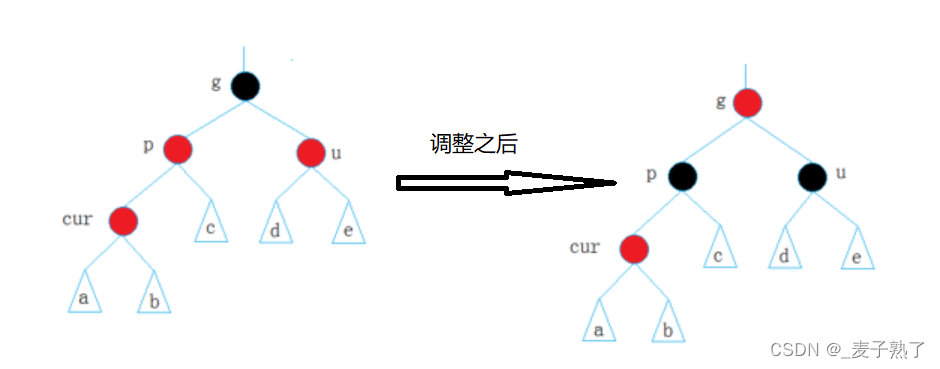
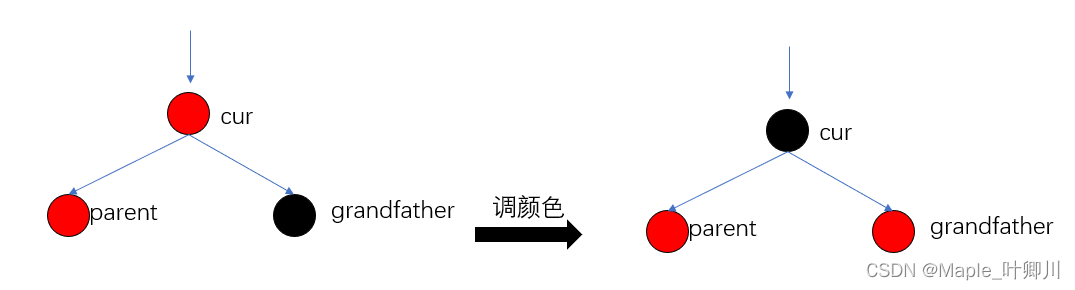
调整方式:我们先观察调整之前的图形,这种情况下,插入新的结点之后,会出现连续的红色结点,并且从g开始,每条路径包含的黑色结点的数量为1。
那么为了避免出现连续的红色结点,我们可以将父节点变黑,但是为了保持每条路径黑色结点的数目不变,因此我们还需要把祖父结点变红,再将叔叔结点变黑,这样就可以保持每条路径的黑色结点数目是相同的了,也解决了红色结点连续的问题。
相信同学们还有疑问,不是说根节点必须是黑色的吗,为什么颜色调整之后,根变成了红色呢?
不要急,因为调整还未结束。这种情况下祖父结点变成了红色,如果祖父结点是根结点,那么我们直接将祖父结点变成黑色即可。此时每条路径的保护的黑色结点又多了一个,调整之前每条路径的黑色结点是1个,现在每条路径包含的黑色结点是两个,依然满足性质4.
但如果祖父结点不是根结点,这棵树是一棵子树,那么我们就需要将祖父结点当作新插入的结点,再判断其父节点是否为红色,若父节点也是红色,那么需要根据叔叔的情况,进行不同的调整。
注意:插入结点的父节点为红,叔叔结点存在且为红时,cur结点无论是parent的左孩子还是右孩子,调整方式都是一样的。
情况2
插入结点的叔叔不存在,即插入结点的父节点的兄弟结点不存在。
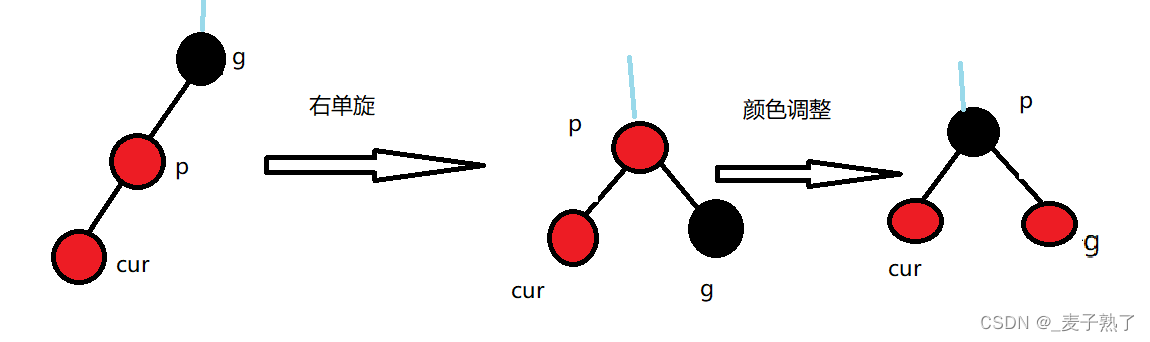
若插入结点的叔叔不存在,那么cur一定是新插入的结点,而不是其它情况向上调整变化而来的,因为叔叔不存在,则p的孩子不可能存在黑色结点(遵循性质4)。
这种情况下,祖孙三代的关系是一条直线,我们需要先进行单旋操作,再进行颜色调整,颜色调整后,这棵子树的根节点变成了黑色,所以不需要再向上继续调整。
若p是g的左孩子,cur是p的左孩子,则这棵子树的左边较高,我们以p为轴点,进行右单旋,再将parent父节点改为黑色,祖父结点改为红色;
若p是g的右孩子,cur是p的左孩子,则这棵子树的右边较高,我们以p为轴点,进行左单旋,再将parent父节点改为黑色,祖父结点改为红色。
情况3
插入结点的叔叔存在。且叔叔结点为黑色。
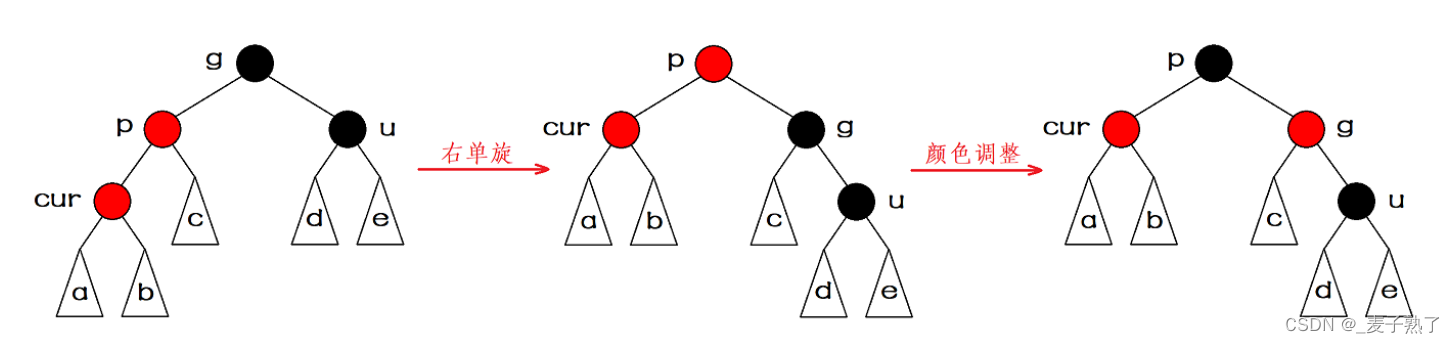
这种情况下一定是上次情况一调整之后出现的,cur不可能是新插入的结点,否则就不遵循性质4,每条路径包含的黑色结点数量相同了。
这时单纯的变色无法直接解决问题,情况三是由情况2变化而来的,所以我们依然需要先进行单旋操作,再进行颜色调整,parent父节点改为黑色,祖父结点u改成红色,叔叔结点u依然保持黑色。颜色调整成功后,这棵子树的根节点是黑色的,所以无需继续向上进行调整。
同理:
若p是g的左孩子,cur是p的左孩子,则这棵子树的左边较高,我们以p为轴点,进行右单旋,再将parent父节点改为黑色,祖父结点改为红色;
若p是g的右孩子,cur是p的左孩子,则这棵子树的右边较高,我们以p为轴点,进行左单旋,再将parent父节点改为黑色,祖父结点改为红色。
注意:情况二和情况三都是先进行旋转操作,再进行颜色调整。并且调整成功后,这棵子树的根节点已经变成黑色,无需再进行向上调整。只有情况一,祖父结点被改成红色,才需要继续向上调整。
特殊情况
前面的情况123,parent,cur,grandparents,都是连成一条直线的。那么这个所谓的特殊情况,就是parent,cur,grandparents的路径从形状上看来,是一条折线。
若形状呈一条折线,那么有以下两种情况:
- parent在grandparents的左边,cur在parent的右边
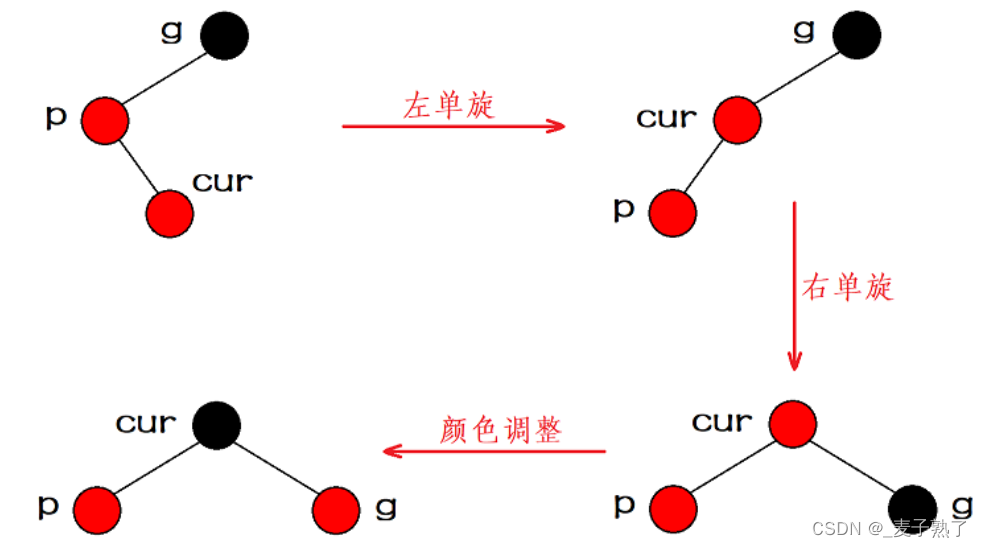
解决方法:以parent为轴点先进行左单旋,再以g为轴点进行右单旋(即左右双旋),最后调整结点颜色,将cur变成黑色,将grandparents变成红色;
- parent在grandparents的右边,cur在parent的左边
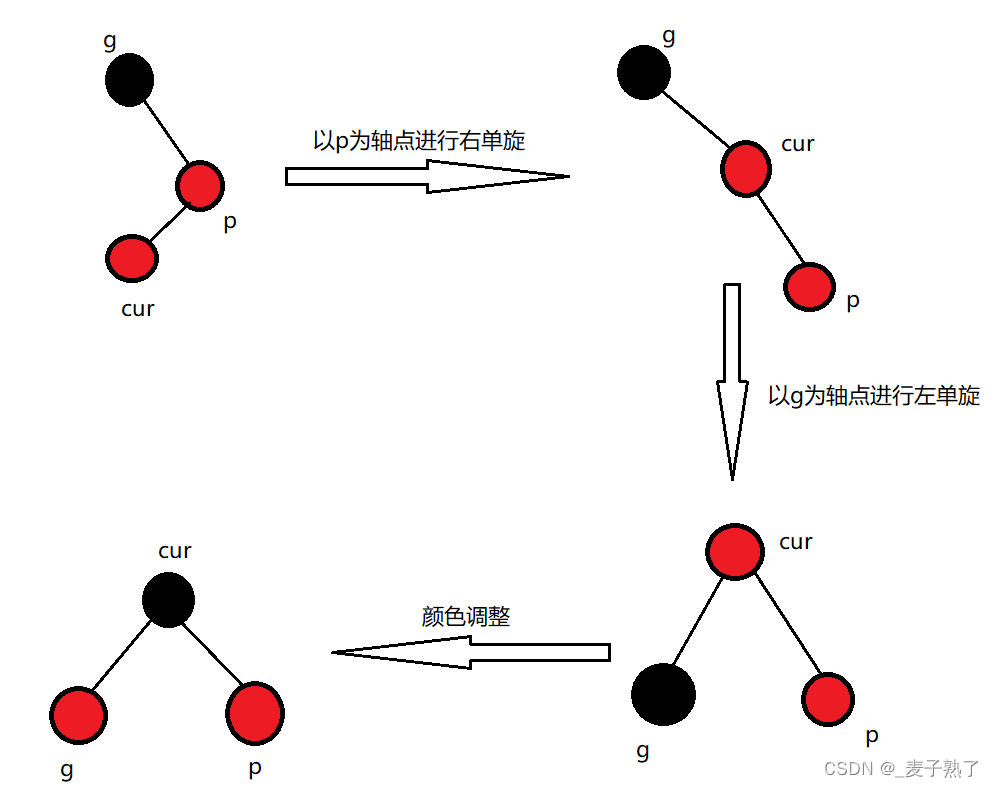
解决方法:先以p为轴点进行右单旋,接着以g为轴点进行左单旋,最后调整结点颜色,将cur结点变成黑色,将g结点变成红色。
注意:除了情况一调整之后g结点会变成红色,需要继续向上调整,其它情况颜色调整完后,g(子树)根节点都会被调整成黑色,因此不需要继续向上调整。
代码实现
bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED){Node* grandfater = parent->_parent;if (parent == grandfater->_left){Node* uncle = grandfater->_right;// 情况一 uncle存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfater->_col = RED;cur = grandfater;parent = cur->_parent;}else{if (cur == parent->_left){// 情况二RotateR(grandfater);parent->_col = BLACK;grandfater->_col = RED;}else{// 情况三RotateL(parent);RotateR(grandfater);cur->_col = BLACK;grandfater->_col = RED;}break;}}else // (parent == grandfater->_right){Node* uncle = grandfater->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfater->_col = RED;cur = grandfater;parent = cur->_parent;}else{// g // p// cif (cur == parent->_right){RotateL(grandfater);parent->_col = BLACK;grandfater->_col = RED;}else{// g // p// cRotateR(parent);RotateL(grandfater);cur->_col = BLACK;grandfater->_col = RED;}break;}}}_root->_col = BLACK;return true;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;//if (_root == parent)if (ppNode == nullptr){_root = subL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}
红黑树的验证
1.验证其是否为二叉搜索树(通过中序遍历)
2.验证其是否满足红黑树的性质,包括根节点为黑,不能出现连续的红色结点,每条路径包含的黑色结点的数量要相同。
//中序遍历判断是否为二叉搜索树void Inorder(){_Inorder(_root);}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}bool Check(Node* root, int blackNum, const int ref){//root为空,意味着走到了空节点if (root == nullptr){//cout << blackNum << endl;if (blackNum != ref){cout << "违反规则:本条路径的黑色节点的数量跟最左路径不相等" << endl;return false;}return true;}//出现连续的红色结点,则直接返回falseif (root->_col == RED && root->_parent->_col == RED){cout << "违反规则:出现连续红色节点" << endl;return false;}//统计路径中黑色结点的数量if (root->_col == BLACK){++blackNum;}return Check(root->_left, blackNum, ref)&& Check(root->_right, blackNum, ref);}bool IsBalance(){//空树也是平衡二叉树if (_root == nullptr){return true;}//如果根节点不是黑色,则直接返回falseif (_root->_col != BLACK){return false;}//ref是reference的缩写,翻译为参考//记录最左边黑色结点的数量int ref = 0;//以最左边的路径包含的黑色结点数量为参考值,进行各路径的比对Node* left = _root;while (left){if (left->_col == BLACK){++ref;}left = left->_left;}//利用check函数进行各条路径的比对return Check(_root, 0, ref);}
红黑树的删除
红黑树的删除本节不做讲解,有兴趣的同学可参考:《算法导论》或者《STL源码剖析》
链接
红黑树和AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O(log2Nlog_2 Nlog2N),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
红黑树的应用
- C++ STL库 – map/set、mutil_map/mutil_set
- Java 库
- linux内核
- 其他一些库
相关文章:

【C++】红黑树
文章目录红黑树的概念红黑树的性质特征红黑树结点的定义红黑树的插入操作情况1情况2情况3特殊情况代码实现红黑树的验证红黑树的删除红黑树和AVL树的比较红黑树的应用红黑树的概念 红黑树,是一种二叉搜索树,但是每一个结点都增加一个存储位表示结点的颜…...
【剧前爆米花--爪哇岛寻宝】进程的调度以及并发和并行,以及PCB中属性的详解。
作者:困了电视剧 专栏:《JavaEE初阶》 文章分布:这是关于进程调度、并发并行以及相关属性详解的文章,我会在之后文章中更新有关线程的相关知识,并将其与进程进行对比,希望对你有所帮助。 目录 什么是进程/…...
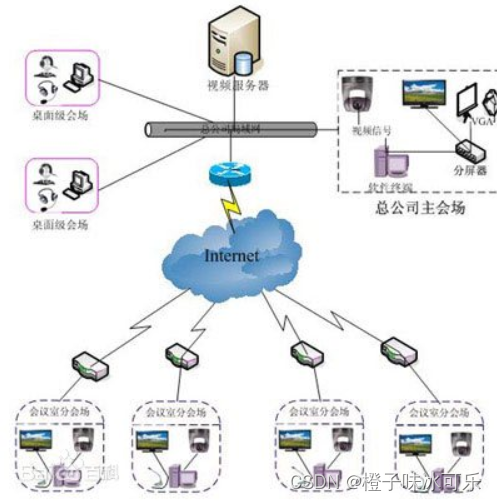
网络的瓶颈效应
python从小白到总裁完整教程目录:https://blog.csdn.net/weixin_67859959/article/details/129328397?spm1001.2014.3001.5501 ❤ 网络的瓶颈效应 网络瓶颈,指的是影响网络传输性能及稳定性的一些相关因素,如网络拓扑结构,网线࿰…...
【C++进阶】四、红黑树(三)
目录 一、红黑树的概念 二、红黑树的性质 三、红黑树节点的定义 四、红黑树的插入 五、红黑树的验证 六、红黑树与AVL树的比较 七、完整代码 一、红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可…...
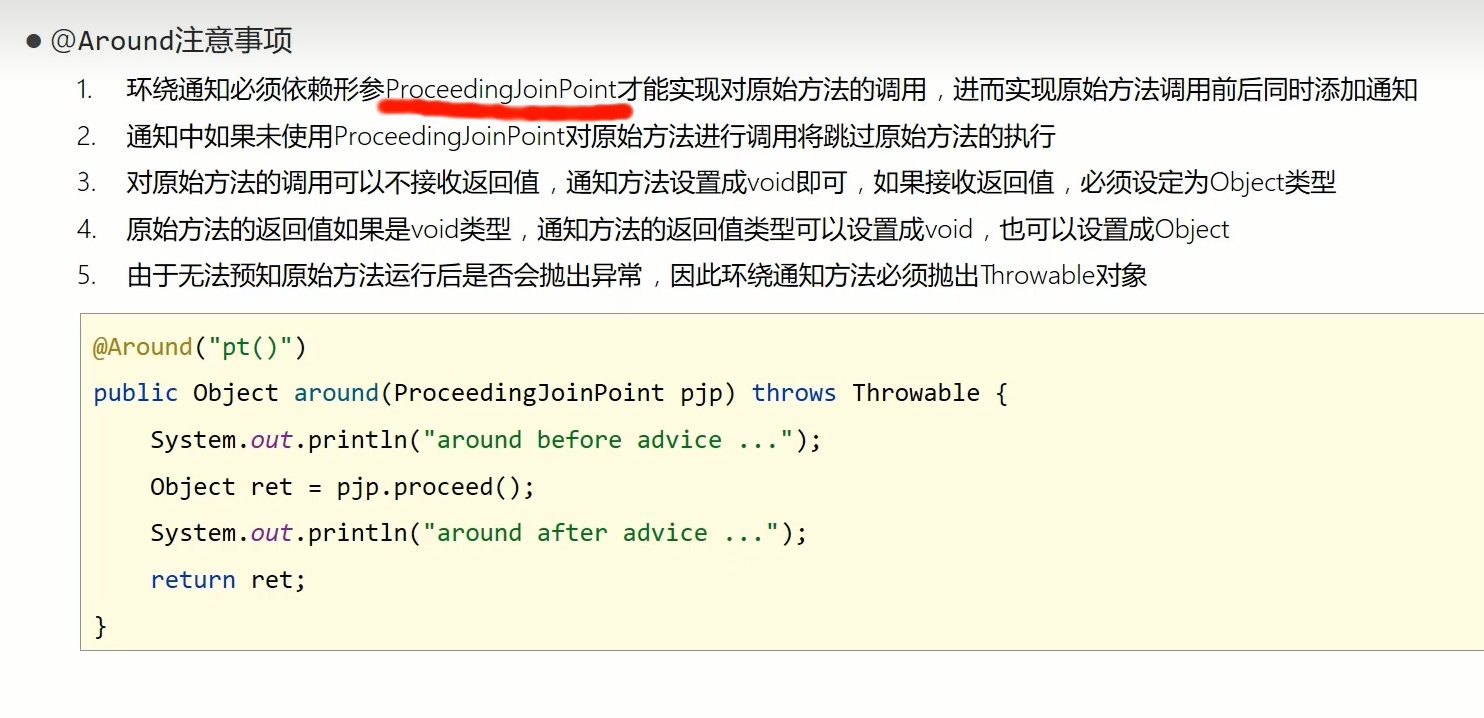
Spring——AOP切入点表达式和AOP通知类型
切入点:要进行增强的方法 切入点表达式:要进行增强的方法的描述式 第一种方法的本质是基于接口实现的动态代理(jdk) 第二种是基于cglib实现的动态代理 AOP切入点表达式 而需要加载多个切入点时,不可能每个切入点都写一个切入点表达式 例子 下面的代理描述的是匹配…...

Hadoop学习:Yarn
1.YARN介绍 一个通用的资源管理系统和调度平台 YARN不分配磁盘,由HDFS分配 相当于一个分布式的操作系统平台,为上层MR等计算程序提供运算所需要的资源(内存、CPU等) 2.YARN三大组件 不要忘记AppMaster,他是程序内部…...

Spring Data JPA
文章目录一、Spring Data基础概念二、JPA与JDBC的相同与不同之处三、Hibernate & JPA快速搭建1.添加依赖2.实体类3.hibernate的配置文件 ——hibernate.cfg.xml四、测试——基于hibernate的持久化(单独使用)五、测试——基于JPA的持久化(…...

java List报错Method threw ‘java.lang.UnsupportedOperationException‘ exception. 解决
问题描述:List使用Arrays.asList()初始化后,再add对象时报错:Method threw java.lang.UnsupportedOperationException exception.错误示例如下: List<ExportListVO.ExportSheet> sheetVOList Arrays.asList(new ExportList…...
数据结构-用栈实现队列
前言: 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾 int pop() 从队列的开头移除并返回元素 int…...

第十四章 从 Windows 客户端控制 IRIS
文章目录第十四章 从 Windows 客户端控制 IRISIRISctlGetDirsSyntaxReturn ValuesIRISctlConfigStatusSyntaxReturn ValuesIRISctlControlSyntaxReturn Values第十四章 从 Windows 客户端控制 IRIS IRIS 为 Windows 客户端程序提供了一种机制来控制 IRIS 配置并启动 IRIS 进程…...
数据结构---双链表
专栏:数据结构 个人主页:HaiFan. 专栏简介:从零开始,数据结构!! 双链表前言双链表各接口的实现为要插入的值开辟一块空间BuyLN初始化LNInit和销毁LNDestory打印链表中的值LNPrint尾插LNPushBack和尾删LNPop…...

Windows 环境安装Scala详情
为了进一步学习Spark,必须先学习Scala 编程语言。首先开始Scala 环境搭建。温馨提示:本文是基于Windows 11 安装Scala 2.13.1 版本第一步:确保本机已经正确安装JDK1.8 环境第二步:Scala 官网下载我们所属scala版本文件。Scala 官网…...
C++ Qt自建网页浏览器
C Qt自建网页浏览器如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助!前言这篇博客针对<<C Qt自建网页浏览器>>编写代码,代码整洁,规则,易读。 学习与应用推荐首选。文…...
Flink从入门到精通系列(四)
5、DataStream API(基础篇) Flink 有非常灵活的分层 API 设计,其中的核心层就是 DataStream/DataSet API。由于新版本已经实现了流批一体,DataSet API 将被弃用,官方推荐统一使用 DataStream API 处理流数据和批数据。…...
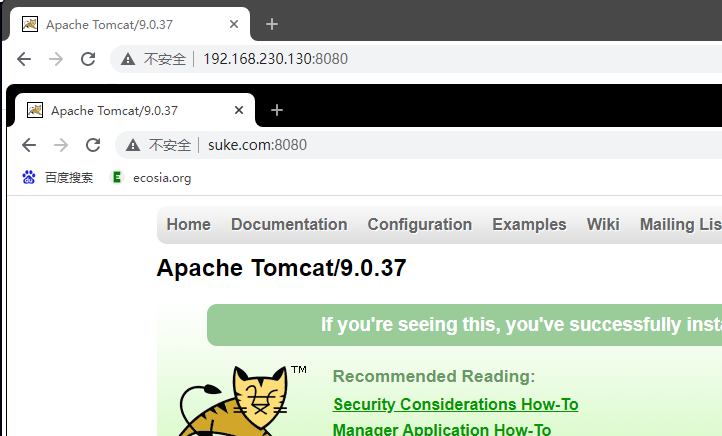
Nginx 配置实例-反向代理案例一
实现效果:使用nginx反向代理,访问 www.suke.com 直接跳转到本机地址127.0.0.1:8080 一、准备工作 Centos7 安装 Nginxhttps://liush.blog.csdn.net/article/details/125027693 1. 启动一个 tomcat Centos7安装JDK1.8https://liush.blog.csdn.net/arti…...

为什么北欧的顶级程序员数量远超中国?
说起北欧,很多人会想到寒冷的冬天,漫长的极夜,童话王国和圣诞老人,但是如果我罗列下诞生于北欧的计算机技术,恐怕你会惊掉下巴。Linux:世界上最流行的开源操作系统,最早的内核由Linus Torvalds开…...
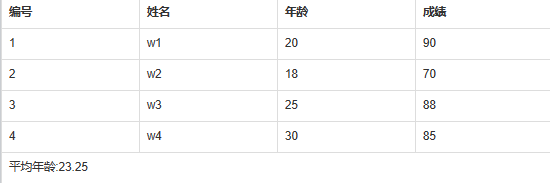
vuex getters的作用和使用(求平均年龄),以及辅助函数mapGetters
getters作用:派生状态数据mapGetters作用:映射getters中的数据使用:方法名自定义,系统自动注入参数:state,每一个方法中必须有return,其return的结果被该方法名所接收。在state中声明数据listst…...
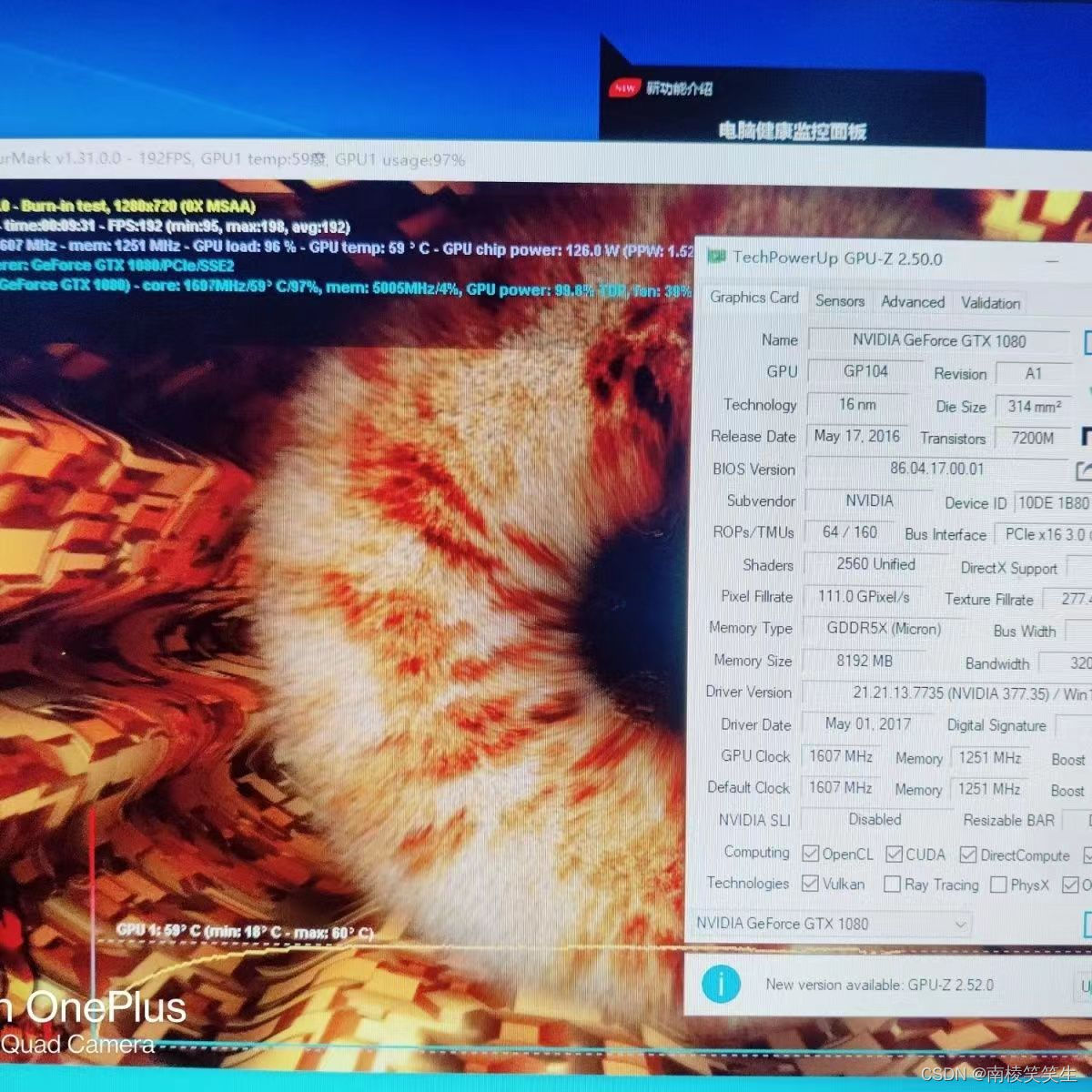
20230311给Ubuntu18.04下的GTX1080M安装驱动
20230311给Ubuntu18.04下的GTX1080M安装驱动 2023/3/11 12:50 2. 安装GTX1080驱动 安装 Nvidia 驱动 367.27 sudo add-apt-repository ppa:graphics-drivers/ppa 第一次运行出现如下的警告: Fresh drivers from upstream, currently shipping Nvidia. ## Curren…...

2023腾讯面试真题:
【腾讯】面试真题: 1、Kafka 是什么?主要应用场景有哪些? Kafka 是一个分布式流式处理平台。这到底是什么意思呢? 流平台具有三个关键功能: 消息队列:发布和订阅消息流,这个功能类似于消息…...
)
23种设计模式-建造者模式(Android应用场景介绍)
什么是建造者模式 建造者模式是一种创建型设计模式,它允许您使用相同的创建过程来生成不同类型和表示的对象。在本文中,我们将深入探讨建造者模式的Java实现,并通过一个例子来解释其工作原理。我们还将探讨如何在Android应用程序中使用建造者…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...
