ROC和AUC
目录
ROC
AUC
ROC
ROC曲线是Receiver Operating Characteristic Curve的简称,中文名为"受试者工作特征曲线"。ROC曲线的横坐标为假阳性率(False Postive Rate, FPR);纵坐标为真阳性率(True Positive Rate, TPR).FPR和TPR的计算方法分别为
FPR= FP/N
TPR = TP/P
上式中,P是真实地正样本地数量,N是真实地负样本地数量,TP是P个正样本中被分类器预测为正样本地个数,FP是N个负样本中被分类器预测为正样本地个数。
如何绘制ROC曲线?
ROC曲线是通过不断移动分类器地"截断点"来生成曲线上地一组关键点地。
在二值分类问题中,模型地输出一般都是预测样本为正例地概率。样本按照预测概率从高到底排序。在输出最终地正例、负例之前,我们需要指定一个阈值,预测概率大于该阈值地样本会判为正例,小于该阈值则会被判为负例。比如,指定阈值为0.8,那么只有第一个样本会被预测为正例,其他全部都是负例。上面所说地“截断点”指的就是区分正负预测结果地阈值。
通过动态的调整截断点,从最高地得分开始,逐渐调整到最低得分,每一个截断点都会对应一个FPR和TPR,在ROC图上绘制出每个截断点对应地位置,再连接所有点就得到最终地ROC曲线。类似于下图
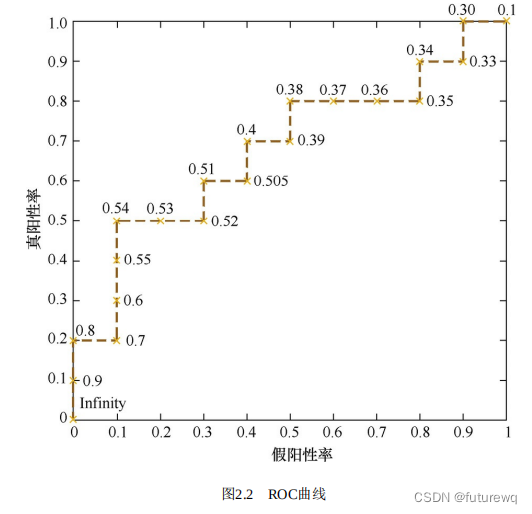
接下来用sklearn来实现。
二分类的实现
def plotROC_BinaryClass(y_true, y_score0):''':descript:绘制0-1类别的ROC曲线:param y_true: 真实标签,两个类别,[0,1]:param y_score: 预测值:return: ROC曲线'''from sklearn.metrics import roc_curve, aucfrom matplotlib import pyplot as pltfpr, tpr, thresholds = roc_curve(y_true,y_score0,pos_label=1)roc_auc = auc(fpr,tpr)plt.figure()lw = 2plt.plot(fpr, tpr, color='darkorange',lw=lw, label='ROC curve (area = %0.5f)' % roc_auc)plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')plt.xlim([0.0, 1.0])plt.ylim([0.0, 1.05])plt.xlabel('False Positive Rate')plt.ylabel('True Positive Rate')plt.title('Receiver operating characteristic example')plt.legend(loc="lower right")plt.show() 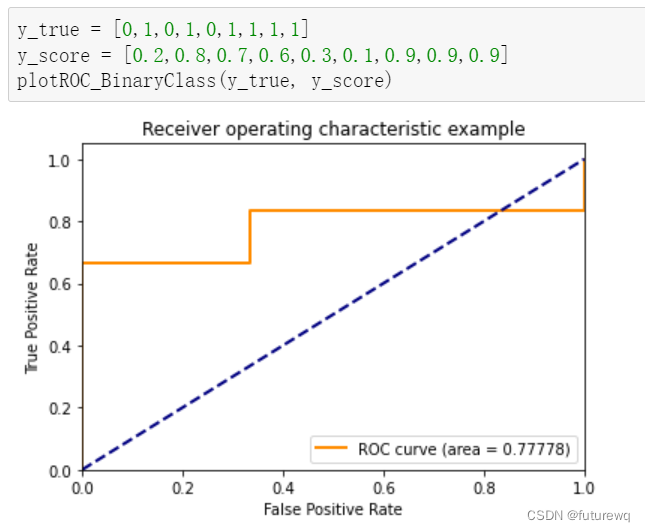
多分类的实现(每个类分开处理即可)
def plotROC_MultiClass(y_true, y_score, class_num):''':descript:绘制多类别的ROC曲线:param y_true: 真实标签,大于两个类别,[0,1,2]:param y_score: 预测值:return: ROC曲线'''from sklearn.metrics import roc_curve,aucfrom sklearn.preprocessing import label_binarizefrom matplotlib import pyplot as plt# 标签转换为one-hotclasses = list(set(y_true)) # 类别n_classes = len(classes) # 类别数y_true = label_binarize(y_true, classes)
# y_score = label_binarize(y_score, classes)fpr = dict()tpr = dict()roc_auc = dict()for i in range(n_classes):fpr[i], tpr[i], _ = roc_curve(y_true[:,i],y_score[:,i],pos_label=1)roc_auc[i] = auc(fpr[i],tpr[i])plt.figure()# Plot of a ROC curve for a specific classplt.plot(fpr[class_num], tpr[class_num], color='darkorange',lw=2,label='ROC curve (area = %0.2f)' % roc_auc[class_num]) # 绘制类别one-hot中索引为2位置的类别ROC曲线plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')plt.xlim([0.0, 1.0])plt.ylim([0.0, 1.05])plt.xlabel('False Positive Rate')plt.ylabel('True Positive Rate')plt.title('Receiver operating characteristic example')plt.legend(loc="lower right")plt.show() 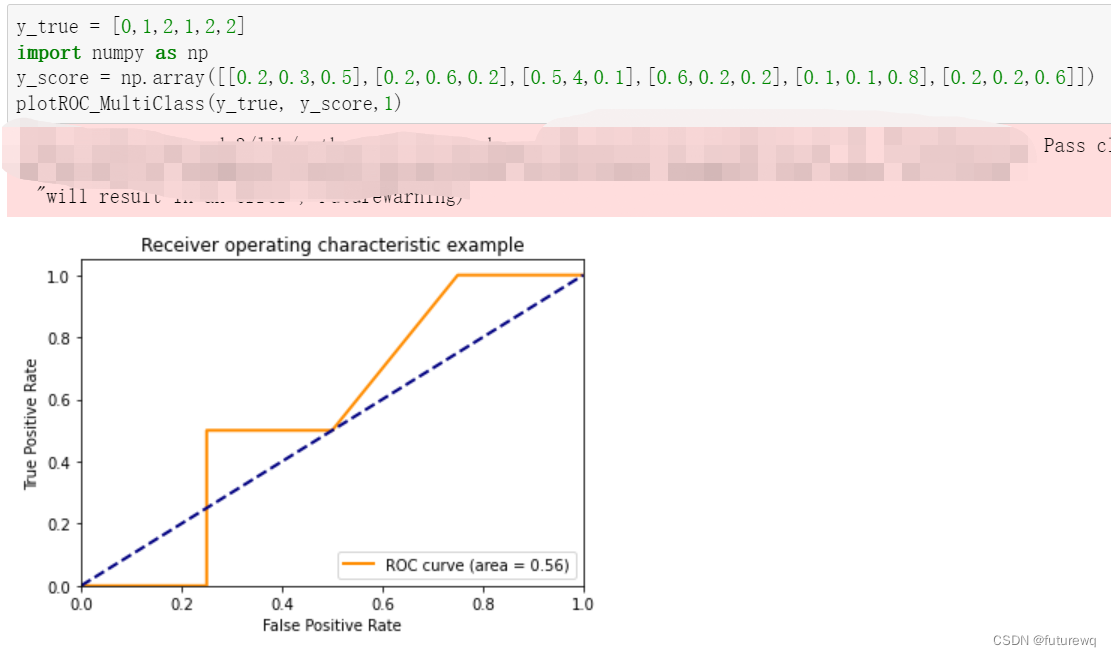
AUC
AUC指的是ROC曲线下的面积大小,该值能够量化的反映基于ROC曲线衡量出的模型性能。
AUC的物理意义:正样本的预测结果大于负样本的预测结果的概率。所以AUC反映的是分类器对样本的排序能力。
插入一个重要问题。为什么说ROC和AUC都能应用于非均衡的分类问题?
ROC曲线只与横坐标(FPR)和纵坐标(TPR)有关系。我们可以发现TPR只是正样本中预测正确的概率,而FPR只是负样本中预测错误的概率,和正负样本的比例没有关系,因此ROC的值与实际的正负样本比例无关,因此既可以用于均衡问题,也可以用于非均衡问题。而AUC的几何意义为ROC曲线下的面积,因此也和实际的正负样本比例无关。
AUC的计算
- 法1:AUC为ROC曲线下的面积,那我们直接计算面积可得。面积为一个个小的梯形面积(曲线)之和。计算的精度与阈值的精度有关 。理论性质的,没法求解。
- 法2:根据AUC的物理意义,我们计算正样本预测结果大于负样本预测结果的概率。取n1* n0(n1为正样本数,n0为负样本数)个二元组,每个二元组比较正样本和负样本的预测结果,正样本预测结果高于负样本预测结果则为预测正确,预测正确的二元组占总二元组的比率就是最后得到的AUC。时间复杂度为O(N* M)。这个换种说法可能更利于我们后面的代码实现。首先,根据每个样本的预测概率值对真实标签进行倒序排序;然后,根据顺序,依次找到真实标签为1的样本,统计其后面样本概率值低于当前真实正样本的真实负样本的个数;最后,对所有值求和,再除以(正样本个数*负样本个数)
- 法3:我们首先把所有样本按照score排序,依次用rank表示他们,如最大score的样本,rank=n (n=n0+n1,其中n0为负样本个数,n1为正样本个数),其次为n-1。那么对于正样本中rank最大的样本,rank_max,有n1-1个其他正样本比他score小,那么就有(rank_max-1)-(n1-1)个负样本比他score小。其次为(rank_second-1)-(n1-2)。最后我们得到正样本大于负样本的概率为 :
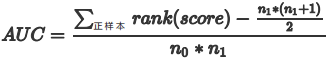
其计算复杂度为O(N+M) 。法3换种说法,有利于我们代码实现。首先,根据每个样本的预测概率对真实标签样本从小到大排序;然后,根据顺序,依次找到真实标签为1的样本,记录其(索引值+1)即上式中的rank,再按照上面的公式计算即可。
法2实现
def auc(y_true, y_pred):data = zip(y_true, y_pred)data = sorted(data, key=lambda x: x[1], reverse=True)data1 = [x[0] for x in data]true_posLabel = np.sum(y_true)true_negLabel = len(y_true) - true_posLabelcount = 0for i in range(len(y_true)):if data[i][0] == 1:j = i+1while j < len(data) and data[j][1] >= data[i][1]: # 这里直接忽略了概率相等时取0.5的情况j += 1count += (len(y_true) - j - np.sum(data1[j:]))return count/(true_negLabel * true_posLabel)法3实现:
def calAUC3(y_pred, y_true):f = list(zip(y_pred.tolist(),y_true.tolist()))rank = [values2 for values1,values2 in sorted(f,key=lambda x:x[0])]rankList = [i+1 for i in range(len(rank)) if rank[i]==1]posNum = 0negNum = 0for i in range(len(y_true)):if(y_true[i]==1):posNum+=1else:negNum+=1auc = 0auc = float(sum(rankList)- (posNum*(posNum+1))/2)/(posNum*negNum)return auc 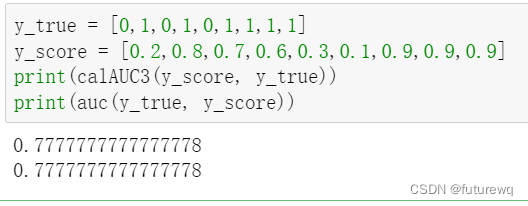
AUC和ROC是不平衡数据集中最常用的指标之一。
对于其他的评价指标需要时再整理把。
机器学习评估指标 - 知乎
机器学习评估与度量指标 - 知乎
相关文章:

ROC和AUC
目录 ROC AUC ROC ROC曲线是Receiver Operating Characteristic Curve的简称,中文名为"受试者工作特征曲线"。ROC曲线的横坐标为假阳性率(False Postive Rate, FPR);纵坐标为真阳性率(True Positive Rate, TPR).FPR和TPR的计算方法分别为 F…...

Dopamine-PEG-cRGD,DOPA-PEG-cRGD,多巴胺-聚乙二醇-crgd细胞穿膜肽
名称:多巴胺-聚乙二醇-cRGD穿膜肽,多巴胺-聚乙二醇-crgd细胞穿膜肽英文名称:Dopamine-PEG-cRGD,DOPA-PEG-cRGD规格:50mg,100mg,150mg(根据要求可定制)描述:cRGD多肽序列: cyclo(RGDfK)外 观 : 半固体或固体,取决于分子量。溶解性:…...
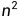
动态规划回文子串
647. 回文子串方法:双指针回文子串有长度为奇数和偶数两种,extend(s, i, i, n); extend(s, i, i 1, n);就分别对应长度为奇数和偶数的情况class Solution { private:int extend(const string& s, int i, int j, int n) {int res 0;while (i > 0…...

windows 域控提权CVE-2014-6324CVE-2020-1472CVE-2021-42287CVE-2022-26923
一、CVE-2014-6324复现 环境:god.org域,两台主机,一台win2008域控,另一台web服务器win2008 工具:ms14-068.exe(漏洞exp) mimikatz psexec 利用条件: 1.域用户账号密码 2.获得一台主机权限(本地administ…...
1、JDK 安装 Java环境变量配置
jdk下载(Java8) (下载时间不同,小版本号会有变化,不影响后续安装) 官网下载地址:https://www.oracle.com/java/technologies/downloads/#java8-windows 下载完后安装 JDK 环境变量配置 Win…...
[c++]list模拟实现
目录 前言: 学习类的方式: 1 类成员变量 1.1 list成员变量 1.2 结点结构体变量 1.3 迭代器成员变量 2 默认函数——构造 2.1 结点结构体构造函数 2.2 list构造函数 2.3 迭代器构造函数 3 迭代器实现 3.1 list部分 3.2 迭代器结构体部分 3.2…...

实用的仓库管理软件有哪些,盘点2023年5大仓库管理软件!
对于做批发生意的老板或工厂老板来说,选择一款实用的仓库管理软件是至关重要的。仓库管理软件除了可以帮你降低仓库管理成本,提高经营管理的效率,还能够在手机上随时随地掌控仓库员工和商品的最新信息,与客户、供应商的订单情况能…...
透彻研究通过explain命令得到的SQL执行计划(1))
(八十二)透彻研究通过explain命令得到的SQL执行计划(1)
今天我们正式进入研究explain命令得到的SQL执行计划的内容了,只要把explain分析得到的SQL执行计划都研究透彻,完全能看懂,知道每个执行计划在底层是怎么执行的,那么后面学习SQL语句的调优就非常容易了。 首先,我们现在…...
【Linux】旋转锁 | 读写锁
在之前的线程学习中,用到的锁都是挂起等待锁,如果申请不到锁,那就会在锁中等待; 自旋锁则不大相似 文章目录1.自旋锁1.1 概念1.2 接口1.2.1 pthread_spin_init/destroy1.2.2 pthread_spin_lock1.2.3 pthread_spin_unlock2.读写锁…...
EasyExcell导出excel添加水印
EasyExcell导出excel添加水印1、添加easyExcel相关依赖2、准备基础工具类3、创建水印handler类4、创建单元测试类WriteTest.class5、测试结果1、添加easyExcel相关依赖 <dependency><groupId>org.apache.poi</groupId><artifactId>poi</artifactId&…...

SpringCloud:Nacos配置管理
Nacos除了可以做注册中心,同样可以做配置管理来使用。 1.1.统一配置管理 当微服务部署的实例越来越多,达到数十、数百时,逐个修改微服务配置就会让人抓狂,而且很容易出错。我们需要一种统一配置管理方案,可以集中管理…...
正则表达式引擎NFA自动机的回溯解决方案总结
前几天线上一个项目监控信息突然报告异常,上到机器上后查看相关资源的使用情况,发现 CPU 利用率将近 100%。通过 Java 自带的线程 Dump 工具,我们导出了出问题的堆栈信息。 我们可以看到所有的堆栈都指向了一个名为 validateUrl 的方法&#…...

卷积神经网络之AlexNet
目录概述AlexNet特点激活函数sigmoid激活函数ReLu激活函数数据增强层叠池化局部相应归一化DropoutAlexnet网络结构网络结构分析AlexNet各层参数及其数量模型框架形状结构关于数据集训练学习keras代码示例概述 由于受到计算机性能的影响,虽然LeNet在图像分类中取得了…...

React中setState什么时候是同步的,什么时候是异步的?
本文内容均针对于18.x以下版本 setState 到底是同步还是异步?很多人可能都有这种经历,面试的时候面试官给了你一段代码,让你说出输出的内容,比如这样: constructor(props) {super(props);this.state {val: 0}}compo…...

优秀开源软件的类,都是怎么命名的?
日常编码中,代码的命名是个大的学问。能快速的看懂开源软件的代码结构和意图,也是一项必备的能力。 Java项目的代码结构,能够体现它的设计理念。Java采用长命名的方式来规范类的命名,能够自己表达它的主要意图。配合高级的 IDEA&…...

绘制CSP的patterns矩阵图
最近在使用FBCSP处理数据,然后就想着看看处理后的样子,用地形图的形式表现出来,但是没有符合自己需求的函数可以实现,就自己尝试的实现了一下,这里记录一下,方便以后查阅。 绘制CSP的patterns矩阵图 对数据做了FBCSP处理,但是想画一下CSP计算出来的patterns的地形图,并…...
Datatables展示数据(表格合并、日期计算、异步加载数据、分页显示、筛选过滤)
系列文章目录 datatable 自定义筛选按钮的解决方案Echarts实战案例代码(21):front-endPage的CJJTable前端分页插件ajax分页异步加载数据的解决方案 文章目录系列文章目录前言一、html容器构建1.操作按钮2.表格构建二、时间日期计算三、dataTables属性配置1.调用2.过…...

Python decimal模块的使用
Python decimal 模块Python中的浮点数默认精度是15位。Decimal对象可以表示任意精度的浮点数。getcontext函数用于获取当前的context环境,可以设置精度、舍入模式等参数。#在context中设置小数的精度 decimal.getcontext().prec 100通过字符串初始化Decimal类型的变…...

pycharm常用快捷键
编辑类: Ctrl D 复制选定的区域或行 Ctrl Y 删除选定的行 Ctrl Alt L 代码格式化 Ctrl Alt O 优化导入(去掉用不到的包导入) Ctrl 鼠标 简介/进入代码定义 Ctrl / 行注释 、取消注释 Ctrl 左方括号 快速跳到代码开头 Ctrl 右方括…...

useCallback 与 useMemo 的区别 作用
useCallback 缓存钩子函数,useMemo 缓存返回值(计算结果)。 TS声明如下:type DependencyList ReadonlyArray<any>;function useCallback<T extends (...args: any[]) > any>(callback: T, deps: DependencyList)…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
