0109二分图-无向图-数据结构和算法(Java)
文章目录
- 1 概念
- 2 API
- 3 分析和实现
- 4 测试
- 5 总结
- 后记
1 概念
二分图是一种能将所有结点分为两部分的图,其中图的每条边所连接的两个顶点都分别属于不同的部分。
2 API
| public class | Bipartite | |
|---|---|---|
| Bipartite(Graph G) | 预处理函数 | |
| public boolean | isBipartitle() | 是否是二分图 |
| public Iterable<Iteratable> | cycle() | 如果不是二分图,输出同色边所在环路 |
| public boolean | color(int v) | 输出顶点v的颜色 |
3 分析和实现
深度优先非递归实现,源代码如下:
package com.gaogzhen.datastructure.graph.undirected;import com.gaogzhen.datastructure.stack.Stack;
import edu.princeton.cs.algs4.Graph;import java.util.Iterator;/*** 二分图* @author: Administrator* @createTime: 2023/03/10 19:27*/
public class Bipartite {/*** 标记顶点*/private boolean[] marked;/*** 记录所有顶点到起点的路径*/private int[] edgeTo;/*** 双色标记顶点颜色,true和false*/private boolean[] color;/*** 是否是二分图标志,默认true*/private boolean isBipartite = true;/*** 如果不是二分图,记录形成同色边所在环*/private Stack<Integer> cycle;/*** 染色法检测是否是二分图** @param G the undirected graph*/public Bipartite(Graph G) {// 只是检测二分图可以不进行平行边的判断;如果想找到形成同色边所在环则需要进行平行边的判断// if (hasParallelEdges(G)) {// return;// }// don't need special case to identify self-loop as a cycle// if (hasSelfLoop(G)) return;int len = G.V();marked = new boolean[len];color = new boolean[len];edgeTo = new int[len];for (int i = 0; i < len; i++) {edgeTo[i] = -1;}dfs(G);}private void dfs(Graph G) {Stack<Node> stack = new Stack<>();for (int v = 0; v < G.V(); v++) {if (!marked[v]) {if (dfs(G, v, stack) ) {return;}}}}/*** 深度优先染色** @param G 无向图* @param v* @param stack*/private boolean dfs(Graph G, int v, Stack<Node> stack) {marked[v] = true;Iterable<Integer> adj = G.adj(v);if (adj != null) {stack.push(new Node(v,adj.iterator()));}while (!stack.isEmpty()) {Node c = stack.pop();while (c.adj.hasNext()) {Integer w = c.adj.next();if (!marked[w]) {marked[w] = true;edgeTo[w] = c.v;// 当前顶点染和其父结点相反的颜色color[w] = !color[c.v];if (c.adj.hasNext()) {stack.push(c);}Iterable<Integer> adjW = G.adj(w);if (adjW != null) {stack.push(new Node(w, adjW.iterator()));}break;}// check for cycle (but disregard reverse of edge leading to v)else if (color[w] == color[c.v]) {// 记录同色边所在环路cycle = new Stack<>();cycle.push(w);for (int x = c.v; x != w; x = edgeTo[x]) {cycle.push(x);}cycle.push(w);isBipartite = false;return true;}}}return false;}/*** 检测无向图G是否有子环* @param G* @return*/private boolean hasSelfLoop(Graph G) {for (int v = 0; v < G.V(); v++) {for (int w : G.adj(v)) {if (v == w) {cycle = new Stack<Integer>();cycle.push(v);cycle.push(v);return true;}}}return false;}/*** 检测无向图G是否有平行边* @param G* @return*/private boolean hasParallelEdges(Graph G) {marked = new boolean[G.V()];for (int v = 0; v < G.V(); v++) {// check for parallel edges incident to vfor (int w : G.adj(v)) {if (marked[w]) {cycle = new Stack<Integer>();cycle.push(v);cycle.push(w);cycle.push(v);return true;}marked[w] = true;}// reset so marked[v] = false for all vfor (int w : G.adj(v)) {marked[w] = false;}}return false;}/*** 是否是二分图* @return*/public boolean isBipartite() {return isBipartite;}public boolean color(int v) {validateVertex(v);if (!isBipartite) {throw new UnsupportedOperationException("graph is not bipartite");}return color[v];}private void validateVertex(int v) {int V = marked.length;if (v < 0 || v >= V) {throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));}}/*** 如果有环,返回环路* @return a cycle if the graph {@code G} has a cycle,* and {@code null} otherwise*/public Iterable<Integer> cycle() {return cycle;}static class Node {/*** 顶点索引*/private int v;/*** 顶点邻接表*/private Iterator<Integer> adj;public Node(int v, Iterator<Integer> adj) {this.v = v;this.adj = adj;}}
}
原理:深度优先遍历无向图,遍历顶点v,标记且颜色染为其父结点的反色。遍历顶点v邻接表顶点w时,如果w已经被标记过且颜色和顶点v的颜色相同。说明边v-w为同色边,不是二分图。重复上述过程,如果遍历完整个无向图,没有发现同色边,说明该无向图为二分图,且染色完毕。
记录同色边所在环:edgeTo[]记录所有顶点到起点的路径,为一棵由父链接表示的树。如果找到同色边v-w,说明它一也形成了环路。变量从顶点v开始遍历树,通过把x设为edgeTo[v],直到顶点w。容器起始放入顶点w,最后放入w,记录完整环路。
双色:利用布尔值true和false表示,通过逻辑非很容易取反色。
4 测试
测试代码:
public static void testBipartite() {String path = "H:\\gaogzhen\\java\\projects\\algorithm\\asserts\\bipartite.txt";// String path = "H:\\gaogzhen\\java\\projects\\algorithm\\asserts\\maze.txt";In in = new In(path);Graph graph = new Graph(in);Bipartite bipartite = new Bipartite(graph);System.out.println("是否是二分图:" + bipartite.isBipartite());System.out.println("非二分图环:" + bipartite.cycle());
}
bipartite.txt中染色效果如下图4-1所示:

maze.txt染色效果如下图4-2所示:

5 总结
如果一幅图有环且环中顶点数为奇数,那么它就不是二分图。
- 如果一幅图没有环,那么深度优先遍历就是一棵树,从起点开始,把边两个顶点染不同的颜色,一定是二分图。
- 一幅图有环而且环中顶点数为奇数,给顶点做标记1,2,…,2k+1,k∈N1,2,\dots,2k+1,k\in N1,2,…,2k+1,k∈N。根据我们的染色规则,那么第1和顶点和最后一个顶点由同一条边相连接,且颜色相同。所以不是二分图。
广度优先搜索算法也可以解决二分图判别染色问题,有兴趣的小伙伴自行实现吧,也可以参考算法第四版对应jar包。
后记
如果小伙伴什么问题或者指教,欢迎交流。
❓QQ:806797785
⭐️源代码仓库地址:https://gitee.com/gaogzhen/algorithm
参考链接:
[1][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法:第4版[M].北京:人民邮电出版社,2012.10.p344-348.
相关文章:

0109二分图-无向图-数据结构和算法(Java)
文章目录1 概念2 API3 分析和实现4 测试5 总结后记1 概念 二分图是一种能将所有结点分为两部分的图,其中图的每条边所连接的两个顶点都分别属于不同的部分。 2 API public classBipartiteBipartite(Graph G)预处理函数public booleanisBipartitle()是否是二分图pub…...
)
计算机网络题库---选择题刷题训练(100多道精品)
第一章 概述 1.下列四项内容中,不属于Internet(因特网)基本功能是___D_____。 A.电子邮件 B.文件传输 C.远程登录 D.实时监测控制 2.Internet是建立在____C_____协议集上的国际互联网络。 A.IPX B.NetBEUI C.TCP/IP …...

16、字符串生成器
目录 (1)append()方法 (2)insert(int offset, arg)方法 (3)delete(int start , int end)方法 创建成功的字符串对象,其长度是固定的,内容不能被改变和编译。虽然使用“”可以达到…...

docker基本命令-容器
容器 基本概念 镜像(Image)和容器(Container)的关系,就像是面向对象程序设计中的 类 和 实例 一样,镜像是静态的定义,容器是镜像运行时的实体。容器可以被创建、启动、停止、删除、暂停等。 容…...
QT入门基础(一)
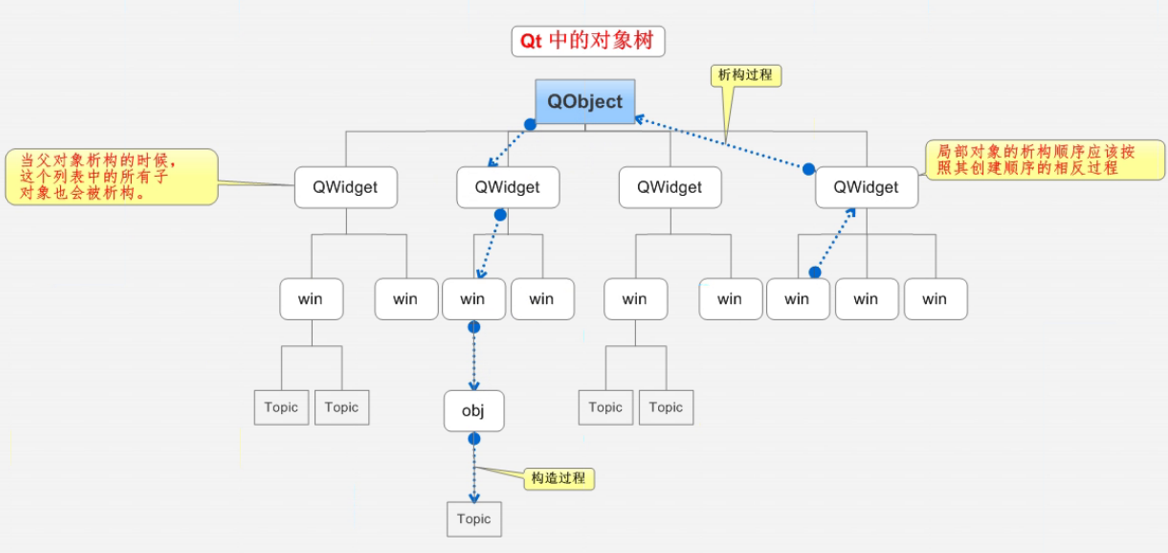
文章目录零.Qt背景1.什么是Qt2.Qt的发展史3.Qt的优势4.Qt应用一.第一个Qt程序0.项目创建1.main函数文件2.类头文件3.pro文件4.qt命名规范二.Qt按钮1.按钮创建和父子关系2.按钮常用api3.Qt窗口坐标体系4.对象树模型零.Qt背景 1.什么是Qt Qt是一个跨平台的C图形用户界面应用程序…...
WattOS:一个稳又快的轻量级 Linux 发行版
导读Linux 领域里的每个人不是听说过就是使用过某个轻量级的 Linux 发行版。大家都知道我们不断追求的是:占用内存少,配置资源要求低,包含一个轻量级的桌面环境(或者窗口管理器),并且提供和其他发行版相似的…...

Java调用Python脚本:轻松实现两种语言的互操作性
Java和Python都是非常流行的编程语言,它们都有自己的优点,但也有自己的局限性。在编写应用程序时,我们可能需要使用两种语言来共同完成一项任务。在这种情况下,Java需要调用Python脚本来解决某些问题,同时利用Java和Py…...
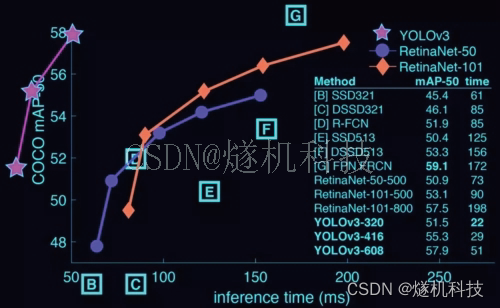
未系安全带识别系统 yolo
未系安全带识别系统通过pythonyolo智能视频分析技术,未系安全带识别算法对画面中高空作业人员未系安全带行为进行监测,未系安全带识别算法监测到人员未穿戴安全带时,立即通知后台人员及时处理触发告警。Yolo算法采用一个单独的CNN模型实现end…...
大白话MySQL是如何根据成本优化选择执行计划的?(上))
(七十六)大白话MySQL是如何根据成本优化选择执行计划的?(上)
之前已经给大家讲解清楚了 MySQL 在执行单表查询时候的一些执行计划,比如说const、ref、range、index、all之类的,也讲了多表关联的时候是如何执行的,本质其实就是先查一个驱动表,接着根据连接条件去被驱动表里循环查询࿰…...
DSRC技术
DSRC(Dedicated Short Range Communication)专用短程通信 定位 是V2X领域存在的两大通信技术之一(另一个为LTE-V2X)。 所属技术路线 与这两大技术相对应,是V2X无线通信技术的两大技术路线: IEEE 802.11p 本是04年指定的一个通…...

_面经问题_
一、Java编程语言 Java语言有哪些特点? JVM vs JDK vs JRE 什么是字节码? 采用字节码的好处是什么? 为什么不全部使用AOT呢? 为什么说Java语言"编译与解释并存"? Oracle JDK vs OpenJDK Java和C的区别? 注释有哪几种形式? 标识符和关键字的区别是什么? Jav…...
刷题记录(2023.3.6 - 2023.3.11)
我很喜欢这周的感觉,前两道题对着 wp 简略复现了一下,由于以前都是自己学习,对一些稍微多、稍微难的题都会马上避开,笨小孩逃避太久了,有些事逃不掉,总得面对,开始往往很难,多花点时…...
14 Day:同步锁与操作系统输入输出
前言:在上一期的线程章节中,我们的线程输出貌似有大问题,今天我们便要来学习同步锁来解决这个问题,同时再次基础上拿下键盘输入,实现操作系统的输入和输出。从今天开始我们的操作系统不在是一块“看板”了!…...

Gradle 的下载安装教程
Gradle 8.0.1 下载安装教程笔者的环境: Java 17.0.1 Gradle 8.0.1 Windows 10 教育版 64位 在继续阅读本教程之前,需要先完成 JDK 的安装。JDK 需要选择 8 及以上的版本。关于 JDK 的安装,可见笔者的另一篇博客: Java 的下载安…...

「Python 基础」常用模块
文章目录1. 内建模块datetimecollectionsnamedtuple()dequedefaultdictOrderedDictChainMapCounterbase64structhashlib摘要算法摘要的应用hmacitertoolscontextlib\_\_enter\_\_ 和 \_\_exit\_\_contextmanagerclosingurllibGETPOSTHandlerXMLDOMSAXHTMLParser2. 第三方模块Pi…...

Java【二叉搜索树和哈希表】详细图解 / 模拟实现 + 【Map和Set】常用方法介绍
文章目录前言一、二叉搜索树1、什么是二叉搜索树2、模拟实现二叉搜索树2.1, 查找2.2, 插入2.3, 删除3、性能分析二、模型三、哈希表1、什么是哈希表1.1, 什么是哈希冲突1.2, 避免, 解决哈希冲突1.2.1, 避免: 调节负载因子1.2.2, 解决1: 闭散列(了解)1.2.3, 解决2: 开散列/哈希桶…...

如何用 C 语言实现文本特征提取?
文本特征提取是一种将文本转换为数字或向量表示的技术,它是自然语言处理中的重要步骤。以下是一些用 C 语言实现文本特征提取的基本方法:基于词袋模型的特征提取词袋模型是一种将文本表示为单词频率的方法,可以通过以下步骤实现:将…...

ESD静电保护器件分类简介及场景应用
文章目录 1. ESD介绍1.1 ESD简介1.2 ESD产生原理1.3 ESD危害2. 器件级ESD模型2.1 人体模型(HBM)2.2 机器模型(MM)2.3 带电器件模型(CDM)3. 系统级ESD模型3.1 介绍3.2 防护器件分类简介3.2.1 TVS二极管3.2.2 MLCC陶瓷电容3.2.3 ESD抑制管3.2.4 MOV压敏电阻3.2.5 比较4. ES…...

硅谷银行倒闭的几点启示
摘要:本文从公开资料分析一下硅谷银行对信息科技行业的我们有一些什么启示。硅谷银行“拔网线”了,想创业的您,该注意了。1.硅谷银行是谁我们从其官网的说明来看看。The financial partner of the innovation economy.(翻译成中文…...

【AWS入门】IAM基本应用-2023/3/4
目录IAM概述根用户和IAM用户参考IAM概述 IAM(Identity Access Management)是身份和访问管理服务,要访问AWS服务和资源,就要使用IAM进行身份验证和授权。当我们通过控制台,CLI,或API访问AWS服务时,都需要通…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
