【离散数学·图论】(复习)
一、基本概念
1.一些基本术语:

2.点u,v邻接(或相邻): 边e称为关联顶点u和v,or e连接u和v;
3.G=(V,E)中,顶点v所有邻居的集合:N(v), 成为v的邻域。
4.度 : deg(v)
5.悬挂点:度为1的顶点;
6.孤立点:度为0的顶点。
二、几个定理and概念
1.握手定理:边数的2倍=度数。 (总度数一定为偶数)
2.无向图有偶数个奇数度顶点。 (由1.) (定理2)
3.入度: ; 出度:
4.有向图,边数=入度=出度 (定理3)
5.完全图: , 每个顶点的度:n-1
6.圈图:
7.轮图: 顶点数:n+1,边数:2n
8.立方体图: 顶点数:2^n,边数: n*(2^(n-1))
9.二部图(二分图):用颜色判断
10.完全二部图
11.从旧图到新图: (子图,并图等)
12.加权图 : 边上带权重
三、图的表示
1.邻接表

2.邻接矩阵
3.关联矩阵:
当ej关联vi时 :1;or : 0;

四、其它概念
1.图的同构:
对于G1(V1,E1),G2(V2,E2) ,存在映上的从V1到V2 的函数f;
f性质:对所有a,b a和b在G1里相邻<->a和b在G2里相邻。
2.通路:从u到v, (边的序列)
长度:通路中边的数目
对于权重图,则为各边的权重之和。
回路:若一条通路在相同的顶点开始和结束,且长度大于0,则它是一条回路。
若通路或回路不重复的包含相同的边,那么它就是简单的。
各边全不同的:简单回路;
各点全不同的:基本回路;
3.可达性:vi到vj从在通路(不管长度)。
4.无向图连通性:
连通图:每一对顶点间都有一条路径;
or : 不连通图;
5.连通分量:是G的连通子图,而不是G的其它连通子图的真子图。(即G的最大连通子图)
6.有向图连通性:
(1)强连通:对任意a,b a到b有,b到a也有;
(2)弱连通:在有向图的基本无向图中是连通的;
7.计算顶点间的通路:用矩阵相乘。
五、欧拉回/通路 (可一笔画出) (边不重复)
1.欧拉回路 充要: 所有顶点度数都为偶数;
2.欧拉通路 充要:有2个顶点度数为奇数,其它为偶数。
六、哈密顿回/通路 (点不重复) (无充要条件)
1.哈回=>.... (性质)
定理:

2....=>哈
定理:

3....=>哈回
(1)狄拉克定理:

(2)奥尔定理:

例:![]()
答:m=n>=2;
七、平面图与着色:
1.欧拉公式:
设G是带e条边和v个顶点的连通平面简单图。设r是G的平面图表示中的面数,则 r=e-v+2。
2.图着色
简单图的着色:给每个顶点都指定一种颜色,使没有两个相邻的顶点颜色相同。
(平面图的着色数不超过4)
相关文章:

【离散数学·图论】(复习)
一、基本概念 1.一些基本术语: 2.点u,v邻接(或相邻): 边e称为关联顶点u和v,or e连接u和v; 3.G(V,E)中,顶点v所有邻居的集合:N(v), 成为v的邻域。 4.度 : deg(v) 5.悬挂点:度为1的…...

【ONLYOFFICE震撼8.1】ONLYOFFICE8.1版本桌面编辑器测评
随着远程工作的普及和数字化办公的发展,越来越多的人开始寻找一款具有强大功能和便捷使用的办公软件。在这个时候,ONLYOFFICE 8.1应运而生,成为了许多用户的新选择。ONLYOFFICE 8.1是一种办公套件软件,它提供了文档处理、电子表格…...

Shell 脚本编程保姆级教程(上)
一、运行第一个 Shell 脚本 1.1 Shell 脚本 Shell 脚本(shell script),是一种为 shell 编写的脚本程序。 业界所说的 shell 通常都是指 shell 脚本,但读者朋友要知道,shell 和 shell script 是两个不同的概念。 由…...

凸优化相关文章汇总
深度学习/机器学习入门基础数学知识整理(三):凸优化,Hessian,牛顿法_深度学习和凸优化-CSDN博客 深度学习/机器学习入门基础数学知识整理(四):拟牛顿法、BFGS、L-BFGS、DFP、共轭梯…...
Java鲜花下单预约系统源码小程序源码
让美好触手可及 🌸一、开启鲜花新篇章 在繁忙的都市生活中,我们总是渴望那一抹清新与美好。鲜花,作为大自然的馈赠,总能给我们带来无尽的惊喜与愉悦。但你是否曾因为工作繁忙、时间紧张而错过了亲自挑选鲜花的机会?今…...

网络变压器和RJ45接线的方法
网络变压器在以太网硬件电路设计中扮演着重要的角色,它主要用于信号电平耦合、隔离外部干扰、实现阻抗匹配以及增加传输距离。而RJ45接口则是以太网连接的标准化接口,它提供了与网络电缆的连接点。 网络变压器与RJ45的接线方法通常遵循以下步骤…...

Matlab/simulink三段式电流保护
电流1段仿真波形如下所示 电流2段仿真波形如下所示 电流3段仿真波形如下所示...

OOXML入门学习
进入-飞入 <par> <!-- 这是一个并行动画序列的开始。"par"代表并行,意味着在这个标签内的所有动画将同时开始。 --><cTn id"5" presetID"2" presetClass"entr" presetSubtype"4" fill"hold&…...

k8s集群node节点加入失败
出现这种情况: [preflight] FYI: You can look at this config file with kubectl -n kube-system get cm kubeadm-config -o yaml [kubelet-start] Writing kubelet configuration to file "/var/lib/kubelet/config.yaml" [kubelet-start] Writing kub…...

layui+jsp项目中实现table单元格嵌入下拉选择框功能,下拉选择框可手动输入内容或选择默认值,修改后数据正常回显。
需求 table列表中的数据实现下拉框修改数据,当默认的下拉框不符合要求时,可手动输入内容保存。内容修改后表格显示修改后的值同时表格不刷新。 实现 layui框架下拉框组件只能选择存在的数据,不支持将输入的内容显示在input中的功能&#x…...

2024年客户体验的几个预测
数字化转型、以客户为中心的理念、数字技术的发展和产品的不断创新,都为客户体验带来了巨大的改变。 目前,我们看到很多公司都在致力于塑造一种以客户为中心的商业模式。企业开始用更多技术、更多数据和更多产品来强化自己在客户体验方面的能力。 那么&a…...
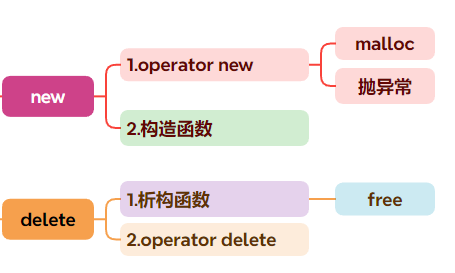
【C++】动态内存管理new和delete
文章目录 一、C的内存管理方式二、new和delete的用法1.操作内置类型2.操作自定义内置类型 三、new和delete的底层实现1.operator new和operator delete函数2.new和delete的实现原理 四、定位new表达式五、malloc/free和new/delete的区别 一、C的内存管理方式 之前在C语言的动态…...
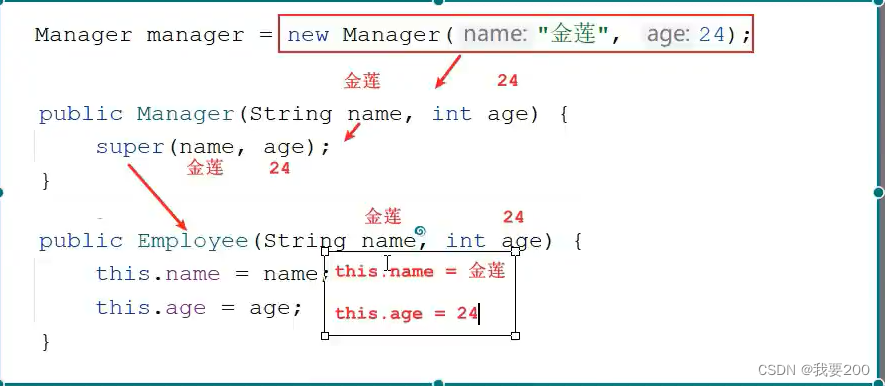
Java面向对象特性
Java继承: 继承的概念: 在Java中,继承(inheritance)是面向对象编程的一个重要概念,它允许一个类(子类)继承另一个类(父类)的属性和方法。通过继承,…...
odoo17 tree视图添加按钮
需求描述 点击下图中tree视图上的同步退货单按钮,弹出相应的form视图进行退货单同步,然后点击同步按钮调用后端python代码处理。 实现步骤 主要文件目录结构 js文件的创建 /** @odoo-module **/ import {registry } from "@web/core/registry"; import {listVie…...

PreparedStatement 与Statement 的区别,以及为什么推荐使用 PreparedStatement ?
在Java中,PreparedStatement和Statement都是用于执行SQL语句的重要接口,但它们在功能、安全性和性能上有着显著的差异。理解这些差异对于编写高效且安全的数据库应用程序至关重要。 Statement:基本的SQL执行者 首先,让我们从Sta…...
wsl ubuntu 安装Anaconda3步骤
如何在Ubuntu上安装Anaconda3呢?本章记录整个安装过程。 1、下载脚本 https://mirrors.bfsu.edu.cn/anaconda/archive/Anaconda3-2023.09-0-Linux-x86_64.sh 下载之后,将脚本上传到Ubuntu里。 2、安装脚本 bash Anaconda3-2021.11-Linux-x86_64.sh根据提示进行安装,提示输…...

Vue3响应式 ref全家桶
<template><div>{{ man.name }}<hr><button click"change">修改</button></div> </template> <script setup lang"ts"> const man {name:"cc"} const change () >{man.name "大cc&q…...
Mac(M1芯片)安装多个jdk,Mac卸载jdk
1.jdk下载 oracle官方链接:oracle官方下载链接 2.安装 直接下一步,下一步就行 3.查看是否安装成功 出现下图内容表示安装成功。 4.配置环境变量 open -e .bash_profile 路径建议复制过去 #刷新环境变量 source ~/.bash_profile 5.切换方法 6.jdk…...
)
Warning message:package ‘ggplot2’ is not available (for R version 3.2.3)
install.packages(ggplot2) Installing package into ‘/usr/local/lib/R/site-library’ (as ‘lib’ is unspecified) Warning message: package ‘ggplot2’ is not available (for R version 3.2.3) 根据你提供的信息,警告消息表明在你的R版本(3.2.3…...

Spring Boot 过滤器和拦截器详解
目录 Spring Boot 过滤器1.什么是过滤器2.工作机制3.实现过滤器 Spring Boot 拦截器1. 什么是拦截器2. 工作原理3.实现4.拓展(MethodInterceptor 拦截器)实现 过滤器和拦截器区别过滤器和拦截器应用场景过滤器拦截器 Spring Boot 过滤器 1.什么是过滤器 …...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
