游戏AI的创造思路-技术基础-机器学习(2)
本篇存在大量的公式,数学不好的孩子们要开始恶补数学了,尤其是统计学和回归方程类的内容。
小伙伴们量力而行~~~~~
游戏呢,其实最早就是数学家、元祖程序员编写的数学游戏,一脉相承传承至今,囊括了更多的设计师、美术家、音乐家、作家、导演、演员等等,发展形成了今天大家看到的繁花般的多彩游戏世界。作为游戏工作者特别是游戏算法程序员,我们应当不停的学习数学知识,满足应用需求哦
大家共勉!
(后面算法先给出些简单示例和伪代码,可能有些来不及写完,后续逐步补充)

目录
4. 最常见的机器学习算法
4.1. 线性回归(Linear Regression)
4.2. 逻辑回归(Logistic Regression)
4.2.1. 逻辑回归模型
4.2.2. 损失函数
4.2.3. 优化方法
4.2.4. 算法示例
4.3. 决策树(Decision Tree)
4.3.1. 特征选择
4.3.2. 决策树生成
4.3.3. 决策树剪枝
4.3.4. 算法示例
4.4. 支持向量机(Support Vector Machine, SVM)
4.4.1. SVM 的主要概念
4.4.2. SVM 的优点
4.4.3. 算法示例
C++ 算法示例
4.5. 朴素贝叶斯(Naive Bayes)
4.5.1. 算法介绍
4.5.2. 算法示例
4.6. k-近邻算法(K-Nearest Neighbors, KNN)
4.6.1. k-近邻算法介绍
4.6.2. k-近邻算法步骤
4.6.3. 算法示例
4.7. k-平均算法(K-Means)
4.7.1. k-平均算法介绍
4.7.2. k-平均算法步骤
4.7.3. 算法示例
4.8. 庆祝下
4. 最常见的机器学习算法
最常见的机器学习算法包括线性回归、逻辑回归、支持向量机、决策树、随机森林、神经网络(包括卷积神经网络)等。机器学习的基础算法及其示例可以归纳为以下几点:
4.1. 线性回归(Linear Regression)
- 基础概念:线性回归是一种用于预测数值类型的机器学习算法,通过建立自变量和因变量之间的线性关系模型来进行预测。
- 算法示例:北京房价预测。通过收集房屋的各种特征(如面积、房间数等),使用线性回归模型来预测房价。
线性回归(Linear Regression)是一种统计学上的预测分析,用于估计两个或多个变量之间的关系。在线性回归中,目标变量(因变量)被预测为自变量的线性组合。简单来说,线性回归试图找到一条最佳拟合直线,使得预测值与实际值之间的残差平方和最小。
线性回归模型可以表示为:
其中是因变量,
是自变量,
是回归系数,
是误差项。
Python 算法示例
在 Python 中,我们通常使用 sklearn 库来进行线性回归。以下是一个简单的示例:
from sklearn.linear_model import LinearRegression
import numpy as np # 创建一些样本数据
X = np.array([[1], [2], [3], [4], [5]]) # 自变量
y = np.array([2, 4, 6, 8, 10]) # 因变量 # 创建一个线性回归模型对象
model = LinearRegression() # 使用样本数据训练模型
model.fit(X, y) # 使用模型进行预测
X_test = np.array([[6], [7]])
y_pred = model.predict(X_test) print("预测值:", y_pred)C++ 算法示例
在 C++ 中,你可能需要手动实现线性回归算法。以下是一个简单的示例,使用最小二乘法求解回归系数:
#include <iostream>
#include <vector>
#include <Eigen/Dense> int main() { // 样本数据 Eigen::MatrixXd X(5, 2); // 5个样本,每个样本有1个自变量和1个截距项(全为1) X << 1, 1, 1, 2, 1, 3, 1, 4, 1, 5; Eigen::VectorXd y(5); // 5个因变量值 y << 2, 4, 6, 8, 10; // 使用最小二乘法求解回归系数 (beta = (X'X)^(-1)X'y) Eigen::VectorXd beta = X.transpose() * X).inverse() * X.transpose() * y; // 输出回归系数 std::cout << "回归系数: " << beta.transpose() << std::endl; // 使用模型进行预测 Eigen::MatrixXd X_test(2, 2); // 2个测试样本,每个样本有1个自变量和1个截距项(全为1) X_test << 1, 6, 1, 7; Eigen::VectorXd y_pred = X_test * beta; // 进行预测 // 输出预测值 std::cout << "预测值: " << y_pred.transpose() << std::endl; return 0;
}注意:C++ 示例中使用了 Eigen 库来进行矩阵运算。你需要先安装 Eigen 库才能编译和运行此代码。你可以从 Eigen 官网下载和安装 Eigen。
这两个示例都展示了如何使用线性回归模型进行简单的预测。Python 示例使用了 scikit-learn: machine learning in Python — scikit-learn 1.5.0 documentation 库,而 C++ 示例则使用了 Eigen 库来进行矩阵运算。
4.2. 逻辑回归(Logistic Regression)
- 基础概念:逻辑回归是一种用于分类问题的机器学习算法,特别适用于二分类问题。它通过将数据映射到概率空间来进行建模。
- 算法示例:信用卡欺诈检测。通过分析信用卡交易数据,使用逻辑回归模型来预测某笔交易是否为欺诈行为。
逻辑回归(Logistic Regression)是一种广义的线性模型,用于解决二分类问题。它使用逻辑函数(也称为Sigmoid函数)将线性回归的输出映射到0和1之间,从而表示概率。逻辑回归的名字中虽然有“回归”,但它实际上是一种分类算法。
4.2.1. 逻辑回归模型
逻辑回归的模型可以表示为:
其中,是权重向量,
是特征向量,
是偏置项。这个函数将线性回归的输出
通过Sigmoid函数映射到0和1之间,表示给定特征
下,
的概率。
4.2.2. 损失函数
逻辑回归通常使用交叉熵损失函数(Cross-Entropy Loss):
其中,是样本数量,
是第
个样本的真实标签(0或1),
是模型预测的第
个样本为正类的概率。
4.2.3. 优化方法
逻辑回归通常使用梯度下降法(Gradient Descent)或其变种(如随机梯度下降SGD、小批量梯度下降Mini-Batch GD等)来优化损失函数。
4.2.4. 算法示例
Python算法示例
在Python中,我们可以使用scikit-learn库中的LogisticRegression类来实现逻辑回归:
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score # 加载数据集
iris = load_iris()
X = iris.data
y = iris.target # 将多分类问题简化为二分类问题
y = (y != 0) * 1 # 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 创建逻辑回归模型并训练
model = LogisticRegression(max_iter=1000)
model.fit(X_train, y_train) # 预测测试集并计算准确率
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy}")C++算法示例
在C++中,我们可以使用mlpack库可以从mlpack - Home官网获取哦(一个C++机器学习库)来实现逻辑回归。以下是一个简化的示例:
#include <mlpack/core.hpp>
#include <mlpack/methods/logistic_regression/logistic_regression.hpp>
#include <mlpack/methods/logistic_regression/logistic_regression_function.hpp> using namespace mlpack;
using namespace mlpack::regression;
using namespace mlpack::optimization; int main() { // 假设你已经有了一些训练数据X_train和y_train arma::mat X_train; // 特征数据,大小为N x D(N个样本,D个特征) arma::Row<size_t> y_train; // 标签数据,大小为1 x N // 创建并训练逻辑回归模型 LogisticRegressionFunction<> lrf(X_train, y_train, 0.01); // 0.01是正则化参数 LBFGS<LogisticRegressionFunction<> > optimizer; arma::vec parameters; // 模型参数将被存储在这里 optimizer.Optimize(lrf, parameters); // 训练模型 // 使用训练好的模型进行预测 LogisticRegression<> model(parameters); arma::Row<size_t> predictions; model.Predict(X_train, predictions); // 对训练集进行预测,仅作为示例 // 计算准确率等性能指标... // ... return 0;
}注意:上述C++示例代码是一个简化的模板,用于说明如何在C++中使用逻辑回归。在实际应用中,你可能需要处理数据加载、预处理、模型评估等多个方面。此外,mlpack库可能需要单独安装和配置。
4.3. 决策树(Decision Tree)
- 基础概念:决策树是一种基于树状结构的分类和回归算法,通过对数据集进行递归分割来形成决策规则。
- 算法示例:风险评估。游戏中可以用来评估玩家继续游戏的欲望程度,采取降低难度、给与奖励或激励,或提升难度,给与更大奖励刺激,以及及时给出充值付费买道具等等措施。
决策树(Decision Tree)是一种基本的分类与回归方法,它可以被认为是一个树形结构,每个内部节点表示一个属性上的判断条件,每个分支代表一个判断结果的输出,每个叶子节点代表一种分类结果。决策树学习通常包括三个步骤:特征选择、决策树生成和决策树剪枝。
4.3.1. 特征选择
特征选择在于选取对训练数据具有分类能力的特征,常用的准则有信息增益(如ID3算法)、信息增益比(如C4.5算法)和基尼指数(如CART算法)。
4.3.2. 决策树生成
根据选择的特征评估准则,从上至下递归地生成子节点,直到数据集不可分则停止。
4.3.3. 决策树剪枝
决策树容易过拟合,一般通过剪枝来简化决策树,防止过拟合。剪枝有预剪枝和后剪枝两种方法。
4.3.4. 算法示例
Python算法示例
在Python中,我们可以使用scikit-learn库中的DecisionTreeClassifier来实现决策树分类:
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score # 加载数据集
iris = load_iris()
X = iris.data
y = iris.target # 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 创建决策树模型并训练
clf = DecisionTreeClassifier(random_state=42)
clf.fit(X_train, y_train) # 预测测试集并计算准确率
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy}")C++算法示例
在C++中,实现决策树算法通常比较复杂,因为需要手动处理数据的加载、预处理、特征选择、树的构建和剪枝等步骤。不过,有一些库如mlpack也提供了决策树的实现。以下是一个使用mlpack的简化示例:
#include <mlpack/methods/decision_tree/decision_tree.hpp>
#include <mlpack/core/data/load.hpp> using namespace mlpack;
using namespace mlpack::tree;
using namespace mlpack::data; int main()
{ // 加载数据集(假设数据集是CSV格式,且最后一列是标签) arma::mat data; arma::Row<size_t> labels; Load("dataset.csv", data, true); // 假设数据集文件名为dataset.csv labels = data.row(data.n_rows - 1); data.shed_row(data.n_rows - 1); // 划分训练集和测试集(这里简化为只使用前80%作为训练集) size_t trainSize = data.n_cols * 0.8; arma::mat trainData = data(:, arma::span(0, trainSize - 1)); arma::Row<size_t> trainLabels = labels(arma::span(0, trainSize - 1)); // 创建并训练决策树模型 const size_t numClasses = 3; // 假设是3分类问题 const size_t minimumLeafSize = 10; DecisionTree<> dt(trainData, trainLabels, numClasses, minimumLeafSize); // 使用训练好的模型进行预测(这里简化为对训练集自身进行预测) arma::Row<size_t> predictions; dt.Classify(trainData, predictions); // 计算准确率等性能指标... // ... return 0;
}请注意,C++示例代码是一个高度简化的模板,用于说明如何在C++中使用决策树。在实际应用中,数据集的加载、预处理、模型评估和性能度量等步骤可能更加复杂。另外,mlpack库可能需要单独安装和配置。如果你打算在生产环境中使用C++实现决策树,可能需要考虑更多细节和异常处理。
如果你希望完全从底层实现决策树算法,那么你需要手动编写代码来处理决策树的构建、特征选择、树的遍历以及剪枝等操作,这通常需要对算法和数据结构有深入的理解。
4.4. 支持向量机(Support Vector Machine, SVM)
- 基础概念:支持向量机是一种二分类和多分类的监督学习算法,通过构建超平面或超曲面来实现分类。
- 算法示例:图像识别。在图像处理领域,SVM 可以用于识别手写数字、人脸识别等任务。
支持向量机(Support Vector Machine, SVM)是一种非常流行的监督学习算法,主要用于分类和回归分析。SVM 的主要思想是在高维空间中寻找一个最优超平面,这个超平面能够将不同类别的数据点分隔开,并且使得两侧距离超平面最近的点(即支持向量)到超平面的间隔最大化。
4.4.1. SVM 的主要概念
-
支持向量:是数据集中距离决策边界(超平面)最近的点,这些点对确定决策边界起到了关键作用。
-
间隔(Margin):是指支持向量到决策边界的距离,SVM 的目标是最大化这个间隔。
-
核函数:当数据不是线性可分的时候,可以通过核函数将数据映射到更高维的空间,使其在新的空间中线性可分。
-
软间隔与硬间隔:硬间隔是指所有数据点都必须严格分类正确,不允许有错误分类;而软间隔则允许一些数据点被错误分类,通过引入惩罚项来控制错误分类的程度。
4.4.2. SVM 的优点
- 在高维空间中表现良好。
- 只使用部分训练数据(支持向量)来做决策,使得模型更加高效。
- 可以使用不同的核函数来处理非线性问题。
4.4.3. 算法示例
Python 算法示例
在 Python 中,通常使用 scikit-learn 库来应用 SVM 算法。
from sklearn import svm
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score # 加载数据集
iris = load_iris()
X = iris.data
y = iris.target # 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 创建 SVM 分类器
clf = svm.SVC(kernel='linear', C=1.0, random_state=42) # 训练模型
clf.fit(X_train, y_train) # 预测测试集
y_pred = clf.predict(X_test) # 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy}")C++ 算法示例
在 C++ 中,可以使用一些机器学习库,如 mlpack 或 OpenCV,来实现 SVM。以下是一个使用 OpenCVOpenCV - Open Computer Vision Library 的 SVM 示例:
#include <opencv2/opencv.hpp>
#include <opencv2/ml/ml.hpp>
#include <iostream> int main() { // 加载数据(这里只是一个示例,实际数据需要自行准备) cv::Mat_<float> trainingData(4, 2); // 4个样本,每个样本2个特征 cv::Mat_<int> labels(4, 1); // 4个标签 // 填充数据和标签(仅为示例) trainingData << 501, 10, 255, 10, 501, 255, 10, 501; labels << 1, -1, -1, 1; // 创建 SVM 对象 cv::Ptr<cv::ml::SVM> svm = cv::ml::SVM::create(); svm->setType(cv::ml::SVM::C_SVC); svm->setC(0.1); svm->setKernel(cv::ml::SVM::LINEAR); svm->setTermCriteria(cv::TermCriteria(cv::TermCriteria::MAX_ITER, 100, 1e-6)); // 训练 SVM svm->train(trainingData, cv::ml::ROW_SAMPLE, labels); // 预测 cv::Mat_<float> sample(1, 2); sample << 400, 150; // 测试样本 float response = svm->predict(sample)[0]; std::cout << "Prediction for sample [" << sample << "] is: " << response << std::endl; return 0;
}在这个 C++ 示例中,我们使用了 OpenCV 库来创建和训练一个 SVM 模型。需要注意的是,OpenCV 中的 SVM 实现与 scikit-learn 略有不同,特别是在参数设置和接口方面。你需要根据你的具体数据和任务来调整这些参数。
在使用这些代码之前,请确保你已经正确安装了所需的库(如 scikit-learn 或 OpenCV),并根据你的环境和数据集调整代码。
4.5. 朴素贝叶斯(Naive Bayes)
- 基础概念:朴素贝叶斯算法是基于贝叶斯定理和特征条件独立性假设的分类算法。
- 算法示例:垃圾邮件过滤。通过分析邮件内容中的关键词,使用朴素贝叶斯模型来判断一封邮件是否为垃圾邮件。
4.5.1. 算法介绍
朴素贝叶斯算法基于以下两个核心思想:
贝叶斯定理:用于计算后验概率,即在已知某些特征的情况下,样本属于某个类别的概率。
特征条件独立假设:朴素贝叶斯假设各个特征之间相互独立,这是算法“朴素”之名的由来。尽管这个假设在实际应用中往往不成立,但朴素贝叶斯算法在很多情况下仍然表现良好。
算法步骤如下:
数据准备:准备训练数据集,包括特征和对应的类别标签。
计算先验概率:计算每个类别在训练数据中出现的概率。
计算条件概率:对于每个特征,计算它在每个类别中出现的概率。
应用贝叶斯定理:对于新的数据样本,使用贝叶斯定理和前面计算得到的先验概率及条件概率,计算该样本属于每个类别的后验概率。
分类决策:将样本分类到后验概率最大的类别中。
4.5.2. 算法示例
Python算法示例
在Python中,可以使用scikit-learn库中的GaussianNB(适用于连续特征)或MultinomialNB(适用于离散特征)等实现朴素贝叶斯分类器。以下是一个使用GaussianNB的示例:
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score # 加载数据集
iris = load_iris()
X, y = iris.data, iris.target # 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 创建并训练朴素贝叶斯分类器
gnb = GaussianNB()
gnb.fit(X_train, y_train) # 预测测试集并计算准确率
y_pred = gnb.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy}")C++算法示例
在C++中实现朴素贝叶斯算法通常需要手动编写更多的代码,因为C++标准库没有直接提供机器学习算法。以下是一个简化的朴素贝叶斯分类器的C++示例,仅用于说明基本概念:
#include <iostream>
#include <vector>
#include <map> // 假设特征只有一维,且为离散值
struct DataPoint { int feature; int label;
}; class NaiveBayesClassifier {
private: std::map<int, int> classCounts; // 类别计数 std::map<int, std::map<int, int>> featureCounts; // 特征在每个类别的计数 std::map<int, int> totalFeatureCounts; // 每个类别的总特征计数 public: void train(const std::vector<DataPoint>& data) { for (const auto& point : data) { // 更新类别计数 classCounts[point.label]++; // 更新特征计数 featureCounts[point.label][point.feature]++; // 更新每个类别的总特征计数 totalFeatureCounts[point.label]++; } } int predict(int feature) { int bestClass = -1; double maxProbability = 0.0; for (const auto& classCount : classCounts) { int classLabel = classCount.first; int classTotalCount = classCount.second; int featureCountInClass = featureCounts[classLabel][feature]; double probability = static_cast<double>(featureCountInClass + 1) / (totalFeatureCounts[classLabel] + 2); // 使用拉普拉斯平滑 if (probability > maxProbability) { maxProbability = probability; bestClass = classLabel; } } return bestClass; }
}; int main() { NaiveBayesClassifier classifier; std::vector<DataPoint> trainingData = { {1, 0}, {2, 0}, {1, 1}, {2, 1}, {3, 1}, {2, 0} }; classifier.train(trainingData); int prediction = classifier.predict(2); std::cout << "Predicted class for feature 2: " << prediction << std::endl; return 0;
}请注意,这个C++示例非常简化,仅用于教学目的。在实际应用中,朴素贝叶斯分类器可能需要处理多维特征和连续特征,这会增加实现的复杂性。此外,为了提高性能和准确性,可能还需要进行特征选择、特征转换和模型评估等步骤。
4.6. k-近邻算法(K-Nearest Neighbors, KNN)
- 基础概念:KNN 是一种基于实例的学习算法,通过计算新数据与训练数据集中数据点之间的距离来找到最近的 k 个邻居,并根据这些邻居的类别来确定新数据的类别。
- 算法示例:手写数字识别。可以使用 KNN 算法来识别手写数字图像。
4.6.1. k-近邻算法介绍
k-近邻算法(k-Nearest Neighbors,简称k-NN)是一种基于实例的学习算法,它的基本思想是通过测量不同数据点之间的距离进行分类。在k-NN中,一个对象的分类是由其邻居的“多数表决”确定的,k个最近邻居(k为正整数,通常较小)中最常见的分类决定了赋予该对象的类别。若k=1,则该对象的类别直接由最近的一个节点赋予。
4.6.2. k-近邻算法步骤
- 计算距离:对于未知分类的数据,计算它到每个已知分类数据之间的距离。
- 寻找邻居:按照距离的递增关系进行排序,然后选择距离最小的k个点。
- 确定类别:确定前k个点所在类别的出现频率,返回前k个点出现频率最高的类别作为预测分类。
4.6.3. 算法示例
Python算法示例
在Python中,我们可以使用scikit-learn库中的KNeighborsClassifier来实现k-NN算法。以下是一个简单的示例:
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score # 加载iris数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target # 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test) # 创建k-NN分类器,并设置邻居数为3
knn = KNeighborsClassifier(n_neighbors=3) # 训练模型
knn.fit(X_train, y_train) # 预测测试集
y_pred = knn.predict(X_test) # 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy}")C++算法示例
在C++中实现k-NN算法需要手动编写距离计算、排序和分类的逻辑。以下是一个简化的k-NN分类器的C++示例:
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
#include <limits> struct Point { std::vector<double> features; int label;
}; double euclideanDistance(const std::vector<double>& a, const std::vector<double>& b) { double sum = 0.0; for (size_t i = 0; i < a.size(); ++i) { sum += pow(a[i] - b[i], 2); } return sqrt(sum);
} int kNearestNeighbors(const std::vector<Point>& dataset, const std::vector<double>& point, int k) { std::vector<std::pair<double, int>> distances; // 存储距离和对应的标签索引 for (size_t i = 0; i < dataset.size(); ++i) { double dist = euclideanDistance(dataset[i].features, point); distances.push_back(std::make_pair(dist, i)); } // 按距离排序 std::sort(distances.begin(), distances.end()); // 统计k个最近邻居的标签 std::map<int, int> labelCounts; for (int i = 0; i < k; ++i) { int label = dataset[distances[i].second].label; labelCounts[label]++; } // 找到出现次数最多的标签 int maxCount = 0; int majorityLabel = -1; for (const auto& entry : labelCounts) { if (entry.second > maxCount) { maxCount = entry.second; majorityLabel = entry.first; } } return majorityLabel;
} int main() { std::vector<Point> dataset = { {{1, 2}, 1}, {{1, 4}, 1}, {{3, 4}, 2}, {{4, 2}, 2}, {{2, 3}, 1} }; std::vector<double> queryPoint = {2, 2}; int k = 3; // 设置k值 int predictedLabel = kNearestNeighbors(dataset, queryPoint, k); std::cout << "Predicted label for point (" << queryPoint[0] << ", " << queryPoint[1] << "): " << predictedLabel << std::endl; return 0;
}这个C++示例中,我们定义了一个Point结构体来存储数据点的特征和标签。euclideanDistance函数用于计算两个点之间的欧几里得距离。kNearestNeighbors函数实现了k-NN算法的核心逻辑,包括计算距离、排序、统计标签和确定多数类别。在main函数中,我们创建了一个简单的数据集,并设置了一个查询点和k值来演示算法的使用。
4.7. k-平均算法(K-Means)
- 基础概念:K-Means 是一种无监督学习算法,用于将数据集中的样本划分为 k 个类别或簇。
- 算法示例:市场细分。通过分析消费者的购买行为等数据,使用 K-Means 算法将消费者划分为不同的群体,以便制定更精准的营销策略。算法可以运用于游戏中游戏世界内商城控制、交易类金额控制,但真的不建议做在真银子换游戏币中,会有被惩罚的可能性哦
4.7.1. k-平均算法介绍
k-平均算法(k-means clustering)是一种非常流行的无监督学习算法,用于将数据点划分为K个集群。该算法的目标是使得每个数据点与其所属集群的中心点之间的距离之和最小。
4.7.2. k-平均算法步骤
- 初始化:选择K个点作为初始集群中心(这些点可以是数据集中的随机点)。
- 分配数据点到最近的集群中心:对于数据集中的每个点,计算它到每个集群中心的距离,并将其分配给最近的集群。
- 重新计算集群中心:对于每个集群,计算所有数据点的平均值,并将这个平均值设为新的集群中心。
- 迭代:重复步骤2和3,直到集群中心不再发生显著变化,或者达到预定的迭代次数。
4.7.3. 算法示例
Python算法示例
在Python中,我们可以使用scikit-learn库中的KMeans类来实现k-means算法。以下是一个简单的示例:
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt # 生成模拟数据
X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0) # 创建KMeans实例,并设置集群数量为4
kmeans = KMeans(n_clusters=4) # 训练模型
kmeans.fit(X) # 预测集群标签
labels = kmeans.predict(X) # 绘制结果
plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='red', marker='x')
plt.show()C++算法示例
在C++中实现k-means算法需要手动编写距离计算、集群中心更新和数据点分配的逻辑。以下是一个简化的k-means算法的C++示例:
#include <iostream>
#include <vector>
#include <cmath>
#include <limits>
#include <ctime>
#include <cstdlib> struct Point { double x, y; int cluster;
}; double distance(const Point& a, const Point& b) { return std::sqrt(std::pow(a.x - b.x, 2) + std::pow(a.y - b.y, 2));
} void kMeansClustering(std::vector<Point>& data, int K, int maxIterations) { srand(time(0)); // 使用当前时间作为随机数生成器的种子 // 初始化集群中心 std::vector<Point> centers(K); for (int i = 0; i < K; ++i) { centers[i] = data[rand() % data.size()]; // 随机选择数据点作为初始中心 centers[i].cluster = i; // 设置集群标签 } bool changed; int iteration = 0; do { changed = false; // 分配数据点到最近的集群中心 for (auto& point : data) { double minDist = std::numeric_limits<double>::max(); int closestCenter = -1; for (int i = 0; i < K; ++i) { double dist = distance(point, centers[i]); if (dist < minDist) { minDist = dist; closestCenter = i; } } if (point.cluster != closestCenter) { point.cluster = closestCenter; changed = true; } } // 重新计算集群中心 if (changed || iteration == 0) { for (int i = 0; i < K; ++i) { double sumX = 0, sumY = 0; int count = 0; for (const auto& point : data) { if (point.cluster == i) { sumX += point.x; sumY += point.y; count++; } } if (count > 0) { centers[i].x = sumX / count; centers[i].y = sumY / count; } } } iteration++; } while (changed && iteration < maxIterations);
} int main() { // 示例数据点(在实际应用中,这些数据通常是从文件或数据库中读取的) std::vector<Point> data = { /* 填充数据点 */ }; const int K = 3; // 集群数量 const int maxIterations = 100; // 最大迭代次数 kMeansClustering(data, K, maxIterations); // 输出集群结果或进行其他后续处理... return 0;
}注意:上述C++示例代码是一个框架性的实现,你需要填充实际的数据点以及可能的其他逻辑来完成k-means算法的实现。在实际应用中,通常还需要添加更多的错误处理和优化。
4.8. 庆祝下
看到这里的小伙伴是壮士,写这些我自己也头秃,下一步加油,这只是刚开始哦~~~~

相关文章:

游戏AI的创造思路-技术基础-机器学习(2)
本篇存在大量的公式,数学不好的孩子们要开始恶补数学了,尤其是统计学和回归方程类的内容。 小伙伴们量力而行~~~~~ 游戏呢,其实最早就是数学家、元祖程序员编写的数学游戏,一脉相承传承至今,囊括了更多的设计师、美术…...

【深度学习】记录为什么没有调用GPU
排查CLIP为什么评测推理没有调用GPU,主要是这个代码:https://github.com/OFA-Sys/Chinese-CLIP/blob/master/cn_clip/eval/extract_features.py 第一次认为:因为model并没有to.cuda()。 但是又发现,model.cuda(args.gpu) # 已经加…...

vite 创建vue3项目 集成 ESLint、Prettier、Sass等
在网上找了一大堆vue3脚手架的东西,无非就是vite或者vue-cli,在vue2时代,vue-cli用的人挺多的,也很好用,然而vue3大多是和vite搭配搭建的,而且个人感觉vite这个脚手架并没有那么的好用,搭建项目时只能做两个…...

计算机系统基础知识(上)
目录 计算机系统的概述 计算机的硬件 处理器 存储器 总线 接口 外部设备 计算机的软件 操作系统 数据库 文件系统 计算机系统的概述 如图所示计算机系统分为软件和硬件:硬件包括:输入输出设备、存储器,处理器 软件则包括系统软件和…...

[深度学习]循环神经网络RNN
RNN(Recurrent Neural Network,即循环神经网络)是一类用于处理序列数据的神经网络,广泛应用于自然语言处理(NLP)、时间序列预测、语音识别等领域。与传统的前馈神经网络不同,RNN具有循环结构&am…...

【C++:list】
list概念 list是一个带头的双向循环链表,双向循环链表的特色:每一个节点拥有两 个指针进行维护,俩指针分别为prev和next,prev指该节点的前一个节点,next为该节点的后一个节点 list的底层实现中为什么对迭代器单独写一个结构体进行…...

解锁 Apple M1/M2 上的深度学习力量:安装 TensorFlow 完全指南
前言 随着 Apple M1 和 M2 芯片的问世,苹果重新定义了笔记本电脑和台式机的性能标准。这些强大的芯片不仅适用于日常任务,还能处理复杂的机器学习和深度学习工作负载。本文将详细介绍如何在 Apple M1 或 M2 芯片上安装和配置 TensorFlow,助你…...

Apache Iceberg:现代数据湖存储格式的未来
Apache Iceberg 是一个开源的表格式,用于在分布式数据湖中管理大规模数据集。它由 Netflix 开发,并捐赠给 Apache 基金会。Iceberg 的设计目标是解决传统数据湖存储格式(如 Apache Hive 和 Apache Parquet)在大规模数据管理中的一…...

【离散数学·图论】(复习)
一、基本概念 1.一些基本术语: 2.点u,v邻接(或相邻): 边e称为关联顶点u和v,or e连接u和v; 3.G(V,E)中,顶点v所有邻居的集合:N(v), 成为v的邻域。 4.度 : deg(v) 5.悬挂点:度为1的…...

【ONLYOFFICE震撼8.1】ONLYOFFICE8.1版本桌面编辑器测评
随着远程工作的普及和数字化办公的发展,越来越多的人开始寻找一款具有强大功能和便捷使用的办公软件。在这个时候,ONLYOFFICE 8.1应运而生,成为了许多用户的新选择。ONLYOFFICE 8.1是一种办公套件软件,它提供了文档处理、电子表格…...

Shell 脚本编程保姆级教程(上)
一、运行第一个 Shell 脚本 1.1 Shell 脚本 Shell 脚本(shell script),是一种为 shell 编写的脚本程序。 业界所说的 shell 通常都是指 shell 脚本,但读者朋友要知道,shell 和 shell script 是两个不同的概念。 由…...

凸优化相关文章汇总
深度学习/机器学习入门基础数学知识整理(三):凸优化,Hessian,牛顿法_深度学习和凸优化-CSDN博客 深度学习/机器学习入门基础数学知识整理(四):拟牛顿法、BFGS、L-BFGS、DFP、共轭梯…...
Java鲜花下单预约系统源码小程序源码
让美好触手可及 🌸一、开启鲜花新篇章 在繁忙的都市生活中,我们总是渴望那一抹清新与美好。鲜花,作为大自然的馈赠,总能给我们带来无尽的惊喜与愉悦。但你是否曾因为工作繁忙、时间紧张而错过了亲自挑选鲜花的机会?今…...

网络变压器和RJ45接线的方法
网络变压器在以太网硬件电路设计中扮演着重要的角色,它主要用于信号电平耦合、隔离外部干扰、实现阻抗匹配以及增加传输距离。而RJ45接口则是以太网连接的标准化接口,它提供了与网络电缆的连接点。 网络变压器与RJ45的接线方法通常遵循以下步骤…...

Matlab/simulink三段式电流保护
电流1段仿真波形如下所示 电流2段仿真波形如下所示 电流3段仿真波形如下所示...

OOXML入门学习
进入-飞入 <par> <!-- 这是一个并行动画序列的开始。"par"代表并行,意味着在这个标签内的所有动画将同时开始。 --><cTn id"5" presetID"2" presetClass"entr" presetSubtype"4" fill"hold&…...

k8s集群node节点加入失败
出现这种情况: [preflight] FYI: You can look at this config file with kubectl -n kube-system get cm kubeadm-config -o yaml [kubelet-start] Writing kubelet configuration to file "/var/lib/kubelet/config.yaml" [kubelet-start] Writing kub…...

layui+jsp项目中实现table单元格嵌入下拉选择框功能,下拉选择框可手动输入内容或选择默认值,修改后数据正常回显。
需求 table列表中的数据实现下拉框修改数据,当默认的下拉框不符合要求时,可手动输入内容保存。内容修改后表格显示修改后的值同时表格不刷新。 实现 layui框架下拉框组件只能选择存在的数据,不支持将输入的内容显示在input中的功能&#x…...

2024年客户体验的几个预测
数字化转型、以客户为中心的理念、数字技术的发展和产品的不断创新,都为客户体验带来了巨大的改变。 目前,我们看到很多公司都在致力于塑造一种以客户为中心的商业模式。企业开始用更多技术、更多数据和更多产品来强化自己在客户体验方面的能力。 那么&a…...
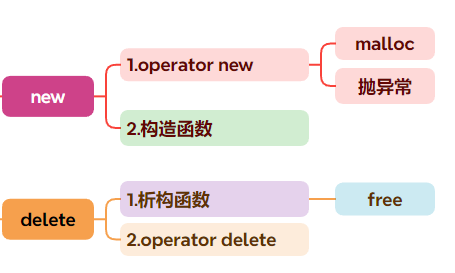
【C++】动态内存管理new和delete
文章目录 一、C的内存管理方式二、new和delete的用法1.操作内置类型2.操作自定义内置类型 三、new和delete的底层实现1.operator new和operator delete函数2.new和delete的实现原理 四、定位new表达式五、malloc/free和new/delete的区别 一、C的内存管理方式 之前在C语言的动态…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...

【阅读笔记】MemOS: 大语言模型内存增强生成操作系统
核心速览 研究背景 研究问题:这篇文章要解决的问题是当前大型语言模型(LLMs)在处理内存方面的局限性。LLMs虽然在语言感知和生成方面表现出色,但缺乏统一的、结构化的内存架构。现有的方法如检索增强生成(RA…...

【Vue】scoped+组件通信+props校验
【scoped作用及原理】 【作用】 默认写在组件中style的样式会全局生效, 因此很容易造成多个组件之间的样式冲突问题 故而可以给组件加上scoped 属性, 令样式只作用于当前组件的标签 作用:防止不同vue组件样式污染 【原理】 给组件加上scoped 属性后…...
