信息学奥赛初赛天天练-38-CSP-J2021阅读程序-约数个数、约数和、埃氏筛法、欧拉筛法筛素数应用
PDF文档公众号回复关键字:20240628

2021 CSP-J 阅读程序3
1阅读程序(判断题1.5分 选择题3分 共计40分 )
01 #include<stdio.h>
02 using namespace std;
03
04 #define n 100000
05 #define N n+1
06
07 int m;
08 int a[N],b[N],c[N],d[N];
09 int f[N],g[N];
10
11 void init()
12 {
13 f[1]=g[1]=1;
14 for(int i=2;i<=n;i++){
15 if(!a[i]){
16 b[m++]=i;
17 c[i]=1,f[i]=2;
18 d[i]=1,g[i]=i+1;
19 }
20 for(int j=0;j<m&&b[j]*i<=n;j++){
21 int k=b[j];
22 a[i*k]=1;
23 if(i%k==0){
24 c[i*k]=c[i]+1;
25 f[i*k]=f[i]/c[i*k]*(c[i*k]+1);
26 d[i*k]=d[i];
27 g[i*k]=g[i]*k+d[i];
28 break;
29 }
30 else{
31 c[i*k]=1;
32 f[i*k]=2*f[i];
33 d[i*k]=g[i];
34 g[i*k]=g[i]*(k+1);
35 }
36 }
37 }
38 }
39
40 int main()
41 {
42 init();
43
44 int x;
45 scanf("%d",&x);
46 printf("%d %d\n",f[x],g[x]);
47 return 0;
48 }
假设输入的x是不超过1000的自然数,完成下面的判断题和单选题
判断题
28.若输入不为"1",把第13删去不会影响输出的结果( )
29.(2分) 第25行的"f[i]/c[i*k]"可能存在的无法整除而向下取取整的情况( )
30.(2分)在执行完init()后,f数组不是单调递增的,但g数组是单调递增的( )
单选题
31.init 函数的时间复杂度为( )
A. O(n)
B. O(nlogn)
C. O(n sqrt(n))
D. O(n^2)
32.在执行完init()后,f[1],f[2],f[3]… f[100]中有( )个等于2.
A. 23
B. 24
C. 25
D. 26
33.(4分)当输入为"1000"时,输出为( )
A. “15 1340”
B. “15 2340”
C. “16 2340”
D. “16 1340”
2 相关知识点
埃式筛法
如果一个数是素数,那么它的倍数一定不是素数。我们要找n以内的所有素数,那么把n以内的合数全部筛掉,剩下的就是素数了
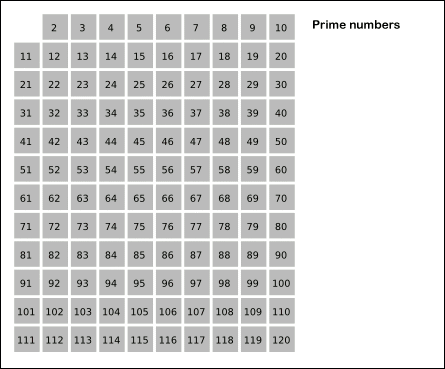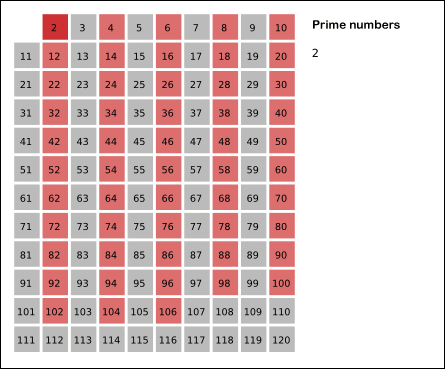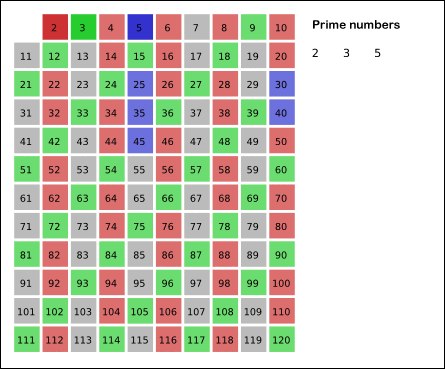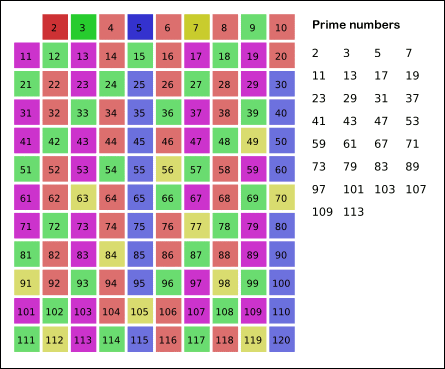
时间复杂度
O(n * log (log n) )
欧拉筛法
将合数分解为一个最小质数乘以另一个数的形式,即 合数 = 最小质数 * 自然数,然后通过最小质数来判断当前数是否被标记过
时间复杂度
O(n)
3 思路分析
分析
本程序通过欧拉筛求约数个数及其约数和
使用到的对应数组
标记a数组,对合数进行标记,未标记的则是质数
质数表b数组,从小到大知道质数写到b数组
约数个数f数组,记录一个数对应的约数的个数
在填入约数个数f数组时,使用到最小质因数个数c数组
在填入约数和g数组时,使用到约数和对应的连乘积除第1项外的其他连乘积d数组
约数和g数组,记录一个数对应的约数之和
08 int a[N],b[N],c[N],d[N];
09 int f[N],g[N];
假设输入的x是不超过1000的自然数,完成下面的判断题和单选题
判断题
28.若输入不为"1",把第13删去不会影响输出的结果( T )
分析
13行程序计算并未使用,只对f[1],g[1]输出有影响,如果不输出f[1],g[1],不会影响输出
所以输入不为"1",删除不影响输出结果
29.(2分) 第25行的"f[i]/c[i*k]"可能存在的无法整除而向下取取整的情况( F )
分析
c[i]表示i的最小质因数个数
f[i]表示i的约数个数,计算公式如下H = p1^a1 * p2^a2 ....pn^an 其中 pi都是质数,ai是幂次,p1是最小的质数
约数的个数f[i]=(a1+1)*(a2+1)*...(an+1)
其中a1是最小质因数个数
c[i]表示i的最小质因数个数=a1
满足条件i%k==0
c[i*k]=相当于最小质数+1=a1+1
a1+1是f[i]的因子,所以f[i]/c[i*k]不会存在无法整除的情况
所以错误
30.(2分)在执行完init()后,f数组不是单调递增的,但g数组是单调递增的( F )
分析
f数组是约数个数,合数个数多,质数个数少,3 4 5 对应约数个数分别是2 3 2 看,并不是单调递增的
g数组是约数和,3 4 5 对应约数和分别是4 7 6 看,并不是单调递增的
单选题
31.init 函数的时间复杂度为( A )
A. O(n)
B. O(nlogn)
C. O(n sqrt(n))
D. O(n^2)
分析
此算法是欧拉筛法求质数,欧拉筛是线性筛法,即所有的合数都被它最小的质因子筛一次,减少了埃氏筛法的重复筛的次数,时间复杂度近似O(n)
32.在执行完init()后,f[1],f[2],f[3]… f[100]中有( C )个等于2.
A. 23
B. 24
C. 25
D. 26
分析
f数组是约数个数,约数个数和为2,表示对应数组下标的数为质数
1~100之间的质数有25个,分别是
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97
33.(4分)当输入为"1000"时,输出为( C )
A. “15 1340”
B. “15 2340”
C. “16 2340”
D. “16 1340”
分析
由程序逻辑知分别输出1000对应的约数个数及其对应的约数和
1000=2^3 * 5^3第1项求约数个数,根据约数个数公式
(3+1)*(3+1)=16
第2项求约数和,根据约数和公式
(2^0+2^1+2^2+2^3) * (5^0+5^1+5^2+5^3)=2340
所以选C
相关文章:

信息学奥赛初赛天天练-38-CSP-J2021阅读程序-约数个数、约数和、埃氏筛法、欧拉筛法筛素数应用
PDF文档公众号回复关键字:20240628 2021 CSP-J 阅读程序3 1阅读程序(判断题1.5分 选择题3分 共计40分 ) 01 #include<stdio.h> 02 using namespace std; 03 04 #define n 100000 05 #define N n1 06 07 int m; 08 int a[N],b[N],c[N],d[N]; 09 int f[N],g[N]; 10 11 …...
第100+13步 ChatGPT学习:R实现决策树分类
基于R 4.2.2版本演示 一、写在前面 有不少大佬问做机器学习分类能不能用R语言,不想学Python咯。 答曰:可!用GPT或者Kimi转一下就得了呗。 加上最近也没啥内容写了,就帮各位搬运一下吧。 二、R代码实现决策树分类 (…...

Hi3861 OpenHarmony嵌入式应用入门--LiteOS MessageQueue
CMSIS 2.0接口中的消息(Message)功能主要涉及到实时操作系统(RTOS)中的线程间通信。在CMSIS 2.0标准中,消息通常是通过消息队列(MessageQueue)来进行处理的,以实现不同线程之间的信息…...

ffmpeg编码图象时报错Invalid buffer size, packet size * < expected frame_size *
使用ffmpeg将单个yuv文件编码转为jpg或其他图像格式时,报错: Truncating packet of size 11985408 to 3585 [rawvideo 0x1bd5390] Packet corrupt (stream 0, dts 1). image_3264_2448_0.yuv: corrupt input packet in stream 0 [rawvideo 0x1bd7c60…...

解决类重复的问题
1.针对AndroidX 类重复问题 解决办法: android.useAndroidXtrue android.enableJetifiertrue2.引用其他sdk出现类重复的问题解决办法:configurations {all { // You should exclude one of them not both of themexclude group: "com.enmoli"…...

使用 shell 脚本 统计app冷启动耗时
下面是一个 shell 脚本,它使用 参数将包名称作为参数--app,识别相应应用程序进程的 PID,使用 终止该进程adb shell kill,最后使用 重新启动该应用程序adb shell am start: #!/bin/bash# Check if package name is pro…...
使用容器部署redis_设置配置文件映射到本地_设置存储数据映射到本地_并开发java应用_连接redis---分布式云原生部署架构搭建011
可以看到java应用的部署过程,首先我们要准备一个java应用,并且我们,用docker,安装一个redis 首先我们去start.spring.io 去生成一个简单的web项目,然后用idea打开 选择以后下载 放在这里,然后我们去安装redis 在公共仓库中找到redis . 可以看到它里面介绍说把数据放到了/dat…...

第五节:如何使用其他注解方式从IOC中获取bean(自学Spring boot 3.x的第一天)
大家好,我是网创有方,上节我们实践了通过Bean方式声明Bean配置。咱们这节通过Component和ComponentScan方式实现一个同样功能。这节实现的效果是从IOC中加载Bean对象,并且将Bean的属性打印到控制台。 第一步:创建pojo实体类studen…...

Paragon NTFS与Tuxera NTFS有何区别 Mac NTFS 磁盘读写工具选哪个好
macOS系统虽然以稳定、安全系数高等优点著称,但因其封闭性,不能对NTFS格式磁盘写入数据常被人们诟病。优质的解决方案是使用磁盘管理软件Paragon NTFS for Mac(点击获取激活码)和Tuxera NTFS(点击获取激活码࿰…...

EtherCAT主站IGH-- 2 -- IGH之coe_emerg_ring.h/c文件解析
EtherCAT主站IGH-- 2 -- IGH之coe_emerg_ring.h/c文件解析 0 预览一 该文件功能coe_emerg_ring.c 文件功能函数预览 二 函数功能介绍coe_emerg_ring.c 中主要函数的作用1. ec_coe_emerg_ring_init2. ec_coe_emerg_ring_clear3. ec_coe_emerg_ring_size4. ec_coe_emerg_ring_pus…...

psensor 的手势功能
psensor 的手势功能的移植过程 有时间再来写下...
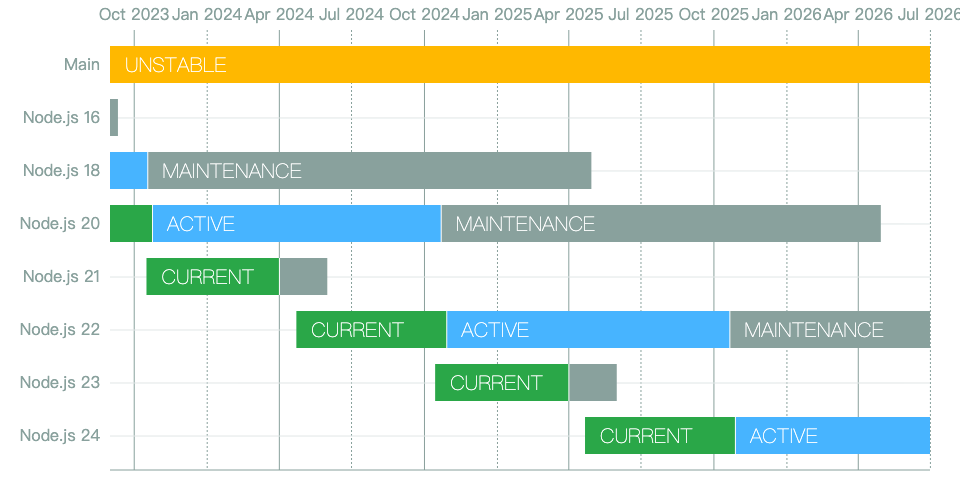
使用 nvm 管理 Node 版本及 pnpm 安装
文章目录 GithubWindows 环境Mac/Linux 使用脚本进行安装或更新Mac/Linux 环境变量nvm 常用命令npm 常用命令npm 安装 pnpmNode 历史版本 Github https://github.com/nvm-sh/nvm Windows 环境 https://nvm.uihtm.com/nvm.html Mac/Linux 使用脚本进行安装或更新 curl -o- …...
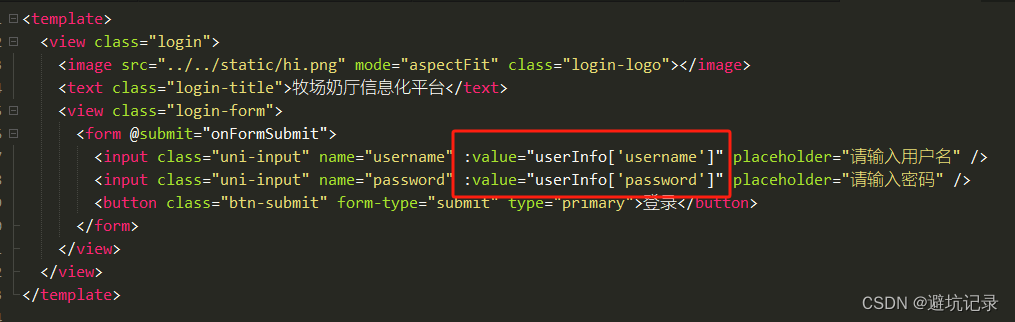
uni-appx使用form表单页面初始化报错
因为UniFormSubmitEvent的类型时 e-->detail-->value,然后没有了具体值。所以页面初始化的时候 不能直接从value取值,会报错找不到 所以form表单里的数据我们要设置成一个对象来存放 这个问题的关键在于第22行代码 取值: 不能按照点的方式取值 …...

TiDB-从0到1-数据导出导入
TiDB从0到1系列 TiDB-从0到1-体系结构TiDB-从0到1-分布式存储TiDB-从0到1-分布式事务TiDB-从0到1-MVCCTiDB-从0到1-部署篇TiDB-从0到1-配置篇TiDB-从0到1-集群扩缩容 一、数据导出 TiDB中通过Dumpling来实现数据导出,与MySQL中的mysqldump类似,其属于…...
代码实践 -卷积神经网络-16自定义层)
动手学深度学习(Pytorch版)代码实践 -卷积神经网络-16自定义层
16自定义层 import torch import torch.nn.functional as F from torch import nnclass CenteredLayer(nn.Module):def __init__(self):super().__init__()#从其输入中减去均值#X.mean() 计算的是整个张量的均值#希望计算特定维度上的均值,可以传递 dim 参数。#例如…...

树莓派4设置
使用sudo命令时要求输入密码 以 sudo 为前缀的命令以超级用户身份运行。默认情况下,超级用户不需要密码。不过,您可以要求所有以 sudo 运行的命令都输入密码,从而提高 Raspberry Pi 的安全性。 要强制 sudo 要求输入密码,请为你…...

44.商城系统(二十五):k8s基本操作,ingress域名访问,kubeSphere可视化安装
上一章我们已经配置好了k8s集群,如果没有配置好先去照着上面的配。 一、k8s入门操作 1.部署一个tomcat,测试容灾恢复 #在主机器上执行 kubectl create deployment tomcat6 --image=tomcat:6.0.53-jre8#查看k8s中的所有资源 kubectl get all kubectl get all -o wide#查看po…...

MySQL高级查询
MySQL 前言 文本源自微博客 (www.microblog.store),且已获授权. 一. mysql基础知识 1. mysql常用系统命令 启动命令 net start mysql停止命令 net stop mysql登录命令 mysql -h ip -P 端口 -u 用户名 -p 本机可以省略 ip mysql -u 用户名 -p 查看数据库版本 mysql --ve…...

聊聊啥项目适合做自动化测试
作为测试从业者,你是否遇到过这样的场景,某天公司大Boss找你谈话。 老板:小李,最近工作辛苦了 小李:常感谢您的认可,这不仅是对我个人的鼓励,更是对我们整个团队努力的认可。我们的成果离不开每…...

ROS2开发机器人移动
.创建功能包和节点 这里我们设计两个节点 example_interfaces_robot_01,机器人节点,对外提供控制机器人移动服务并发布机器人的状态。 example_interfaces_control_01,控制节点,发送机器人移动请求,订阅机器人状态话题…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...

Qwen系列之Qwen3解读:最强开源模型的细节拆解
文章目录 1.1分钟快览2.模型架构2.1.Dense模型2.2.MoE模型 3.预训练阶段3.1.数据3.2.训练3.3.评估 4.后训练阶段S1: 长链思维冷启动S2: 推理强化学习S3: 思考模式融合S4: 通用强化学习 5.全家桶中的小模型训练评估评估数据集评估细节评估效果弱智评估和民间Arena 分析展望 如果…...

大模型真的像人一样“思考”和“理解”吗?
Yann LeCun 新研究的核心探讨:大语言模型(LLM)的“理解”和“思考”方式与人类认知的根本差异。 核心问题:大模型真的像人一样“思考”和“理解”吗? 人类的思考方式: 你的大脑是个超级整理师。面对海量信…...

Axure Rp 11 安装、汉化、授权
Axure Rp 11 安装、汉化、授权 1、前言2、汉化2.1、汉化文件下载2.2、windows汉化流程2.3、 macOs汉化流程 3、授权 1、前言 Axure Rp 11官方下载链接:https://www.axure.com/downloadthanks 2、汉化 2.1、汉化文件下载 链接: https://pan.baidu.com/s/18Clf…...
