01背包问题(大彻大悟版)
背包问题身为一个非常经典的动态规划问题,理清思路很重要,在经过多次观看y总视频和b站解析,加上CSDN的文章辅助,我终于从很多不理解到大彻大悟,下面是我对于背包问题思路的总结,有问题的话欢迎指出。
谈到背包问题,先以下面这最经典的一道背包问题为例子
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 ii 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5输出样例:
8不废话,直接给出两种思路(可以结合看)
bilibili表格法
b站中把背包问题转化为一个表格来理解,我觉得特别有用,对于背包问题光是靠说是很难理解的,通过表格总结公式和方法,对于该题非常有效,入门背包问题必须要看看。(链接:【【动态规划】背包问题】 https://www.bilibili.com/video/BV1K4411X766/?share_source=copy_web&vd_source=7e63f1b6fa68c511b241d12721f0a4bc)
先从一个具体例子入手

对于所给定的背包容量和物品状态,我们需要找出价值最大的一个组合,通过画图
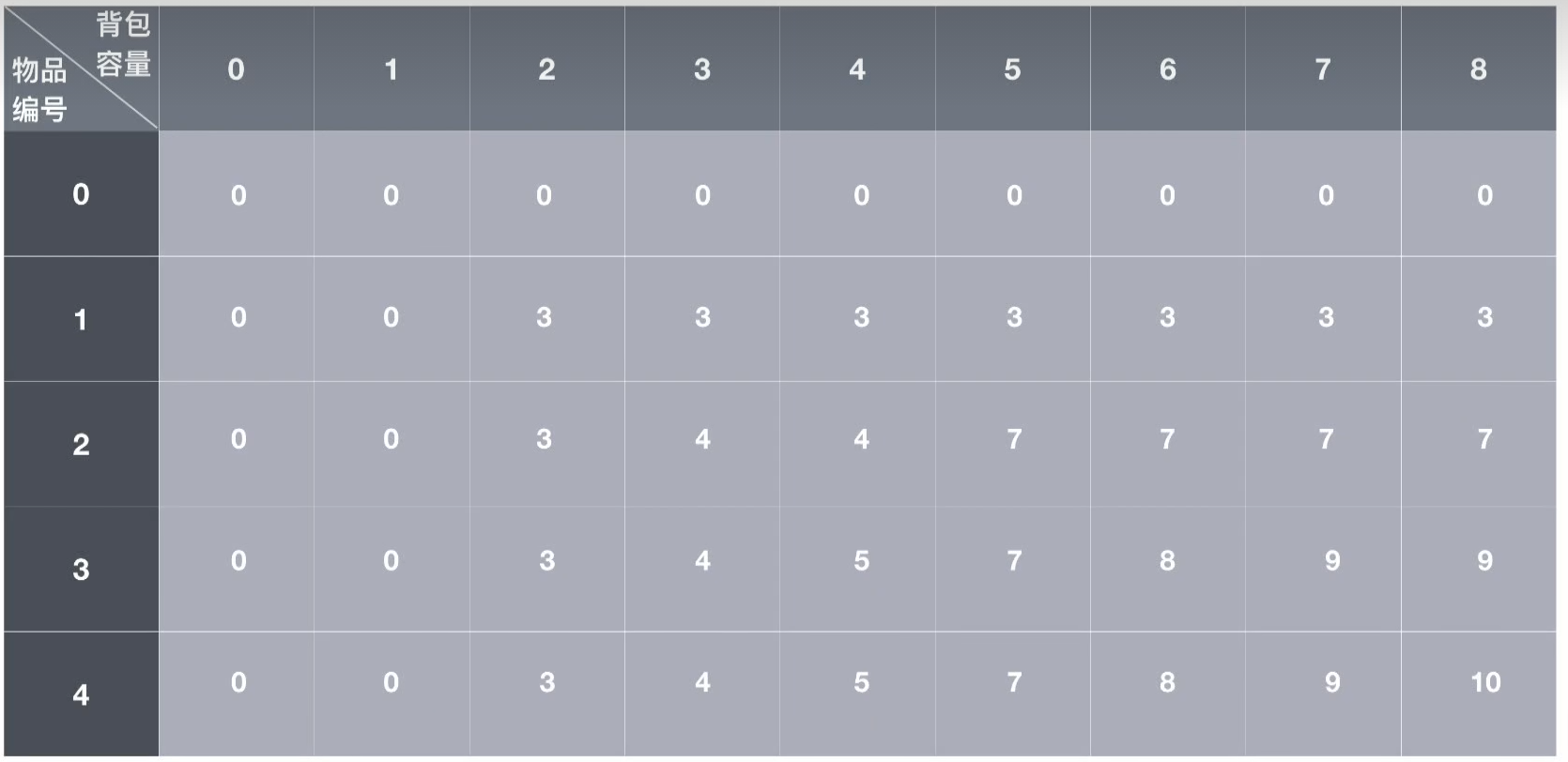
假设这是一个f(i,j)的数组,则每一个f(i,j)的值都是前i(物品编号)件物品中,不超过j(背包容量)体积下的最大值
注意:重中之重,每个格子是只考虑前i件物品 当时我比较不能理解的是为什么只考虑前i件物品下不超过该体积的值,编号i之后的物品不也可以放入该体积容量,假如该方法价值更高,那不是就不是该背包体积下最大价值了。
当时就是不能理解啊,后面思考之后终于悟了,表格是所有情况都能考虑到,因为每个格子是在选了和不选的情况下取的最大值,我们只要只考虑前i件物品,后面每一个格子就能由前面的推出来,也能得到一个公式。
比如这题假如我们要算第f(4,8)的值,也就是该条件的最大价值,假设我们不知道该值,前面的数据我们都是知道的,因此第4件物品有选和不选两种情况,如果不选,f(4,8)=f(3,8),本来需要考虑前4个,现在只需要考虑前3个,而f(3,8)前面是已经算出来了。假如选,则需要满足一个条件,即此时背包剩余的容量一定大于第四件物品体积,在此前提下,我们选了第4件物品,然后往前找,选了4之后我们表格应该找到f(3,8-第四件物品体积)也就是f(3,3),此时只考虑前3个物品,即f(4,8)=第四件物品价值+f(3,3),因为前面的f都是已经计算出来对应条件的价值最大值了,f(4,8)的值也就出来了。最后,在选和不选中取一个最大值即使f(4,8)的值。
用表格容易理解,但确定是该方法不容易运用到其他同题型中,下面给出第二种
2.闫式DP分析法
此方法比较有规律和逻辑,但对于新手不容易理解(nnd当时我看了好多遍才懂),但是第一种懂了,第二种也应该学习,因为该方法会了之后同题型就变得很简单了,后面我也会发类似题目的博客,用该方法来做,会发现简单很多。
大致思路与第一种是差不多的,也是把f(i,j)分为两种情况,这里不多做解释,和第一种同理
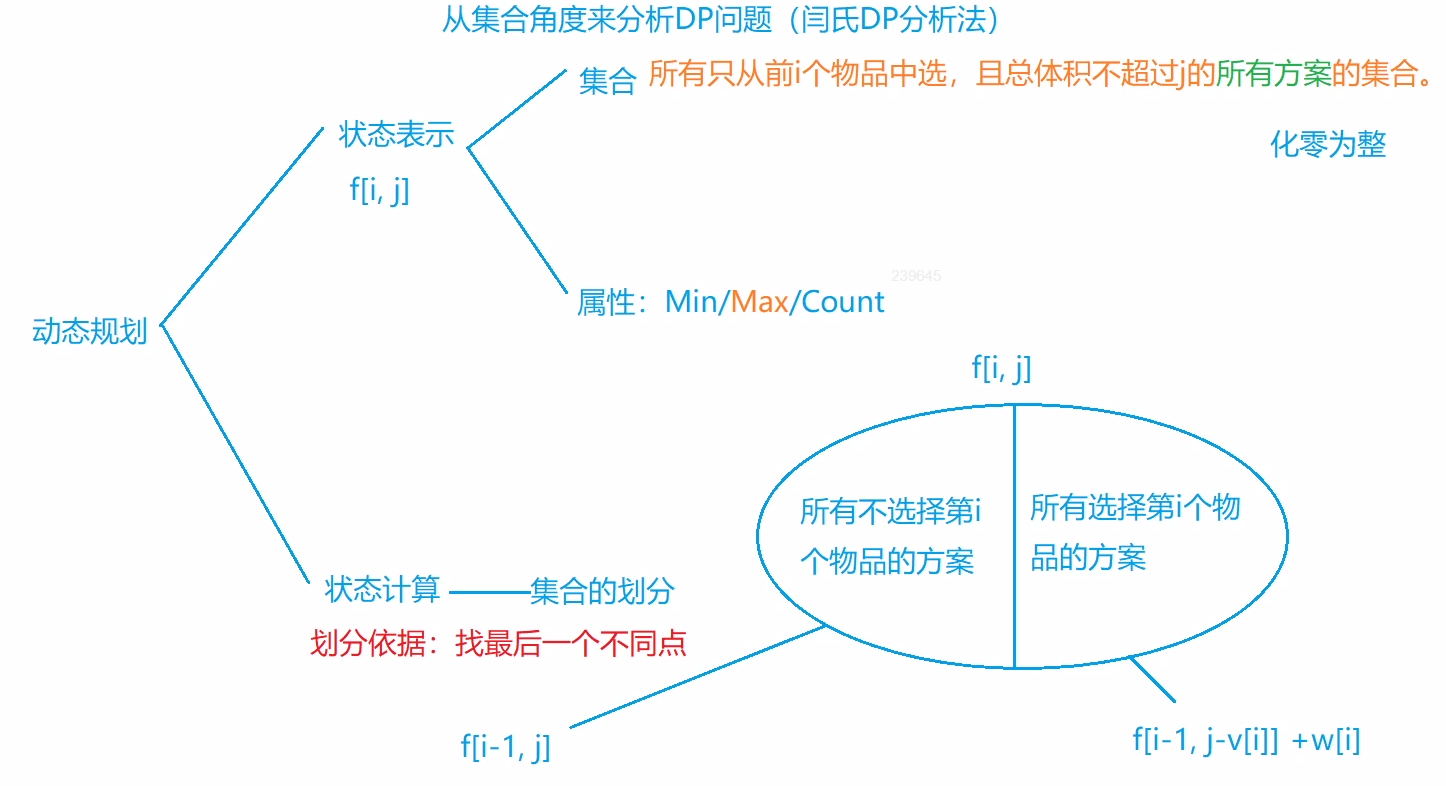
该方法很系统的对于该类题型的做题方法做了一个总结,此时f(i,j)为一个集合,每个f(i,j)的内容需要其属性来判断,背包问题要求我们找最大值,即属性为max,因此f(i,j)为对应条件下的最大值,然后进行状态计算,如何计算f(i,j),找到最后一个不同点进行划分,对于其他题型我们只需要对f(i,j)进行不同情况的划分考虑完就可以了。
状态计算的核心:如何将现有的集合划分为更小的子集,使得所有子集都可以计算出来,这是我们需要做的事
说了这么多,没有代码就是空谈
代码如下:(第一种和第二种方法都一样代码)
#include<iostream>
using namespace std;
const int N=1010;
int f[N][N];
int v[N],w[N];
int main()
{int n,m;cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++)//i代表物品,第一件开始考虑for(int j=0;j<=m;j++)//j代表背包容量,可以为0(一件都不选),因此从0开始{f[i][j]=f[i-1][j];//不选第i个物品if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);//选第i个物品}cout<<f[n][m]<<endl;return 0;
}对于该代码我们是可以进行优化的,把二维转化为一维可以节省空间和时间,这里也给出优化后的代码,想要了解为什么的这里也给出一个链接https://www.acwing.com/solution/content/1374/,里面解释的非常好,这里我就不多阐明
优化后的代码:
#include<iostream>
using namespace std;
const int N=1010;
int f[N];
int v[N],w[N];
int main()
{int n,m;cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++)for(int j=m;j>=v[i];j--)//这里为什么从后往前遍历,因为为了防止第i层前面先被更新{f[j]=max(f[j],f[j-v[i]]+w[i]);}cout<<f[m]<<endl;return 0;
}最后祝大家早日理解背包问题,把动态规划用的行云流水,以后也会常更新dp的!!!
相关文章:

01背包问题(大彻大悟版)
背包问题身为一个非常经典的动态规划问题,理清思路很重要,在经过多次观看y总视频和b站解析,加上CSDN的文章辅助,我终于从很多不理解到大彻大悟,下面是我对于背包问题思路的总结,有问题的话欢迎指出。谈到背…...

【麒麟服务器操作系统忘记开机密码怎么办?---银河麒麟服务器操作系统更改用户密码】
银河麒麟服务器操作系统更改用户密码 1.启动主机进入 grub 菜单,如图 1.1 以最新版本 Kylin-Server-10-SP2-x86-Release-Build09-20210524 为例。 图 1.1 grub 菜单 2 编辑 kernel 2.1按下”e”输入,输入用户名和密码(root/Kylin123123&…...
考点分类)
华为OD机试(20222023)考点分类
字符串,数组,集合操作 题库分值序号题目考点 or 实现Old1001敏感字段加密字符串,数组,集合操作Old1002IPv4地址转换成整数字符串,数组,集合操作Old1006字符串分割字符串,数组,集合操作Old1007...

初级篇 3 - HTML 或 CSS 文件中不懂的标签属性详解
目录一、遇到的不懂的标签属性详解1、meta 标签的 http-equiv 属性(元标签)二、遇到的 CSS 不懂的属性详解vertical-align三、如何规避 HTML 自动换行 - 脱离文档流配置属性 display: inline-block理解 inline、inline-block、blockinline总结:四、导航栏自动弹出子…...

【C语言】每日刷题 —— 牛客语法篇(4)
🚀🚀前言 大家好,继续更新专栏 c_牛客,不出意外的话每天更新十道题,难度也是从易到难,自己复习的同时也希望能帮助到大家,题目答案会根据我所学到的知识提供最优解。 🏡个人主页&am…...
HashMap ConcurrentHashMap介绍
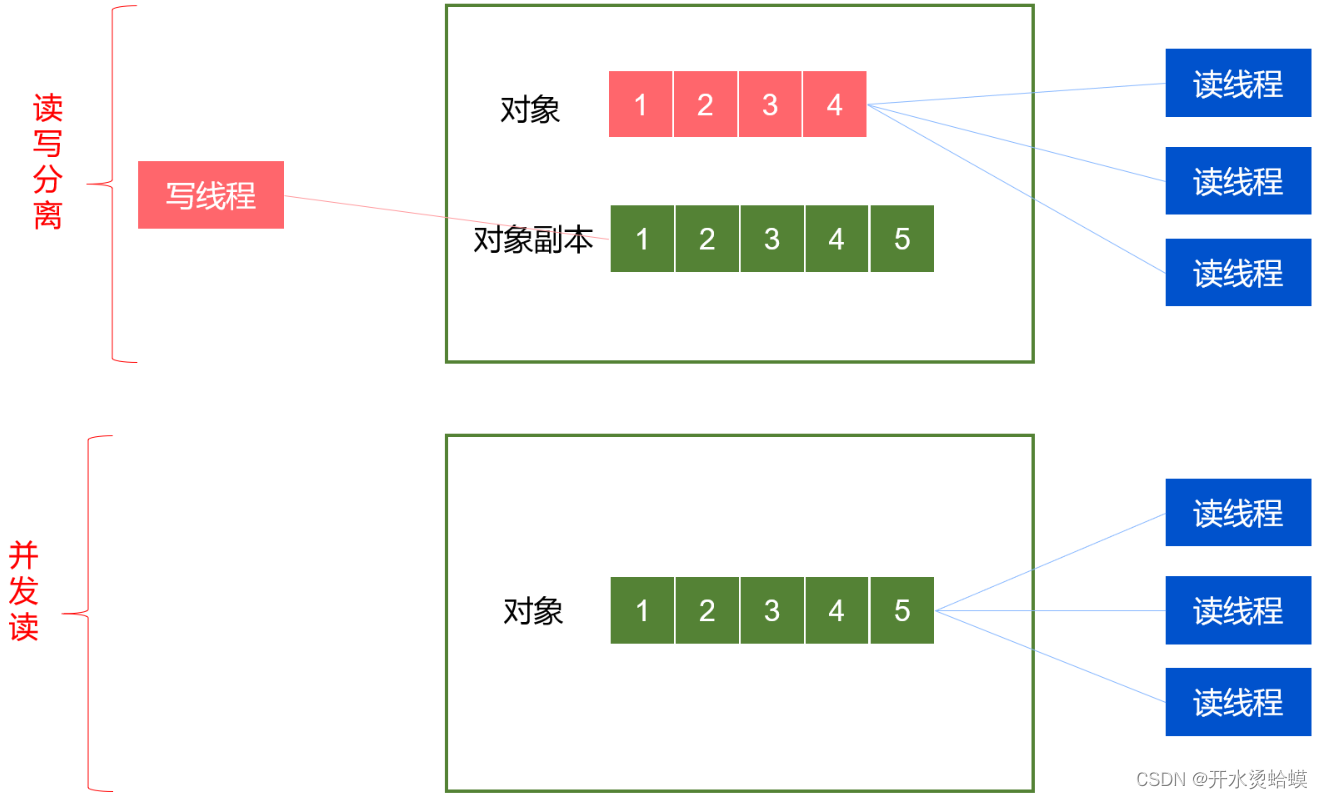
目录 HashMap 数据结构 重要成员变量 Jdk7-扩容死锁分析 单线程扩容 多线程扩容 Jdk8-扩容 ConcurrentHashMap 数据结构 并发安全控制 源码原理分析 重要成员变量 协助扩容helpTransfer 扩容transfer 总结 CopyOnWrite机制 源码原理 HashMap 数据结构 数组…...

C++语法规则3(C++面向对象)
多态 C多态意味着调用成员函数时,会根据调用函数的对象的类型来执行不同的函数; 形成多态必须具备三个条件: 必须存在继承关系;继承关系必须有同名虚函数(其中虚函数是在基类中使用关键字 virtual 声明的函数&#…...
Python tkinter 如何实现网站下载工具?将所有数据一键获取
前言 铁汁们有没有想过,如何把几个代码的功能结合到一起呢? 有想过的话,有没有实现过呢? 其实很简单的啊,咱就写一个界面就好了,想要哪个代码运行,鼠标轻轻一点就行 开发环境 python 3.8: 解…...
第六章:C语言数据结构与算法初阶之栈
系列文章目录 文章目录系列文章目录前言一、栈二、栈的实现三、接口函数的实现1、初始化2、销毁栈3、压栈与出栈4、判空5、元素个数6、返回栈顶元素四、栈中元素的访问总结前言 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。 一、…...

Android学习之WebView
什么是WebView WebView是Android中UI组件的一种,WebView基于webkit内核,不过由于兼容性的原因在Android5.0后改为了Chromium内核。 WebView可以用来展示网页,常用于我们不想打开浏览器但又想浏览网页的情况。 WebView的使用 WebVeiw的常用…...

3/11 考试总结
时间安排 7:30–7:50 读题,T1 是个利用随机性的题目,T2 dp,T3 不知道是啥。 7:50–8:30 T1,对于随机有个结论时最值突变不超过 log ,于是可以处理出所有 log 个区间然后统计答案,但这暴力做是个 3log 铁定过不去。 8:30–8:50 T2…...

Leetcode 141.环形链表 142环形链表II
141环形链表 文章目录快慢指针快慢指针 代码思路: slow 和fast 指向 head slow走一步,fast走两步 没有环: fast每次走2步 ,如果 fast 最终遇到NULL(链表中的元素是 偶数)或者fast->next(链表中的元素是 奇数)遇到NULL…...
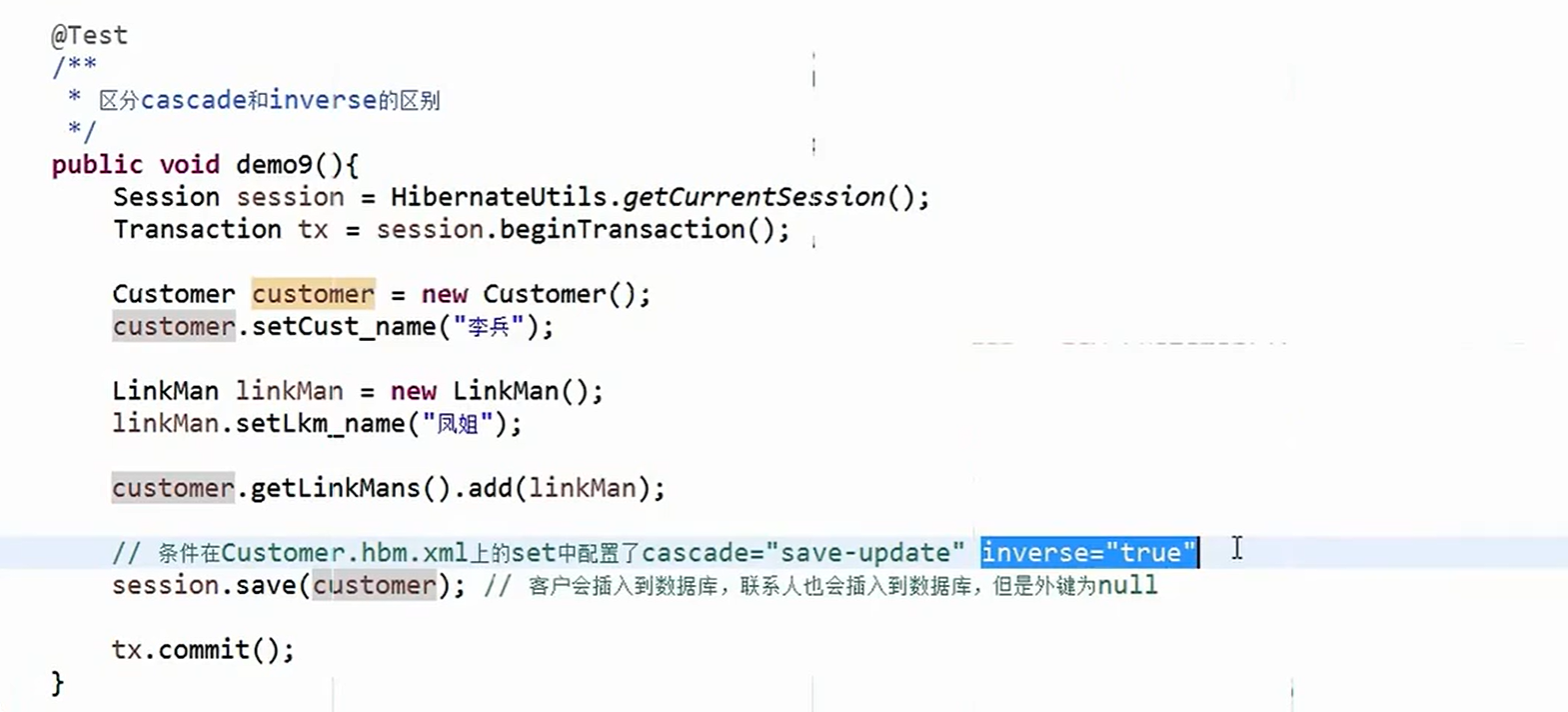
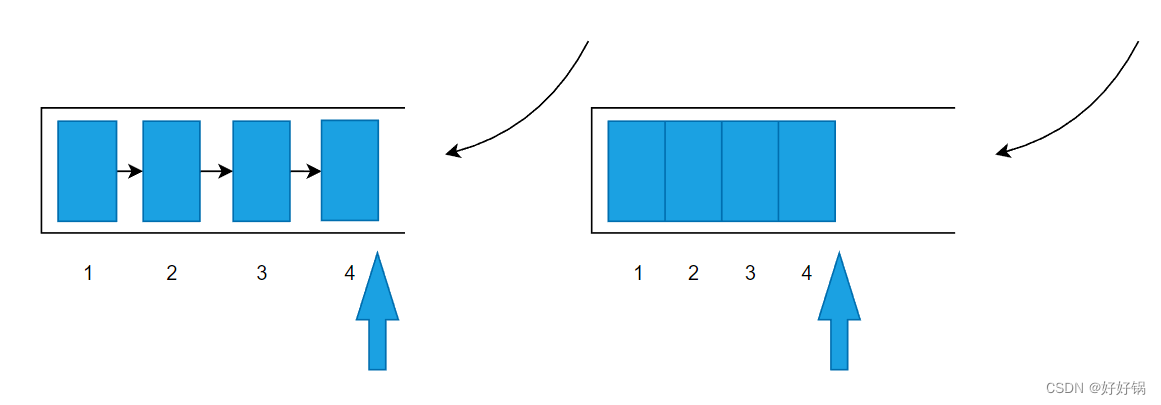
hibernate学习(五)
hibernate学习(五) hibernate的一对多关联映射: 一、数据库表与表之间关系 一对多建表原则: 多对多的建表原则: 一对一建表原则: (1)唯一外键对应: (…...

STM32CubeIDE 快速开发入门指南
描述 STM32CubeIDE是一体式多操作系统开发工具,是STM32Cube软件生态系统的一部分。 STM32CubeIDE是一种高级C/C开发平台,具有STM32微控制器和微处理器的外设配置、代码生成、代码编译和调试功能。它基于Eclipse/CDT™框架和用于开发的GCC工具链…...
【独家】)
华为OD机试 - 火星文计算(C 语言解题)【独家】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 使用说明本期题目:火星文计…...

超超超超保姆式详解——字符函数和字符串函数(学不会打我)上
目录 长度不受限制的字符串函数 strlen部分 strlen函数的易错小知识 strlen函数的实现 strcpy部分 strcat部分 自己实现strcat strstr函数部分 简单例子: 分析 strcmp部分 长度受限制的字符串函数 strncpy 简单例子 strncat strncmp 简单例子 &…...

Data mesh 笔记
有用的网站 https://www.datamesh-architecture.com/ https://www.agilelab.it/data-mesh-in-action https://learn.microsoft.com/en-us/azure/cloud-adoption-framework/scenarios/cloud-scale-analytics/well-architected-framework https://www.datamesh-architecture.com…...
大白话透彻研究通过explain命令得到的SQL执行计划(2))
(八十三)大白话透彻研究通过explain命令得到的SQL执行计划(2)
今天我们就一步一步的来讲解不同的SQL语句的执行计划长什么样子,先来看第一条SQL语句,特别的简单,就是: explain select * from t1 就这么一个简单的SQL语句,那么假设他这个里面有大概几千条数据,此时执行计…...

案例18-面向对象之开门小例子
目录 一:背景介绍 二:思路&方案 1.面向过程 2.面向对象 3.面向对象(反射) 三:过程 1.面向过程:原本何老师的作用交给我了米老师来完成。 2.面向对象:把开门的方法完全交个何老师,米老师不需要有…...
【碎片化知识总结】三月第一周
目录 前言 1、开发中常用的 IDEA 编辑器,如何做到不用每次都重新配置? 2、如何使用 Python 获取视频文件信息? 3、使用 Java 的 try-with-resources 优化代码 4、使用 shell 脚本批量修改服务器某一目录下的文件后缀名称 5、MySQL优化&…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
