数据结构历年考研真题对应知识点(树的基本概念)
目录
5.1树的基本概念
5.1.2基本术语
【森林中树的数量、边数和结点数的关系(2016)】
5.1.3树的性质
【树中结点数和度数的关系的应用(2010、2016)】
【指定结点数的三叉树的最小高度分析(2022)】
5.1树的基本概念
5.1.2基本术语
下面结合图5.1中的树来说明一些基本术语和概念。
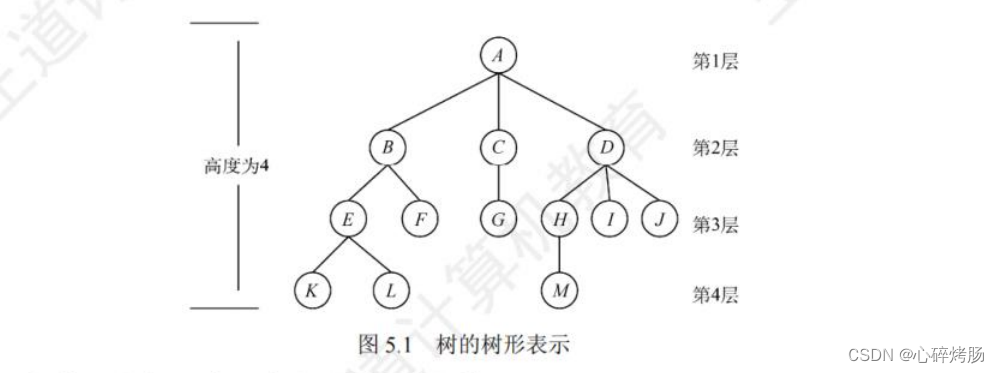
1)祖先、子孙、双亲、孩子、兄弟和堂兄弟。
祖先:考虑结点K,从根A到结点K的唯一路径上的所有其他结点,称为结点K的祖先。
子孙:如结点B是结点K的祖先,而K是B的子孙,结点B的子孙包括EFK.L。
双亲:路径上最接近结点K的结点E称为K的双亲,而K为E的孩子。根A是树中唯一没有双亲的结点。
兄弟:有相同双亲的结点称为兄弟,如结点K和结点L有相同的双亲E,即K和L为兄弟。
堂兄弟:双亲在同一层的结点互为堂兄弟,结点G与E,E,H,I,J互为堂兄弟。
2)结点的度和树的度。
树中一个结点的孩子个数称为该结点的度,树中结点的最大度数称为树的度。如结点B的度为 2,结点D的度为3,树的度为3。
3)分支结点和叶结点。
度大于0的结点称为分支结点(又称非终端结点);度为0(没有孩子结点)的结点称为叶结点(又称终端结点)。在分支结点中,每个结点的分支数就是该结点的度。
4)结点的深度、高度和层次。
结点的层次:从树根开始定义,根结点为第1层,它的孩子为第2层,以此类推。
结点的深度:就是结点所在的层次。
树的高度(或深度):是树中结点的最大层数。图5.1中树的高度为4。
结点的高度:是以该结点为根的子树的高度。
5)有序树和无序树。
树中结点的各子树从左到右是有次序的,不能互换,称该树为有序树,否则称为无序树。
假设图 5.1为有序树,若将子结点位置互换,则变成一棵不同的树。
6)路径和路径长度。
树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的,而路径长度是路径上所经过的边的个数。
注意:因为树中的分支是有向的,即从双亲指向孩子,所以树中的路径是从上向下的,同一双亲的两个孩子之间不存在路径。
7)森林
【森林中树的数量、边数和结点数的关系(2016)】
森林是 m(m≥0)棵互不相交的树的集合。森林的概念与树的概念十分相近,因为只要把树的根结点删去就成了森林。反之,只要给m棵独立的树加上一个结点,并把这 m棵树作为该结点的子树,则森林就变成了树。
注意:上述概念无须刻意记忆,根据实例理解即可。考研时不大可能直接考查概念,而都是结合具体的题目考查。做题时,遇到不熟悉的概念可以翻书,练习得多自然就记住了。
5.1.3树的性质
树具有如下最基本的性质:
【树中结点数和度数的关系的应用(2010、2016)】
1)树的结点数n等于所有结点的度数之和加1。
结点的度是指该结点的孩子数量,每个结点与其每个孩子都由唯一的边相连,因此树中所有结点的度数之和等于树中的边数之和。
树中的结点(除根外)都有唯一的双亲,因此结点数 n等于边数之和加1,即所有结点的度数之和加1。
2)度为m的树中第i层上至多有 个结点(i => 1)。
第1层至多有1个结点(即根结点),第2层至多有m个结点,第3层至多有㎡个结点,以此类推。使用数学归纳法可推出第i层至多有个结点。
3)高度为h的 m 叉树至多有个结点。
当各层结点数达到最大时,树中至多有个结点。
【指定结点数的三叉树的最小高度分析(2022)】
4)度为 m、具有n个结点的树的最小高度h为
为使树的高度最小,在前 h-1 层中,每层的结点数都要达到最大,前 h-1 层最多有个结点,前h层最多有
个结点。因此
,即
,
解得 。
5)度为 m、具有n个结点的树的最大高度h为n-m+1。
由于树的度为 m,因此至少有一个结点有 m个孩子,它们处于同一层。为使树的高度最大,其他层可仅有一个结点,因此最大高度(层数)为n-m+1。由此,也可逆推出高度为 h、度为m的树至少有 h+m-1 个结点。
相关文章:
数据结构历年考研真题对应知识点(树的基本概念)
目录 5.1树的基本概念 5.1.2基本术语 【森林中树的数量、边数和结点数的关系(2016)】 5.1.3树的性质 【树中结点数和度数的关系的应用(2010、2016)】 【指定结点数的三叉树的最小高度分析(2022)】 5.1…...

Pytorch和Tensorflow安装【Win和Linux】
Ubuntu/win安装Pytorch和Tensorflow 说明: 这两种框架的搭建,均基于Anaconda进行搭建。先在系统中安装Anaconda软件。 一、Pytorch的搭建 windows安装 (1)搭建参考官网给的命令,pytorch官网 (2)下载地址:https://download.pytorch.org/whl/torch_stable.html 从上述…...

筑算网基石 创数智未来|锐捷网络闪耀2024 MWC上海
2024年6月26日至28日,全球科技界瞩目的GSMA世界移动大会(MWC 上海)在上海新国际博览中心(SNIEC)盛大召开。作为行业领先的网络解决方案提供商,锐捷网络以“筑算网基石 创数智未来”为主题,带来了…...

T4打卡 学习笔记
所用环境 ● 语言环境:Python3.11 ● 编译器:jupyter notebook ● 深度学习框架:TensorFlow2.16.1 ● 显卡(GPU):NVIDIA GeForce RTX 2070 设置GPU from tensorflow import keras from tensorflow.keras…...
抖音矩阵云混剪系统源码 短视频矩阵营销系统V2(全开源版)
>>>系统简述: 抖音阵营销系统多平台多账号一站式管理,一键发布作品。智能标题,关键词优化,排名查询,混剪生成原创视频,账号分组,意向客户自动采集,智能回复,多…...
zabbix报警机制
zabbix思路流程...

【Matlab】-- 飞蛾扑火优化算法
文章目录 文章目录 01 飞蛾扑火算法介绍02 飞蛾扑火算法伪代码03 基于Matlab的部分飞蛾扑火MFO算法04 参考文献 01 飞蛾扑火算法介绍 飞蛾扑火算法(Moth-Flame Optimization,MFO)是一种基于自然界飞蛾行为的群体智能优化算法。该算法由 Sey…...

全面体验ONLYOFFICE 8.1版本桌面编辑器
ONLYOFFICE官网 在当今的数字化办公环境中,选择合适的文档处理工具对于提升工作效率和团队协作至关重要。ONLYOFFICE 8.1版本桌面编辑器,作为一款集成了多项先进功能的办公软件,为用户提供了全新的办公体验。今天,我们将深入探索…...

建议csdn赶紧将未经作者同意擅自锁住收费的文章全部解锁,别逼我用极端手段让你们就范
前两天我偶然发现csdn竟然将我以前发表的很多文章锁住向读者收费才让看。 csdn这种无耻行径往小了说是侵犯了作者的版权著作权,往大了说这是在打击我国IT领域未来的发展,因为每一个做过编程工作的人都知道,任何一个程序员的学习成长过程都少不…...

Pycharm一些问题解决办法
研究生期间遇到关于Pycharm一些问题报错以及解决办法的汇总 ModuleNotFoundError: No module named sklearn’ 安装机器学习库,需要注意报错的sklearn是scikit-learn缩写。 pip install scikit-learnPyCharm 导包提示 unresolved reference 描述:模块…...
ONLYOFFICE 桌面编辑器 8.1 发布:全新 PDF 编辑器、幻灯片版式、增强 RTL 支持及更多本地化选项
目录 什么是ONLYOFFICE? ONLYOFFICE 主要特点包括: 官网信息: 1. 功能齐全的 PDF 编辑器 1.1 编辑 PDF 文本 1.2 插入和修改对象 1.3 创建和填写表单 2. 幻灯片版式功能 2.1 快速应用幻灯片版式 2.2 动画窗格的改进 3. 文档编辑、…...
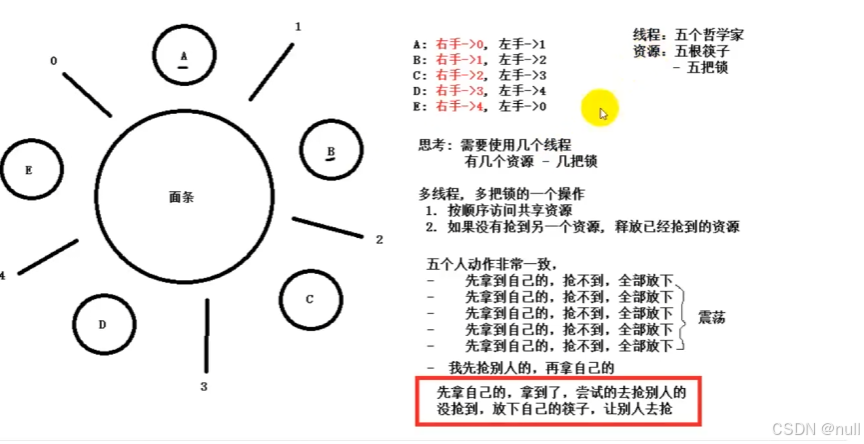
Linux高并发服务器开发(六)线程
文章目录 1. 前言2 线程相关操作3 线程的创建4 进程数据段共享和回收5 线程分离6 线程退出和取消7 线程属性(了解)8 资源竞争9 互斥锁9.1 同步与互斥9.2 互斥锁 10 死锁11 读写锁12 条件变量13 生产者消费者模型14 信号量15 哲学家就餐 1. 前言 进程是C…...
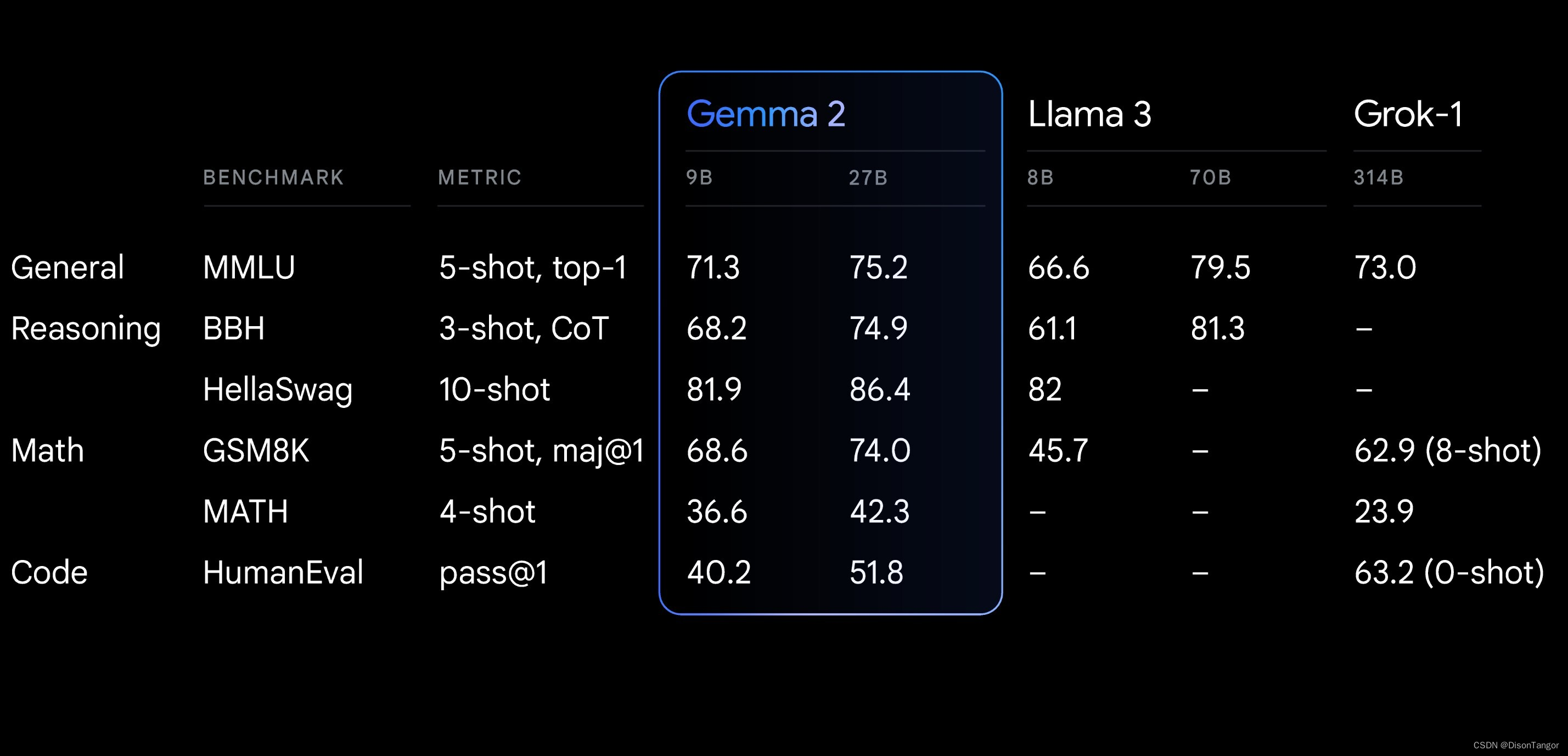
Google发布Gemma 2轻量级开放模型 以极小的成本提供强大的性能
除了 Gemini 系列人工智能模型外,Google还提供 Gemma 系列轻量级开放模型。今天,他们发布了 Gemma 2,这是基于全新架构设计的下一代产品,具有突破性的性能和效率。 Gemma 2 有两种规格:90 亿 (9B) 和 270 亿 (27B) 个参…...
精品UI知识付费系统源码网站EyouCMS模版源码
这是一款知识付费平台模板,后台可上传本地视频,批量上传视频连接, 视频后台可设计权限观看,免费试看时间时长,会员等级观看,付费观看等功能, 也带软件app权限下载,帮助知识教育和软件…...

使用Apache POI库在Java中导出Excel文件的详细步骤
使用Apache POI库在Java中导出Excel文件的详细步骤 学习总结 1、掌握 JAVA入门到进阶知识(持续写作中……) 2、学会Oracle数据库入门到入土用法(创作中……) 3、手把手教你开发炫酷的vbs脚本制作(完善中……) 4、牛逼哄哄的 IDEA编程利器技…...

基于C#在WPF中使用斑马打印机进行打印
最近在项目中接手了一个比较有挑战性的模块——用斑马打印机将需要打印的内容打印出来。苦苦折腾了两天,总算有所收获,就发到网上来骗骗分数-_-|| 项目中使用的打印机型号为GX430t的打印机,接手的时候,自己对于打印机这块儿是眼前…...

六、资产安全—信息分级资产管理与隐私保护练习题(CISSP)
六、资产安全—信息分级资产管理与隐私保护(CISSP): 六、资产安全—信息分级资产管理与隐私保护(C...

使用 AutoGen 的 AI 智能体设计模式
1.Auto Gen框架 在Auto中,每种智能体分别扮演不同的角色。 ConversableAgent 作为最高级别的智能体抽象,为所有具体智能体提供了基础的通信能力。这包括发送和接收信息的能力,以及基于这些信息进行内部状态更新的能力。所有从这个类派生的智能体都继承了这些基本功能…...

Android InputChannel连接
InputChannel是InputDispatcher 和应用程序 (InputTarget) 的通讯桥梁,InputDispatcher 通知应用程序有输入事件,通过InputChannel中的socket进行通信。 连接InputDispatcher和窗口 WinodwManagerService:addwindow: WMS 添加窗口时,会创建…...

爬虫笔记17——selenium框架的使用
selenium框架的使用 1、python程序安装selenium框架2、下载Chrome谷歌驱动3、selenium的基本使用4、多个标签页切换顺序混乱的问题 1、python程序安装selenium框架 # 在安装过程中最好限定框架版本为4.9.1 # pip install selenium 没有制定版本,非镜像下载也会比较…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
