算法基础--------【图论】
图论(待完善)
DFS:和回溯差不多
BFS:进while进行层序遍历
定义: 图论(Graph Theory)是研究图及其相关问题的数学理论。图由节点(顶点)和连接这些节点的边组成。图论的研究范围广泛,涉及路径、流、匹配、着色等诸多问题。
特点:
节点和边: 图论问题通常围绕节点(点)和边(线)展开,研究它们之间的关系。
图的种类: 包括无向图、有向图、加权图等不同类型的图,每种图有不同的应用场景。
算法: 常见的图论算法包括深度优先搜索(DFS)、广度优先搜索(BFS)、最短路径算法(如Dijkstra算法、Floyd-Warshall算法)、最小生成树算法(如Kruskal算法、Prim算法)等。(Dijkstra华子暑期实习笔试考了)
适用范围: 广泛用于网络分析、路径规划、资源分配等领域,如社交网络、交通系统、计算机网络等。(网络分析,路径规划这个真的很爱考)
示例: 最短路径问题(如寻找城市之间的最短路线)是一个经典的图论问题,通常用Dijkstra算法或Bellman-Ford算法解决。
【200】岛屿数量
要么用DFS的思想,要么用BFS层序遍历的思想
DFS:节点有四个方向,都遍历一遍,我写的逻辑是先下右上左。
dfs方法: 设目前指针指向一个岛屿中的某一点 (i, j),寻找包括此点的岛屿边界。
从 (i, j) 向此点的上下左右 (i+1,j),(i-1,j),(i,j+1),(i,j-1) 做深度搜索。
终止条件:
(i, j) 越过矩阵边界;
grid[i][j] == 0,代表此分支已越过岛屿边界。
搜索岛屿的同时,执行 grid[i][j] = ‘0’,即将岛屿所有节点删除,以免之后重复搜索相同岛屿。
主循环:
遍历整个矩阵,当遇到 grid[i][j] == ‘1’ 时,从此点开始做深度优先搜索 dfs,岛屿数 count + 1 且在深度优先搜索中删除此岛屿。
最终返回岛屿数 count 即可。
DFS:
class Solution {
public:int numIslands(vector<vector<char>>& grid) {if(grid.size() == 0 || grid[0].size() == 0)return 0;int m = grid.size(),n = grid[0].size();vector<vector<int>> vec;int res =0;for(int i =0;i<m;i++){vector<int> tempvec;for(int j=0;j<n;j++){ int tmp = grid[i][j]-'0';tempvec.push_back(tmp);//转化成int类型的}vec.push_back(tempvec);} for(int i =0;i<m;i++){for(int j=0;j<n;j++){if( vec[i][j] == 1){dfs(vec,i,j);//dfs的次数就是岛屿的数量res++;}}} return res;}
private:void dfs(vector<vector<int>>& vec,int i, int j){if(i<0 || j<0 || i>vec.size()-1 || j>vec[0].size()-1)return;cout<<"(i,j) = "<<i<<j<<","<<vec[i][j]<<endl;if(vec[i][j] != 1)return;vec[i][j] =-1;//标记dfs(vec,i+1,j);dfs(vec,i,j+1);dfs(vec,i-1,j);dfs(vec,i,j-1);}
};
int main() {Solution s;vector<vector<char>> grid = {{'1','1','1','1','0'},{'1','1','0','1','0'},{'1','1','0','0','0'},{'0','0','0','0','0'}};s.numIslands(grid);system("pause");return 0;
}
BFS:
借用一个队列 queue,判断队列首部节点 (i, j) 是否未越界且为 1:
若是则置零(删除岛屿节点),并将此节点上下左右节点 (i+1,j),(i-1,j),(i,j+1),(i,j-1) 加入队列;
若不是则跳过此节点;
循环 pop 队列首节点,直到整个队列为空,此时已经遍历完此岛屿。
class Solution {
public:int numIslands(vector<vector<char>>& grid) {if (grid.empty() || grid[0].empty()) return 0;int m = grid.size(), n = grid[0].size();int res = 0;queue<pair<int, int>> q;for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {if (grid[i][j] == '1') {q.push({i,j});grid[i][j] = '0'; // 标记为已访问 加入就标记res++;//第一层更新while (!q.empty()) {//BFS遍历int x = q.front().first, y = q.front().second;q.pop();for (const auto& dir : dirs) {int nx = x + dir.first, ny = y + dir.second;if (nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] == '1') {q.push({nx,ny});grid[nx][ny] = '0'; // 标记为已访问}}}}}}return res;}
private:vector<pair<int, int>> dirs{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};};
【994】腐烂的橘子
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
- 值
0代表空单元格; - 值
1代表新鲜橘子; - 值
2代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
示例 1:
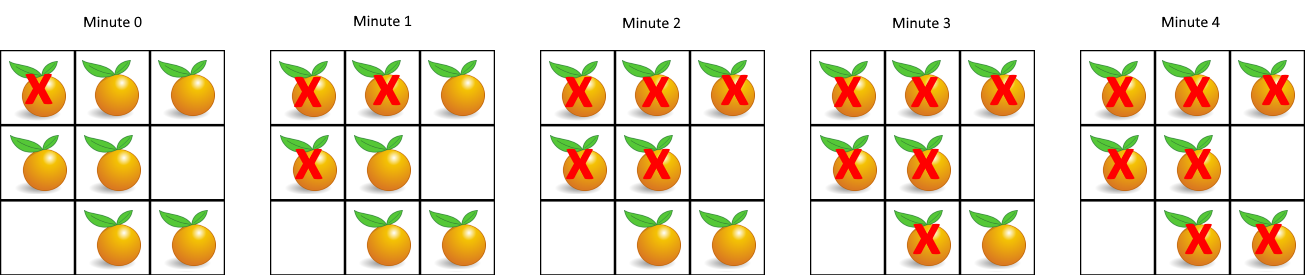
输入:grid = [[2,1,1],[1,1,0],[0,1,1]]
输出:4
class Solution {
public:int orangesRotting(vector<vector<int>>& grid) {if(grid.size() == 0 ||grid[0].size() ==0)return -1;int m = grid.size();int n = grid[0].size();int min = 0;//分钟数int fresh = 0;//新鲜橘子queue<pair<int,int>> q;//存储腐烂的橘子for(int i =0;i<m;i++){for(int j =0;j<n;j++){if(grid[i][j] == 2){q.push({i,j});}else if(grid[i][j] == 1){//统计新鲜橘子fresh++;}}}// if(q.empty() || fresh==0 )return -1;//没有腐烂的橘子 没有新鲜的橘子vector<pair<int,int>> dirs = {{1,0},{0,1},{0,-1},{-1,0}};while(!q.empty()){//每一层int qsize = q.size();//有n个烂橘子bool flag = false;for(int i =0;i<qsize;i++){//遍历这n个烂橘子int x = q.front().first;int y = q.front().second;q.pop();for(auto dir:dirs){int nx = dir.first+x;int ny = dir.second+y;if(nx >=0 && nx<m && ny >=0 && ny<n && grid[nx][ny]==1){q.push({nx,ny});grid[nx][ny] = 2;fresh--;//到最后要没有新鲜橘子才结束flag = 1;//有新鲜橘子就标记}}}//一层就要++if(flag)min++;//有新鲜橘子才++}return fresh? -1:min;}
};
总结:腐烂的橘子是以各个腐烂的橘子为头结点开始入队遍历的,而岛屿数量是以有无1直接入队遍历。
相关文章:

算法基础--------【图论】
图论(待完善) DFS:和回溯差不多 BFS:进while进行层序遍历 定义: 图论(Graph Theory)是研究图及其相关问题的数学理论。图由节点(顶点)和连接这些节点的边组成。图论的研究范围广泛,涉及路径、…...

x86和x64架构的区别及应用
x86和x64架构的区别及应用 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 在计算机硬件和软件领域,x86和x64是两种常见的处理器架构。它们在计算能…...

2024年度总结:不可错过的隧道IP网站评估推荐
随着网络技术的飞速发展,隧道IP服务成为了许多企业和个人在进行网络活动时的得力助手。作为专业的测评团队,我们经过一整年的深入研究和测试,为大家带来了三款备受瞩目的隧道IP网站推荐——品易HTTP、极光HTTP和一G代理。接下来,我…...

Linux下VSCode的安装和基本使用
应用场景:嵌入式开发。 基本只需要良好的编辑环境,能支持文件搜索和跳转,就挺OK的。 之所以要在Linux下安装,是因为在WIN11上安装后,搜索功能基本废了,咋弄都弄不好,又不方便重装win系统&#x…...
C# 实现websocket双向通信
🎈个人主页:靓仔很忙i 💻B 站主页:👉B站👈 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:C# 🤝希望本文对您有所裨益,如有不足之处ÿ…...

Spring Boot结合FFmpeg实现视频会议系统视频流处理与优化
在构建高效稳定的视频会议系统时,实时视频流的处理和优化是开发者面临的核心挑战之一。这不仅仅是简单的视频数据传输,更涉及到一系列复杂的技术问题,需要我们深入分析和有效解决。 高并发与实时性要求: 视频会议系统通常需要支持多人同时进行视频通话,这就意味着系统需要…...

扫扫地,搞搞卫生 ≠ 车间5S管理
在制造业的日常运营中,车间管理是一项至关重要的工作,它直接关系到生产效率、产品质量以及员工的工作环境。然而,许多人常常将简单的“扫扫地,搞搞卫生”等同于车间5S管理,这种误解不仅可能导致管理效果不佳࿰…...
)
ES(笔记)
es就是json请求体代替字符串查询 dsl查询和过滤,一个模糊查询,一个非模糊查询 must,should 做模糊查询的,里面都是match,根据查询内容进行匹配,filter过滤,term词元查询,就是等值查…...
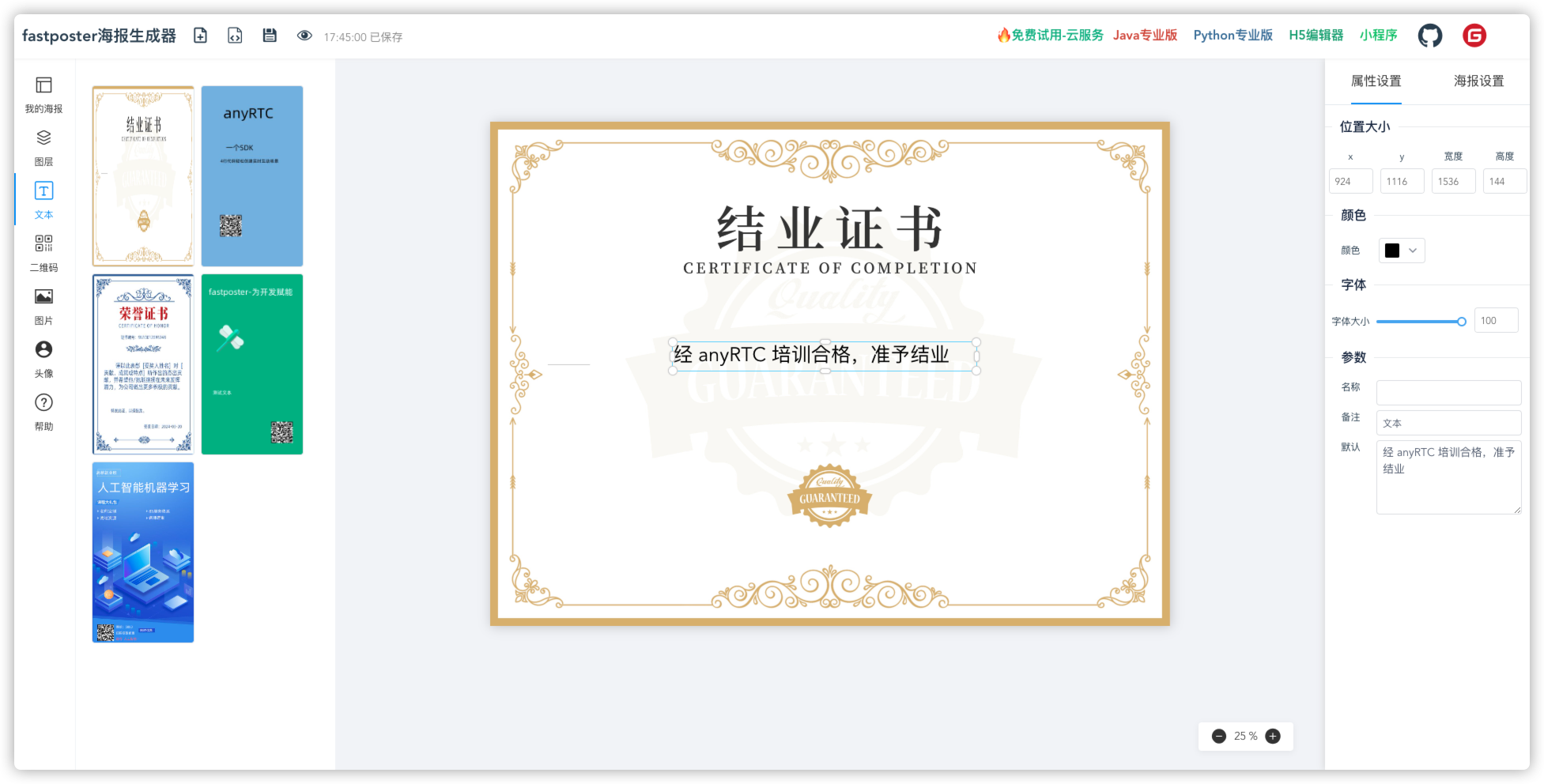
开箱即用的fastposter海报生成器
什么是 fastposter ? fastposter 海报生成器是一款快速开发海报的工具。只需上传一张背景图,在对应的位置放上组件(文字、图片、二维码、头像)即可生成海报。 点击代码直接生成各种语言 SDK 的调用代码,方便快速开发。 软件特性&…...

力扣每日一题 6/28 动态规划/数组
博客主页:誓则盟约系列专栏:IT竞赛 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ 2742.给墙壁刷油漆【困难】 题目: 给你两个长度为 n 下标从 0…...

[数据集][目标检测]游泳者溺水检测数据集VOC+YOLO格式8275张4类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):8275 标注数量(xml文件个数):8275 标注数量(txt文件个数):8275 标注…...
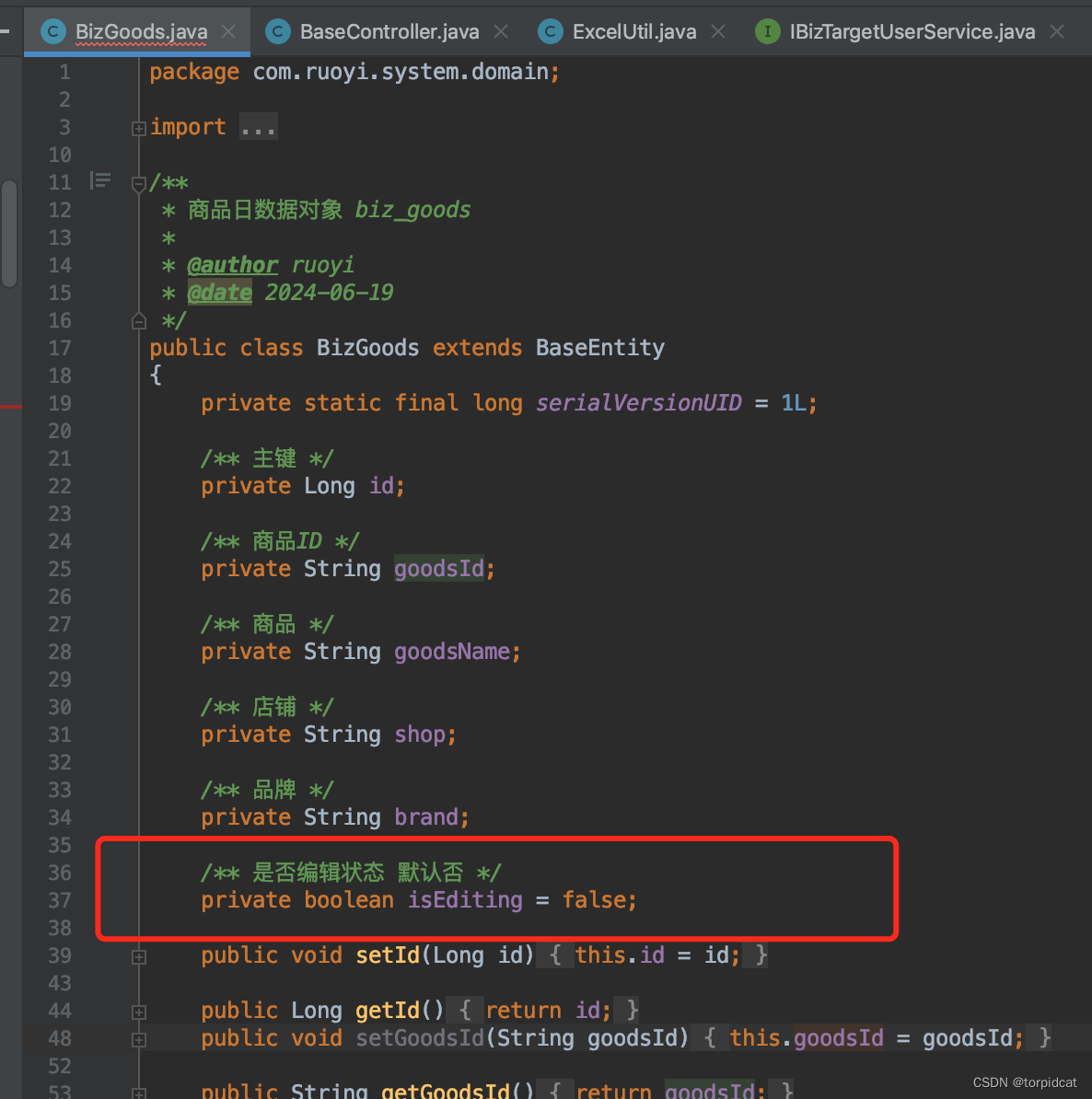
若依 ruoyi 分离版 vue 简单的行内编辑实现
需要实现的效果:双击文本 - 修改文本 - 保存修改。 原码:仅文本显示文字内容 <el-table-column label"商品" align"center" prop"goodsName" width"200" v-if"columns[1].visible" /> 实现…...

【工具】API文档生成DocFX
文章目录 总述示例第一步:安装 DocFX第二步:初始化项目第三步:编辑配置文件第四步:编写文档第五步:生成文档第六步:预览文档第七步:部署文档 总述 DocFX 是一个由微软开发的开源文档生成工具&a…...

在 JavaScript 中处理异步操作和临时事件处理程序
关键技术和设计总结 使用 Promise 和 then 进行异步操作: 我们通过使用 Promise 来处理异步操作,确保操作按顺序执行。在 getReportListByCurrentTime 函数中,返回一个 Promise 对象,保证在数据加载完成后调用 resolve,以便可以在…...
)
[Cocos Creator] v3.8开发知识点记录(持续更新)
问题:从 cc 里找不到宏定义 CC_PREVIEW 等。 解决方案:找不到就自己定义,将 declare const CC_PREVIEW; 添加到需要的ts文件里。参考:creator3d 找不到宏定义如 CC_EDITOR,CC_PREVIEW,CC_JSB - Creator 3.x…...

Excel_VBA编程
在Excel中,VBA(Visual Basic for Applications)是一种强大的工具,可以用来自动化各种任务。下面介绍一些常用的VBA函数和程序结构: 常用函数 MsgBox:用于显示消息框。 MsgBox "Hello, World!"In…...

Java中的Path类使用详解及最佳实践
Java中的Path类使用详解及最佳实践 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将深入探讨Java中的Path类,这是Java标准库中用于操作文件…...

生成和查看预定义宏
参考下面的指令 arm-none-eabi-gcc -marcharmv7e-m -dM -E - < /dev/null | grep SYNC这个指令是用来生成和查看预定义宏(macros)的一种方法。让我们逐步分解和解释这个命令的各个部分: arm-none-eabi-gcc: 这是 ARM 架构下的交叉编译器…...
)
Redis 7.x 系列【12】数据类型之基数统计(HyperLogLog)
有道无术,术尚可求,有术无道,止于术。 本系列Redis 版本 7.2.5 源码地址:https://gitee.com/pearl-organization/study-redis-demo 文章目录 1. 概述2. 常用命令2.1 PFADD2.2 PFCOUNT2.3 PFMERGE 3. 应用场景 1. 概述 基数表示数…...
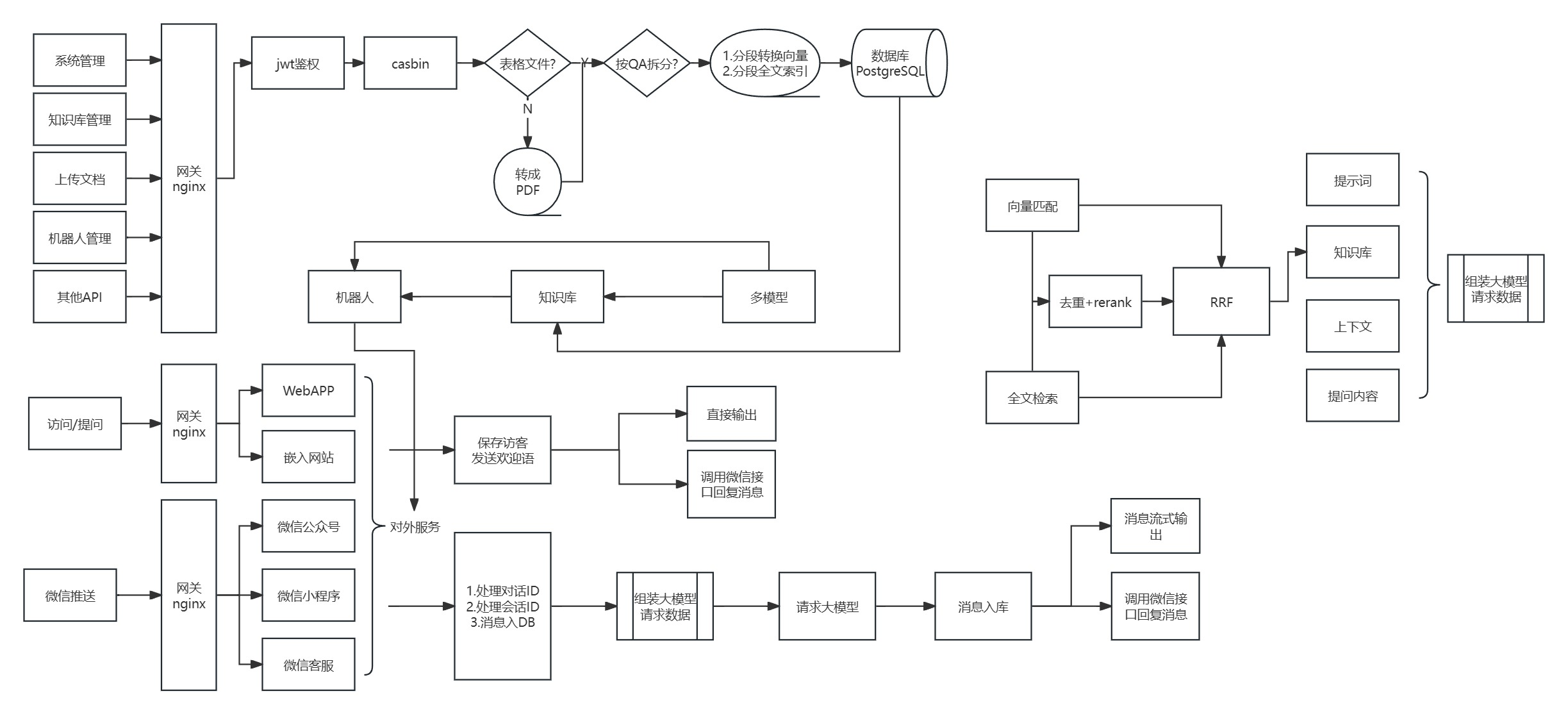
开源大模型RAG企业本地知识库问答机器人-ChatWiki
ChatWiki ChatWiki是一款开源的知识库 AI 问答系统。系统基于大语言模型(LLM )和检索增强生成(RAG)技术构建,提供开箱即用的数据处理、模型调用等能力,可以帮助企业快速搭建自己的知识库 AI 问答系统。 开…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
