【牛客】牛客小白月赛97 题解 A - E
文章目录
- A - 三角形
- B - 好数组
- C - 前缀平方和序列
- D - 走一个大整数迷宫
- E - 前缀和前缀最大值
A - 三角形
map存一下每个数出现了多少次,再遍历map
#include <bits/stdc++.h>using namespace std;#define int long long
using i64 = long long;typedef pair<int, int> PII;
typedef pair<int, char> PIC;
typedef pair<double, double> PDD;
typedef pair<int, PII> PIII;
typedef pair<int, pair<int, bool>> PIIB;const int N = 1e5 + 10;
const int maxn = 1e6 + 10;
const int mod = 998244353;
const int mod1 = 954169327;
const int mod2 = 906097321;
const int INF = 0x3f3f3f3f3f3f3f3f;void solve()
{int n;cin >> n;map<int, int> mp;for (int i = 0; i < n; i ++ ){int x; cin >> x;mp[x] ++ ;}for (auto t : mp){if (t.second >= 3){cout << "YES\n";return;}}cout << "NO\n";return;
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t = 1;
// cin >> t;while (t--){solve();}
}
B - 好数组
数组没有 0 就是好数组
#include <bits/stdc++.h>using namespace std;#define int long long
using i64 = long long;typedef pair<int, int> PII;
typedef pair<int, char> PIC;
typedef pair<double, double> PDD;
typedef pair<int, PII> PIII;
typedef pair<int, pair<int, bool>> PIIB;const int N = 1e5 + 10;
const int maxn = 1e6 + 10;
const int mod = 998244353;
const int mod1 = 954169327;
const int mod2 = 906097321;
const int INF = 0x3f3f3f3f3f3f3f3f;void solve()
{int n;cin >> n;vector<int> a(n + 1);for (int i = 1; i <= n; i ++ ) cin >> a[i];for (int i = 1; i <= n; i ++ ){if (a[i] == 0){cout << "NO\n";return;}}cout << "YES\n";
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t = 1;// cin >> t;while (t--){solve();}
}
C - 前缀平方和序列
对 x 开方,得到的就是能存在数组里的所有数的个数,我们要取 n 个,也就是 C(sqrt(x), n)
#include <bits/stdc++.h>using namespace std;#define int long long
using i64 = long long;typedef pair<int, int> PII;
typedef pair<int, char> PIC;
typedef pair<double, double> PDD;
typedef pair<int, PII> PIII;
typedef pair<int, pair<int, bool>> PIIB;const int N = 1e5 + 10;
const int maxn = 1e6 + 10;
const int mod = 1e9 + 7;
const int mod1 = 954169327;
const int mod2 = 906097321;
const int INF = 0x3f3f3f3f3f3f3f3f;int Jc[maxn + 1];void calJc() //求 maxn 以内的数的阶乘 不知道开多少就1e6吧爆不了
{Jc[0] = Jc[1] = 1;for(int i = 2; i < maxn; i++) Jc[i] = Jc[i - 1] * i % mod;
}int pow(int a, int n, int p) // 快速幂取模
{int ans = 1;while (n){if (n & 1) ans = ans * a % p;a = a * a % p;n >>= 1;}return ans;
}int niYuan(int a, int b) //费马小定理求逆元
{return pow(a, b - 2, b);
}int C(int a, int b) // 组合数
{if(a < b) return 0;return Jc[a] * niYuan(Jc[b], mod) % mod * niYuan(Jc[a - b], mod) % mod;
}void solve()
{calJc();int n, x;cin >> n >> x;int cnt = sqrt(x);int ans = C(cnt, n);cout << ans << '\n';
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t = 1;// cin >> t;while (t--){solve();}
}
D - 走一个大整数迷宫
首先需要注意到 c 的值和 b 一点关系都没有,因为 b 不可能对 (p - 1) 有任何贡献
明确这一点之后只需要 bfs 就可以了,注意需要判断 st[x][y][k] 不重复,(x, y) 就是点坐标,k 就是到达该点的余数
#include <bits/stdc++.h>using namespace std;#define int long long
using i64 = long long;typedef pair<int, int> PII;
typedef pair<int, char> PIC;
typedef pair<double, double> PDD;
typedef pair<int, PII> PIII;
typedef pair<int, pair<int, bool>> PIIB;const int N = 1e5 + 10;
const int maxn = 1e6 + 10;
const int mod = 1e9 + 7;
const int mod1 = 954169327;
const int mod2 = 906097321;
const int INF = 0x3f3f3f3f3f3f3f3f;int dx[4] = {0, 0, 1, -1}, dy[4] = {1, -1, 0, 0};struct node {int dist, res, x, y;
};void solve()
{int n, m, p;cin >> n >> m >> p;vector<vector<int>> a(n + 1, vector<int>(m + 1)), b(n + 1, vector<int>(m + 1));for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )cin >> a[i][j];for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )cin >> b[i][j];int ans = INF;queue<struct node> q;q.push({0, a[1][1] % (p - 1), 1, 1});vector<vector<vector<bool>>> st(n + 1, vector<vector<bool>>(m + 1, vector<bool>(p + 1)));while (q.size()){auto t = q.front();q.pop();if (st[t.x][t.y][t.res]) continue;st[t.x][t.y][t.res] = true;if (t.x == n && t.y == m && t.res % (p - 1) == 0){cout << t.dist << '\n';return;}if (t.dist >= 1e6){cout << -1 << '\n';return;}for (int i = 0; i < 4; i ++ ){int nx = t.x + dx[i], ny = t.y + dy[i];if (nx <= 0 || nx > n || ny <= 0 || ny > m) continue;q.push({t.dist + 1, (t.res + a[nx][ny]) % (p - 1), nx, ny});}}
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t = 1;// cin >> t;while (t--){solve();}
}
E - 前缀和前缀最大值
a 的前缀最大值数量最多的情况就是把正数全都排在前面的时候,此时数量为 正数个数+1,加的 1 代表最前面的前缀和 0
数量最少的情况就是把负数全都排在正数前面,且正数从小到大排列,这种情况怎么计算呢,因为 b 的值域最大只有100,所以用 cnt_pos[i][j] 表示前 i 个元素中 j 出现的次数,之后计算最多需要多少个正数可以把负数都抵消即可
答案就是最大值-最小值+1
#include <bits/stdc++.h>using namespace std;#define int long long
using i64 = long long;typedef pair<int, int> PII;
typedef pair<int, char> PIC;
typedef pair<double, double> PDD;
typedef pair<int, PII> PIII;
typedef pair<int, pair<int, bool>> PIIB;const int N = 10;
const int maxn = 1e6 + 10;
const int mod = 998244353;
const int mod1 = 954169327;
const int mod2 = 906097321;
const int INF = 0x3f3f3f3f3f3f3f3f;void solve()
{int n;cin >> n;vector<int> a(n + 1), pre_neg(n + 1);vector<vector<int>> cnt_pos(n + 1, vector<int>(110));for (int i = 1; i <= n; i ++ ){cin >> a[i];pre_neg[i] = pre_neg[i - 1] - min(a[i], (i64)0);for (int j = 1; j <= 100; j ++ ){cnt_pos[i][j] = cnt_pos[i - 1][j] + (a[i] == j);}} int q;cin >> q;while (q -- ){int l, r;cin >> l >> r;int cnt_plus = 0; // 正数个数for (int i = 1; i <= 100; i ++ ) cnt_plus += cnt_pos[r][i] - cnt_pos[l - 1][i];int sum_tmp = 0; // 当前正数之和int cnt_need = 0; // 需要多少正数和负数抵消for (int i = 1; i <= 100; i ++ ){int cnt = cnt_pos[r][i] - cnt_pos[l - 1][i];if (sum_tmp + i * cnt >= (pre_neg[r] - pre_neg[l - 1])){cnt_need += (pre_neg[r] - pre_neg[l - 1] - sum_tmp) / i;break;}else{cnt_need += cnt;sum_tmp += cnt * i;}}cout << cnt_plus + 1 - (cnt_plus - cnt_need + 1) + 1 << '\n';}
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t = 1;// cin >> t;while (t--){solve();}
}
相关文章:

【牛客】牛客小白月赛97 题解 A - E
文章目录 A - 三角形B - 好数组C - 前缀平方和序列D - 走一个大整数迷宫E - 前缀和前缀最大值 A - 三角形 map存一下每个数出现了多少次,再遍历map #include <bits/stdc.h>using namespace std;#define int long long using i64 long long;typedef pair<…...

Spring Boot中泛型参数的灵活运用:最佳实践与性能优化
泛型是Java中一种强大的特性,它提供了编写通用代码的能力,使得代码更加灵活和可复用。在Spring Boot应用程序中,泛型参数的灵活运用可以带来诸多好处,包括增强代码的可读性、提高系统的健壮性以及优化系统的性能。本文将深入探讨在…...

MySQL建表时的注意事项
以下是我对MySQL建表时的注意事项。其实,建表事项有很多,我的总结如下: 1 存储引擎的选择,一般做开发,都是要支持事务的,所以选择InnoDB 2 对字段类型的选择: 对于日期类型如果要记录时分…...
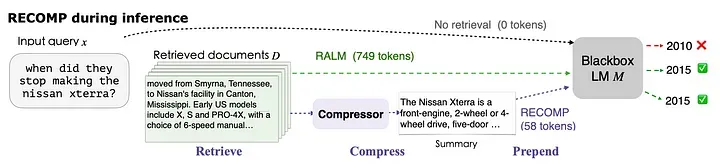
Advanced RAG 09:『提示词压缩』技术综述
编者按: 如何最大限度地发挥 LLMs 的强大能力,同时还能控制其推理成本?这是当前业界研究的一个热点课题。 针对这一问题,本期精心选取了一篇关于"提示词压缩"(Prompt Compression)技术的综述文章。正如作者所说…...
DroneCAN 适配器节点(二))
(13)DroneCAN 适配器节点(二)
文章目录 前言 2 固件 2.1 基于F103 2.2 基于F303 2.3 基于F431 3 ArduPilot固件DroneCAN设置 3.1 f303-通用设置示例 4 DroneCAN适配器节点 前言 这些节点允许现有的 ArduPilot 支持的外围设备作为 DroneCAN 或 MSP 设备适应 CAN 总线。这也允许扩展自动驾驶仪硬件的…...
摸鱼大数据——Spark基础——Spark环境安装——Spark Local[*]搭建
一、虚拟机配置 查看每一台的虚拟机的IP地址和网关地址 查看路径: cat /etc/sysconfig/network-scripts/ifcfg-ens33 2.修改 VMware的网络地址: 使用VMnet8 3.修改windows的对应VMware的网卡地址 4.通过finalshell 或者其他的shell连接工具即可连接使用即可, 连接后, 测试一…...
)
函数内部结构分层浅析(从MVC分层架构联想)
函数内部结构分层浅析(从MVC分层架构联想) 分层架构:一种将软件代码按不同功能进行划分的架构模式。 优点包括: 可维护性:各层职责明确,易于单独修改维护。 可扩展性:方便添加或修改某一层,不…...

【three.js案例二】时空隧道
import * as THREE from ./build/three.module.js // 引入轨道控制器扩展库OrbitControls.js import { OrbitControls } from three/addons/controls/OrbitControls.js; // 引入dat.gui.js的一个类GUI import { GUI } from three/addons/libs/lil-gui.module.min.js;// 场景 co…...

动手学深度学习(Pytorch版)代码实践 -计算机视觉-48全连接卷积神经网络(FCN)
48全连接卷积神经网络(FCN) 1.构造函数 import torch import torchvision from torch import nn from torch.nn import functional as F import matplotlib.pyplot as plt import liliPytorch as lp from d2l import torch as d2l# 构造模型 pretrained…...

【Python游戏】猫和老鼠
本文收录于 《一起学Python趣味编程》专栏,从零基础开始,分享一些Python编程知识,欢迎关注,谢谢! 文章目录 一、前言二、代码示例三、知识点梳理四、总结一、前言 本文介绍如何使用Python的海龟画图工具turtle,开发猫和老鼠游戏。 什么是Python? Python是由荷兰人吉多范…...

【无标题】c# WEBAPI 读写表到Redis
//c# WEBAPI 读写表到Redis using System; using System.Collections.Generic; using System.Linq; using System.Net; using System.Net.Http; using System.Web.Http; using Newtonsoft.Json; using StackExchange.Redis; using System.Data; using System.Web; namespace …...
)
【剑指Offer系列】53-0到n中缺失的数字(index)
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。 示例 1: 输入:nums [3,0,1] 输出:2 解释:n 3,因为有 3 个数字,所以所有的数字都在范围 [0,3]…...

docker compose部署zabbix7.0官方方法快速搭建
环境介绍: 系统:centos7 官方文档:https://www.zabbix.com/documentation/current/zh/manual/installation/containers docker镜像加速 vi /etc/docker/daemon.json{"registry-mirrors": ["https://docker.1panel.live&quo…...
?)
分库分表之后如何设计主键ID(分布式ID)?
文章目录 1、数据库的自增序列步长方案2、分表键结合自增序列3、UUID4、雪花算法5、redis的incr方案总结 在进行数据库的分库分表操作后,必然要面临的一个问题就是主键id如何生成,一定是需要一个全局的id来支持,所以分库分表之后,…...
秋招突击——6/28、6.29——复习{数位DP——度的数量}——新作{}
文章目录 引言复习数位DP——度的数量个人实现参考实现 总结 引言 头一次产生了那么强烈的动摇,对于未来没有任何的感觉的,不知道将会往哪里走,不知道怎么办。可能还是因为实习吧,再加上最近复习也没有什么进展,并不知…...

Spring Boot中使用Thymeleaf进行页面渲染
Spring Boot中使用Thymeleaf进行页面渲染 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将探讨如何在Spring Boot应用中使用Thymeleaf模板引擎进行页面…...

恢复策略(下)-事务故障后的数据库恢复、系统故障后的数据库恢复(检查点技术)、介质故障后的数据库恢复
一、数据库恢复-事务故障 系统通过对事物进行UNDO操作和REDO操作可实现故障后的数据库状态恢复 1、对于发生事务故障后的数据库恢复 恢复机制在不影响其他事务运行的情况下,强行回滚夭折事务,对该事务进行UNDO操作,来撤销该事务已对数据库…...

如何知道docker谁占用的显卡的显存?
文章目录 python环境安装nvidia-htop查看pid加一个追踪总结一下【找到容器创建时间】使用说明示例 再总结一下【用PID找到容器创建时间,从而找到谁创建的】使用说明示例 python环境安装nvidia-htop nvidia-htop是一个看详细的工具。 pip3 install nvidia-htop查看…...
wps linux node.js 加载项开发,和离线部署方案
环境准备 windwos 安装node.js 安装VSCode 安装wps linux 安装node.js 安装VSCode 安装wps 通过npm 安装wpsjs SDK 使用npm安装wpsjs npm install -g wpsjs 创建一个项目 wpsjs create WPS-Addin-PPT 创建项目会让你选择2个东西: 1:选择你的文…...
红队内网攻防渗透:内网渗透之内网对抗:横向移动篇Kerberos委派安全非约束系约束系RBCD资源系Spooler利用
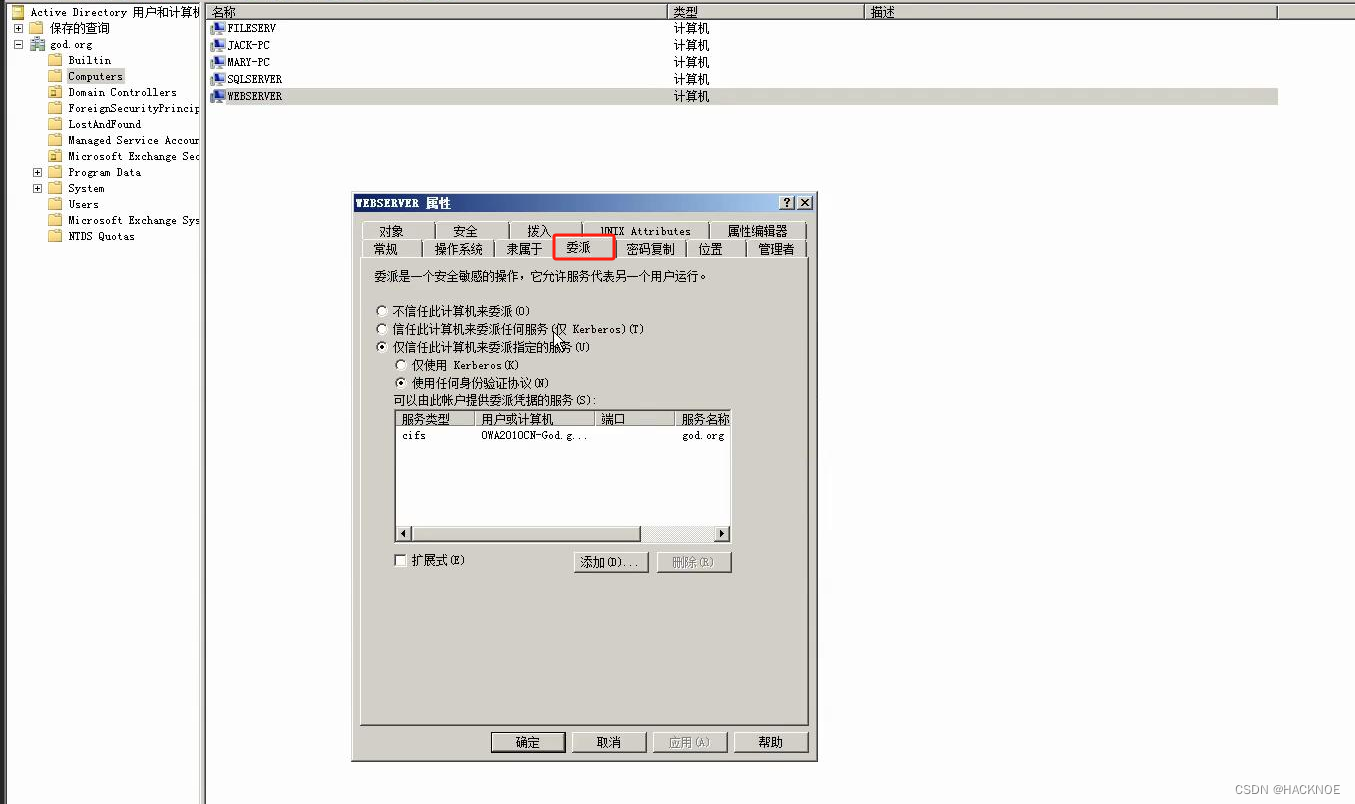
红队内网攻防渗透 1. 内网横向移动1.1 委派安全知识点1.1.1 域委派分类1.1.2 非约束委派1.1.2.1 利用场景1.1.2.2 复现配置:1.1.2.3 利用思路1:诱使域管理员访问机器1.1.2.3.1 利用过程:主动通讯1.1.2.3.2 利用过程:钓鱼1.1.2.4 利用思路2:强制结合打印机漏洞1.1.2.5 利用…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...
