狄克斯特拉算法
狄克斯特拉算法(Dijkstra’s algorithm)是一种用于在带权图中找到从单一源点到所有其他顶点的最短路径的算法。它适用于处理带有非负权值的图。
下面将详细解释算法的工作原理、时间复杂度以及如何通过优化数据结构来改进其性能。
狄克斯特拉算法的工作原理
-
初始化:算法开始时,将所有顶点标记为未访问。源点到自身的距离设为0,其他所有顶点到源点的距离设为无穷大(表示尚未找到路径)。
-
选择最小距离顶点:在未访问的顶点中,选择一个具有最小距离的顶点,称为当前顶点。
-
松弛操作:对于当前顶点的每一个邻接顶点,执行松弛操作。如果通过当前顶点到邻接顶点的路径比已知的路径更短,则更新该邻接顶点的距离。
-
标记访问:将当前顶点标记为已访问,然后从未访问顶点集合中移除。
-
重复迭代:重复步骤2到4,直到所有顶点都被访问或者找到目标顶点。
时间复杂度分析
-
原始算法:在每次迭代中,算法需要从所有未访问的顶点中选择一个最小距离的顶点,这需要 O(n) 的时间。由于有 n 个顶点,因此总的时间复杂度是 O(n^2)。
-
优化后的算法:通过使用优先队列(如二叉堆或斐波那契堆),算法可以在 O(log n) 的时间内找到最小距离的顶点。更新邻接顶点的距离并将其重新插入优先队列也需要 O(log n) 的时间。因此,对于每个顶点的松弛操作,总时间复杂度是 O(n log n)。由于有 m 条边,每个边可能需要进行一次松弛操作,所以边的松弛操作总时间复杂度是 O(m log n)。综合考虑,优化后的算法时间复杂度是 O((n + m) log n)。
数据结构优化
-
优先队列:使用优先队列可以快速访问最小元素,并且可以在对数时间内插入和删除元素。这是优化狄克斯特拉算法的关键。
-
二叉堆:一种常见的实现优先队列的数据结构,但在最坏情况下,插入和删除操作的时间复杂度为 O(log n)。
-
斐波那契堆:另一种实现优先队列的数据结构,它在平均情况下可以提供更好的性能,特别是在删除最小元素时,平均时间复杂度接近 O(1)。
实际应用中的注意事项
-
图的表示:图可以以邻接矩阵或邻接表的形式表示。邻接矩阵适用于稠密图,而邻接表适用于稀疏图。
-
负权边:狄克斯特拉算法不适用于包含负权边的图。对于这种情况,可以使用贝尔曼-福特算法。
-
算法变体:存在狄克斯特拉算法的变体,如 A* 搜索算法,它使用启发式信息来进一步优化搜索过程。
代码实现
使用数组实现的Dijkstra算法
package mainimport "math"type Graph struct {vertices int // 图中顶点的数量edges [][]int // 存储边权重的邻接表
}// NewGraph 创建一个新的图实例
func NewGraph(v int) *Graph {return &Graph{vertices: v,edges: make([][]int, v),}
}// DijkstraArray 使用数组实现的Dijkstra算法来计算从源顶点到所有其他顶点的最短路径
func (g *Graph) DijkstraArray(src int) []int {dist := make([]int, g.vertices) // 存储从源顶点到每个顶点的最短距离visited := make([]bool, g.vertices) // 记录顶点是否已经被访问过// 初始化距离数组,所有顶点距离设为无穷大for i := range dist {dist[i] = math.MaxInt32}dist[src] = 0 // 源顶点到自身的距离设为0// 找到最短距离的顶点进行迭代更新for count := 0; count < g.vertices-1; count++ {u := g.minDistance(dist, visited) // 从未访问过的顶点中找到距离最小的顶点visited[u] = true // 标记顶点u为已访问// 更新顶点u的邻接顶点的最短距离for v := 0; v < g.vertices; v++ {if !visited[v] && g.edges[u][v] != 0 && dist[u]+g.edges[u][v] < dist[v] {dist[v] = dist[u] + g.edges[u][v]}}}return dist // 返回从源顶点到所有其他顶点的最短距离数组
}// minDistance 辅助函数,找到当前距离数组中距离最小的顶点
func (g *Graph) minDistance(dist []int, visited []bool) int {min := math.MaxInt32minIndex := -1for v := range dist {if !visited[v] && dist[v] <= min {min = dist[v]minIndex = v}}return minIndex
}func main() {g := NewGraph(9)g.edges = [][]int{{0, 4, 0, 0, 0, 0, 0, 8, 0},{4, 0, 8, 0, 0, 0, 0, 11, 0},{0, 8, 0, 7, 0, 4, 0, 0, 2},{0, 0, 7, 0, 9, 14, 0, 0, 0},{0, 0, 0, 9, 0, 10, 0, 0, 0},{0, 0, 4, 14, 10, 0, 2, 0, 0},{0, 0, 0, 0, 0, 2, 0, 1, 6},{8, 11, 0, 0, 0, 0, 1, 0, 7},{0, 0, 2, 0, 0, 0, 6, 7, 0},}distances := g.DijkstraArray(0)println("Shortest distances from source vertex 0:")for i, dist := range distances {println(i, ":", dist)}
}
使用最小堆实现优先级队列的Dijkstra算法
package main import ( "container/heap" "fmt" "math"
) // Item 是优先级队列中的元素,包含顶点和其距离
type Item struct { vertex int // 顶点 dist int // 顶点的当前距离 index int // 顶点在dist数组中的索引(可选,用于更新)
} // PriorityQueue 是优先级队列,基于Item的dist字段排序
type PriorityQueue []*Item func (pq PriorityQueue) Len() int { return len(pq) } func (pq PriorityQueue) Less(i, j int) bool { return pq[i].dist < pq[j].dist
} func (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] pq[i].index = i pq[j].index = j
} func (pq *PriorityQueue) Push(x interface{}) { n := len(*pq) item := x.(*Item) item.index = n *pq = append(*pq, item)
} func (pq *PriorityQueue) Pop() interface{} { old := *pq n := len(old) item := old[n-1] item.index = -1 // for safety *pq = old[0 : n-1] return item
} func (pq *PriorityQueue) update(item *Item, dist int) { item.dist = dist heap.Fix(pq, item.index)
} // Edge 表示图中的一条边
type Edge struct { to int // 目标顶点 weight int // 边的权重
} // Graph 表示整个图结构
type Graph struct { vertices int // 图中顶点的数量 edges [][]*Edge // 存储边的邻接表,使用指针避免复制
} // DijkstraMinHeap 使用最小堆优先级队列的Dijkstra算法
func (g *Graph) DijkstraMinHeap(src int) []int { dist := make([]int, g.vertices) for i := range dist { dist[i] = math.MaxInt32 } dist[src] = 0 pq := make(PriorityQueue, 0) heap.Init(&pq) heap.Push(&pq, &Item{vertex: src, dist: 0}) for pq.Len() > 0 { item := heap.Pop(&pq).(*Item) u := item.vertex for _, edge := range g.edges[u] { v := edge.to alt := dist[u] + edge.weight if alt < dist[v] { dist[v] = alt heap.Push(&pq, &Item{vertex: v, dist: alt}) } } } return dist
} func main() { // 初始化图的边的连接关系 graph := Graph{ vertices: 9, edges: [][]*Edge{ {{to: 1, weight: 4}, {to: 7, weight: 8}}, {{to: 0, weight: 4}, {to: 2, weight: 8}, {to: 7, weight: 11}}, {{to: 1, weight: 8}, {to: 3, weight: 7}, {to: 5, weight: 4}, {to: 8, weight: 2}}, {{to: 2, weight: 7}, {to: 4, weight: 9}, {to: 5, weight: 14}}, {{to: 3, weight: 9}, {to: 5, weight: 10}}, {{to: 2, weight: 4}, {to: 3, weight: 14}, {to: 4, weight: 10}, {to: 6, weight: 2}}, {{to: 5, weight: 2}, {to: 7, weight: 1}, {to: 8, weight: 6}}, {{to: 0, weight: 8}, {to: 1, weight: 11}, {to: 6, weight: 1}, {to: 8, weight: 7}}, {{to: 2, weight: 2}, {to: 6, weight: 6}, {to: 7, weight: 7}}, }, } distances := graph.DijkstraMinHeap(0)fmt.Println("Shortest distances from source vertex 0:")for i, dist := range distances {fmt.Printf("%d: %d\n", i, dist)}
}
相关文章:

狄克斯特拉算法
狄克斯特拉算法(Dijkstra’s algorithm)是一种用于在带权图中找到从单一源点到所有其他顶点的最短路径的算法。它适用于处理带有非负权值的图。 下面将详细解释算法的工作原理、时间复杂度以及如何通过优化数据结构来改进其性能。 狄克斯特拉算法的工作…...

2024推荐整理几个磁力导航网站可提供海量资源的
都2024现在网上找资源像流水得鱼一样,抓一大把结果很难吃,我通宵特意整理的网站,网上有许多磁力导航网站可以提供海量的磁力链接资源,以下是一些有效的磁力导航网站推荐: 磁力搜索 链接: 资源类型&#x…...

链式访问:C语言中的函数调用技巧
链式访问:C语言中的函数调用技巧 在C语言编程中,链式访问(chained calls)是一个常见的编程技巧,它允许你在一行代码中连续调用多个函数或方法。这种技巧不仅能够让代码更加简洁和易读,还能减少临时变量的使…...
-1个手机号多用户身份)
数据库设计(实战项目)-1个手机号多用户身份
一. 背景: 该需求是一个互联网医院的预约单场景,护士在小程序上申请患者查房预约单,医生在小程序上对预约单进行接单,护士开始查房后填写查房小结,客户需要对用户信息进行授权,医生查房后进行签字ÿ…...

vue+fineReport 使用前端搜索+报表显示数据
--fineReprot 将需要搜索的参数添加到模版参数 sql: --前端传递参数 注:因为每次点击搜索的结果需要不一样,还要传递一个时间戳的参数: let timesamp new Date().getTime()...

高阶面试-存储系统的设计
概述 分类 块存储 block storage文件存储 file storage对象存储 object storage 区别: 块存储 概述 位于最底层,块,是物理存储设备上数据存储的最小单位。硬盘(Hard Disk Drive,HDD)就属于块存储。常见的还有固态硬盘(SSD)、…...

柔性测斜仪:土木工程与地质监测的得力助手
在现代土木工程和地质工程领域,精确监测土壤和岩石的位移情况对于确保工程安全至关重要。柔性测斜仪作为一种高精度、稳定性和灵活性兼备的测量设备,已逐渐成为工程师和研究人员的得力助手。本文将深入探讨柔性测斜仪在多个关键领域的应用及其重要性。 点…...

数字资产和数据资产你真的了解吗?
数据作为新型生产要素,是数字化、网络化、智能化的基础,已快速融入生产、分配、流通、消费和社会服务管理等各环节,深刻改变着生产方式、生活方式和社会治理方式。 何为数据资产?即由个人或企业拥有或控制的,能为企业带…...
【每日一练】python运算符
1. 算术运算符 编写一个Python程序,要求用户输入两个数,并执行以下运算:加法、减法、乘法、求余、除法、以及第一个数的第二个数次方。将结果打印出来。 a input("请输入第一个数:") b input("请输入第二个数&…...
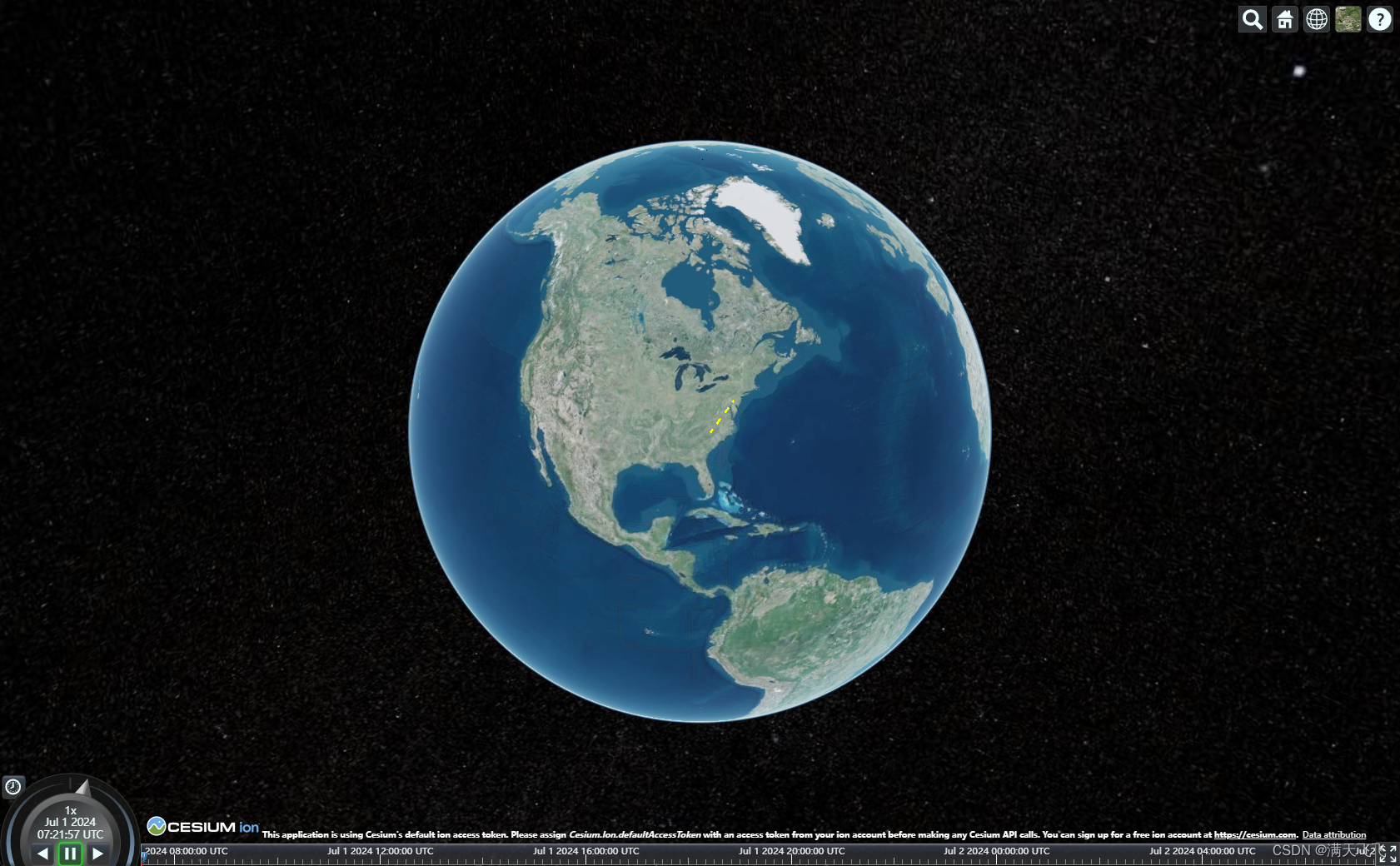
CesiumJS【Basic】- #032 绘制虚线(Primitive方式)
文章目录 绘制虚线(Primitive方式)1 目标2 代码2.1 main.ts绘制虚线(Primitive方式) 1 目标 使用Primitive方式绘制虚线 2 代码 2.1 main.ts // 定义线条的起点和终点var start = Cesium.Cartesian3.fromDegrees(-75.59777, 40.03883)...

海尔智家:科技优秀是一种习惯
海尔智家:科技优秀是一种习惯 2024-06-28 15:19代锡海 6月24日,2023年度国家科学技术奖正式揭晓。海尔智家“温湿氧磁多维精准控制家用保鲜电器技术创新与产业化”项目荣获国家科学技术进步奖,成为家电行业唯一牵头获奖企业。 很多人说&…...
【Android】实现图片和视频混合轮播(无限循环、视频自动播放)
目录 前言一、实现效果二、具体实现1. 导入依赖2. 布局3. Banner基础配置4. Banner无限循环机制5. 轮播适配器6. 视频播放处理7. 完整源码 总结 前言 我们日常的需求基本上都是图片的轮播,而在一些特殊需求,例如用于展览的的数据大屏,又想展…...

VLAN基础
一、什么是Vlan VLAN(Virtual Local Area Network)是虚拟局域网的简称,是一种将单一物理局域网(LAN)在逻辑层面上划分为多个独立的广播域的技术。每个VLAN都是一个独立的广播域,其内部主机可以直接通信&am…...

pytest-yaml-sanmu(五):跳过执行和预期失败
除了手动注册标记之外,pytest 还内置了一些标记可直接使用,每种内置标记都会用例带来不同的特殊效果,本文先介绍 3 种。 1. skip skip 标记通常用于忽略暂时无法执行,或不需要执行的用例。 pytest 在执行用例时,如果…...
)
linux指令整合(centos系统持续更新中。。。)
1、查询java进程 ps -ef|grep java 2、查询端口占用 lsof -i:端口号 3、 启动java程序 java -jar jar包路径 后台启动 nohup java -jar jar包路径 -Xms512m -Xmx512m > 日志路径 2>&1 & 4、查看服务器资源占用 top 5、关闭进程 kill -9 进程号...

个人开发实现AI套壳网站快速搭建(Vue+elementUI+SpringBoot)
目录 一、效果展示 二、项目概述 三、手把手快速搭建实现本项目 3.1 前端实现 3.2 后端方向 五、后续开发计划 一、效果展示 默认展示 一般对话展示: 代码对话展示: 二、项目概述 本项目是一个基于Web的智能对话服务平台,通过后端与第…...
Cesium与Three相机同步(3)
Cesium与Three融合的案例demo <!DOCTYPE html> <html lang"en" class"dark"><head><meta charset"UTF-8"><link rel"icon" href"/favicon.ico"><meta name"viewport" content&q…...

PMP考试报名项目经历怎么填写?指引请收好
PMP,这一全球公认的项目管理金牌认证,不仅是对项目管理能力的认可,更是职业生涯中的一大助力。然而,在报名PMP时,很多小伙伴都面临一个共同的难题:如何书写项目经验?今天,就让我们一…...

Git的基本使用方法
Git的基本使用方法 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将深入探讨Git的基本使用方法,Git作为目前最流行的版本控制系统之一&…...

深入剖析 @Autowired 和 @Resource 在 Spring 中的区别
在 Spring 框架中,Autowired 和 Resource 是两个常用的注解,用于实现依赖注入。尽管它们都能达到将依赖对象注入到目标 bean 的目的,但在细节上存在一些显著的差异。本文将深入探讨这两个注解的区别,并结合 Spring 源码进行分析&a…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
