滤波算法 | 无迹卡尔曼滤波(UKF)算法及其Python实现
文章目录
- 简介
- UKF滤波
- 1. 概述和流程
- 2. Python代码
- 第一个版本
- a. KF滤波
- b. UKF滤波
- 第二个版本
简介
上一篇文章,我们介绍了UKF滤波公式及其MATLAB代码。在做视觉测量的过程中,基于OpenCV的开发包比较多,因此我们将UKF的MATLAB代码转到python中,实现数据滤波效果。
UKF滤波
1. 概述和流程
UKF的公式这里就不再过多介绍了,具体内容请参见博客:UKF滤波公式及其MATLAB代码
这里简单把上一篇文章的公式和流程图粘贴一下。
求解流程 :
-
相比于一般的卡尔曼滤波,UKF算法增加了两次无迹变换,公式为:

权重和方差计算公式为:

-
Sigma点传播:

- 计算x的预测值和协方差矩阵:

4. 得到一组新的Sigma点:

5. 代入观测方程中,得到测量量的预估值:
![]()
- 获得观测量的预测值和协方差矩阵:

- 更新状态变量和协方差矩阵:



另外,每次写论文画卡尔曼流程图中,都找不到参考的模板。我自己画了个滤波流程图,不一定符合每个人的审美,以备参考:

2. Python代码
重点来了。。。
上代码。
第一个版本
UKF的python代码我一共写了两个版本。
第一个是我用ChatGPT直接生成了一个,经过数据实测,结果有点奇怪,不太像我想要的结果,每个模块之间的交互也跟我理解的不太一样。为了对比,这里也还是贴出来了,人家写的确实比我写的看着逼格好点。
ChatGPT输出的Python:
a. KF滤波
class KalmanFilter:def __init__(self, F, H, Q, R, P, x0):self.F = Fself.H = Hself.Q = Qself.R = Rself.P = Pself.x = x0def predict(self):self.x = self.F @ self.xself.P = self.F @ self.P @ self.F.T + self.Qdef update(self, z):y = z - self.H @ self.xS = self.H @ self.P @ self.H.T + self.RK = self.P @ self.H.T @ np.linalg.inv(S)self.x = self.x + K @ yself.P = (np.eye(len(self.x)) - K @ self.H) @ self.P
b. UKF滤波
import numpy as np
from scipy.linalg import sqrtmclass UKF:def __init__(self, f, h, Q, R, P, x0):self.f = fself.h = hself.Q = Qself.R = Rself.P = Pself.x = x0self.n = x0.shape[0]self.m = Nonedef predict(self):# Generate sigma pointsL = np.linalg.cholesky(self.P)W = np.concatenate((np.zeros((self.n, 1)), sqrtm(self.n * self.P)))X = np.concatenate((self.x, self.x + W, self.x - W), axis=1)# Predict sigma pointsY = np.zeros((self.n, 2 * self.n + 1))for i in range(2 * self.n + 1):Y[:, i] = self.f(X[:, i])# Compute mean and covarianceself.x = np.mean(Y, axis=1, keepdims=True)self.P = np.cov(Y) + self.Qdef update(self, z):# Generate sigma pointsL = np.linalg.cholesky(self.P)W = np.concatenate((np.zeros((self.n, 1)), sqrtm(self.n * self.P)))X = np.concatenate((self.x, self.x + W, self.x - W), axis=1)# Predict measurementsZ = np.zeros((self.m, 2 * self.n + 1))for i in range(2 * self.n + 1):Z[:, i] = self.h(X[:, i])# Compute mean and covariancez_mean = np.mean(Z, axis=1, keepdims=True)z_cov = np.cov(Z) + self.R# Compute cross-covariancexz_cov = np.zeros((self.n, self.m))for i in range(2 * self.n + 1):xz_cov += (X[:, i, np.newaxis] - self.x) @ (Z[:, i, np.newaxis] - z_mean).Txz_cov /= 2 * self.n# Compute Kalman gainK = xz_cov @ np.linalg.inv(z_cov)# Update estimateself.x += K @ (z - z_mean)self.P -= K @ z_cov @ K.T第二个版本
第二个是我自己改的一个。参考MATLAB的流程,直接改成了python代码,没有做代码的优化,结果还挺好的,和MATLAB结果一致。
import mathimport numpy as np
from scipy.linalg import sqrtmclass ukf:def __init__(self, f, h):self.f = fself.h = hself.Q = Noneself.R = Noneself.P = Noneself.x = Noneself.Z = Noneself.n = Noneself.m = Nonedef GetParameter(self, Q, R, P, x0):self.Q = Qself.R = Rself.P = Pself.x = x0self.n = x0.shape[0]self.m = Nonedef sigmas(self,x0, c):A = c * np.linalg.cholesky(self.P).TY = (self.x * np.ones((self.n,self.n))).TXset = np.concatenate((x0.reshape((-1,1)), Y+A, Y-A), axis=1)return Xsetdef ut1(self, Xsigma, Wm, Wc):LL = Xsigma.shape[1]Xmeans = np.zeros((self.n,1))Xsigma_pre = np.zeros((self.n, LL))for k in range(LL):Xsigma_pre[:,k] = self.f(Xsigma[:,k])Xmeans = Xmeans + Wm[0,k]* Xsigma_pre[:, k].reshape((self.n, 1))Xdiv = Xsigma_pre - np.tile(Xmeans,(1,LL))P = np.dot(np.dot(Xdiv, np.diag(Wc.reshape((LL,)))), Xdiv.T) + self.Qreturn Xmeans, Xsigma_pre, P, Xdivdef ut2(self, Xsigma, Wm, Wc, m):LL = Xsigma.shape[1]Xmeans = np.zeros((m, 1))Xsigma_pre = np.zeros((m, LL))for k in range(LL):Xsigma_pre[:, k] = self.h(Xsigma[:, k])Xmeans = Xmeans + Wm[0, k] * Xsigma_pre[:, k].reshape((m, 1))Xdiv = Xsigma_pre - np.tile(Xmeans, (1, LL))P = np.dot(np.dot(Xdiv, np.diag(Wc.reshape((LL,)))), Xdiv.T) + self.Rreturn Xmeans, Xsigma_pre, P, Xdivdef OutPutParameter(self, alpha_msm, x0, Q, R, P):z = np.array(alpha_msm).reshape((3, 1))self.GetParameter(Q, R, P, x0)l = self.nm = z.shape[0]alpha = 2ki = 3 - lbeta = 2lamb = alpha ** 2 * (l + ki) - lc = l + lambWm = np.concatenate((np.array(lamb / c).reshape((-1,1)), 0.5 / c + np.zeros((1, 2 * l))), axis=1)Wc = Wm.copy()Wc[0][0] = Wc[0][0] + (1 - alpha ** 2 + beta)c = math.sqrt(c)Xsigmaset = self.sigmas(x0, c)X1means, X1, P1, X2 = self.ut1(Xsigmaset, Wm, Wc)Zpre, Z1, Pzz, Z2 = self.ut2(X1, Wm, Wc, m)Pxz = np.dot(np.dot(X2 , np.diag(Wc.reshape((self.n*2+1,)))), Z2.T)K =np.dot(Pxz , np.linalg.inv(Pzz))X = (X1means + np.dot(K, z - Zpre)).reshape((-1,))self.P = P1 - np.dot(K , Pxz.T)return X, self.P这里把两个代码都公开出来,以供参考。
如有疑问,欢迎提问和指正。
相关文章:

滤波算法 | 无迹卡尔曼滤波(UKF)算法及其Python实现
文章目录简介UKF滤波1. 概述和流程2. Python代码第一个版本a. KF滤波b. UKF滤波第二个版本简介 上一篇文章,我们介绍了UKF滤波公式及其MATLAB代码。在做视觉测量的过程中,基于OpenCV的开发包比较多,因此我们将UKF的MATLAB代码转到python中&a…...

IMU 积分的误差状态空间方程推导
文章目录0. 前言1. 离散时间的IMU运动学方程2. 状态变量定义3. 补充公式4. IMU误差状态空间方程推导4.1. 旋转误差 δr^i1\delta\hat{\mathbf{r}}_{i1}δr^i14.2. 速度误差 δv^i1\delta\hat{\mathbf{v}}_{i1}δv^i14.3. 平移误差 δpi1\delta \mathbf{p}_{i1}δpi14.4. …...

VirtualBox的克隆与复制
快照太多,想整合成1个文件怎么办? 最近,我就遇到一个问题。快照太多了。比较占用空间怎么办? 错误做法 一开始,我是这么操作的,选中某个快照,然后选择删除…然后我登录虚拟机后,发…...

每天5分钟玩转机器学习算法:逆向概率的问题是什么?贝叶斯公式是如何解决的?
本文重点 前面我们已经知道了贝叶斯公式,以及贝叶斯公式在机器学习中的应用,那么贝叶斯公式究竟解决了一个什么样的问题呢?贝叶斯是为了解决逆向概率的问题。 正向的概率和逆向的概率 正向概率:假设袋子里面有N个白球,有M个黑球,你伸手一摸,那么问题就是你摸出黑球的概…...

游戏闲聊之游戏是怎么赚钱的
其实一般情况下不太爱写这种文章,简单说就一点,这个行业的人我惹不起。 1、外挂 所谓外挂,是指通过技术手段,提供辅助游戏的工具,方便玩家获得一些额外的能力; 这事我特意咨询过律师,外挂分两…...
Redis高频面试题汇总(下)
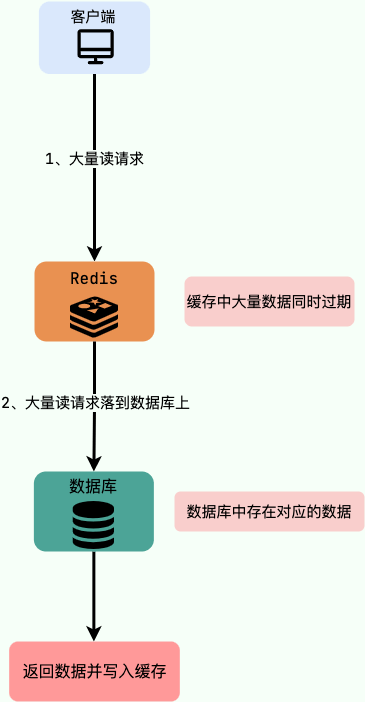
目录 1.Redis中什么是Big Key(大key) 2.Big Key会导致什么问题 3.如何发现 bigkey? 4.为什么redis生产环境慎用keys *命令 5.如何处理大量 key 集中过期问题 6.使用批量操作减少网络传输 7.缓存穿透 8.缓存击穿 9.缓存雪崩 10.缓存污染(或满了…...
Windows修改Docker安装目录修改Docker镜像目录,镜像默认存储位置存放到其它盘
Windows安装Docker,默认是安装在C盘,下载镜像后会占用大量空间,这时需要调整镜像目录;场景:不想连服务器或者没有服务器,想在本地调试服务,该需求就非常重要。基于WSL2安装docker后,…...

376. 摆动序列——【Leetcode每日刷题】
376. 摆动序列 如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。 例如, [1, 7, 4, 9, 2, 5] 是一个…...
mgre实验
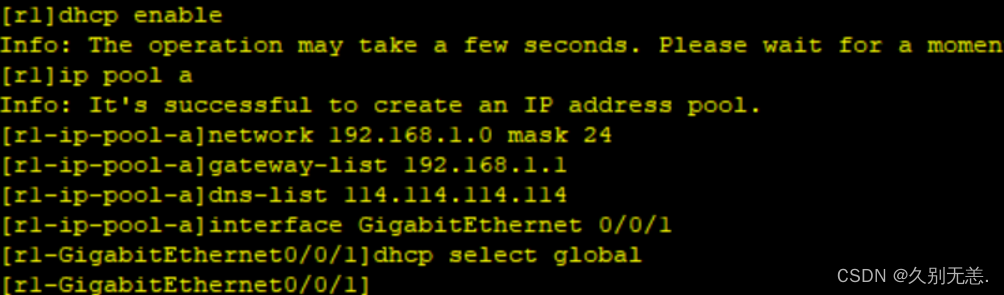
实验思路 1、首先根据拓扑结构合理分配IP地址,并对各个路由器的IP地址和R5环回接口的IP地址进行配置。 2、让私网中的边界路由器对ISP路由器做缺省路由。 3、根据实验要求,对需要配置不同类型认证的路由器进行认证配置,和需要不同封装的协议…...
)
一文彻底了解Zookeeper(介绍篇)
zookeeper 是什么? zookeeper是一个分布式协作框架,提供高可用,高性能,强一致等特性 zookeeper 有哪些应用场景? 分布式锁:分布式锁是指在分布式环境中,多个进程或线程需要互斥地访问某个共享…...
1. ELK Stack 理论篇之什么是ELK Stack?
ELK Stack 理论篇之什么是ELK Stack?1.1 什么是 ELK Stack?1.2 ELK Stack的发展史1.2.1 Elasticsearch1.2.2 引入 Logstash 和 Kibana,产品更强大1.2.3 社区越来越壮大,用例越来越丰富1.2.4 然后我们向 ELK 中加入了 Beats1.2.5 那么&#x…...
两道有关链表的练习
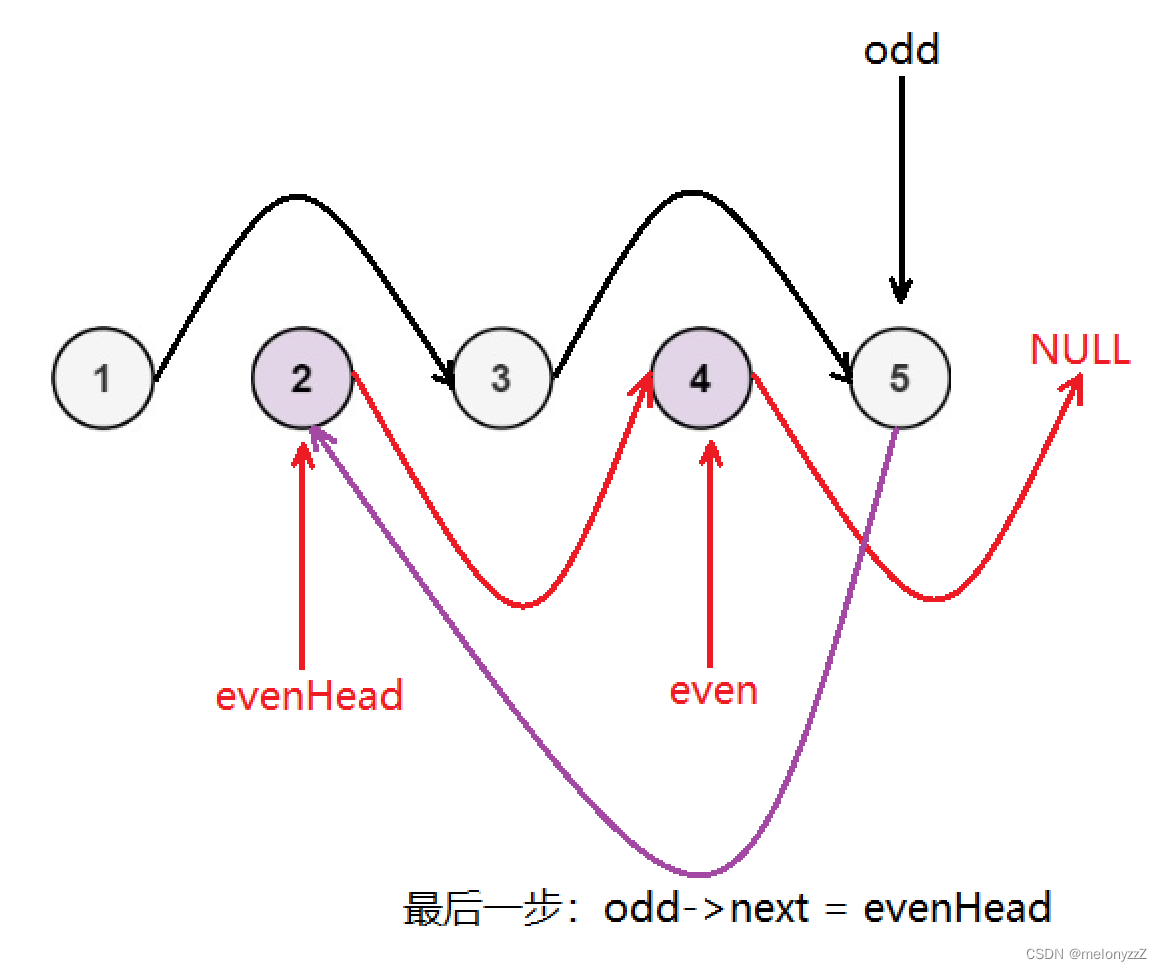
目录 一、分割链表 二、奇偶链表 一、分割链表 给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。 你不需要 保留 每个分区中各节点的初始相对位置。 示例 1: 输…...
Python uiautomator2安卓自动化测试
一、前言 uiautomator2是Python对Android设备进行UI自动化的库,支持USB和WIFI链接,可以实现获取屏幕上任意一个APP的任意一个控件属性,并对其进行任意操作。 重点是它可以实现安卓自动化采集,甚至是群控采集,且安装和…...

Leetcode. 160相交链表
文章目录指针解法指针解法 核心思路 : 先 分别求两个链表的长度 然后长的链表先走 差距步(长-短) 最后长链表和短链表同时走 ,第一地址相同的就是交点 ,注意一定是地址相同 不可能出现上图这种情况 ,因为C1…...

MDPs —— 马尔可夫决策定义与算法
文章目录MDPs 定义——由实例开始时序决策问题给游戏增点乐子*为什么要有折扣游戏的解——原则所以,什么是 MDPs?MDPs 的基本原理、表示光环原理效用的求解是反向传播的原则不变条件MDPs 的表示MDPs 求解效用迭代法缺点原则迭代法MDPs 定义——由实例开始…...
【C++】图
本文包含了图的基本概念 1.相关概念 1.1 无/有向 无向图:每一个顶点之间的连线没有方向 有向图:连线有方向(类似离散数学的二元关系 <A,B>代表从A到B的边,有方向) <A,B>中A为始点,B为终点在…...

尾递归优化
文章目录1. 前言2. 什么尾调用(Tail Call)?3. 尾调用优化4. Linux内核下的尾递归优化使用5. 参考资料1. 前言 限于作者能力水平,本文可能存在谬误,对此给读者带来的损失,作者不错任何承诺。 2. 什么尾调用…...

P1120 小木棍(搜索+剪枝)
题目链接:P1120 小木棍 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 样例输入: 9 5 2 1 5 2 1 5 2 1 样例输出: 6 分析:这道题一看数据范围就知道是搜索,但关键是需要剪枝。 首先我们求出所有木棍的长度和&am…...
【专项训练】动态规划-3
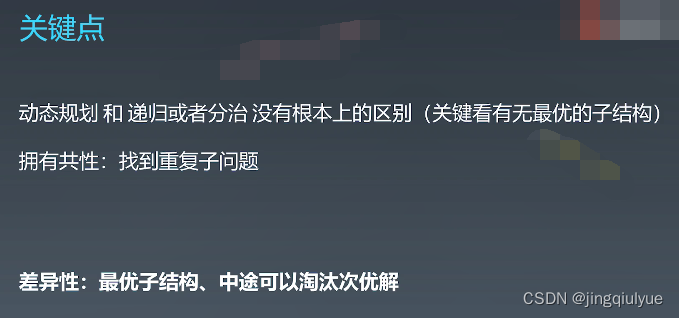
动态规划:状态转移方程、找重复性和最优子结构 分治 + 记忆化搜索,可以过度到动态规划(动态递推) function DP():# DP状态定义# 需要经验,需把现实问题定义为一个数组,一维、二维、三维……dp =[][] # 二维情况for i = 0...M:...
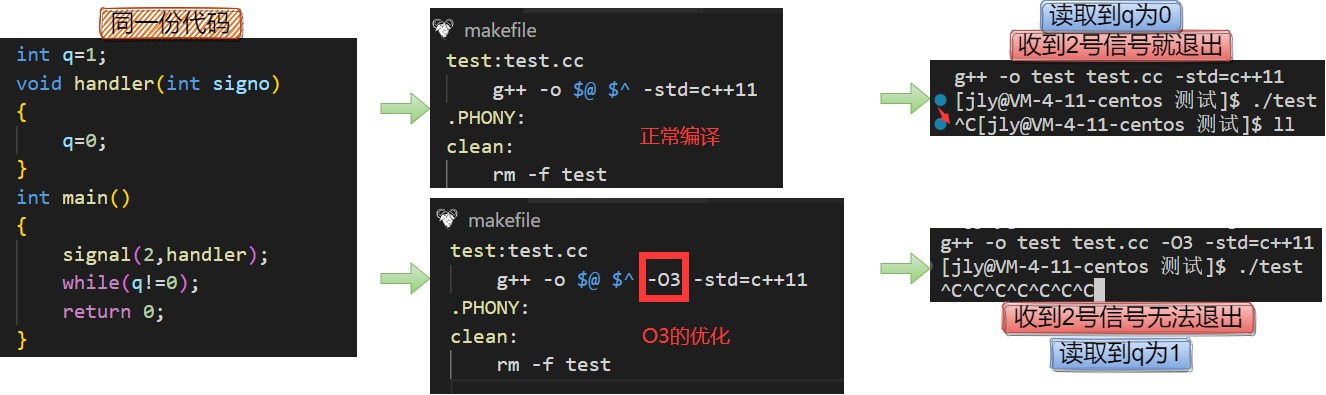
【Linux】信号+再谈进程地址空间
目录 一、Linux中的信号 1、Linux中的信号 2、进程对信号的处理 3、信号的释义 二、信号的捕捉 1、信号的捕捉signal() 2、信号的捕捉sigaction() 三、信号如何产生? 1、kill()用户调用kill向操作系统发送信号 通过命令行参数模仿写一个kill命令 2、rais…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...
