【算法刷题 | 动态规划14】6.28(最大子数组和、判断子序列、不同的子序列)

文章目录
- 35.最大子数组和
- 35.1题目
- 35.2解法:动规
- 35.2.1动规思路
- 35.2.2代码实现
- 36.判断子序列
- 36.1题目
- 36.2解法:动规
- 36.2.1动规思路
- 36.2.2代码实现
- 37.不同的子序列
- 37.1题目
- 37.2解法:动规
- 37.2.1动规思路
- 37.2.2代码实现
35.最大子数组和
35.1题目
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组
是数组中的一个连续部分。
- 示例一:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6
- 示例二:
输入:nums = [1]
输出:1
35.2解法:动规
35.2.1动规思路
-
确定dp数组以及下标含义:
dp[i]:下标为i的子数组的最大子数组和为dp[i]
-
确定递推公式:dp[i]=Math.max( dp[i-1]+nums[i],nums[i])
-
dp数组初始化:dp[0]=Math.max(0,nums[i])
-
确定遍历顺序:从前往后
-
举例推导:
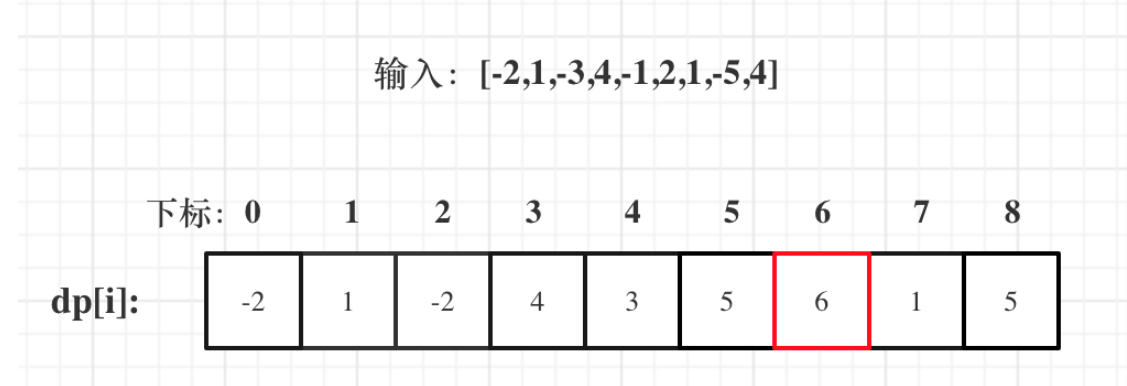
35.2.2代码实现
public int maxSubArray(int[] nums) {int[] dp=new int[nums.length];int result=nums[0];dp[0]=nums[0];for(int i=1;i<nums.length;i++){dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);result=Math.max(result,dp[i]);}return result;}
36.判断子序列
36.1题目
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
进阶:
如果有大量输入的 S,称作 S1, S2, … , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
- 示例一:
输入:s = "abc", t = "ahbgdc"
输出:true
- 示例二:
输入:s = "axc", t = "ahbgdc"
输出:false
36.2解法:动规
36.2.1动规思路
-
确定dp数组以及下标含义:
dp(i)(j):表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同的子序列的长度为dp(i)(j)
-
确定递推公式:
2.1 s[i-1]=t[j-1]:t中找到了一个字符,在s中也出现,即dp(i)(j)=dp(i-1)(j-1)+1
2.2 s[i-1]!=t[j-1]:t下标j-1位置的字符和s下标i-1位置的字符不同,即dp(i)(j)=dp(i)(j-1)
-
dp数组初始化:dp(i)(0)和dp(0)(j)位置的元素没有意义
-
确定遍历顺序:从上到下
-
举例推导:
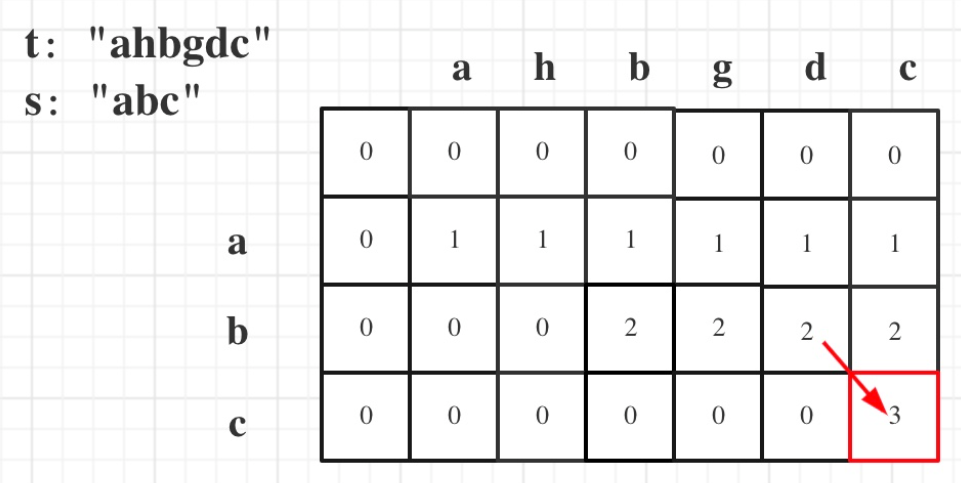
36.2.2代码实现
public boolean isSubsequence(String s, String t) {int[][] dp=new int[s.length()+1][t.length()+1];for(int i=1;i<=s.length();i++){for(int j=1;j<=t.length();j++){if(s.charAt(i-1)==t.charAt(j-1)){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=dp[i][j-1];}}}return dp[s.length()][t.length()]==s.length();}
37.不同的子序列
37.1题目
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 + 7 取模。
- 示例一:
输入:s = "rabbbit", t = "rabbit"
输出:3
解释:
如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit
rabbbit
rabbbit
- 示例二:
输入:s = "babgbag", t = "bag"
输出:5
解释:
如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。
babgbag
babgbag
babgbag
babgbag
babgbag
37.2解法:动规
37.2.1动规思路
-
求解:求子序列s组装成t的几种方法!!!
-
确定dp数组以及下标含义:
dp(i)(j):以下标i-1为结尾的s子序列中 出现 以下标j-1为结尾的t子序列的个数 为dp(i)(j)
-
确定递推公式:
3.1 s[i-1]=j[j-1]:两种情况,取s[i-1]或不取,即dp(i)(j)=dp(i-1)(j-1)+dp(i-1)(j)
3.2 s[i-1]!=[j-1]:只能不取s[i-1],即dp(i)(j)=dp(i-1)(j)
-
dp数组初始化:
dp(i)(0):子序列s组装成空串的方法肯定有一种
dp(0)(j):无意义
-
确定遍历顺序:从上到下
-
举例推导:
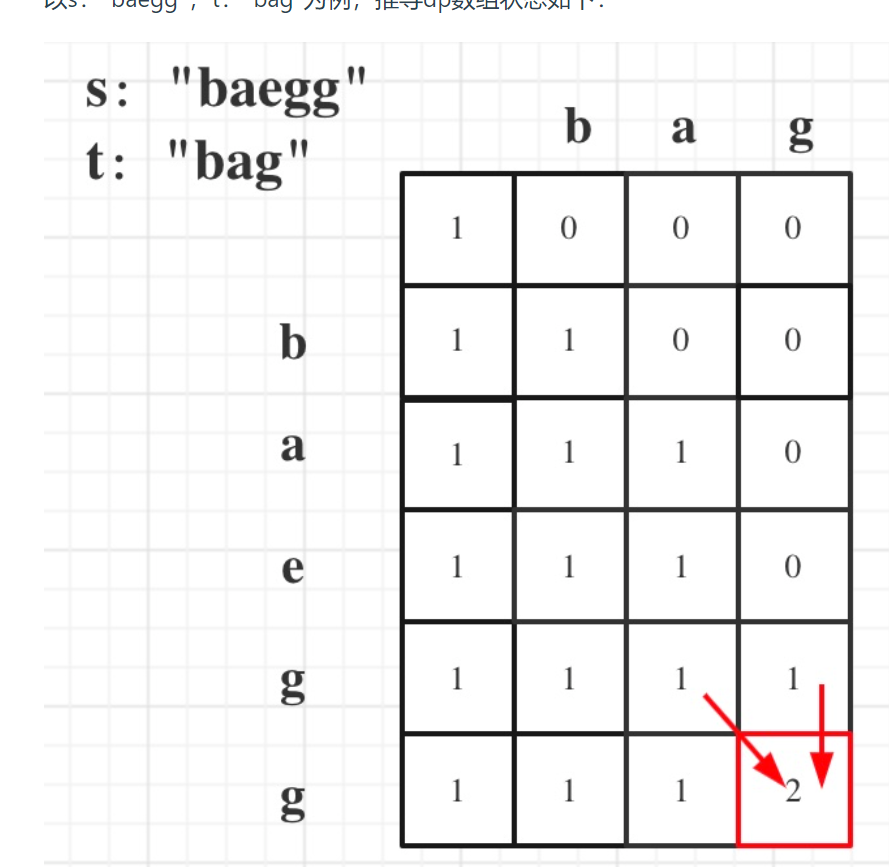
37.2.2代码实现
public int numDistinct(String s, String t) {int[][] dp=new int[s.length()+1][t.length()+1];//初始化for(int i=0;i<=s.length();i++){dp[i][0]=1;}for(int i=1;i<=s.length();i++){for(int j=1;j<=t.length();j++){if(s.charAt(i-1)==t.charAt(j-1)){//两种情况:取/不取dp[i][j]=dp[i-1][j-1]+dp[i-1][j];}else{dp[i][j]=dp[i-1][j];}}}return dp[s.length()][t.length()];}

相关文章:

【算法刷题 | 动态规划14】6.28(最大子数组和、判断子序列、不同的子序列)
文章目录 35.最大子数组和35.1题目35.2解法:动规35.2.1动规思路35.2.2代码实现 36.判断子序列36.1题目36.2解法:动规36.2.1动规思路36.2.2代码实现 37.不同的子序列37.1题目37.2解法:动规37.2.1动规思路37.2.2代码实现 35.最大子数组和 35.1…...
vue3 vxe-grid列中绑定vxe-switch实现数据更新
1、先上一张图: <template #valueSlot"{ row }"><vxe-switch :value"getV(row.svalue)" change"changeSwitch(row)" /></template>function getV(value){return value 1;};function changeSwitch(row) {console.l…...

Hive SQL:实现炸列(列转行)以及逆操作(行转列)
目录 列转行行转列 列转行 函数: EXPLODE(ARRAY):将ARRAY中的每一元素转换为每一行 EXPLODE(MAP):将MAP中的每个键值对转换为两行,其中一行数据包含键,另一行数据包含值 数据样例: 1、将每天的课程&#…...

MD5算法详解
哈希函数 是一种将任意输入长度转变为固定输出长度的函数。 一些常见哈希函数有:MD5、SHA1、SHA256。 MD5算法 MD5算法是一种消息摘要算法,用于消息认证。 数据存储方式:小段存储。 数据填充 首先对我们明文数据进行处理,使其…...

ES6的代理模式-Proxy
语法 target 要使用 Proxy 包装的目标对象(可以是任何类型的对象,包括原生数组,函数,甚至另一个代理handler 一个通常以函数作为属性的对象,用来定制拦截行为 const proxy new Proxy(target, handle)举个例子 <s…...

排序(堆排序、快速排序、归并排序)-->深度剖析(二)
前言 前面介绍了冒泡排序、选择排序、插入排序、希尔排序,作为排序中经常用到了算法,还有堆排序、快速排序、归并排序 堆排序(HeaSort) 堆排序的概念 堆排序是一种有效的排序算法,它利用了完全二叉树的特性。在C语言…...

七一建党节|热烈庆祝中国共产党成立103周年!
时光荏苒,岁月如梭。 在这热情似火的夏日, 我们迎来了中国共产党成立103周年的重要时刻。 这是一个值得全体中华儿女共同铭记和庆祝的日子, 也是激励我们不断前进的重要时刻。 103年, 风雨兼程,砥砺前行。 从嘉兴…...

Spring Boot应用知识梳理
一.简介 Spring Boot 是一个用于快速开发基于 Spring 框架的应用程序的工具。它简化了基于 Spring 的应用程序的配置和部署过程,提供了一种快速、便捷的方式来构建独立的、生产级别的 Spring 应用程序。 Spring Boot 的一些主要优点包括: 1. 简化配置…...

Spring中利用重载与静态分派
Spring中利用重载与静态分派 在Java和Spring框架中,重载(Overloading)和静态分派(Static Dispatch)是两个非常重要的概念,它们在处理类方法选择和执行过程中扮演着关键角色。本文旨在深入探讨Spring环境下…...

文本三剑客之awk:
文本三剑客awk: grep 查 sed 增删改查 主要:增改 awk 按行取列 awk awk默认的分隔符:空格,tab键,多个空格自动压缩为一个。 awk的工作原理:根据指令信息,逐行的读取文本内容,然…...

SpringSecurity-授权示例
用户基于权限进行授权 定义用户与权限 authorities()。 package com.cms.config;import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration; import org.springframework.security.core.userdetails.User; import…...

选哪个短剧系统源码好:全面评估与决策指南
在短剧内容创作和分享日益流行的今天,选择合适的短剧系统源码对于构建一个成功的短剧平台至关重要。短剧系统源码不仅关系到平台的稳定性和用户体验,还直接影响到内容创作者和观众的互动质量。本文将提供一份全面的评估指南,帮助您在众多短剧…...

AI时代的软件工程:挑战与改变
人工智能(AI)正以惊人的速度改变着我们的生活和工作方式。作为与AI关系最为密切的领域之一,软件工程正经历着深刻的转变。 1 软件工程的演变 软件工程的起源 软件工程(Software Engineering)是关于如何系统化、规范化地…...

Zuul介绍
Zuul 是 Netflix 开源的一个云平台网络层代理,它主要用于路由、负载均衡、中间件通信和动态路由。Zuul 本质上是一个基于 JVM 的网关,它提供了以下功能: 1.路由:Zuul 允许客户端和服务器之间的所有入站和出站请求通过一个中心化的…...
7-1作业
1.实验目的:完成字符收发 led.h #ifndef __GPIO_H__ #define __GPIO_H__#include "stm32mp1xx_rcc.h" #include "stm32mp1xx_gpio.h" #include "stm32mp1xx_uart.h"//RCC,GPIO,UART初始化 void init();//字符数据发送 void set_tt…...

ElasticSearch安装、配置详细步骤
一、环境及版本介绍 操作系统: Windows 10 软件版本: elasticsearch-7.17.22、kibana-7.17.22、IK-7.17.22 开发环境选择软件版本应提前考虑正式系统环境,否则会产生软件与服务器环境不兼容的问题出现,ElasticSearch与环境支持…...
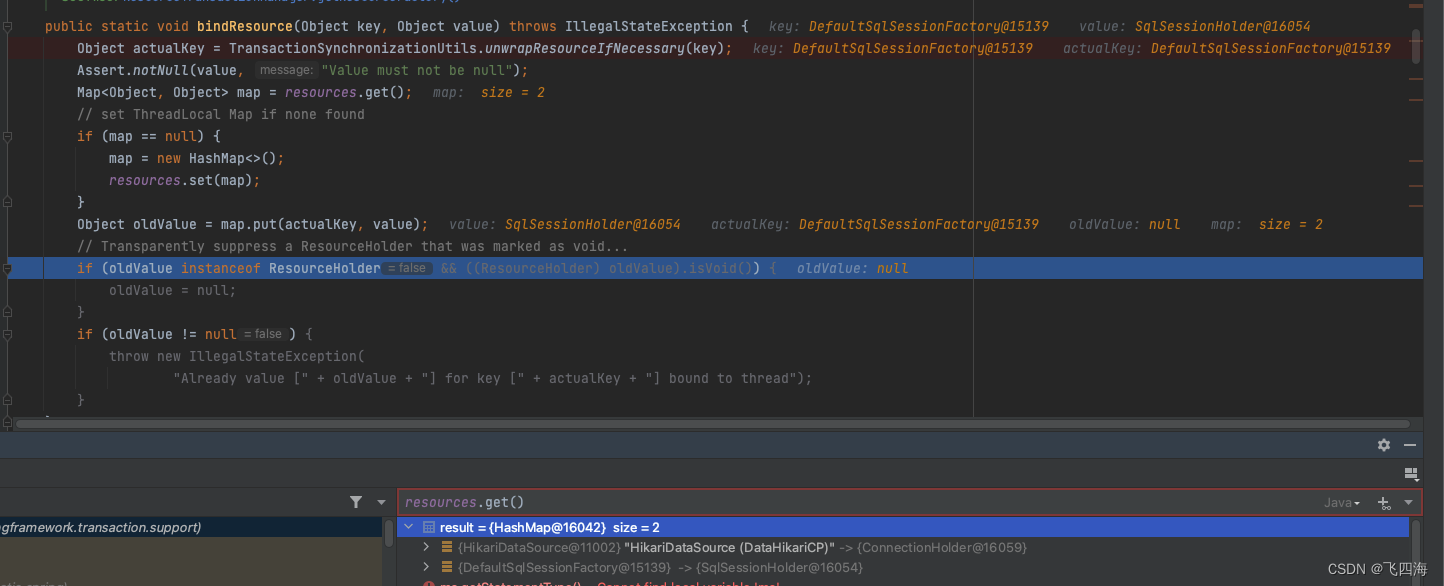
【Mybatis 与 Spring】事务相关汇总
之前分享的几篇文章可以一起看,形成一个体系 【Mybatis】一级缓存与二级缓存源码分析与自定义二级缓存 【Spring】Spring事务相关源码分析 【Mybatis】Mybatis数据源与事务源码分析 Spring与Mybaitis融合 SpringManagedTransaction: org.mybatis.spri…...
)
Leetcode 2065. 最大化一张图中的路径价值(DFS / 最短路)
Leetcode 2065. 最大化一张图中的路径价值 暴力DFS 容易想到,从0点出发DFS,期间维护已经走过的距离(时间)和途径点的权值之和,若访问到0点则更新答案,若下一步的距离与已走过的距离和超出了maxTime&#…...
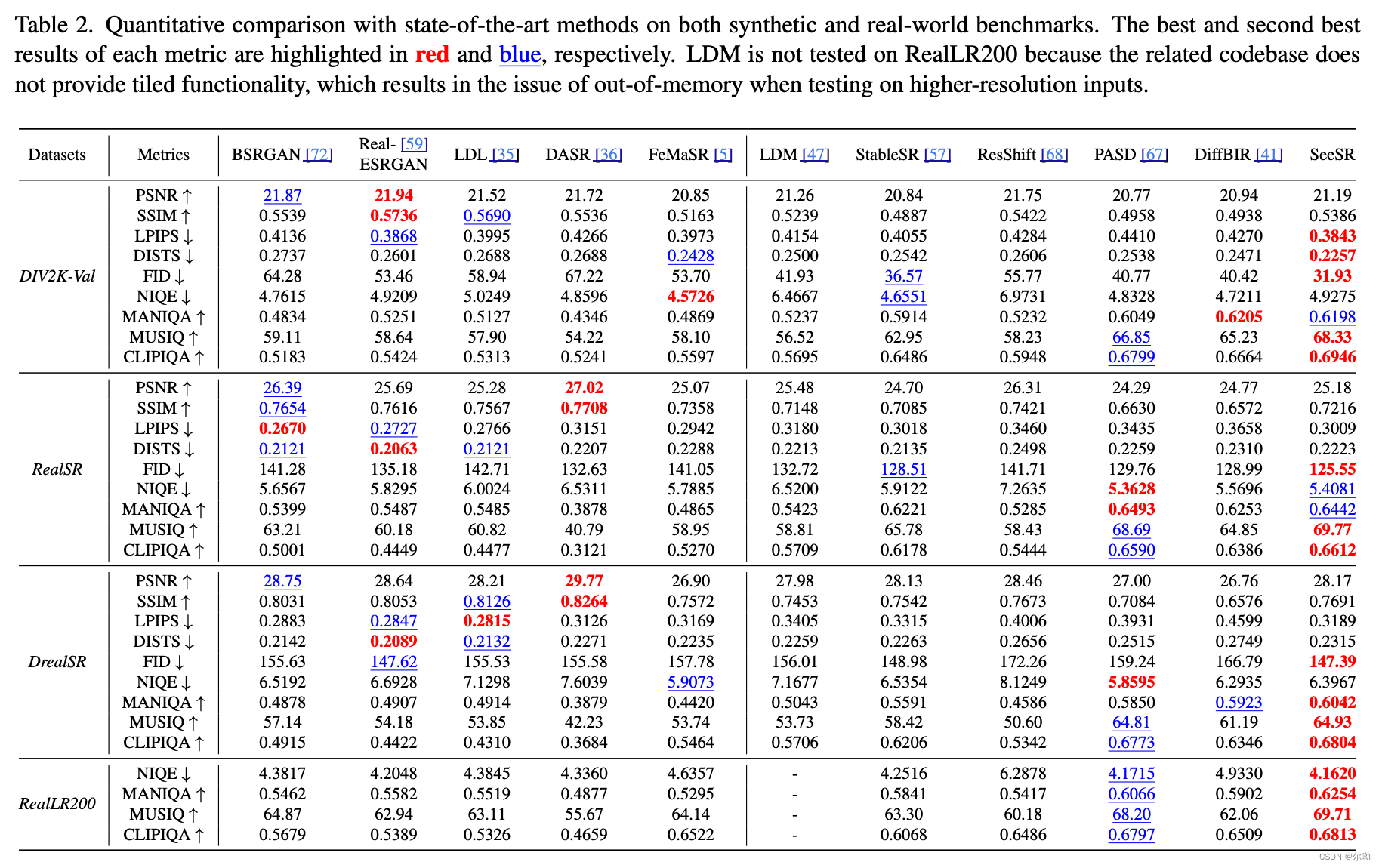
SeeSR: Towards Semantics-Aware Real-World Image Super-Resolution
CVPR2024 香港理工大学&OPPO&bytedancehttps://github.com/cswry/SeeSR?tabreadme-ov-file#-licensehttps://arxiv.org/pdf/2311.16518#page5.80 问题引入 因为有些LR退化情况比较严重,所以超分之后的结果会出现语义的不一致的情况,所以本文训…...
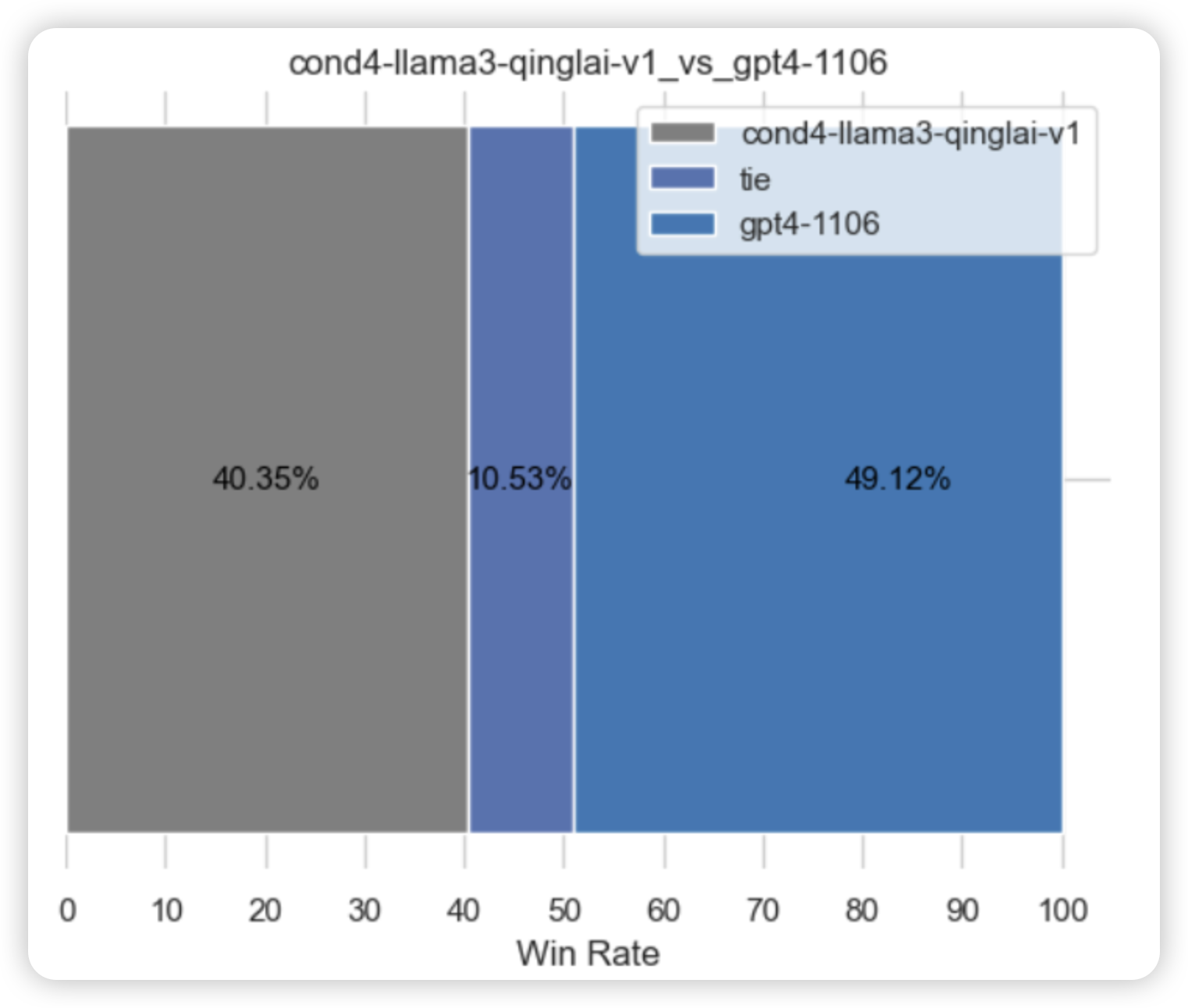
七月论文审稿GPT第5版:拿我司七月的早期paper-7方面review数据集微调LLama 3
前言 llama 3出来后,为了通过paper-review的数据集微调3,有以下各种方式 不用任何框架 工具 技术,直接微调原生的llama 3,毕竟也有8k长度了 效果不期望有多高,纯作为baseline通过PI,把llama 3的8K长度扩展…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
