【Matlab 六自由度机器人】机器人动力学之推导拉格朗日方程(附MATLAB机器人动力学拉格朗日方程推导代码)
【Matlab 六自由度机器人】机器人动力学概述
- 近期更新
- 前言
- 正文
- 一、拉格朗日方程的推导
- 1. 单自由度系统
- 2. 单连杆机械臂系统
- 3. 双连杆机械臂系统
- 二、MATLAB实例推导
- 1. 机器人模型的建立
- 2. 动力学代码
- 总结
- 参考文献
近期更新
【汇总】
【Matlab 六自由度机器人】系列文章汇总 \fcolorbox{green}{aqua}{【Matlab 六自由度机器人】系列文章汇总 } 【Matlab 六自由度机器人】系列文章汇总
【主线】
运动学 \color{red}运动学 运动学
- 定义标准型及改进型D-H参数,建立机器人模型。
- 运动学正解
- 基于蒙特卡罗方法(Monte Carlo Method)构建机器人工作空间
动力学 \color{red}动力学 动力学
(待补充)
【补充说明】
- 关于灵活工作空间与可达工作空间的理解
- 关于改进型D-H参数(modified Denavit-Hartenberg)的详细建立步骤
- 关于旋转的参数化(欧拉角、姿态角、四元数)的相关问题
- 关于双变量函数atan2(x,y)的解释
- 关于机器人运动学反解的有关问题
前言
本篇对机器人动力学进行一个概述。
之前谈到的运动学方程仅描述了机器人的运动过程,没有考虑到产生运动的力和扭矩,而动力学方程能描述力和运动之间的关系,因此我们在此引入动力学的概念。
本人在读研期间仅在机器人运动学的基础上完成论文的撰写,有些遗憾未能将机器人动力学应用到文章之中,在此写下机器人动力学的概述以及学习过程中遇到的问题和解决思路。
以下是本篇文章正文内容
分析机器人操作的动态数学模型,主要采用下列两种理论
- 动力学基本理论,包括牛顿欧拉方程。
- 拉格朗日力学,特别是二阶拉格朗日方程。
第一个方法:牛顿—欧拉方程即力的动态平衡法。当用此法时,需从运动学出发求得加速度,并消去各内作用力。对于较复杂的系统,此种分析方法十分复杂与麻烦。
第二个方法:拉格朗日方程即拉格朗日功能平衡法,也称为欧拉—拉格朗日方程,它只需要速度而不必求内作用力。因此,这是一种直截了当和简便的方法。
在本篇文章中主要采用拉格朗日方程来分析和求解机械手的动力学问题。
正文
一、拉格朗日方程的推导
1. 单自由度系统
我们以图中所示的单自由度系统为例,来说明如何从牛顿第二定律推导出拉格朗日方程。图中的圆点为带有质量的一个粒子,下面称为质点。该质点受到重力 g g g的效果和拉力 f f f的效果。

质量为 m m m的粒子受到限制,只能在垂直方向移动,这就构成了一个单自由度系统。 重力 m g mg mg向下作用, 外力 f f f则向上作用。
根据牛顿第二定律,这个系统中的质点的运动方程为:
m a = f − m g ⟹ m y ¨ = f − m g ma=f-mg\implies m\ddot{y}_{}^{}=f-mg ma=f−mg⟹my¨=f−mg
左侧的 m y ¨ m\ddot{y}_{}^{} my¨也可以用以下方程推出
m y ¨ = d d t ( m y ˙ ) = d d t ∂ ∂ y ˙ ( 1 2 m y ˙ 2 ) = d d t ( ∂ K ∂ y ˙ ) m\ddot{y}_{}^{}= \frac{\mathrm{d}}{\mathrm{d} t} \left(m\dot{y}\right) = \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial {}}{\partial \dot{y}} \left(\frac{1}{2}m\dot{y}^2\right)= \frac{\mathrm{d}}{\mathrm{d} t} \left(\frac{\partial \mathcal{K}}{\partial \dot{y}}\right) my¨=dtd(my˙)=dtd∂y˙∂(21my˙2)=dtd(∂y˙∂K)
注: m y ˙ 可以写作 ∂ ∂ y ˙ ( 1 2 m y ˙ 2 ) m\dot{y}可以写作\frac{\partial {}}{\partial \dot{y}} \left(\frac{1}{2}m\dot{y}^2\right) my˙可以写作∂y˙∂(21my˙2),即 1 2 m y ˙ 2 \frac{1}{2}m\dot{y}^2 21my˙2对 y y y进行求偏导。
其中,动能 K = 1 2 m y ˙ 2 \mathcal{K}= \frac{1}{2} m\dot{y}^2 K=21my˙2
类似上面的方程,我们可以将重力表达为:
m g = ∂ ∂ y ( m g y ) = ∂ P ∂ y mg=\frac{\partial }{\partial {y}}\left(mgy\right)= \frac{\partial \mathcal{P}}{\partial {y}} mg=∂y∂(mgy)=∂y∂P
其中,重力势能 P = m g y \mathcal{P}= mgy P=mgy
定义函数 L \mathcal{L} L,它是系统的动能和势能之差,也称为系统的拉格朗日算子
L = K − P = 1 2 m y ˙ 2 − m g y \mathcal{L}= \mathcal{K}- \mathcal{P}=\frac{1}{2}m\dot{y}^2-mgy L=K−P=21my˙2−mgy
① L 对 y ˙ 求偏导,可得到 ∂ L ∂ y ˙ = ∂ K ∂ y ˙ ① \mathcal{L}对\dot{y}求偏导,可得到\frac{\partial { \mathcal{L}}}{\partial \dot{y}}=\frac{\partial { \mathcal{K}}}{\partial \dot{y}} ①L对y˙求偏导,可得到∂y˙∂L=∂y˙∂K
② L 对 y ˙ 求偏导,可得到 ∂ L ∂ y = − ∂ P ∂ y ⟹ ∂ P ∂ y = − ∂ L ∂ y ② \mathcal{L}对\dot{y}求偏导,可得到\frac{\partial { \mathcal{L}}}{\partial {y}}=-\frac{\partial { \mathcal{P}}}{\partial {y}} \implies \frac{\partial { \mathcal{P}}}{\partial {y}}=-\frac{\partial { \mathcal{L}}}{\partial {y}} ②L对y˙求偏导,可得到∂y∂L=−∂y∂P⟹∂y∂P=−∂y∂L
那么对上式的 m y ¨ = f − m g m\ddot{y}_{}^{}=f-mg my¨=f−mg可以写作如下公式
d d t ∂ L ∂ y ˙ = f − ( − ∂ L ∂ y ) ⟹ f = d d t ∂ L ∂ y ˙ − ∂ L ∂ y \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial { \mathcal{L}}}{\partial \dot{y}}=f- \left(-\frac{\partial \mathcal{L}}{\partial {y}}\right) \implies f=\frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial { \mathcal{L}}}{\partial \dot{y}}-\frac{\partial \mathcal{L}}{\partial {y}} dtd∂y˙∂L=f−(−∂y∂L)⟹f=dtd∂y˙∂L−∂y∂L
至此,单自由度系统的拉格朗日方程就推导出来了,方程如下:
f = d d t ∂ L ∂ y ˙ − ∂ L ∂ y f=\frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial { \mathcal{L}}}{\partial \dot{y}}-\frac{\partial \mathcal{L}}{\partial {y}} f=dtd∂y˙∂L−∂y∂L
下面是建立拉格朗日函数的一般步骤
首先写出系统的动能和势能,并以广义坐标 ( q 1 , ⋯ , q n ) \left(q_{1}, \cdots, q_{n}\right) (q1,⋯,qn) 的形式来表示,其中 n n n 是系统的自由度数目;然后,根据下述公式来计算 n − n^{-} n−自由度系统的运动方程
d d t ∂ L ∂ q ˙ k − ∂ L ∂ q k = τ k , k = 1 , ⋯ , n \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial \mathcal{L}}{\partial \dot{q}_{k}}-\frac{\partial \mathcal{L}}{\partial q_{k}}=\tau_{k}, \quad k=1, \cdots, n dtd∂q˙k∂L−∂qk∂L=τk,k=1,⋯,n
其中, τ k \tau_{k} τk 是与广义坐标 q k q_{k} qk 相关的广义力。
在上述单自由度系统的例子中,变量 y y y 作为广义坐标。欧拉-拉格朗日方程不仅可以导出一组耦合的二阶常微分方程,它还提供了一种 等同于通过牛顿第二定律得到动力学方程的构造方法。然而,正如我们将要看到的那样,对于诸如多连杆机器人等复杂系统,使用拉格朗日方法更为有利。
下面介绍单连杆机械臂系统和双连杆机械臂系统的拉格朗日方程
2. 单连杆机械臂系统
如下图中所示的单连杆机器人,它包括一个刚性连杆,该连杆通过齿轮系连接到直流电机。令 θ l \theta_l θl和 θ m \theta_m θm分别表示连杆和电机轴的转动角度。那么 θ m = r θ l \theta_m=r\theta_l θm=rθl,其中 r : 1 r: 1 r:1为齿轮变速比。如果连杆一端直接接在电机的旋转轴上,那么 r = 1 r=1 r=1。连杆转角和电机轴转角之间的代数关系表明该系统只有一个自由度,因此我们可以将 θ l \theta_l θl或 θ m \theta_m θm作为广义坐标。

单连杆机器人:电机输出轴通过齿轮系耦连到连杆的转动轴,齿轮系放大了电机扭矩并降低了电机转速。
在此选用 θ ℓ \theta_\ell θℓ作为广义坐标
系统的动能可以表示为 θ ℓ \theta_\ell θℓ的函数,其表示如下所示
K = 1 2 J m θ ˙ m 2 + 1 2 J ℓ θ ˙ ℓ 2 = 1 2 J m r 2 θ ˙ ℓ 2 + 1 2 J ℓ θ ˙ ℓ 2 = 1 2 ( r 2 J m + J ℓ ) θ ˙ ℓ 2 \mathcal{K} =\frac{1}{2}J_{m} \dot{\theta}_{m}^{2}+\frac{1}{2} J_{\ell} \dot{\theta}_{\ell}^{2} =\frac{1}{2}J_{m}r^2 \dot{\theta}_{\ell}^{2}+\frac{1}{2} J_{\ell} \dot{\theta}_{\ell}^{2} =\frac{1}{2}\left(r^{2} J_{m}+J_{\ell}\right) \dot{\theta}_{\ell}^{2} K=21Jmθ˙m2+21Jℓθ˙ℓ2=21Jmr2θ˙ℓ2+21Jℓθ˙ℓ2=21(r2Jm+Jℓ)θ˙ℓ2
其中, J m , J ℓ J_m,J_\ell Jm,Jℓ分别为电机和连杆的转动惯量。系统的势能如下所示
P = M g ℓ ( 1 − cos θ ℓ ) \mathcal{P}=Mg\ell\left(1-\cos \theta_{\ell}\right) P=Mgℓ(1−cosθℓ)
其中, M M M 是连杆的总体质量, ℓ \ell ℓ 是关节轴线与连杆质心之间的距离。定义 J = r 2 J m + J ℓ J=r^{2} J_{m}+J_{\ell} J=r2Jm+Jℓ,拉格朗日算子 L \mathcal{L} L如下
L = 1 2 J θ ˙ ℓ 2 − M g ℓ ( 1 − cos θ ℓ ) \mathcal{L}=\frac{1}{2} J \dot{\theta}_{\ell}^{2}-M g \ell\left(1-\cos \theta_{\ell}\right) L=21Jθ˙ℓ2−Mgℓ(1−cosθℓ)
将上述表达式代人到公式 d d t ∂ L ∂ q ˙ k − ∂ L ∂ q k = τ k , \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial \mathcal{L}}{\partial \dot{q}_{k}}-\frac{\partial \mathcal{L}}{\partial q_{k}}=\tau_{k}, dtd∂q˙k∂L−∂qk∂L=τk,中,其中 n = 1 n=1 n=1,广义坐标为 θ ℓ \theta_{\ell} θℓ,得到下列运动方程
J θ ¨ ℓ + M g ℓ sin θ ℓ = τ ℓ J \ddot{\theta}{ }_{\ell}+M g \ell \sin \theta_{\ell}=\tau_{\ell} Jθ¨ℓ+Mgℓsinθℓ=τℓ
广义力 τ ℓ \tau_{\ell} τℓ 表示那些无法从势函数推导出的外力和外力矩。对于这个例子, τ ℓ \tau_{\ell} τℓ 包括反映 到连杆上的电机输入力矩 u = r τ m u=r \tau_{m} u=rτm,以及 (非保守) 阻尼力矩 B m θ ˙ m B_{m} \dot{\theta}_{m} Bmθ˙m 和 B ℓ θ ˙ 1 B_{\ell} \dot{\theta}_{1} Bℓθ˙1 。将电机阻尼反映到连杆上,得出
τ ℓ = u − B θ ˙ ℓ ⟹ u = τ ℓ + B θ ˙ ℓ \tau_{\ell}=u-B \dot{\theta}_{\ell} \implies u=\tau_{\ell}+B \dot{\theta}_{\ell} τℓ=u−Bθ˙ℓ⟹u=τℓ+Bθ˙ℓ
其中, B = r B m + B ℓ B=r B_{m}+B_{\ell} B=rBm+Bℓ 。因此,该系统完整的动力学表达式为
u = J θ ¨ ℓ + B θ ˙ ℓ + M g ℓ sin θ ℓ u=J \ddot{\theta}_{\ell}+B \dot{\theta}_{\ell}+M g \ell \sin \theta_{\ell} u=Jθ¨ℓ+Bθ˙ℓ+Mgℓsinθℓ
3. 双连杆机械臂系统
下面推导双连杆机械臂系统的动能和位能,如下图。这种运动机构具有开式运动链,与复摆运动有许多相似之处。

图中
T 1 T_{1} T1 和 T 2 T_{2} T2 为转矩;m 1 m_{1} m1 和 m 2 m_{2} m2为连杆1和连杆2的质量,该连杆的质量以连杆末端的质点来进行表示;
d 1 d_{1} d1 和 d 2 d_{2} d2分别为两连杆的长度;
θ 1 \theta_{1} θ1 和 θ 2 \theta_{2} θ2为广义坐标;
g g g为重力加速度。
先计算连杆1的动能 K 1 {K_1} K1和动能 P 1 {P_1} P1
K 1 = 1 2 m 1 v 1 2 v 1 = d 1 θ ˙ 1 P 1 = m 1 g h h 1 = − d 1 cos θ 1 \begin{aligned} {K_1}&=\frac{1}{2} m_{1} v_{1}^{2} \\ v_{1}&=d_{1} \dot{\theta}_{1} \\ {P_1}&=m_1gh \\ h_1&=-d_{1} \cos \theta_{1} \end{aligned} K1v1P1h1=21m1v12=d1θ˙1=m1gh=−d1cosθ1
推导得
K 1 = 1 2 m 1 d 1 2 θ ˙ 1 2 P 1 = − m 1 g d 1 cos θ 1 \begin{aligned} K_{1}&=\frac{1}{2} m_{1} d_{1}^{2} \dot{\theta}_{1}^{2} \\ P_{1}&=-m_{1} g d_{1} \cos \theta_{1} \end{aligned} K1P1=21m1d12θ˙12=−m1gd1cosθ1
再求连杆 2 的动能 K 2 K_{2} K2 和位能 P 2 P_{2} P2 。
K 2 = 1 2 m 2 v 2 2 P 2 = m g y 2 \begin{aligned} K_{2}&=\frac{1}{2} m_{2} v_{2}^{2}\\ P_{2}&=m g y_{2} \end{aligned} K2P2=21m2v22=mgy2式中
v 2 2 = x ˙ 2 2 + y ˙ 2 2 x 2 = d 1 sin θ 1 + d 2 sin ( θ 1 + θ 2 ) y 2 = − d 1 cos θ 1 − d 2 cos ( θ 1 + θ 2 ) x ˙ 2 = d 1 cos θ 1 θ ˙ 1 + d 2 cos ( θ 1 + θ 2 ) ( θ ˙ 1 + θ ˙ 2 ) y ˙ 2 = d 1 sin θ 1 θ ˙ 1 + d 2 sin ( θ 1 + θ 2 ) ( θ ˙ 1 + θ ˙ 2 ) \begin{aligned} v_{2}^{2}&=\dot{x}_{2}^{2}+\dot{y}_{2}^{2} \\ x_{2}&=d_{1} \sin \theta_{1}+d_{2} \sin \left(\theta_{1}+\theta_{2}\right) \\ y_{2}&=-d_{1} \cos \theta_{1}-d_{2} \cos \left(\theta_{1}+\theta_{2}\right) \\ \dot{x}_{2}&=d_{1} \cos \theta_{1} \dot{\theta}_{1}+d_{2} \cos \left(\theta_{1}+\theta_{2}\right)\left(\dot{\theta}_{1}+\dot{\theta}_{2}\right) \\ \dot{y}_{2}&=d_{1} \sin \theta_{1} \dot{\theta}_{1}+d_{2} \sin \left(\theta_{1}+\theta_{2}\right)\left(\dot{\theta}_{1}+\dot{\theta}_{2}\right) \end{aligned} v22x2y2x˙2y˙2=x˙22+y˙22=d1sinθ1+d2sin(θ1+θ2)=−d1cosθ1−d2cos(θ1+θ2)=d1cosθ1θ˙1+d2cos(θ1+θ2)(θ˙1+θ˙2)=d1sinθ1θ˙1+d2sin(θ1+θ2)(θ˙1+θ˙2)
于是可求得
v 2 2 = d 1 2 θ ˙ 1 2 + d 2 2 ( θ ˙ 1 2 + 2 θ ˙ 1 θ ˙ 2 + θ ˙ 2 2 ) + 2 d 1 d 2 cos θ 2 ( θ ˙ 1 2 + θ ˙ 1 θ ˙ 2 ) \boldsymbol{v}_{2}^{2}=d_{1}^{2} \dot{\theta}_{1}^{2}+d_{2}^{2}\left(\dot{\theta}_{1}^{2}+2 \dot{\theta}_{1} \dot{\theta}_{2}+\dot{\theta}_{2}^{2}\right)+2 d_{1} d_{2} \cos \theta_{2}\left(\dot{\theta}_{1}^{2}+\dot{\theta}_{1} \dot{\theta}_{2}\right) v22=d12θ˙12+d22(θ˙12+2θ˙1θ˙2+θ˙22)+2d1d2cosθ2(θ˙12+θ˙1θ˙2)
以及
K 2 = 1 2 m 2 d 1 2 θ ˙ 1 2 + 1 2 m 2 d 2 2 ( θ ˙ 1 + θ ˙ 2 ) 2 + m 2 d 1 d 2 cos θ 2 ( θ ˙ 1 2 + θ ˙ 1 θ ˙ 2 ) P 2 = − m 2 g d 1 cos θ 1 − m 2 g d 2 cos ( θ 1 + θ 2 ) \begin{gathered} K_{2}&=\frac{1}{2} m_{2} d_{1}^{2} \dot{\theta}_{1}^{2}+\frac{1}{2} m_{2} d_{2}^{2}\left(\dot{\theta}_{1}+\dot{\theta}_{2}\right)^{2}+m_{2} d_{1} d_{2} \cos \theta_{2}\left(\dot{\theta}_{1}^{2}+\dot{\theta}_{1} \dot{\theta}_{2}\right) \\ P_{2}&=-m_{2} g d_{1} \cos \theta_{1}-m_{2} g d_{2} \cos \left(\theta_{1}+\theta_{2}\right) \end{gathered} K2P2=21m2d12θ˙12+21m2d22(θ˙1+θ˙2)2+m2d1d2cosθ2(θ˙12+θ˙1θ˙2)=−m2gd1cosθ1−m2gd2cos(θ1+θ2)
这样, 二连杆机械手系统的总动能和总位能分别为
K = K 1 + K 2 = 1 2 ( m 1 + m 2 ) d 1 2 θ ˙ 1 2 + 1 2 m 2 d 2 2 ( θ ˙ 1 + θ ˙ 2 ) 2 + m 2 d 1 d 2 cos θ 2 ( θ ˙ 1 2 + θ ˙ 1 θ ˙ 2 ) P = P 1 + P 2 = − ( m 1 + m 2 ) g d 1 cos θ 1 − m 2 g d 2 cos ( θ 1 + θ 2 ) \begin{aligned} K &=K_{1}+K_{2} \\ &=\frac{1}{2}\left(m_{1}+m_{2}\right) d_{1}^{2} \dot{\theta}_{1}^{2}+\frac{1}{2} m_{2} d_{2}^{2}\left(\dot{\theta}_{1}+\dot{\theta}_{2}\right)^{2}+m_{2} d_{1} d_{2} \cos \theta_{2}\left(\dot{\theta}_{1}^{2}+\dot{\theta}_{1} \dot{\theta}_{2}\right) \\ P &=P_{1}+P_{2} \\ &=-\left(m_{1}+m_{2}\right) g d_{1} \cos \theta_{1}-m_{2} g d_{2} \cos \left(\theta_{1}+\theta_{2}\right) \end{aligned} KP=K1+K2=21(m1+m2)d12θ˙12+21m2d22(θ˙1+θ˙2)2+m2d1d2cosθ2(θ˙12+θ˙1θ˙2)=P1+P2=−(m1+m2)gd1cosθ1−m2gd2cos(θ1+θ2)
二、MATLAB实例推导
1. 机器人模型的建立
- 根据文章上述的双连杆机械臂对其进行建模,具体建模方法可参阅以下文章:
- 定义标准型及改进型D-H参数建立机器人模型(附MATLAB建模代码)
- 【Matlab 六自由度机器人】关于改进型D-H参数(modified Denavit-Hartenberg)的详细建立步骤
单杆机械臂系统代码如下:
%% 单杆机械臂系统
clc
clear
close all
warning off%% MOD-DH参数
d1 = 0;
d2 = 100;
a1 = 0;
a2 = 0;
alpha1 = pi/2;
alpha2 = 0;
% theta d a alpha offset(关节变量偏移量)
L(1)=Link([0 d1 a1 alpha1 0 ],'modified');
L(2)=Link([0 d2 a2 alpha2 0 ],'modified');
Single_Robot = SerialLink(L,'name','SingleRobot');
Single_Robot.teach()
%限制机器人的关节空间
theta1min = -180; theta1max = 180;
theta2min = -180; theta2max = 180;
L(1).qlim = [theta1min theta1max]*pi/180;
L(2).qlim = [theta2min theta2max]*pi/180;
双连杆机械臂系统代码如下:
%% 双连杆机械臂系统
clc
clear
close all
warning off%% MOD-DH参数
d1 = 0;
d2 = 0;
d3 = 0;
a1 = 0;
a2 = 100;
a3 = 100;
alpha1 = pi/2;
alpha2 = 0;
alpha3 = 0;
% theta d a alpha offset(关节变量偏移量)
L(1)=Link([0 d1 a1 alpha1 0 ],'modified');
L(1).offset = -pi/2;
L(2)=Link([0 d2 a2 alpha2 0 ],'modified');
L(3)=Link([0 d3 a3 alpha3 0 ],'modified');
Double_Robot = SerialLink(L,'name','SingleRobot');
Double_Robot.display()
Double_Robot.teach()
%限制机器人的关节空间
theta1min = -180; theta1max = 180;
theta2min = -180; theta2max = 180;
theta3min = -180; theta3max = 180;
L(1).qlim = [theta1min theta1max]*pi/180;
L(2).qlim = [theta2min theta2max]*pi/180;
L(3).qlim = [theta3min theta3max]*pi/180;
接下来对其进行运动学上的轨迹规划:
- 对于单杆系统,其轨迹规划如下:
n = 1:100;
q0 = [0 0];
q1 = [30 30];% 由q0移动到q1
[q,qd,qdd] = jtraj(q0,q1,n);figure(2)
subplot(3,1,1)
plot(n,q)
subplot(3,1,2)
plot(n,qd)
subplot(3,1,3)
plot(n,qdd)
其效果如下图:

- 对于双连杆系统
n = 1:100;
q0 = [0 0 0];
q1 = [30 60 90];[q,qd,qdd] = jtraj(q0,q1,n);figure(2)
subplot(3,1,1)
plot(n,q)
subplot(3,1,2)
plot(n,qd)
subplot(3,1,3)
plot(n,qdd)
其效果如下图:

往后会对关节空间轨迹规划 j t r a j ( ) 函数 jtraj()函数 jtraj()函数 和 笛卡尔空间轨迹规划 c t r a j ( ) 函数 ctraj()函数 ctraj()函数 进行单独篇章的撰写和探讨。
至此,运动学的前期准备已经完毕,下面进行机器人动力学 拉格朗日方程的推导。
2. 动力学代码
使用robot.dyn()函数查看建立的机器人的动力学参数
代码如下:
% 查看robot机器人所有的连杆的动力学参数
robot.dyn;
% 查看robot机器人第n根连杆的动力学参数
robot.dyn(n);% 对Single_Robot进行动力学参数的设置总结
本篇对机器人动力学进行一个概述。
之前谈到的运动学方程仅描述了机器人的运动过程,没有考虑到产生运动的力和扭矩,而动力学方程能描述力和运动之间的关系,因此我们在此引入动力学的概念。
第一章是机器人动力学之推导拉格朗日方程的内容,本文详细介绍了如何理解拉格朗日方程以及如何进行推导,介绍了如何求出机构的动能及位能。
第二章是拉格朗日方程代码的实现。
参考文献
- 机器人学、机器视觉与控制:MATLAB算法基础
- 机器人学
- 机器人建模和控制
- MATLAB机器人工具箱(四)动力学
- MATLAB机器人工具箱【3】—— 动力学相关函数及用法
相关文章:

【Matlab 六自由度机器人】机器人动力学之推导拉格朗日方程(附MATLAB机器人动力学拉格朗日方程推导代码)
【Matlab 六自由度机器人】机器人动力学概述 近期更新前言正文一、拉格朗日方程的推导1. 单自由度系统2. 单连杆机械臂系统3. 双连杆机械臂系统 二、MATLAB实例推导1. 机器人模型的建立2. 动力学代码 总结参考文献 近期更新 【汇总】 【Matlab 六自由度机器人】系列文章汇总 …...
线下生鲜蔬果店做小程序有什么方法
生鲜蔬果是生活所需,大小商家众多,零售批发各种经营模式,小摊贩或是超市门店都有着目标客户或准属性群体。竞争和获客转化也促进着商家寻找客源和加快线上进程。 尤其是以微信社交为主的私域场景,普客/会员都需要精细化管理营收和…...

几种linux开机自启脚本的方法
几种linux开机自启脚本的方法 1. 脚本添加到init.d目录中2. 创建服务service(推荐)3. /etc/profile & /etc/profile.d(不推荐)4. /etc/rc.local 本文以启动jenkins节点为例,需要持久连接,实现开机自启 …...
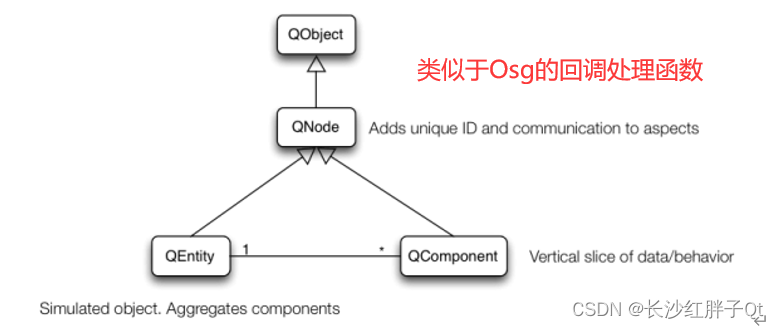
Qt开发笔记:Qt3D三维开发笔记(一):Qt3D三维开发基础概念介绍
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://blog.csdn.net/qq21497936/article/details/140059315 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、O…...
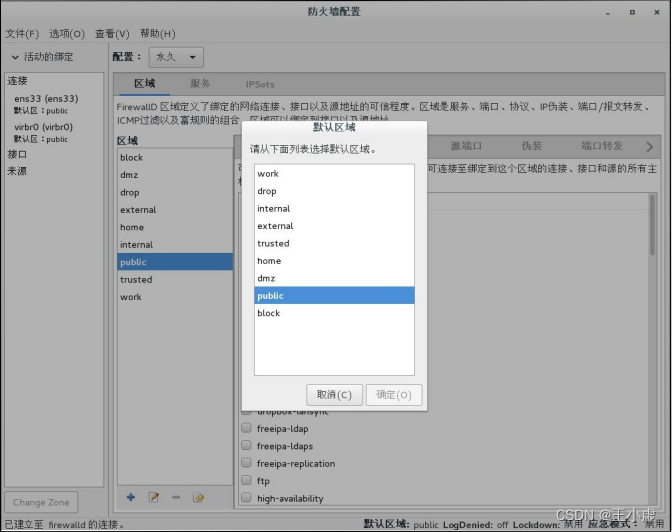
Firewalld 防火墙基础
Firewalld 防火墙基础 一、Firewalld概述firewalld 简介firewalld 和 iptables 的关系firewalld 与 iptables service 的区别 二、Firewalld 网络区域区域介绍Firewalld数据处理流程 三、Firewalld 防火墙的配置方法firewall-config 图形工具“区域”选项卡“服务”选项卡改变防…...
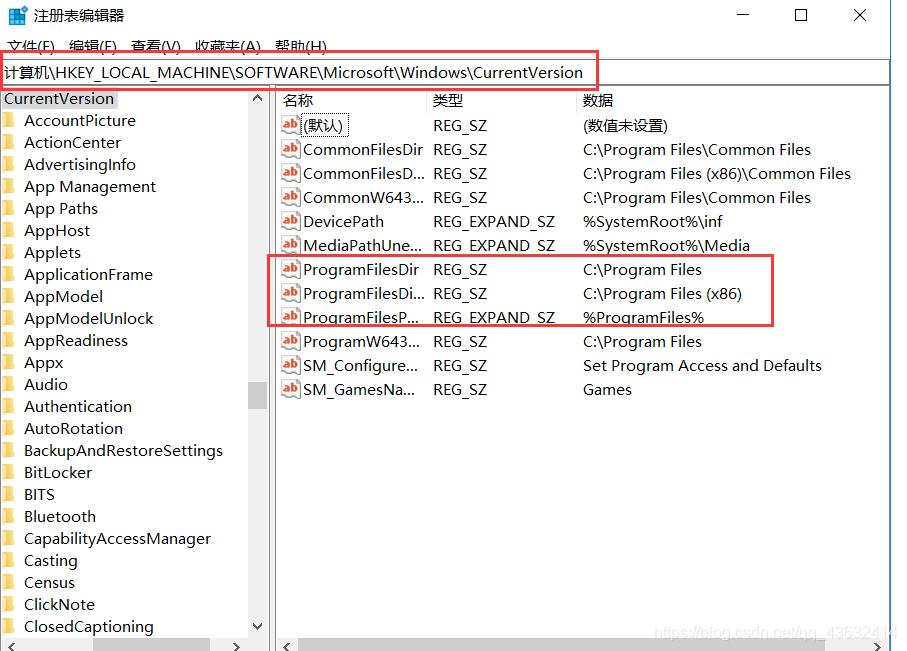
针对 Windows 10 的功能更新,版本 22H2 - 错误 0xc1900204
最近想帮女朋友生win11发现她电脑安装更新总是卡到安装%10这里失败 原来是安装路径被修改过了,改回c盘 win R → 输入regedit 计算机\HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion...
goframe框架规范限制(but it should be named with “Res“ suffix like “XxxRes“)
背景: 首页公司最近要启动一个项目,公司主要业务是用java开发的,但是目前这个方向的项目,公司要求部署在主机上,就是普通的一台电脑上,电脑配置不详,还有经常开关机,所以用java面临…...

格式化选NTFS还是exFAT 格式化NTFS后Mac不能用怎么办 移动硬盘格式化ntfs和exfat的区别
面对硬盘、U盘或移动硬盘的格式化决策,NTFS与exFAT作为主流的文件系统,用户在选择时可以根据它们的不同特点来选择适用场景。下面我们来看看格式化选NTFS还是exFAT,格式化NTFS后Mac不能用怎么办的相关内容。 一、格式化选NTFS还是exFAT 在数…...

中国桥梁空间分布数据
2020年中国桥梁空间分布数据,共包含102000余条数据。 数据属性表包括:地级市名、区县名、桥梁名称和经纬度。有shp和EXCEl两种格式数据。目前暂没有广西、广东和台湾三个省份数据。...

14-15 为什么我们现在对阅读如此难以接受
写出来感觉很奇怪,但最近我感觉自己失去了阅读能力。长篇文本对我来说尤其具有挑战性。句子很难读完。更别提章节了。章节有很多段落,而段落又由许多句子组成。 啊。 即使在极少数情况下,我读完了一章,下一页上已经有另一章等着…...
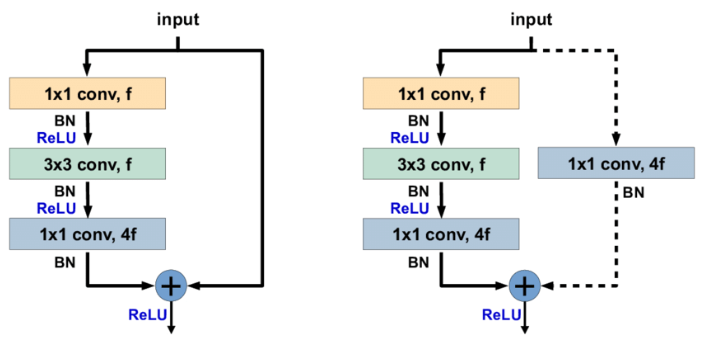
经典的卷积神经网络模型 - ResNet
经典的卷积神经网络模型 - ResNet flyfish 2015年,何恺明(Kaiming He)等人在论文《Deep Residual Learning for Image Recognition》中提出了ResNet(Residual Network,残差网络)。在当时,随着…...

【Git 学习笔记】1.3 Git 的三个阶段
1.3 Git 的三个阶段 由于远程代码库后续存在新的提交,因此实操过程中的结果与书中并不完全一致。根据书中 HEAD 指向的 SHA-1:34acc370b4d6ae53f051255680feaefaf7f7850d,可通过以下命令切换到对应版本,并新建一个 newdemo 分支来…...

华为DCN之:SDN和NFV
1. SDN概述 1.1 SDN的起源 SDN(Software Defined Network)即软件定义网络。是由斯坦福大学Clean Slate研究组提出的一种新型网络创新架构。其核心理念通过将网络设备控制平面与数据平面分离,从而实现了网络控制平面的集中控制,为…...
黑马头条-数据管理平台
目录 项目准备 验证码登录 验证码登录-流程 token 的介绍 个人信息设置和 axios 请求拦截器 axios 响应拦截器和身份验证失败 优化-axios 响应结果 发布文章-富文本编辑器 项目准备 技术: • 基于 Bootstrap 搭建网站标签和样式 • 集成 wangEditor 插件…...

API Object设计模式
API测试面临的问题 API测试由于编写简单,以及较高的稳定性,许多公司都以不同工具和框架维护API自动化测试。我们基于seldom框架也积累了几千条自动化用例。 •简单的用例 import seldomclass TestRequest(seldom.TestCase):def test_post_method(self…...

Python 爬虫:多进程,多线程爬虫<提高爬取效率>
关于多进程,多线程的知识,请自行查询资料补充 ~~~~~~~~~~~ 使用多进程: 在python中,使用多进程需要先导包: from threding import Threaddef work(name):for i in range(1000):print(f"我是线程:{n…...
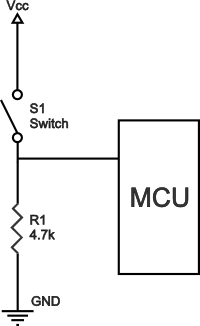
什么是上拉电阻器?上拉和下拉电阻的典型应用
什么是上拉电阻器? 上拉电阻是逻辑电路中使用的电阻,用于确保引脚在所有条件下具有明确定义的逻辑电平。提醒一下,数字逻辑电路有三种逻辑状态:高、低和浮动(或高阻抗)。当引脚未被拉至高或低逻辑电平&…...

centos7安装python3.10
文章目录 1. 安装依赖项2. 下载Python 3.10源码3. 解压源码并进入目录4. 配置安装选项5. 编译并安装Python6. 验证安装7.创建软连接8. 安装pip39. 换源 1. 安装依赖项 sudo yum groupinstall -y "Development Tools" sudo yum install -y openssl-devel bzip2-devel…...

QT事件处理及实例(鼠标事件、键盘事件、事件过滤)
这篇文章通过鼠标事件、键盘事件和事件过滤的三个实例介绍事件处理的实现。 鼠标事件及实例 鼠标事件包括鼠标的移动、按下、松开、单击和双击等。 创建一个MouseEvent项目,通过项目介绍如何获得和处理鼠标事件。程序效果如下图所示。 界面布局代码如下ÿ…...

职场新人必备待办工具 高效待办工作更省心
作为一名初入职场的菜鸟,我曾被繁琐的工作任务压得喘不过气。每天,邮件、会议、项目任务像潮水般涌来,我常常感到力不从心,生怕遗漏了什么重要事项。那种焦虑,就像站在人来人往的地铁站,却不知道自己该搭乘…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
