【Python实战因果推断】20_线性回归的不合理效果10
目录
Neutral Controls
Noise Inducing Control
Feature Selection: A Bias-Variance Trade-Off
Neutral Controls
现在,您可能已经对回归如何调整混杂变量有了一定的了解。如果您想知道干预 T 对 Y 的影响,同时调整混杂变量 X,您所要做的就是在模型中加入 X。或者,为了得到完全相同的结果,您可以根据 X 预测 T,得到残差,并将其作为干预的去势版本。在 X 固定不变的情况下,将 Y 与这些残差进行回归,就能得到 T 与 Y 的关系。
但 X 中应包含哪些变量呢?同样,并不是因为增加变量就能调整变量,所以你想在回归模型中包含所有变量。你不想包含共同效应(对撞机)或中介变量,因为这些变量会引起选择偏差。但在回归中,您还应该了解更多类型的控制因素。这些控制项乍看起来似乎无害,但实际上却相当有害。这些控制被称为中性控制,因为它们不会影响回归估计的偏差。但它们会对方差产生严重影响。正如您所看到的,在回归中包含某些变量时,需要权衡偏差和方差。例如,请考虑下面的 DAG:

您是否应该在模型中加入 credit_score2?如果不包括它,就会得到一直以来看到的相同结果。这个结果是无偏的,因为您是根据信用评分 1_buckets 进行调整的。但是,尽管您不需要这样做,请看看如果您将 credit_score2 计算在内会发生什么。将下面的结果与您之前得到的不包含 credit_score2 的结果进行比较。有什么变化?
formula = "default~credit_limit+C(credit_score1_buckets)+credit_score2"model = smf.ols(formula, data=risk_data_rnd).fit()model.summary().tables[1]首先,关于信贷限额的参数估计值变高了一些。但更重要的是,标准误差减小了。这是因为 credit_score2 对结果 Y 有很好的预测作用,它将有助于线性回归的去噪步骤。在 FWL 的最后一步,由于包含了 credit_score2,Y 的方差将减小,对 T 进行回归将得到更精确的结果。
这是线性回归的一个非常有趣的特性。它表明,线性回归不仅可以用来调整混杂因素,还可以用来减少噪音。例如,如果您的数据来自适当随机化的 A/B 测试,您就不需要担心偏差问题。但您仍然可以使用回归作为降噪工具。只需包含对结果有高度预测性的变量(并且不会引起选择偏差)即可。
Noise Inducing Control
就像控制可以减少噪音一样,它们也可以增加噪音。例如,再次考虑条件随机实验的情况。但这次,您感兴趣的是信用额度对消费的影响,而不是对风险的影响。和上一个例子一样,信用额度是随机分配的,给定的是 credit_score1。但这次,我们假设credit_score1 不是混杂因素。它是干预的原因,但不是结果的原因。这个数据生成过程的因果图如下所示:

这意味着您不需要对credit_score1 进行调整,就能得到信用额度对消费的因果效应。单变量回归模型就可以了。在这里,我保留了平方根函数,以考虑干预反应函数的凹性:
spend_data_rnd = pd.read_csv("data/spend_data_rnd.csv")model = smf.ols("spend ~ np.sqrt(credit_limit)",data=spend_data_rnd).fit()model.summary().tables[1]
但是,如果你确实包括了credit_score1_buckets,会发生什么呢?
model = smf.ols("spend~np.sqrt(credit_limit)+C(credit_score1_buckets)",data=spend_data_rnd).fit()model.summary().tables[1]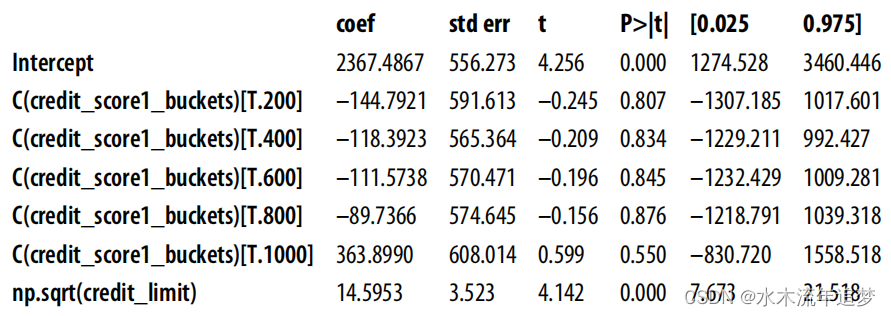 您可以看到,它增加了标准误差,扩大了因果参数的置信区间。这是因为,OLS 喜欢干预方差大的情况。但是如果控制了一个可以解释干预的协变量,就会有效地降低干预的方差。
您可以看到,它增加了标准误差,扩大了因果参数的置信区间。这是因为,OLS 喜欢干预方差大的情况。但是如果控制了一个可以解释干预的协变量,就会有效地降低干预的方差。
Feature Selection: A Bias-Variance Trade-Off
在现实中,很难出现协变量导致干预而不导致结果的情况。最有可能出现的情况是,有很多混杂因素同时导致 T 和 Y,只是程度不同而已。在图 中,X1 是 T 的强致因,但 Y 的弱致因;X3 是 Y 的强致因,但 T 的弱致因;X2 处于中间位置,如每个箭头的粗细所示。
在这种情况下,您很快就会陷入进退两难的境地。一方面,如果您想摆脱所有偏差,就必须包括所有协变量;毕竟,它们是需要调整的混杂因素。另一方面,对干预原因进行调整会增加你的估计器的方差。
为了了解这一点,让我们根据图 中的因果图来模拟数据。这里,真实的 ATE 是 0.5。如果您试图在控制所有混杂因素的情况下估计这一效应,估计值的标准误差会过高,无法得出任何结论。
np.random.seed(123)n = 100(x1, x2, x3) = (np.random.normal(0, 1, n) for _ in range(3))t = np.random.normal(10*x1 + 5*x2 + x3)# ate = 0.05y = np.random.normal(0.05*t + x1 + 5*x2 + 10*x3, 5)df = pd.DataFrame(dict(y=y, t=t, x1=x1, x2=x2, x3=x3))smf.ols("y~t+x1+x2+x3", data=df).fit().summary().tables[1]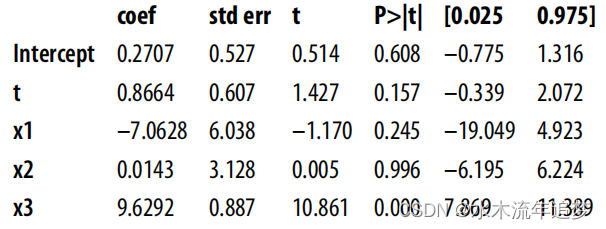
如果您知道其中一个混杂因素对干预的预测作用很强,而对结果的预测作用很弱,您可以选择将其从模型中剔除。在本例中,这就是 X1。现在,请注意!这将使您的估计出现偏差。但是,如果这也能显著降低方差,也许这就是值得付出的代价:
smf.ols("y~t+x2+x3", data=df).fit().summary().tables[1]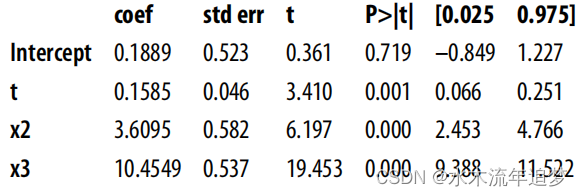
底线是,在模型中包含(调整)的混杂因素越多,因果关系估计值的偏差就越小。但是,如果您包含的变量对干预结果的预测作用较弱,但对治疗的预测作用较强,那么这种偏差的减少将以方差的增加为代价。同理可证,有时为了减少方差而接受一点偏差是值得的。此外,您应该非常清楚,并非所有的混杂因素都是相同的。当然,因为 T 和 Y 的关系,所有的混杂因素都是常见的。但如果它们对治疗的解释太多,而对干预结果的解释几乎没有,那么你真的应该考虑将其从调整中剔除。这适用于回归,但也适用于其他调整策略,如倾向得分加权。
遗憾的是,混杂因素对干预的解释能力应该有多弱,才能证明剔除它是合理的,这在因果推理中仍是一个未决问题。不过,这种偏差与方差的权衡还是值得了解的,因为它有助于您理解和解释线性回归的情况。
相关文章:

【Python实战因果推断】20_线性回归的不合理效果10
目录 Neutral Controls Noise Inducing Control Feature Selection: A Bias-Variance Trade-Off Neutral Controls 现在,您可能已经对回归如何调整混杂变量有了一定的了解。如果您想知道干预 T 对 Y 的影响,同时调整混杂变量 X,您所要做的…...

在Ubuntu 16.04上安装和配置ownCloud的方法
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 简介 ownCloud 是一个文件共享服务器,允许您将个人内容(如文档和图片)存储在一个类似 Dropbox 的集…...

Java | Leetcode Java题解之第213题打家劫舍II
题目: 题解: class Solution {public int rob(int[] nums) {int length nums.length;if (length 1) {return nums[0];} else if (length 2) {return Math.max(nums[0], nums[1]);}return Math.max(robRange(nums, 0, length - 2), robRange(nums, 1,…...

使用 ESP32 接收 MAX4466 模拟麦克风模块的数据,通过 DAC 转码成 PCM 格式,并通过 MQTT 发送给另一台设备,可以通过以下步骤实现。
硬件准备 两个 ESP32 开发板MAX4466 模拟麦克风模块MQTT 服务器(例如 Mosquitto) 接线 MAX4466 模块输出(AO) -> ESP32 ADC 引脚(如 GPIO 34) 软件准备 音频采集DAC 转码MQTT 发送和接收 代码实现…...
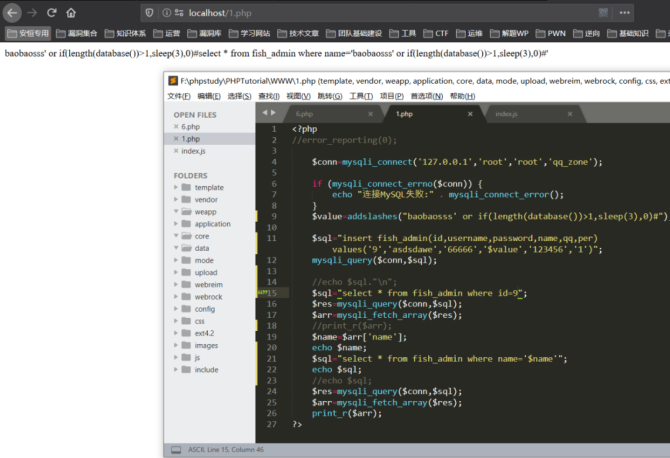
SQL二次注入原理分析
二次注入在测试的时候比较少见,或者说很难被测出来,因为测的时候首先要去找注入的位置,其次是去判断第一次执行的SQL语句,然后还要去判断第二次进行调用的 SQL 语句。而关键问题就出在第二次的调用上面。 下面以一个常用过滤方法…...
在线签约如何选择?2024年10款顶级app大比拼
支持电子合同签约的10大app:e签宝、上上签、DocuSign、契约锁、Adobe Sign、法大大、SignNow、安心签、HelloSign、PandaDoc。 无论是企业之间的交易还是个人服务合同,线上电子合同签约提供了一种便捷、高效且安全的方式来处理法律文档。本文将介绍几款优…...

gcc: warning: -Wunused-function;加了选项,为什么就不报警告呢?
文章目录 问题clang的编译而使用gcc是就不报问题分析原因如果是非static的函数问题 下面这个代码段,其中这个函数hton_ext_2byte,在整个程序里就没有使用。 static inline uint16_t hton_ext_2byte(uint8_t **p) {uint16_t v;******return v;...

系统提示我未定义与 ‘double‘ 类型的输入参数相对应的函数 ‘finverse‘,如何解决?
🏆本文收录于「Bug调优」专栏,主要记录项目实战过程中的Bug之前因后果及提供真实有效的解决方案,希望能够助你一臂之力,帮你早日登顶实现财富自由🚀;同时,欢迎大家关注&&收藏&&…...

【电路笔记】-B类放大器
B类放大器 文章目录 B类放大器1、概述2、B类放大器介绍3、推挽式配置4、限制交叉失真5、B类放大器效率6、总结1、概述 我们在之前的文章中已经知道,A 类放大器的特点是导通角为 360,理论最大效率为 50%。 在本文中,我们将详细介绍另一类放大器,称为B类放大器,它是为解决A…...
Ubuntu 22.04 安装中文字体
笔者在用OpenCV4.9处理图片加水印时,中文乱码。原来是Ubuntu 22.04发行版缺少中文字体支持,因此,笔者就找资料安装了需要的中文字体,特此记录,以备后查。 1、打开终端: 2、更新软件包列表: su…...

「树莓派入门」树莓派进阶04-直流电机控制与PWM应用
直流电机控制是树莓派硬件项目中的一项重要技能。通过PWM技术,你可以实现对电机速度的精确控制。在实验过程中,请注意电机的电源匹配和GPIO引脚的保护。 一、直流电机基本原理 直流电机通过直流电源供电,其工作原理基于洛伦兹力定律,即电流通过线圈时,会在磁场中受到力的…...

利用数据集,用机器学习模型对股市预测,聊聊看!
🏆本文收录于「Bug调优」专栏,主要记录项目实战过程中的Bug之前因后果及提供真实有效的解决方案,希望能够助你一臂之力,帮你早日登顶实现财富自由🚀;同时,欢迎大家关注&&收藏&&…...

015-GeoGebra基础篇-定点旋转物体、动态显示数值并显示运动轨迹
这可能是我能想到的最大概率可以被你搜索到的标题了,容我先喘口气~ 目录 一、成品展示二、涉及内容三、做图步骤(1)绘制三角形t(2)建立定点D(3)制作角度滑动条(4)图形绕点…...

2024年6月份找工作和面试总结
转眼间6月份已经过完了,2024年已经过了一半,希望大家都找到了合适的工作。 本人前段时间写了5月份找工作的情况,请查看2024年5月份面试总结-CSDN博客 但是后续写的总结被和谐了,不知道这篇文章能不能发出来。 1、6月份面试机会依…...

同步时钟:北斗/GPS卫星、电信基站、NTP以太网校时方式的区别
同步时钟是保证各设备时间统一的重要装置,广泛应用于电力、通信、金融、学校、医院、地铁等多个领域。目前,常用的同步时钟方式包括:北斗/GPS卫星、电信基站、NTP以太网等。 下面跟着小编来看一下这些校时方式及他们的区别吧。 1. 北斗/GP…...

实现Java应用的快速开发与迭代
实现Java应用的快速开发与迭代 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 1. 引言 随着软件开发周期的不断缩短和市场竞争的加剧,快速开发和…...
利用redis数据库管理代理库爬取cosplay网站-cnblog
爬取cos猎人 数据库管理主要分为4个模块,代理获取模块,代理储存模块,代理测试模块,爬取模块 cos猎人已经倒闭,所以放出爬虫源码 api.py 为爬虫评分提供接口支持 import requests import concurrent.futures import …...

数据仓库建模基础理论-01-为什么需要数据建模?
一、什么是数据模型? 数据模型是数据库的基础结构,用于描述和组织数据的方式。 它不仅是数据库的底层结构,还是一个概念性工具,帮助理解数据的含义和关系。 数据模型包括数据本身、数据之间的关系、数据的语义(含义和…...
中序遍历的两种实现——二叉树专题复习
递归实现: /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val val; }* TreeNode(int val, TreeNode left, TreeNode right)…...

python 基础综合应用——小开发
#python 基础综合应用——小开发 综合复习 变量- 循环- 函数- 模块 开发 名片管理系统 名片管理系统介绍 名片管理系统可以理解成花名册软件,通过个人新建人的信息后可以进行查询等简单操作的程序 名片管理系统有三个作用, 1.新建名片 2.显示全部名…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

