【2023unity游戏制作-mango的冒险】-3.基础动作和动画API实现

👨💻个人主页:@元宇宙-秩沅
hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅!
本文由 秩沅 原创
收录于专栏:unity游戏制作
⭐mango的基础动作动画的添加⭐
文章目录
- ⭐mango的基础动作动画的添加⭐
- 👨💻前言
- 👨💻场景搭建
- 🎶音频添加
- 🎶mango的移动和动画
- 😁实现效果:
- 😁实现步骤:
- 🎶mango的跳跃和动画
- 😁实现效果:
- **💕重点细节**:
- 😁实现步骤:
- 🎶整体代码2
- ⭐相关文章⭐
👨💻前言
🎶版本: 为 Ltp 2021年版本的unity
🎶类型: 简单2D类冒险游戏
🎶目的: 熟悉掌握基本unityAPI
🎶视频教程:【2023小白狂飙unity2D冒险类游戏制作【mango的冒险】】
👨💻场景搭建

- 需要注意的重点
- 渲染层级的关系
🎶音频添加
音频资源直接去unity的商店里下载免费的资源即可
- 添加下图圈出的组件名

🎶mango的移动和动画
😁实现效果:
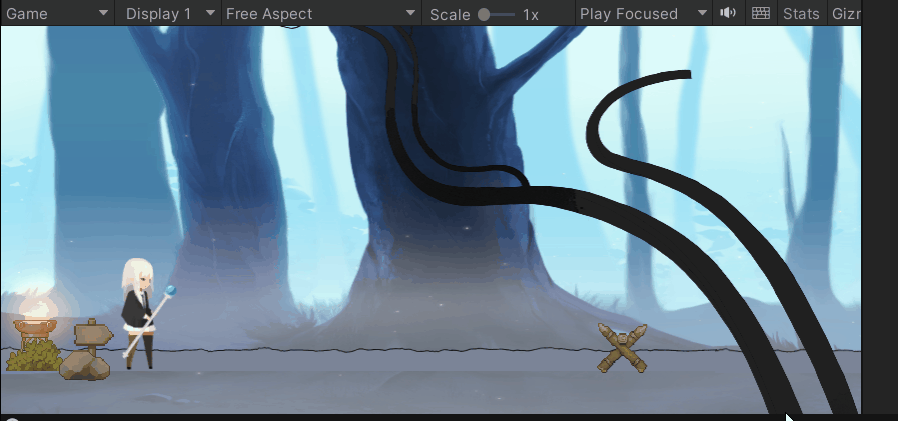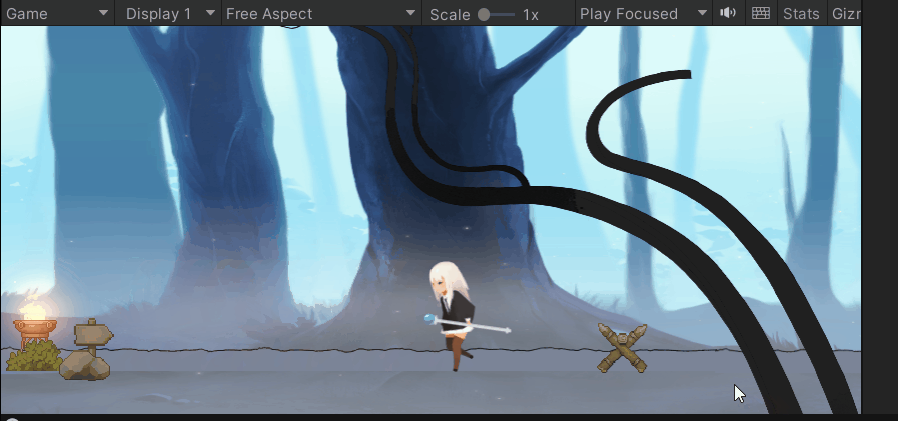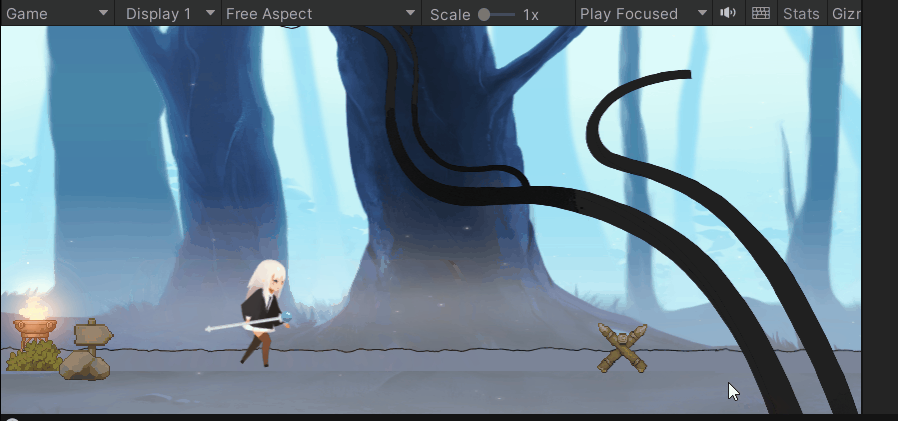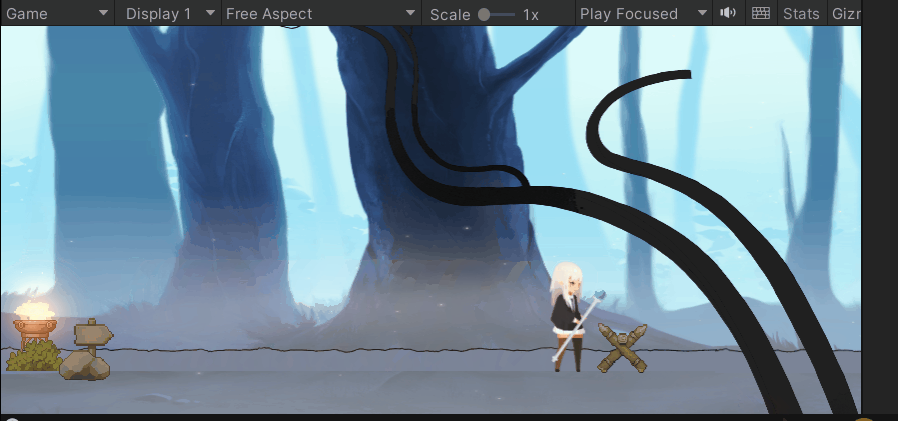
😁实现步骤:
- 1.确定–移动的实现是通过刚体力的牵引
mango添加RigidBody2D组件 - 2.添加地形碰撞器


- 3. 通过刚体组件实现物体的移动,我们只需要将刚体速度的大小和方向进行赋值即可
细节:勾选Freeze Rotation Z
作用:不会倾倒
//通过刚体组件实现物体的移动,我们只需要将刚体速度的大小和方向进行赋值即可//mangoMovex 和 mangoMoveY 都是vector2 类型的变量mangoMovex = Vector2.right * x * SpeedVauel; //x轴的速度mangoMovey = new Vector2(0, Rmango.velocity.y); //y轴的速度//速度向量的合成,有大小并且有方向的Rmango.velocity = mangoMovex + mangoMovey;
// 效果: 可以进行移动,但是方向不变,定向的,
- 4.添加移动的动画
MGanimator.SetFloat("Run", Mathf.Abs(Rmango .velocity .x));
- 5.实现转向和移动动画相契合
| 转向的三种方法 | 注释 |
|---|---|
| Rotation | 180度旋转 |
| Scale | 正负的切换 |
| Flip | 勾选 |
if (x > 0){transform.rotation = new Quaternion(0, 0, 0, 0);}else if (x < 0){transform.rotation = new Quaternion(0, 180, 0, 0);}🎶mango的跳跃和动画
😁实现效果:
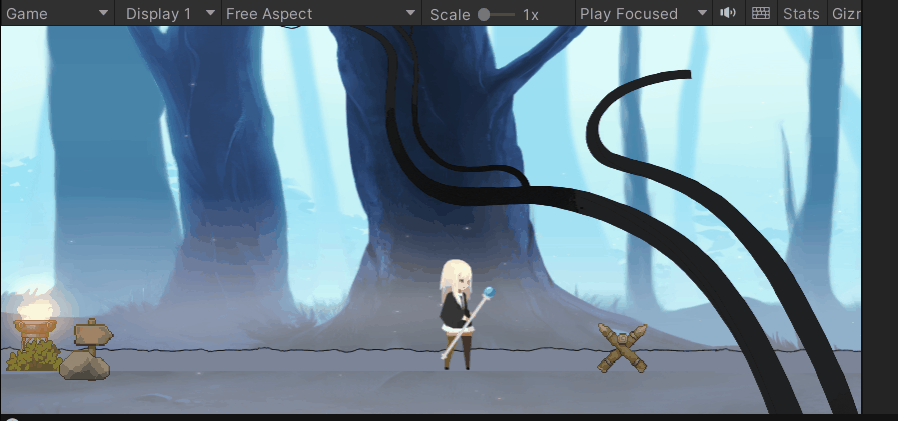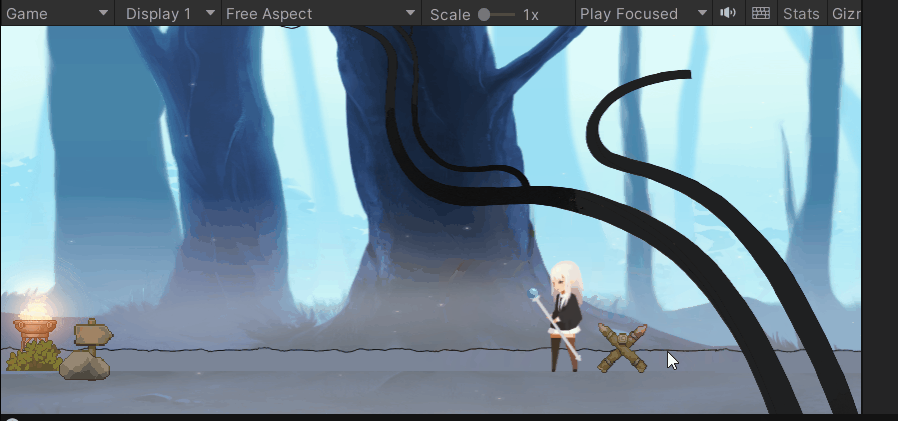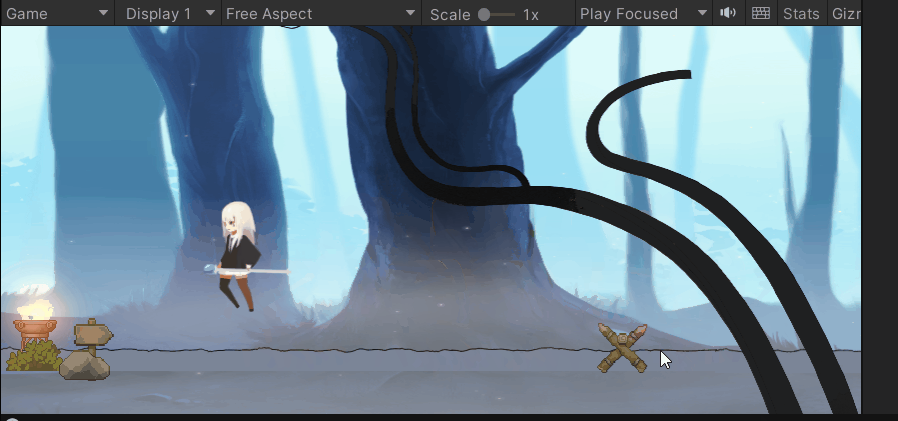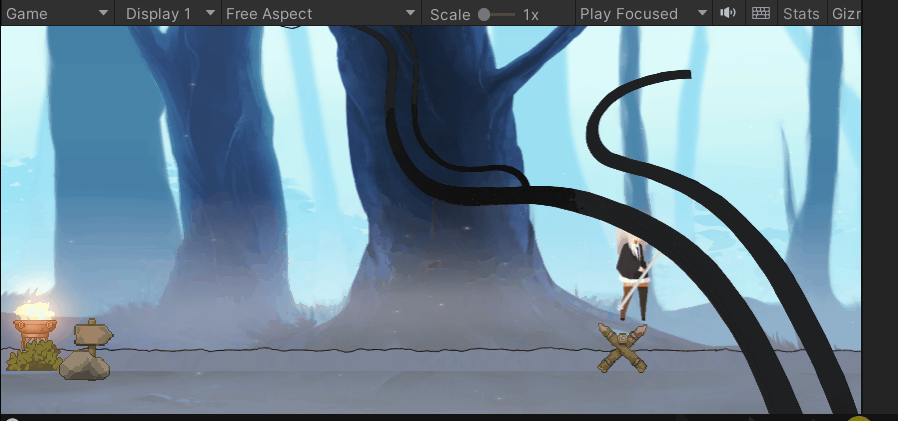
💕重点细节:
- 动画之间切换不流畅(空中播放奔跑的动画)
- 跳不起来,跳太高,重复跳
- 逻辑不顺畅导致的错误
- 动画播放的快慢的控制
😁实现步骤:
- 1.给动画机添加跳跃动画Jump
- 2.当按下空格的时候,实现跳跃的动作
- 3.在跳跃时不播放奔跑动画也不播放静止动画
- 4.向上拉的力能否将物体拉动,并且下降是否连贯
(做牵引力运动要考虑力和质量还有重力的关系)
动画的逻辑:
奔跑动画在跳跃状态时才切换到跳跃动画
禁止状态在跳跃状态时也切换到跳跃动画
🎶整体代码2
using System.Collections;
using System.Collections.Generic;
using UnityEditor.Rendering;
using UnityEngine;//-----------------------
//--作用:mango的移动
//-----------------------
public class mangoMove : MonoBehaviour
{// Start is called before the first frame updateprivate float x;private float y;private Rigidbody2D Rmango;private Vector2 mangoMovex,mangoMovey;private float SpeedVauel = 5;public float JumpSpeed = 1000;private Animator MGanimator;private bool isGrounp;void Start(){Rmango = GetComponent<Rigidbody2D>();MGanimator = GetComponent<Animator>();}private void Update(){x = Input.GetAxis("Horizontal"); // 按AD键获取类型为Float的数值作为系数范围为【-1,1】//当按下A的时候 x是负数 ,按下D的时候x是正数if (x > 0){transform.rotation = new Quaternion(0, 0, 0, 0);}else if (x < 0){transform.rotation = new Quaternion(0, 180, 0, 0);}//当按下空格键和 符合 在地面的条件时if ( Input.GetButtonDown ("Jump") && isGrounp ) { Rmango.AddForce(Vector2.up * JumpSpeed );MGanimator.SetBool("Jump", true);}else if( isGrounp == true ){MGanimator.SetBool("Jump", false );}}void FixedUpdate(){Move();}private void Move(){//通过刚体组件实现物体的移动,我们只需要将刚体速度的大小和方向进行赋值即可//mangoMovex 和 mangoMoveY 都是vector2 类型的变量mangoMovex = Vector2.right * x * SpeedVauel; //x轴的速度mangoMovey = new Vector2(0, Rmango.velocity.y); //y轴的速度//速度向量的合成,有大小并且有方向的Rmango.velocity = mangoMovex + mangoMovey;if (isGrounp == true ) //是否在地面上{MGanimator.SetFloat("Run", Mathf.Abs(Rmango .velocity .x));}else{MGanimator.SetFloat("Run", 0);}}//碰撞器方法private void OnCollisionEnter2D(Collision2D collision){isGrounp =collision . gameObject.CompareTag("grounp");Debug.Log(" " + isGrounp);}private void OnCollisionExit2D(Collision2D collision) //也可以说是跳跃状态的时候{isGrounp = false;Debug.Log(" " + isGrounp);}
}🎶🎶我们继续后面的制作。
⭐相关文章⭐
⭐【2023unity游戏制作-mango的冒险】-2.开始画面API制作
⭐【unity游戏制作-mango的冒险】-1.场景搭建
⭐“狂飙”游戏制作—游戏分类图鉴(网易游学)
⭐本站最全-unity常用API大全(万字详解),不信你不收藏
你们的点赞👍 收藏⭐ 留言📝 关注✅是我持续创作,输出优质内容的最大动力!
相关文章:

【2023unity游戏制作-mango的冒险】-3.基础动作和动画API实现
👨💻个人主页:元宇宙-秩沅 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 秩沅 原创 收录于专栏:unity游戏制作 ⭐mango的基础动作动画的添加⭐ 文章目录⭐mango的基础动作动画的添加⭐…...

跨域的几种解决方案?
1-jsonp 【前端后端实现】jsonp: 利用 <script> 标签没有跨域限制的漏洞,网页可以得到从其他来源动态产生的 JSON 数据。JSONP请求一定需要对方的服务器做支持才可以。JSONP优点是简单兼容性好,可用于解决主流浏览器的跨域数据访问的问题。缺点是仅…...

2022年山东省职业院校技能大赛网络搭建与应用赛项正式赛题
2022年山东省职业院校技能大赛 网络搭建与应用赛项 第二部分 网络搭建与安全部署&服务器配置及应用 竞赛说明: 一、竞赛内容分布 竞赛共分二个模块,其中: 第一模块:网络搭建及安全部署项目 第二模块:服务…...
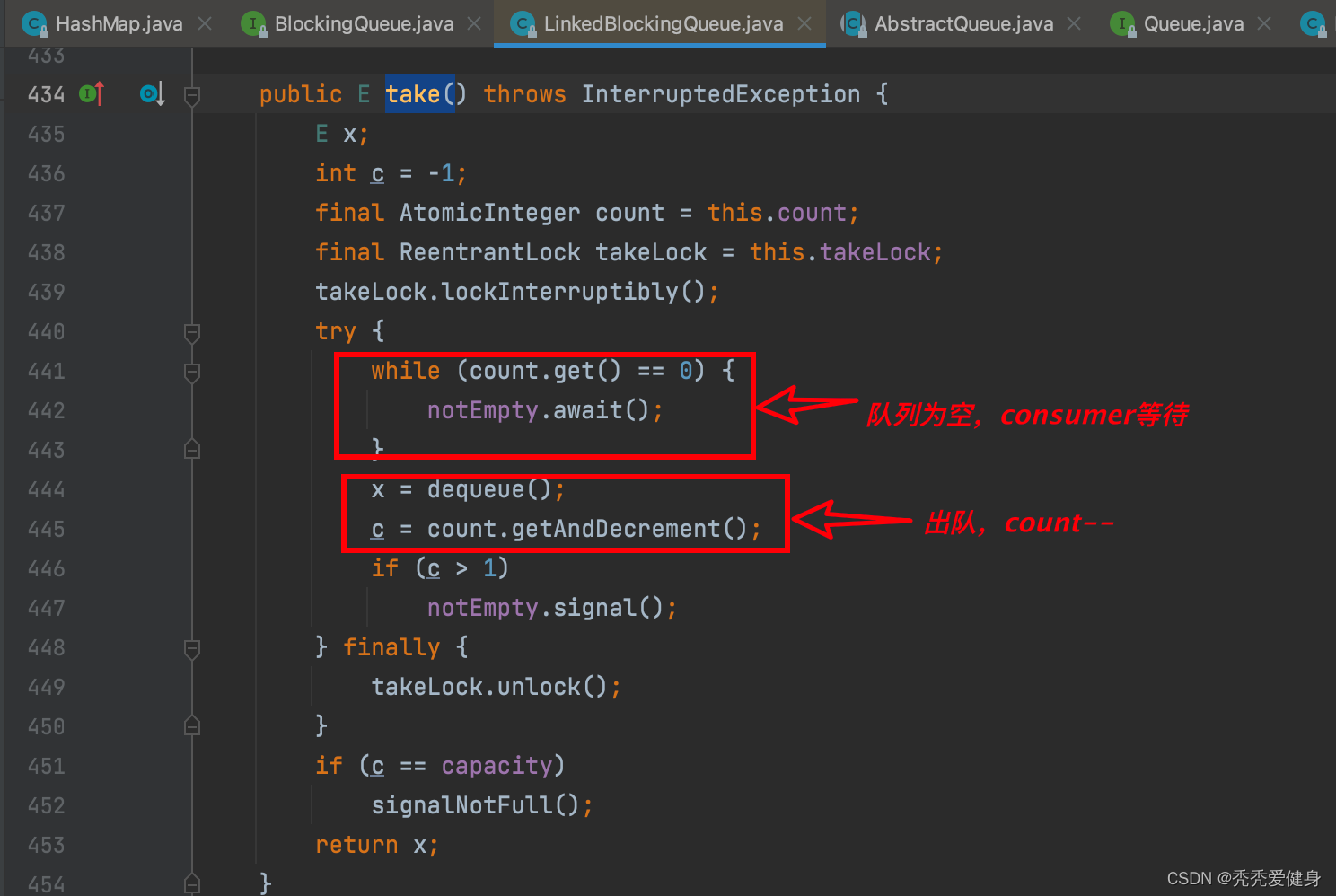
【JUC并发编程】ArrayBlockingQueue和LinkedBlockingQueue源码2分钟看完
文章目录1、BlockingQueue1)接口方法2)阻塞队列分类2、ArrayBlockingQueue1)构造函数2)put()入队3)take()出队3、LinkedBlockingQueue1)构造函数2)put()入队3)take()出队1、Blocking…...
GitHub个人资料自述与管理主题设置
目录 关于您的个人资料自述文件 先决条件 添加个人资料自述文件 删除个人资料自述文件 管理主题设置 补充:建立一个空白文件夹 关于您的个人资料自述文件 可以通过创建个人资料 README,在 GitHub.com 上与社区分享有关你自己的信息。 GitHub 在个…...

Express篇-连接mysql
创建数据库配置文件config/sqlconfig.jsconst sqlconfig {host: localhost, // 连接地址user: root, //用户名password: ****, //密码port: 3306 , //端口号database: mysql01_dbbooks //数据库名 } module.exports sqlconfig封装数据库管理工具 utils/mysqlUtils.…...
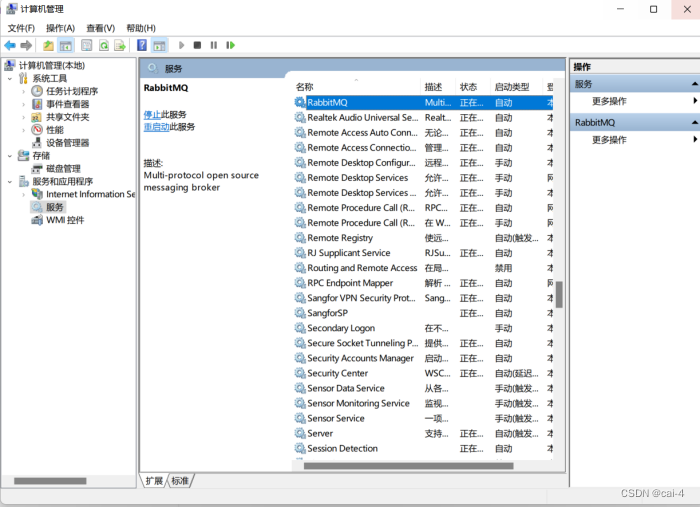
win10 安装rabbitMQ详细步骤
win10 安装rabbitMQ详细步骤 win10 安装rabbitMQ详细步骤win10 安装rabbitMQ详细步骤一、下载安装程序二、安装配置erlang三、安装rabbitMQ四、验证初始可以通过用户名:guest 密码guest来登录。报错:安装RabbitMQ出现Plugin configuration unchanged.问题…...
【成为架构师课程系列】一线架构师:6个经典困惑及其解法
目录 一线架构师:6个经典困惑及其解法 多阶段还是多视图? 内置最佳实践 架构方法论:3个阶段,一个贯穿 Pre-architecture阶段:ADMEMS矩阵方法 Conceptual Architecture阶段:重大需求塑造做概念架构 Refined Architecture…...
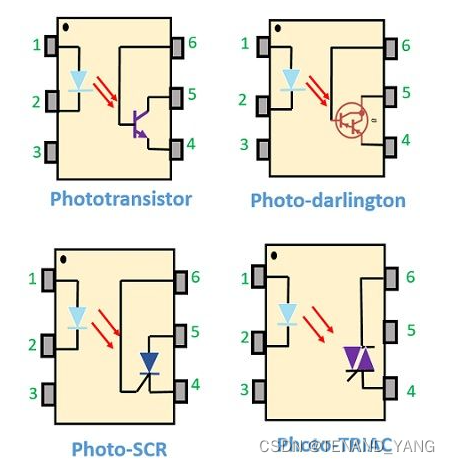
光耦合器的定义与概述
光耦合器或光电耦合器是一种电子元件,基本上充当具有不同电压电平的两个独立电路之间的接口。光耦合器是可在输入和输出源之间提供电气隔离的常用元件。它是一个 6 引脚器件,可以有任意数量的光电探测器。 在这里,光源发出的光束作为输入和输…...
谷粒商城--品牌管理详情
目录 1.简单上传测试 2.Aliyun Spring Boot OSS 3.模块mall-third-service 4.前端 5.数据校验 6.JSR303数据校验 7.分组校验功能 8.自定义校验功能 9.完善代码 1.简单上传测试 OSS是对象存储服务,有什么用呢?把图片存储到云服务器上能让所有人…...

stack、queue和priority_queue
目录 一、栈(stack) 1.stack的使用 2.容器适配器 3.stack的模拟实现 二、队列(queue) 1.queue的使用 2.queue的模拟实现 三、双端队列(deque) 1.vector,list的优缺点 2.认识deque 四…...
面试题(二十二)消息队列与搜索引擎
2. 消息队列 2.1 MQ有什么用? 参考答案 消息队列有很多使用场景,比较常见的有3个:解耦、异步、削峰。 解耦:传统的软件开发模式,各个模块之间相互调用,数据共享,每个模块都要时刻关注其他模…...
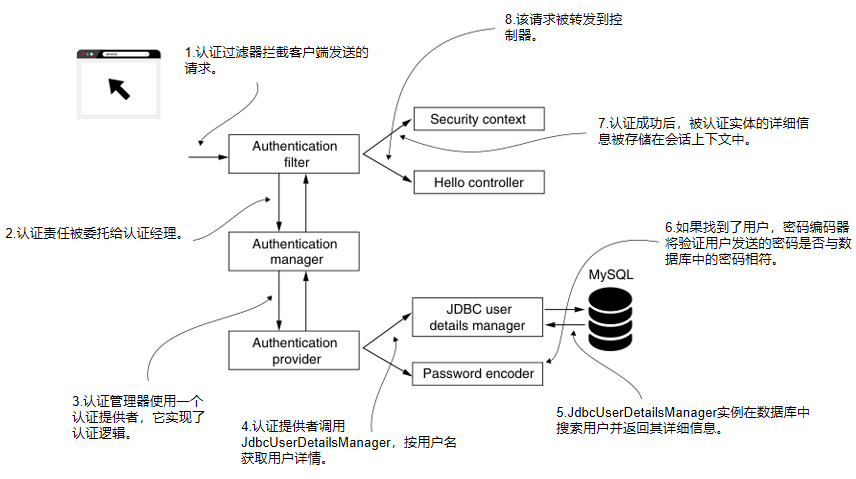
Spring Security in Action 第三章 SpringSecurity管理用户
本专栏将从基础开始,循序渐进,以实战为线索,逐步深入SpringSecurity相关知识相关知识,打造完整的SpringSecurity学习步骤,提升工程化编码能力和思维能力,写出高质量代码。希望大家都能够从中有所收获&#…...

Java面试——maven篇
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

基于微信小程序的游戏账号交易小程序
文末联系获取源码 开发语言:Java 框架:ssm JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏览器…...
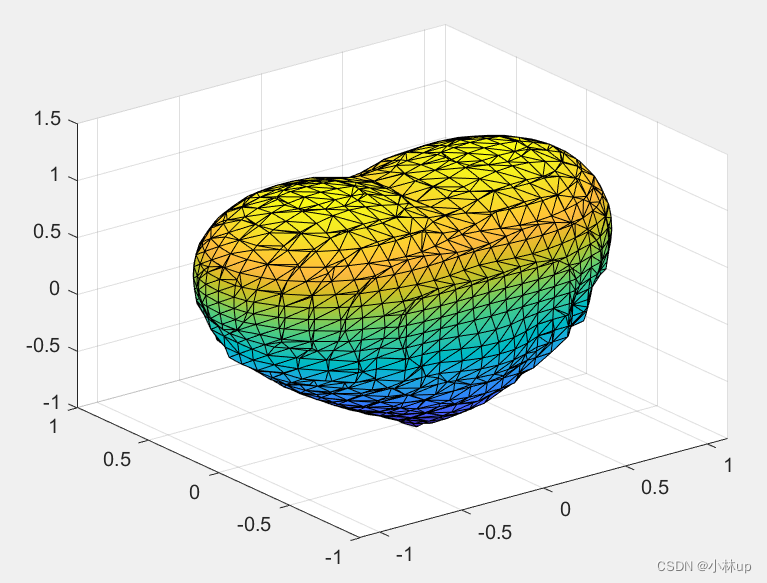
Matlab绘制隐函数总结-二维和三维
1.二维隐函数 二维隐函数满足f(x,y)0f(x,y)0f(x,y)0,这里无法得到yf(x)yf(x)yf(x)的形式。不能通过普通函数绘制。 我们要关注的是使用fplot函数和fimplicit函数。 第1种情况:基本隐函数 基本的隐函数形式形如: x2y22x2(x2y2)12x^{2}y^{…...

如何直观地理解傅立叶变换?频域和时域的理解
如何直观地理解傅立叶变换 傅里叶变换连续形式的傅立叶变换如何直观地理解傅立叶变换?一、傅里叶级数1.1傅里叶级数的三角形式1.2 傅里叶级数的复指数形式二、傅里叶变换2.1一维连续傅里叶变换三、频谱和功率谱3.1频谱的获得3.2频谱图的特征3.3频谱图的组成频域(frequency do…...
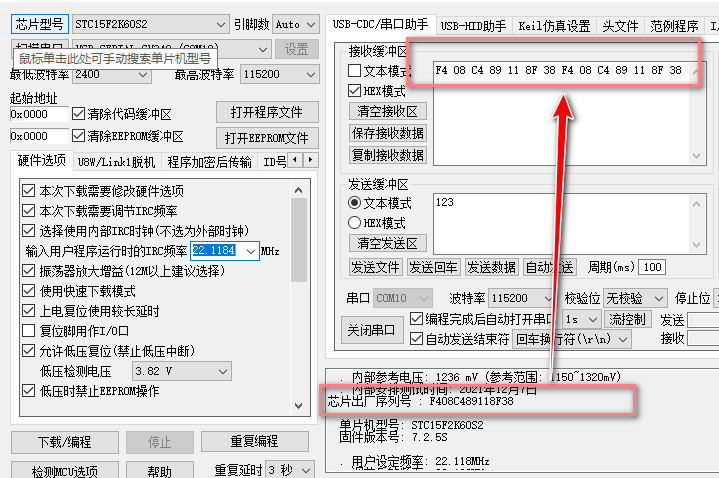
STC15读取内部ID示例程序
STC15读取内部ID示例程序🎉本案例基于STC15F2K60S2为验证对象。 📑STC15 ID序列介绍 STC15系列STC最新一代STC15系列单片机出厂时都具有全球唯一身份证号码(ID号)。最新STC15系列单片机的程序存储器的最后7个字节单元的值是全球唯一ID号,用…...
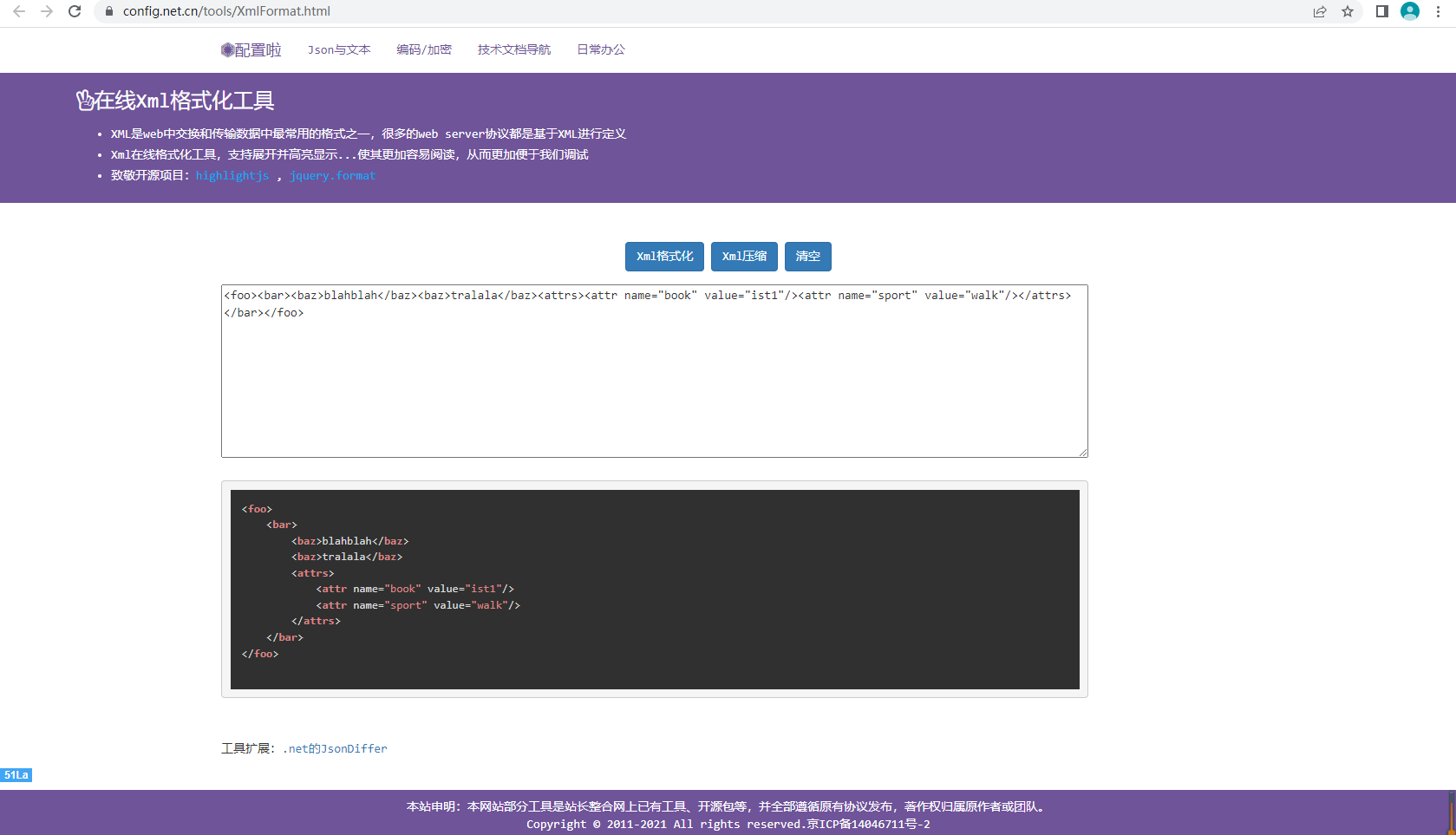
Xml格式化与高亮显示
具体请参考:Xml格式化与高亮显示...

【GlobalMapper精品教程】045:空间分析工具(2)——相交
GlobalMapper提供的空间分析(操作)的方法有:交集、并集、单并集、差异、对称差集、相交、重叠、接触、包含、等于、内部、分离等,本文主要讲述相交工具的使用。 文章目录 一、实验数据二、符号化设置三、相交运算四、结果展示五、心灵感悟一、实验数据 加载配套实验数据(…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
