数字信号处理及MATLAB仿真(2)——离散系统
上回书说到如何来编写一些简单的离散时间序列,今天咱们就来谈谈一些关于常系数差分方程的操作吧。
说到这里咱们对于常系数差分方程可能最关心的就是怎么去求解了。
其中最关键的部分就是filter函数,可以用来计算系统在输入信号为x的输出信号y。大家学过这个函数的可能会有个疑问——filter函数不是一个用来滤波函数吗?对于这个我只能说问的好。因为答案往往就在疑问的背后,其实filter函数的具体工作原理是基于差分方程的数学运算。它根据输入信号x以及系数向量a和b,按照差分方程的规则逐步计算输出信号y的每个样本值。在计算过程中,会考虑输入信号的当前和过去样本值,以及输出信号的过去样本值,以得到符合差分方程关系的输出结果。这种计算方式能够模拟离散系统对输入信号的响应。需要注意的是,在使用filter函数时,要确保a向量的第一个元素不为零,否则需要对b和a的元素进行相应的处理。
来看两个例子吧。一个是一阶的方程求解,还有一个是二阶方程的求解。程序如下。
%差分方程的求解
%差分方程为y[n]-0.5y[n-1]=x[n]。
clear all
clc
% 定义差分方程系数
a = [1, -0.5]; % y[n] 的系数
b = 1; % x[n] 的系数
% 生成输入信号 x[n](这里用正弦波示例)
n = 0:99;
x = sin(2*pi*0.1*n);
% 使用 filter 函数求解差分方程
y = filter(b, a, x);
% 绘制输入信号和输出信号
figure;
subplot(2,1,1);
plot(n, x);
xlabel('n');
ylabel('x[n]');
title('输入信号');
subplot(2,1,2);
plot(n, y);
xlabel('n');
ylabel('y[n]');
title('输出信号');
% 显示差分方程
disp('差分方程:');
disp('y[n] - 0.5y[n-1] = x[n]');
%%
% 定义差分方程系数
a = [1, -1.5, 0.7]; % y[n] 的系数
b = [1, 0.5]; % x[n] 的系数
% 生成输入信号 x[n](这里用正弦波示例)
n = 0:99;
x = sin(2*pi*0.1*n);
% 使用 filter 函数求解差分方程
y = filter(b, a, x);
% 绘制输入信号和输出信号
figure;
subplot(2,1,1);
plot(n, x);
xlabel('n');
ylabel('x[n]');
title('输入信号');
subplot(2,1,2);
plot(n, y);
xlabel('n');
ylabel('y[n]');
title('输出信号');
% 显示差分方程
disp('差分方程:');
disp('y[n] - 1.5y[n-1] + 0.7y[n-2] = x[n] + 0.5x[n-1]');
运行结果:


结果大概就这样了,大家细细比较还是有那么点区别。但是具体一点的区别,大家可以用双零分解的方法去求求,验证一下,理论和实际之间还是有区别的。
接下来看看,单位冲激响应怎么搞,核心是impz函数,在 MATLAB 中,impz函数用于计算并返回数字滤波器的单位冲激响应。差分方程为y[n] - 1.5y[n-1] + 0.7y[n-2] = x[n] + 0.5x[n-1],程序如下图。
%单位冲激响应
%差分方程为y[n] - 1.5y[n-1] + 0.7y[n-2] = x[n] + 0.5x[n-1]
% 定义差分方程系数
a = [1, -1.5, 0.7]; % y[n] 的系数
b = [1, 0.5]; % x[n] 的系数
% 计算单位冲激响应
[h, n] = impz(b, a);
% 绘制单位冲激响应
figure;
stem(n, h);
xlabel('n');
ylabel('h[n]');
title('单位冲激响应');
grid on;
% 显示差分方程
disp('差分方程:');
disp('y[n] - 1.5y[n-1] + 0.7y[n-2] = x[n] + 0.5x[n-1]');
首先,定义了差分方程中与y[n] 的系数 a 和 x[n] 的系数 b 。然后,使用 impz函数计算单位冲激响应 h以及对应的时间索引 n。接下来,通过 stem函数绘制单位冲激响应的图形xlabel 和 ylabel 分别设置了横纵坐标的标签,title 给出了图形的标题,grid on 显示网格。最后,使用 disp 函数显示了定义的差分方程。运行这段代码,将会得到单位冲激响应的图形。结果如下图所示。

今天主要讲的就是离散时间系统,结合例子理解更加的合适。
欲知后事如何,且听下回分解。OVO........
相关文章:

数字信号处理及MATLAB仿真(2)——离散系统
上回书说到如何来编写一些简单的离散时间序列,今天咱们就来谈谈一些关于常系数差分方程的操作吧。 说到这里咱们对于常系数差分方程可能最关心的就是怎么去求解了。 其中最关键的部分就是filter函数,可以用来计算系统在输入信号为x的输出信号y。大家学过…...
技术原理)
大模型思维链(Chain-of-Thought)技术原理
大模型思维链(Chain-of-Thought)技术原理 NLP中 大语言模型LLM中的思维链 Chain-of-Thought(CoT) GoT_cot思维链-CSDN博客 https://zhuanlan.zhihu.com/p/680618940 https://zhuanlan.zhihu.com/p/661475269...
gda动态调试-cnblog
忽的发现gda有动态调试功能 动态监听返回值 框柱指定方法,选择调试方法,gda会自动监听函数的返回值,例如 自定义frida脚本 gda会自动生成hook该函数的frida脚本...

Double 4 VR仿真情景实训教学系统在法律专业课堂上的应用
随着科技的飞速发展,VR技术逐渐渗透到各个领域,为教育行业带来了革命性的变化。 VR技术以其独特的沉浸式体验,为法律课堂带来了前所未有的学习体验。通过Double 4 VR仿真情景实训教学系统,学生可以身临其境地进入虚拟的仿真情景中…...

k8s-第一节-minikube
minikube 服务器启动 # 启动集群 minikube start # 启动集群并使用docker驱动 minikube start --driverdocker To make docker the default driver:minikube config set driver docker # 查看节点。kubectl 是一个用来跟 K8S 集群进行交互的命令行工具 kubectl get node # 停…...

html+js+css在线倒计时
代码在图片后面 点赞加关注 谢谢大佬照顾😜 图例 时间到前 时间到后 源代码 <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta name"viewport" content"widthdevice-width,…...

构建LangChain应用程序的示例代码:55、如何实现多代理模拟,其中特权代理决定谁发言。这遵循与多代理分散发言者选择相反的选择方案
示例展示了如何实现一个多代理模拟,其中一个特权代理决定谁来发言。 这遵循与多代理分散式发言人选择相反的选择方案。 我们在一个虚构的新闻网络模拟环境中展示这种方法的一个例子。这个例子将展示我们如何实现能够: 在说话前思考终止对话 的代理。 导入LangChain相关模块…...

船舶雷达与导航系统选择7/8防水插座的原因分析
概述 船舶雷达与导航系统在现代航海中扮演着至关重要的角色,它们为船舶提供准确的导航信息,确保航行的安全和效率。在这些系统中,7/8防水插座的使用尤为重要,因为它们能够在恶劣的海上环境中提供稳定的电力和信号连接。接下来&am…...

墨烯的C语言技术栈-C语言基础-006
六.常量 C语言的常量为 字面常量 const修饰的常变量 #define定义的 枚举常量 int main() { // 四个都是字面常量 30; 3.14; "w"; // 字符常量 "abc"; // const修饰的常变量 const int a 10; // 在C语言中,const修饰的a,本质是变量,但不能直…...

常用SHELL命令
在 Unix/Linux 系统中,除了基本的文件和目录操作命令外,还有许多强大的工具命令,用于文本处理、系统监控、文件操作等。以下是一些常用的 Shell 命令,特别是类似 sed 和 awk 的文本处理工具: 文本处理命令 sed - 流编…...

Python脚本:将Word文档转换为Excel文件
引言 在文档处理中,我们经常需要将Word文档中的内容转换成其他格式,如Excel,以便更好地进行数据分析和报告。针对这一需求,我编写了一个Python脚本,能够批量处理指定目录下的Word文档,将其内容结构化并转换…...

【单链表】03 设L为带头结点的单链表,编写算法实现从尾到头反向输出每个结点的值。
🕺作者: 主页 我的专栏C语言从0到1探秘C数据结构从0到1探秘Linux算法题上机准备 😘欢迎 ❤️关注 👍点赞 🙌收藏 ✍️留言 题目 设L为带头结点的单链表,编写算法实现从尾到头反向输出每个结点的值。 算法…...
鸿蒙开发设备管理:【@ohos.vibrator (振动)】
振动 说明: 开发前请熟悉鸿蒙开发指导文档:gitee.com/li-shizhen-skin/harmony-os/blob/master/README.md点击或者复制转到。 本模块首批接口从API version 8开始支持。后续版本的新增接口,采用上角标单独标记接口的起始版本。 导入模块 imp…...

【信息学奥赛】CSP-J/S初赛07 排序算法及其他算法在初赛中的考察
本专栏👉CSP-J/S初赛内容主要讲解信息学奥赛的初赛内容,包含计算机基础、初赛常考的C程序和算法以及数据结构,并收集了近年真题以作参考。 如果你想参加信息学奥赛,但之前没有太多C基础,请点击👉专栏&#…...

第N7周:seq2seq翻译实战-pytorch复现-小白版
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 理论基础 seq2seq(Sequence-to-Sequence)模型是一种用于机器翻译、文本摘要等序列转换任务的框架。它由两个主要的递归神经网络&#…...

java集合(1)
目录 一.集合概述 二. 集合体系概述 1. Collection接口 1.1 List接口 1.2 Set接口 2. Map接口 三. ArrayList 1.ArrayList常用方法 2.ArrayList遍历 2.1 for循环 2.2 增强for循环 2.3 迭代器遍历 一.集合概述 我们经常需要存储一些数据类型相同的元素,之前我们学过…...
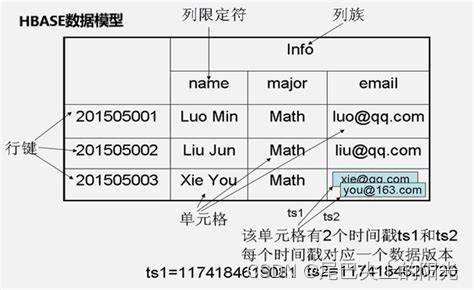
分布式数据库HBase:从零开始了解列式存储
在接触过大量的传统关系型数据库后你可能会有一些新的问题: 无法整理成表格的海量数据该如何储存? 在数据非常稀疏的情况下也必须将数据存储成关系型数据库吗? 除了关系型数据库我们是否还有别的选择以应对Web2.0时代的海量数据? 如果你也曾经想到过这些问题, 那么HBase将是…...

接口测试流程及测试点!
一、什么时候开展接口测试 1.项目处于开发阶段,前后端联调接口是否请求的通?(对应数据库增删改查)--开发自测 2.有接口需求文档,开发已完成联调(可以转测),功能测试展开之前 3.专…...
已经安装deveco-studio-4.1.3.500的基础上安装deveco-studio-3.1.0.501
目录标题 1、执行exe文件后安装即可2、双击devecostudio64_3.1.0.501.exe2.1、安装Note (注意和4.1的Note放不同目录)2.2、安装ohpm (注意和4.1版本的ohpm放不同目录)2.3、安装SDK (注意和4.1版本的SDK放不同目录) 1、执行exe文件后安装即可 2、双击devecostudio64_3.1.0.501.e…...

【C++】 解决 C++ 语言报错:Use of Uninitialized Variable
文章目录 引言 使用未初始化的变量(Use of Uninitialized Variable)是 C 编程中常见且危险的错误之一。它通常在程序试图使用尚未赋值的变量时发生,导致程序行为不可预测,可能引发运行时错误、数据损坏,甚至安全漏洞。…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
